决策树ID3新属性选择方法

王子京，刘 毓

（西安邮电大学 通信与信息工程学院，陕西 西安 710121）

0 引 言

ID3算法因简洁高效而受到广泛的关注，其选择信息增益最大的条件属性作为分裂节点，不过ID3存在多值属性偏向的问题[1]。C4.5算法利用信息增益率作为属性分裂的标准，在一定程度上避免了多值属性偏向问题[2]。然而，ID3和C4.5算法都需要计算信息增益，涉及对数运算，计算量较大。基于粗糙集[3]以及粗糙逻辑的决策方法可以灵活地处理多种决策表，适用于大数据，输出结果相对复杂。决策树一般处理多条件属性、单决策属性的决策表，输出结果较为简单，与粗糙集方法相配合，可以优势互补，避免对数运算带来的计算量以及多值属性的偏向问题。

文献[4]提出加权平均粗糙度的概念，计算每个条件属性下近似与上近似的加权比来判断该属性的分类性能。这种方法偏向于属性的分类效率。

文献[5]提出条件属性重要度的概念，将所有条件属性正域集与去掉某一条件属性后的正域集模的差值作为分裂属性的标准。这种方法偏向于属性的分类精度。然而，这两种方法均未充分考虑条件属性与决策属性之间的逻辑关系，因而由这两种方法求出的属性分类能力差别可能过小，有时不足以作为分裂属性的依据。

文献[6]引入属性协调度的概念，计算某个条件属性与决策属性的等价类与该条件属性等价类的模的比值度量该条件属性的分类能力。这个方法考虑了条件属性与决策属性的相关性，算法性能有一定的提高。

本文在属性协调度的基础上，考虑条件属性与决策属性之间的逻辑关系，提出相容度的概念，以条件属性的相容度作为分裂数据集的标准。最后，在UCI的3个公共数据集上应用本文提出的新属性选择方法。结果表明，与传统ID3算法相比，本文提出的改进算法具有更高的预测准确率。

1 ID3 算法原理

设一样本集S={S1,S2,…,Sn}，样本个数为。设D={D1,D2,…,Dm}为决策属性集，Dj（j=1,2,…,m）表示第j类属性，|Dj|表示Dj类下样本个数。则D的信息熵info(D)表示为：

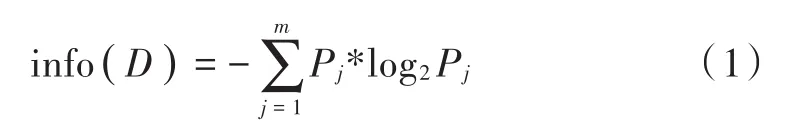
式中Pj为第j类的概率，一般用该类下样本个数与总样本个数的比值进行估计。

设A={A1,A2,…,Ak}为一个条件属性集 ，A（ii=1,2,…,k）为第i个条件属性的取值，|Ai|表示该取值下的样本个数，Aij表示Ai下的第j类，|Aij|表示该类的样本个数。那么条件属性A划分后的信息熵为：

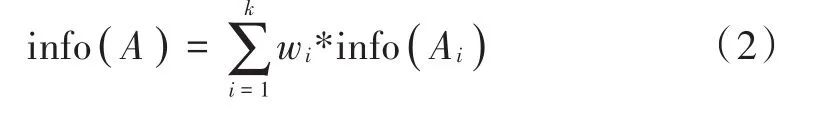
属性A划分前后的信息熵之差为信息增益，表达式为：

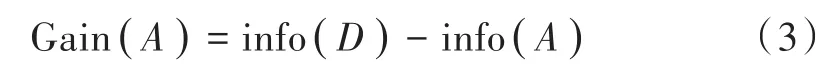
ID3算法的核心思想是分别计算每个属性划分前后数据的信息熵之差（信息增益），分裂节点时，以最大信息增益的属性为节点，即把最能有效分类的条件属性用作节点分裂，以保证每次分裂的样本最纯，生成的决策树较为简洁。经过反复迭代，直至叶子节点只有一类或所有条件属性均用作分裂节点。

2 粗糙集基本原理

对于上述运算量大和偏向选择多值属性的问题，有学者提出一种基于粗糙集的改进算法[7-8]，其核心思想是用条件属性的粗糙度作为选择分裂属性的标准，无需对数运算，减少了运算量，避免了优先选择多值属性。

2.1 信息系统

2.2 等价类与不可区分关系

在(U,R)中，R为一个等价关系，U R表示一个等价类构成的集合，即U上元素在等价关系下的分类构成的集合。设P是R的一个非空子集，那么∩P（所有等价关系的交集）也是一个等价关系，称为不可区分关系，用IND（P）表示。不可区分关系下的等价类是信息系统的最小单元。

2.3 属性协调度

在决策系统S=(U,C∪D,V,f)中，C是已知知识，可以看作变量；D是被表达的知识；等价类U/(C,D)表示条件属性集与决策属性集的交集，逻辑意义是在C已知的情况下，蕴含D的样本集合，即C→D的样本集合。它的模用|C∪D|表示，是度量C→D的逻辑关系强弱的测度，从统计学角度看，则是决策规则的频度。属性协调度[6]Con(X→D)的数学表达式如下：

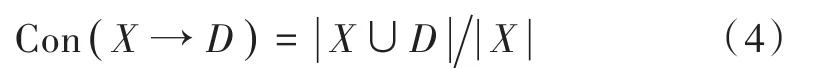
式中：X是C的非空子集；|⋅|是求模运算。

属性协调度可以表达属性的分类能力，协调度越大的属性越重要。属性协调度实际是决策表中前后件相同的集合与前件集合的模的比值。不过，属性协调度是一个宏观的统计，未能考虑各个决策规则的相容关系，在很多情况下两个条件属性的协调度差值过小，使得决策依据不够充分。实际上，决策规则中有不少是相互矛盾（不相容）的，有必要微观地考虑各个决策间的关系以提高算法性能。

3 改进算法

改进方法的主要思想是在属性协调度的基础上，考虑决策规则间的微观逻辑关系，定义一个属性相容度。用属性相容度代替原来的属性协调度作为分裂节点的标准。

3.1 主决策集与次决策集

设存在一个条件属性集C与一个决策属性集D，则中，与决策规则C→Ri矛盾的集合是依次对IND(C,D)下的集合求模，模值最大集合定义为主决策集，模值次大的集合定义为次决策集。显然，主决策集与次决策集间呈矛盾关系。对于一个条件属性而言，最坏的一种情况是主决策集与次决策集的模值相等。

3.2 属性相容度

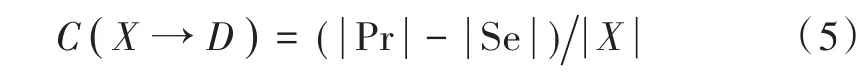
式中：X为C的非空子集；|⋅|是求模运算。由于考虑了次决策集对主决策集的影响，故式（5）为严相容度。

相容度的另一个表达式为：

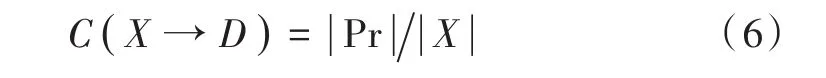
由于将次决策集舍去，不予考虑，故式（6）为宽相容度。比较两个条件属性的相容度时，若式（4）计算结果相同，可进一步用式（5）计算，保证这两个条件属性的区分度。

3.3 改进算法流程

改进算法流程如下：

1）数据初始化，将所有条件属性标记为活跃属性；

2）求出各个条件属性的主决策集与次决策集的模值；

3）用式（5）计算所有条件属性的相容度，若有两个或两个以上属性的相容度相近，继续用式（6）计算；

4）选择相容度最大的条件属性作为分裂节点分隔样本集，并将该属性去除活跃属性标记；

5）继续选择活跃属性，继续分裂样本集，直至活跃属性不存在或达到叶子节点；

6）生成决策树，剪枝。

3.4 实例分析

本文以训练样本集为例说明改进算法的步骤。训练样本集见表1。方便起见，4个条件属性用A1，A2，A3和A4表示，决策属性用D表示。易得：

则：

同理，可得：

显然，A3属性的相容度大于其他属性的相容度，因此选择A3作为分裂节点。这里A1属性有3个取值，而A3属性有2个取值，昆兰用信息熵的方法选择A1属性作为分裂节点。而本文的改进算法选择A3作为分裂节点，说明改进算法避免了多值属性的偏向问题。

4 实验及结果

4.1 数据集介绍

本文选用3个UCI公开数据集测试改进算法的性能。这3个数据集分别是：kr-vs-kp数据集、house-votes-84数据集和tic-tac-toe数据集。其中，kr-vs-kp数据集样本个数为3 196，条件属性个数为36。house-votes-84数据集样本个数为435，条件属性个数为16。tic-tac-toe数据集样本个数为958，条件属性个数为9。这3个属性集的取值均为离散值。本文所有仿真实验均在Matlab 2011软件中完成。

4.2 实验结果及分析

本文分别应用传统ID3算法与改进ID3算法生成决策树，随后用测试集测试预测准确率，结果见表2。

表2 实验结果Table 2 Experimental results

不难发现，改进算法得出的准确率从总体上优于传统ID3算法的准确率。改进的ID3算法引入粗糙集的思想，充分把握条件属性与决策属性的逻辑关系，计算属性的相容度，有效杜绝多值属性的偏向问题。实验结果符合理论预期。对于海量数据而言，传统ID3算法需计算条件属性的信息熵增益，涉及大量对数运算，而基于粗糙集的改进算法只需求出各个等价类的交集与模值。因此，改进ID3算法更适用于一般数据。

5 结 语

本文针对传统ID3算法中存在的多值属性偏向问题，提出基于粗糙集的改进方法，计算属性相容度分裂数据集。仿真实验证明，该方法具有一定的优越性。在原有粗糙集的改进思路基础上，所提方法进一步提出属性相容度，充分考虑了条件属性与决策属性之间的逻辑关系，因而具有更高的预测准确率。