邻域系统中对象变化的动态属性约简算法

向 伟

(四川文理学院智能制造学院 四川 达州 635006)

0 引 言

属性约简是数据挖掘领域中研究的热点之一，它能够在保持信息系统分类能力不变的情况下，剔除冗余的属性。粗糙集[1]作为一种智能信息处理技术，自1982年提出以来，已经在机器学习、数据挖掘、模式识别等[2-5]领域得到了广泛应用，以粗糙集为工具可以对信息系统进行有效属性约简。

目前，从实际生产、生活中获取的数据呈现多样化，使得信息系统中的数据不仅仅是离散型的，同时拥有离散型和数值型数据的混合信息系统也很常见，此类系统称为邻域信息系统。为了对邻域系统进行属性约简，李少年等[6]提出了基于邻域信息熵度量数值属性快速约简算法;何松华等[7]提出了基于邻域组合测度的属性约简方法；吴克寿等[8]提出了基于邻域关系的决策表约简算法。但是这些算法没有考虑到当信息系统中对象增加或者减少时，如何高效地对信息进行属性约简。文献[9]提出了不完备决策信息系统中的动态属性约简算法；文献[10]提出了集值信息系统中的动态属性约简算法。但是这些算法不能有效处理邻域信息系统，只适合处理静态的数据。然而，实际应用中，数据的动态变化是时有发生的，比如对于一个公司的员工考察信息表，随着新员工的加入，信息表中的对象就会增加，随着一些员工的辞职，信息表中的对象就会减少。

为了对对象变化的邻域系统进行动态属性约简，本文介绍了邻域系统中的差异度概念。当系统中的对象增加或减少时，分析了差异度的变化机制。在此基础上，提出了邻域系统中对象变化的动态属性约简算法，实验验证了所提算法的可行性与高效性。

1 相关概念

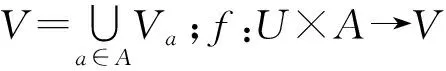
定义2设邻域信息系统NI=(U,A,V,f,δ)，属性子集B⊆C，定义B上的δ邻域关系为：

NRδ(B)={(x,y)∈U×U|DB(x,y)≤δ}

(1)

式中：DB(x,y)表示在属性子集B上对象x和y之间的距离。

为了可以处理同时有离散型和数值型的不完备邻域信息系统，本文中的距离采用文献[7]中的距离函数。设B={a1,a2,…,an}，距离度量为：

(2)

式中：1≤l≤n。

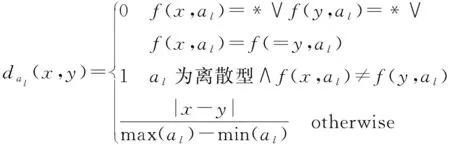
(3)

定义3设邻域信息系统NI=(U,A,V,f,δ)，∀x∈U，B上x的邻域为：

(4)

定义4设邻域信息系统NI=(U,A,V,f,δ)，对象集X⊆U关于属性子集B⊆C的上、下近似和边界域分别定义如下：

(1)X的上近似：

(2)X的下近似：

(3)X的边界域：

定义5设邻域信息系统NI=(U,A,V,f,δ)，对于B⊆C，D关于B的正域定义为：

(5)

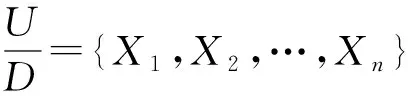
定义6设邻域信息系统NI=(U,A,V,f,δ)，对于∀B⊆C，若满足下列条件，则称B为C的一个正域属性约简。基于正域不变来定义属性约简是一个较为常见的方法[7,11-13]。

1)POSB(D)=POSC(D)；

2) ∀a∈B，满足POSB-{a}(D)≠POSC(D)。

2 邻域系统中基于差异度的属性约简

本节给出了邻域系统中差异度的概念，基于差异度提出了启发式属性约简算法。

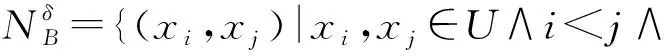
定理1给定邻域信息系统NI=(U,A,V,f,δ)，对于属性子集B⊆C,有：

(6)

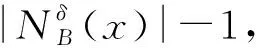
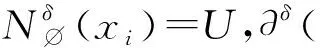
由定义7易计算出B上的差异对象集合，又由于属性集合B上的差异度等于B上的差异对象集合的大小，所以B上的差异度也较容易得到。

定义9给定邻域信息系统NI=(U,A,V,f,δ)，对于∀B⊆C,若满足下列条件，则称B为C的一个差异度属性约简。

1) ∂δ(B)=∂δ(C)；

2) ∀a∈B满足∂δ(B-{a})≠∂δ(C)。

定理2给定邻域信息系统NI=(U,A,V,f,δ)，对于∀B⊆C,B为C的一个差异度属性约简与B为C的一个正域属性约简是等价的。

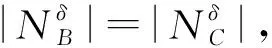
定义10给定邻域信息系统NI=(U,A,V,f,δ)，∀B⊆C，对于a∈C-B的基于差异度的属性重要度为：

SGFouter(B,a,D)=

∂(B)-∂(B-{a})=

对于a∈B的基于差异度的属性重要度为：

SGFinner(B,a,D)=

∂(B-{a})-∂(B)=

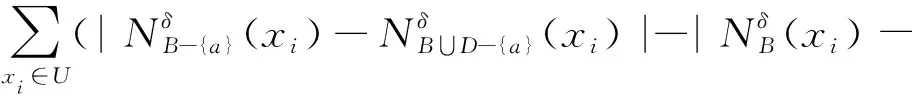
定义10可以用来对属性的重要度大小进行度量，属性重要度越大，表示此属性越重要。

根据以上关于差异度的定理与定义，本文给出基于差异度的启发式属性约简算法，见算法1。

算法1基于差异度的启发式属性约简算法(HARADD)

输入：一个邻域信息系统NI=(U,A,V,f,δ)；

输出：属性约简集合RED。

Step1初始化RED=∅；

Step2Fori=1 to |C|

IfSGFinner(ai,C,D)≠0

RED=RED∪{ai}

End If

End For

Step3while ∂(RED)≠∂(C)

对于∀aj=C-RED

计算SGFouter(aj,RED,D)，

If

SGFouter(a′,RED,D)=max{SGFouter(aj,RED,D)}，

RED=RED∪{a′}

End If

Step4输出RED。

算法时间复杂度分析：Step2的时间复杂度为O(|C|2|U|2)，Step3的时间复杂度为O(|C-RED|·|RED|·|U|2)，所以算法1的时间复杂度为O(|C|2|U|2)。

3 邻域系统中对象变化的动态属性约简

第2节提出了一个基于差异度的启发式属性约简算法，而实际应用中，信息系统中的数据常常是变化的，其中一个重要的变化就是对象的变化，包括对象的增加或者减少。本节讨论对象动态变化的邻域系统中的属性约简问题。

在算法1中，差异度是通过计算邻域得到的，对于对象变化的邻域信息系统，更高效地更新邻域是最为关键的一步。

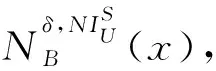
(1) 当增加对象集合△U+，有：

(2) 当减少对象集合△U-，有：

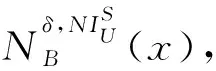
定理4说明了当邻域信息系统中的对象变化之后，更新对象邻域的过程。

定理5给定动态邻域信息系统NIS+1=(NIS,△NI)，对于∀B⊆C，差异度为：

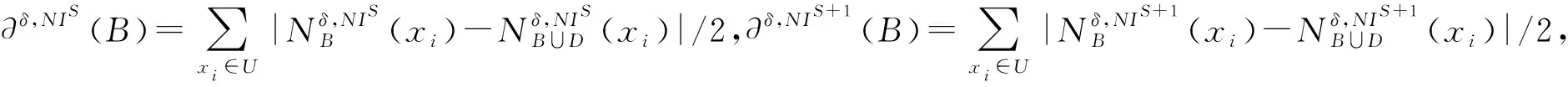
∂δ,NIS+1(B)=

定理5说明了当邻域信息系统中的对象变化之后，差异度的更新过程。

对于对象变化的动态邻域信息系统，基于以上邻域和差异度更新的机制，提出邻域信息系统中对象变化的动态属性约简算法，见算法2。

算法2邻域信息系统中对象变化的动态属性约简算法(DARAOC)

输入：动态邻域信息系统NIS+1=(NIS,△NI)，原始属性约简集为REDS，原始差异度为∂δ,NIS(C)；

输出：新的属性约简集REDS+1。

Step1初始化REDS+1=REDS；

Step2while ∂δ,NIS+1(REDS+1)≠∂δ,NIS+1(C)

对于∀ai∈C-REDS

计算SGFouter(ai,REDS+1,D)，

If

SGFouter(a′,REDS+1,D)=max{SGFouter(a,REDS+1,D)}

REDS+1=REDS+1∪{a′}，

更新∂δ,NIS+1(REDS+1)；

End If

Step3对于∀a∈REDS+1

计算SGFinner(ai,REDS+1,D)，

IfSGFinner(ai,REDS+1,D)=0

REDS+1=REDS+1-{a}，

更新∂δ,NIS+1(REDS+1)；

End If

Step4输出REDS+1。

算法时间复杂度分析：Step2的时间复杂度为O(|C-REDS+1|·|C|·|U|·|△U|)，Step3的时间复杂度为O(|REDS+1|2·|U+△U|2)，所以算法2的时间复杂度为O(|C-REDS+1|·|C|·|U|·|△U|+|REDS+1|2·|U+△U|2)。如果用算法1重新对对象变化的邻域信息系统进行属性约简，时间复杂度为O(|C|2·|U+△U|2)。显然，算法2的属性约简效率优于算法1。

4 实验结果分析

为了验证本文所提算法的可行性与高效性，将算法DARAOC与HARADD、邻域系统中正域属性约简算法(PDARA)[8]进行比较。

从UCI学习库[14]中选4个数据集进行实验，数据集的具体信息的如表1所示。本次实验用MATLAB语言实现，硬件环境为Intel处理器3.7 GHz，内存4 GB。

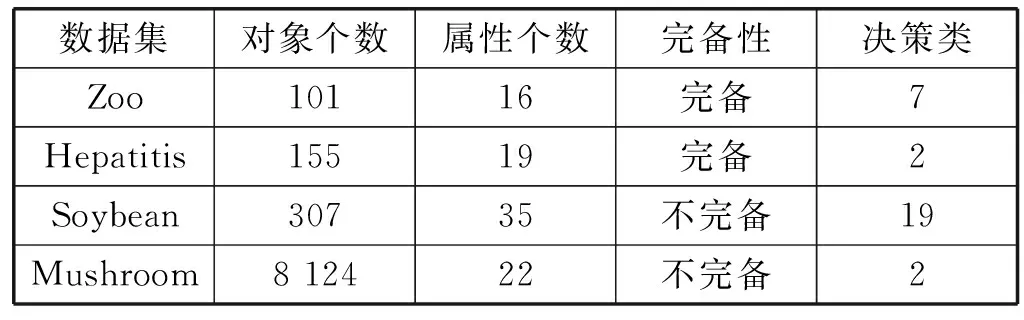
表1 UCI中的四个数据集

对于每个数据集，以20%为递增量，依次选取整个对象集合的20%、40%、60%、80%和100%的对象进行属性约简，选取邻域参数δ=0.5。实验结果如图1所示。

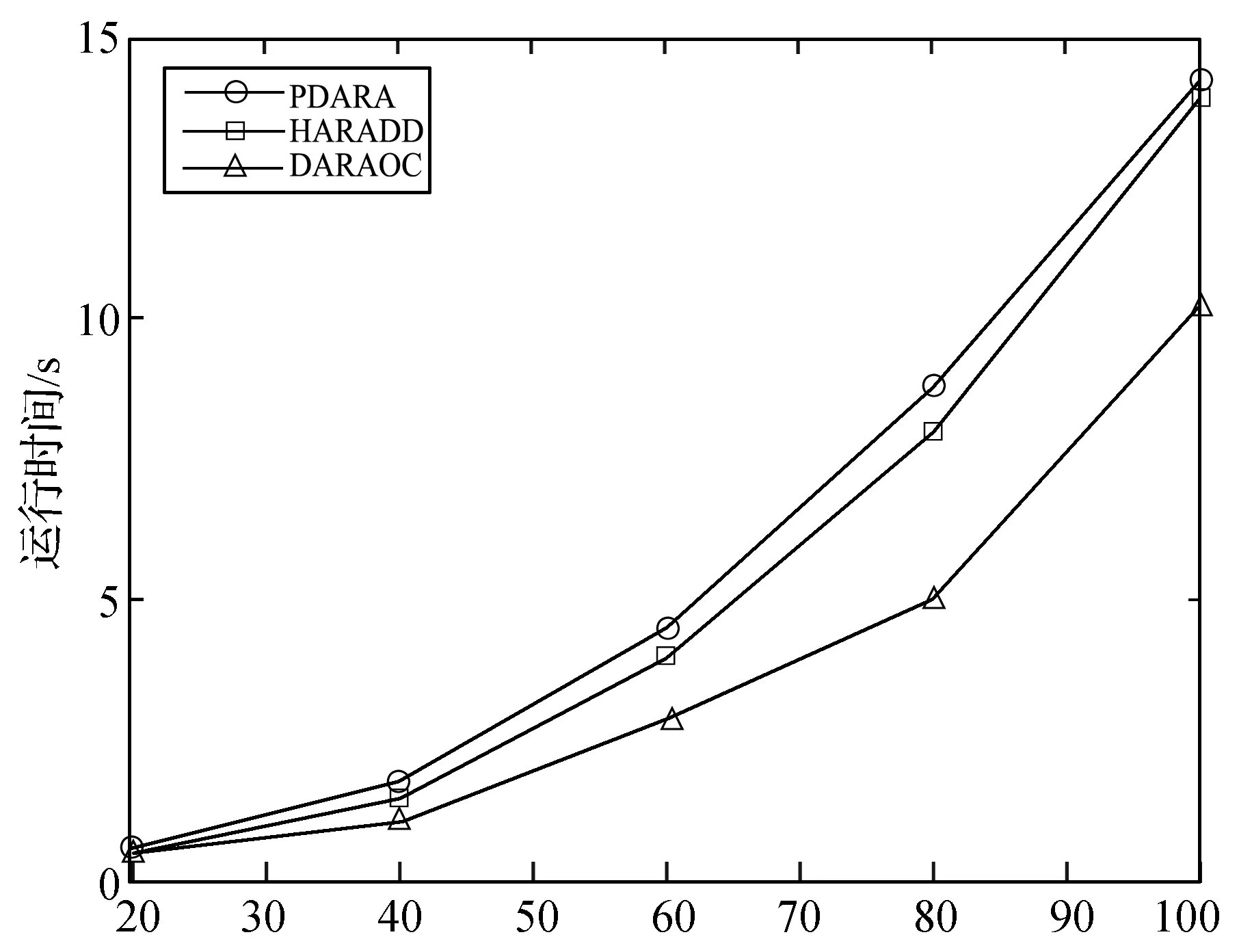
选择对象的比率/%(a) Zoo

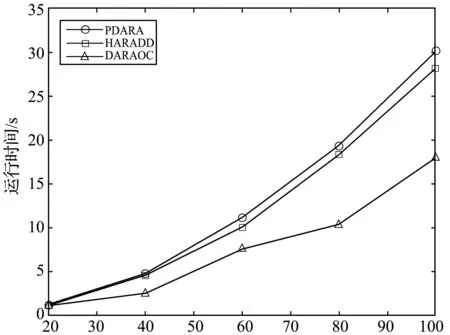
选择对象的比率/%(b) Hepatitis

选择对象的比率/%(c) Soybean

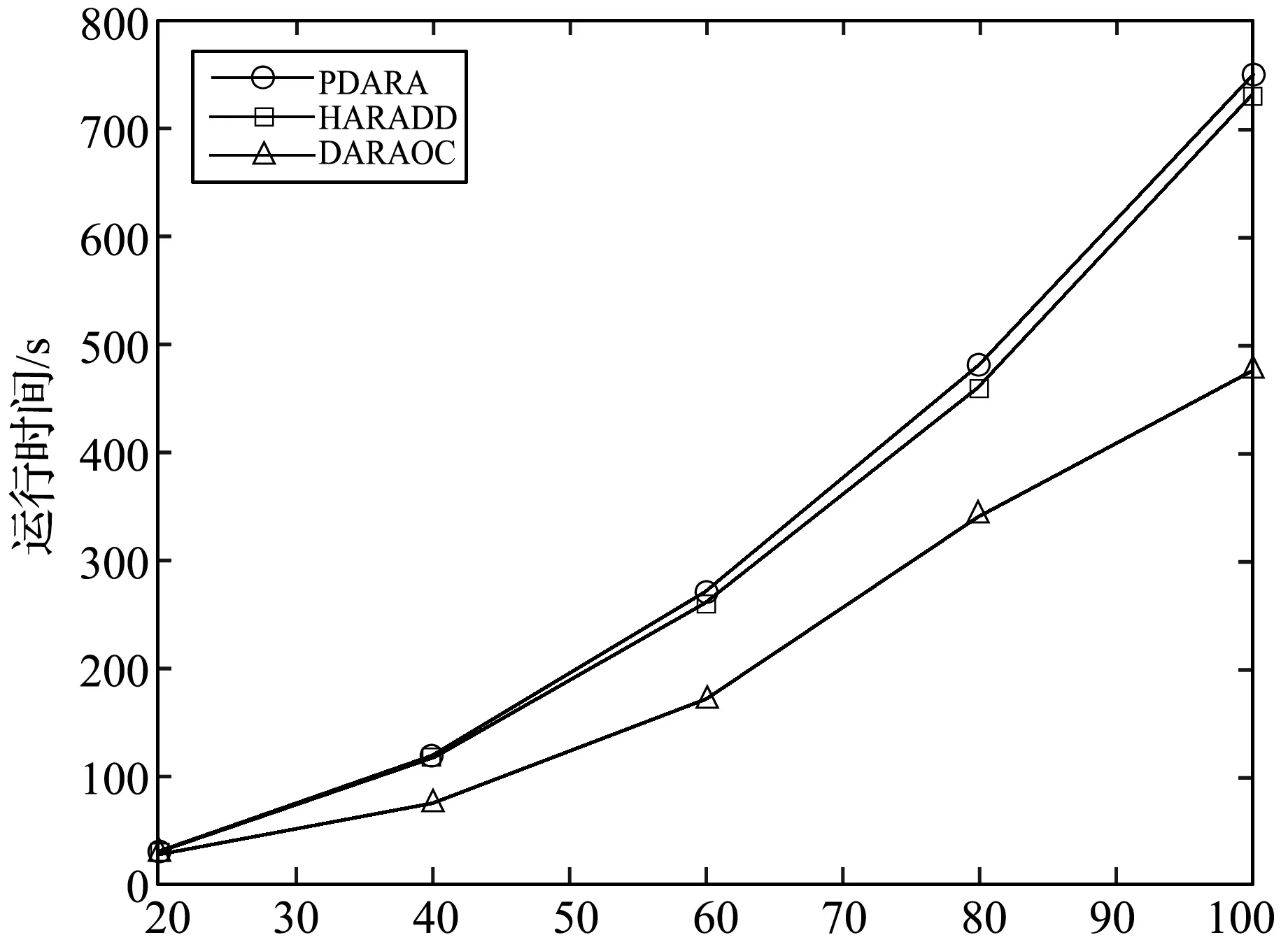
选择对象的比率/%(d) Mushroom图1 三种约简算法实验结果对比

由图1可以看出，在所有数据集上，本文算法HARADD的运行时间都低于算法PDARA，但运行时间较为接近，效率优势并不明显。这是因为两种算法都不能动态地进行属性约简，当系统中的对象动态变化时，算法PDARA基于正域不变来重新对新系统进行属性约简，算法HARADD基于差异度不变来重新对新系统进行属性约简，因此算法效率都不高。

算法DARAOC的运行时间都低于HARADD、PDARA，并且效率优势较为明显。此外，随着数据集中的对象增加，算法DARAOC相比较于HARADD、PDARA运行时间增加的较慢。可见，在处理较大数据集时，算法DARAOC效率优势更大。

5 结 语

由于现有的数据集常常同时有离散型和数值型的数据，并且可能存在数据的缺失，因此邻域信息系统成为一个研究热点。为了对邻域信息系统进行约简，本文提出了差异度的定义，并给出了基于差异度的属性约简算法。考虑到邻域信息系统中存在对象变化的情况，给出了邻域信息系统中对象变化的动态属性约简算法。该算法可以更高效地对对象变化的邻域信息系统进行属性约简。