基于NAG的BP神经网络的研究与改进

景立森 丁志刚 郑树泉 廖 威

1(上海市计算技术研究所 上海 200040)2(上海产业技术研究院 上海 201206)3(上海计算机软件技术开发中心 上海 201112)4(上海嵌入式系统应用工程技术研究中心 上海 201112)

0 引 言

近年来，随着计算机硬件和人工智能的迅速发展，涌现出丰富的机器学习算法。由文献[1]提出的对神经网络影响深远的误差反向传播算法(Back Propagation Algorithm)作为最流行的算法之一，也是应用最广泛的算法，其研究价值是不言而喻的。对于神经网络的优化，梯度下降也是最常用的优化方法之一。基于梯度下降的误差反向传播算法，在学术界和工业界都得到了很大程度的关注，对研究和改进此算法也是呈现极大的热情。

基于vanilla策略是梯度下降算法中最简单、方便的参数更新策略。参数沿着梯度变化的反方向更新，但此策略面对等高线或马鞍面时学习速度较慢。为了克服这一缺点，文献[2]提出了基于动量的更新策略[2]。在一定程度上提高了梯度下降的泛化能力和收敛速度，但是仅考虑到前一次梯度向量和当前梯度向量，没有突出当前梯度的重要性。NAG算法[3]考虑到了前梯度向量迈出一步之后的梯度变化，使得梯度下降可以具有预测性，NAG虽然比较智能，但是当前梯度动量和迈出一步之后梯度方向动量没有统一的标准，泛化能力还可以进一步优化。本文在动量更新策略和NAG的基础上，通过确定当前梯度和预测梯度呈黄金分割比例来优化，泛化能力得到了进一步的提高。

对于BP神经网络隐含层神经元的确定，以往都是凭经验确定，数目过多会过拟合，数目过少特征提取又不充分。经验主义的学者们都是基于定量的，这样也不能很好地得到较优的BP网络。

本文对于当前误差反向传播神经网络存在的两个问题，建立了基于黄金分割比的GNAG动量更新梯度策略，以及基于黄金分割比的隐含层神经元确定策略，使得BP神经网络的性能得到进一步优化。将此算法应用于手写数字识别，得到了较好的收敛速度和评估结果。

1 BP神经网络

BP神经网络是目前应用最广泛的神经网络[4]，对于经典的三层结构其拓扑结构如图1所示。

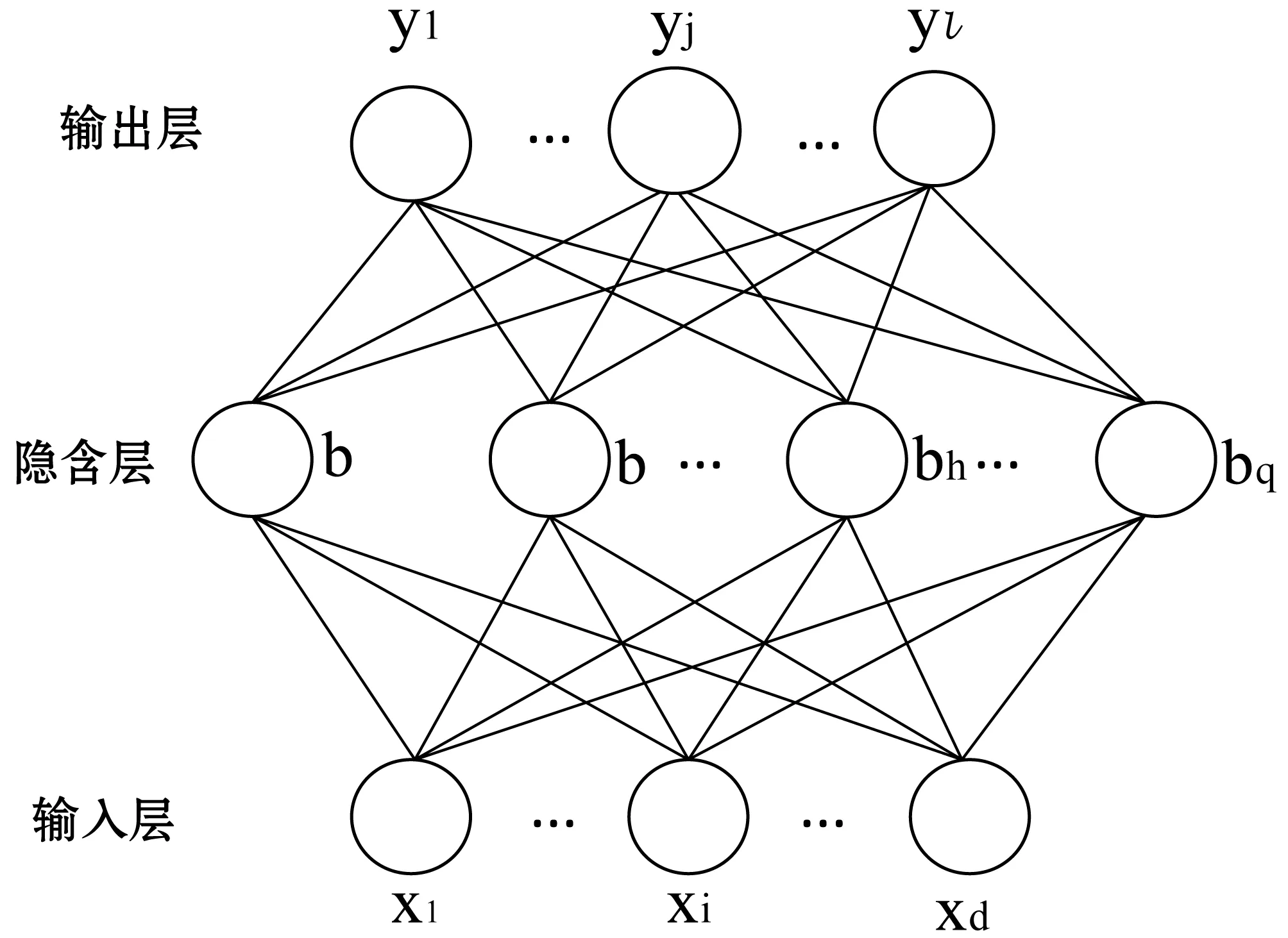
图1 BP神经网络

1.1 经典梯度下降

(1)

网络在(xk,yk)上的均方误差为：

(2)

对于图1的网络，需要确定的参数有：输入层到隐含层的d×q个权值，隐含层到输出层的q×l个权值，q个隐含层神经元的阈值，l个输出层神经元的阈值，总共有(d+l+1)q+l个参数需要确定[5]。

BP算法基于梯度下降策略，以目标的负梯度方向对参数进行优化，对式(2)的误差Ek，给定学习率η，由偏微分的性质，则有：

(3)

由βj的定义，显然可以得到:

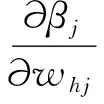
(4)

根据式(1)和式(2)，有:

(5)

将式(4)和式(5)代入式(3)，即可得到BP算法关于whj的更新公式：

Δwhj=ηgjbh

(6)

对于输出层神经元阈值有：

(7)

对于输入层和隐含层的权值，有：

(8)

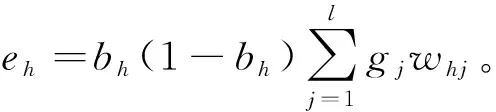
对于隐含层的阈值，有：

(9)

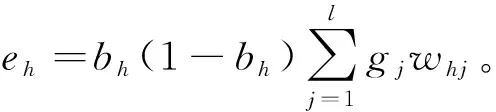
至此，根据式(6)-式(9)，BP网络中(d+l+1)q+l个参数即可更新迭代BP网络。

1.2 BP神经网络隐含层数目的确定

为了抑制欠拟合和过拟合，对于BP神经网络的隐含层的数目确定，既不能太多也不能太少[6]，之前一般根据算法工程师的经验，去做相应的确定和优化。

随着人们对BP隐含层的深入研究，找到了一种相对来说有效的确定方法。对于图1所示的BP神经网络，隐含层神经元的数目q可以用以下公式来确定[7]：

(10)

式中：d是输入层神经元的维度；l是输出层神经元的维度；a是一个取1到10之间的调节常数。但是这种确定方法对于a的确定也是凭经验来调节的，需要很多尝试，特别是对于维度比较小的BP网络，a的确定偶然因素太大。

2 BP算法改进

2.1 梯度下降算法动量更新策略

(11)

式中：w是粒子的坐标矢量。可以把式(3)看作是一种没有质量的特殊粒子的情况。

通过对比梯度下降算法的更新策略和运动物体在保守力作用下在粘性介质中运动的对比，如果牛顿第二定律可以在梯度下降算法中起到某种作用，那将是很好的更新策略。下面来阐释怎么把牛顿定律类比地用在梯度更新策略上的。为了方便，把式(11)离散化一下：

(12)

对式(12)，左右调整变形一下可得:

(13)

在物理学中，一个运动的物体具有惯性，把这个思想运用到梯度下降算法中，也就是说在梯度更新时，既在一定程度上保留先前更新的梯度方向的同时，也利用当前梯度方向做相应的调整[2]。根据式(13)可以设:

(14)

式中：

到此，使用最速梯度下降的动量更新策略和物体的运动规律有机地结合在一起，可以看出，当ε=0意味着m=0，反之亦然。

2.2 NAG动量更新策略

当使用动量更新梯度算法时，可以看成是把一个小球扔下山坡，小球积累动量，速度变得越来越快，直到达到谷底。类似地，在动量更新策略沿着梯度最大的反方向往谷底滚去，直到抵达误差函数的最低点。

对于式(14)的动量更新策略，小球从山上滚下去的时候，盲目地沿着斜率方向走，并不会得到最优解。我们希望有一个智能的小球，可以知道自己要滚到哪里去，在下坡的过程中加速，在稍微有上坡的趋势的时候减速。此策略不但加快了收敛速度，同时可以抑制摇摆[8]。NAG是一种能够给动量这种预测能力的一种算法[9]。对于普通的动量更新策略如图2所示。

图2 普通动量更新策略

ε为更新先前一次梯度方向上的动量学习率，p为更新当前点梯度方向上的动量学习率。观察式(14)可以把参数迭代分为两步来走，如图3所示。

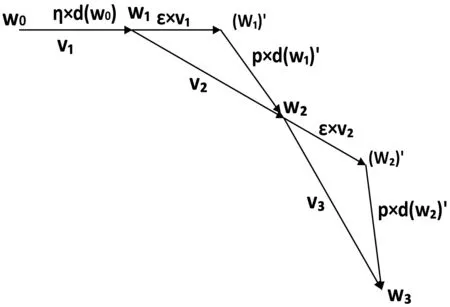
图3 NAG动量更新策略

先沿着先前的更新方向继续前进ε×vi-1,到达点(wi-1)′,再沿着(wi-1)′的梯度方向前进p×d((wi-1)′),到达wi，此方法即为NAG。由于在更新动量之前，在点(wi-1)′做梯度方向的调整，属于超前预测，这种做法是有一定的“向前看”的优势[10]，适应性比较好。

2.3 黄金分割比隐含层BP神经网络

黄金分割比是把一条线段分割为两部分，使其中一部分与全长之比等于另一部分与这部分之比，如图4所示。

图4 黄金分割比线段

黄金分割比等式：

(15)

黄金分割具有严格的比例性、艺术性、和谐性，蕴藏着丰富的美学价值。由于按此比例设计的造型十分美丽，因此称为黄金分割比，也成为中外比。这个数值的作用不仅仅体现在诸如绘画、雕塑、音乐建筑等艺术领域，而且在管理、工程设计也有着不可忽视的作用。

本文把这个完美的比例，用在神经网络隐含层神经元的数目确定和NAG动量更新中。

对于BP神经网络的隐含层的数目，过多过少都不合适，会呈现不同的欠拟合或过拟合结果，但是有一点是很明确的，即总的来说，隐含层神经元的数目肯定要在某种程度上比输入层和输出层神经元多，至于多多少，一般都是根据项目经验去尝试从而确定合适的数目。即使用式(10)来确定，a也是凭经验来调节的，需要很多尝试，偶然因素也比较大。

因此我们引入基于黄金分割比的隐含层的确定方法。对于图1所示的BP网络，令:

(16)

根据式(16)，求输入层和输出层确定的隐含层的平均，令隐含层神经元的个数为:

(17)

基于式(17)所确定的隐含层神经元数目，蕴藏着丰富的美学，能有效规避经验主义，又能很好地提取数据特征，达到很好的特征提取和数据转换工作，泛化能力进一步提高。

2.4 黄金分割比NAG动量更新策略

对于NAG算法，先沿着先前的更新方向继续前进ε×vi-1,到达点(wi-1)′,再沿着(wi-1)′的梯度方向前进p×d((wi-1)′),到达wi，故有:

(18)

动量首先计算当前梯度，接着沿着梯度负方向迈出一大步，计算梯度值，然后做修正。这个具有预见性的更新防止前进得太快，同时增强了算法的响应能力。和普通动量更新策略作对比，如图5所示。

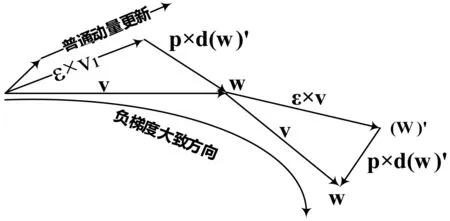
图5 NAG动量和普通动量对比图

虽然NAG有前瞻性，也有很好的预测性，收敛速度比较快，但是对于学习率ε和p，还是凭经验主义来人为设定的，泛化能力弱。通常情况下需要多次运行模型才能预估比较合适的学习率，偶然因素太大。再次引入黄金分割比，令：

(19)

称满足式(19)的NAG动量为黄金NAG动量算法，记为GNAG。由于原来需要两个学习率的确定，现在让其比值符合黄金分割比，有效地利用黄金分割的自然美学，融合到工程应用中。当前梯度负方向与下一步梯度负方向不一致时，两个动量叠加会得到有效抑制和调整，当两个动量方向大致一致时，二者叠加使得迈出一大步的学习步长。因此不但可以泛化学习算法，还可动态调整学习率，接下来利用实验来验证其有效性。

3 应用实例

3.1 实验验证

MNIST数据集是目前测试神经网络最流行的数据集之一，相对于N维奇偶问题[11]更具有代表性。采用MNIST数据集，来识别0～9的10个手写数字，图片大小是28×28，故输入维度是784的变量，输出维度是10，利用式(17)，故隐含层神经元数目为：

利用google的tensorflow开源框架来实现只含有一个隐含层的神经网络，设计并实现NAG的两个动量向量大小之比为黄金分割比，从而达到构建成GNAG的BP神经网络，利用matplotlib来可视化显示数据分析结果。构建的神经网络如图6所示。

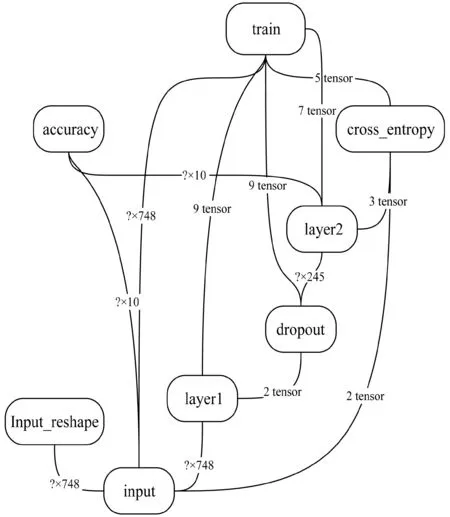
图6 GNAG-BP神经网络

3.2 结果分析

智能的NAG算法可用性已很高，而GNAG的性能比NAG更好，两者在精确度的对比如图7所示。

图7 NAG和GNAG精确度对比

由图7可知，GNAG的精确度更高，收敛速度更快，误差平均损失函数更小，故学习能力更好，泛化能力更强。

对于GNAG优化算法的精确度和交叉熵代价函数分别如图8和图9所示。

图9 GNAG损失函数

根据图8和图9，可以看出，训练的精度和误差都很陡峭，说明GNAG的学习速度极快，GNAG训练结果围绕预测结果上下浮动，基本上预测结果在训练集的中心部位，没有出现过拟合或梯度消失等现象。虽然只是用的简单的三层黄金分割比例的BP神经网络，可是对于MNIST数据集我们的正确率已经达到了97.55%，比人眼识别率还要高，可见黄金比例运用到BP网络中效果特别好。

4 结 语

本文在基于NAG算法的基础上，引入了黄金分割比，有机地结合了自然美学和工程应用，在泛化能力和收敛速度上，都得到了一定程度的提高。应用实例表明，基于黄金分割比梯度动量更新策略的BP神经网络误差更小，收敛速度更快，因此泛化能力更强。对于别的数据集，有待进一步研究和实验。