K近邻分类指导的区域迭代图割算法研究

管 建 王亚娟 王立功

(苏州大学医学部放射医学与防护学院 江苏 苏州 215123)

0 引 言

图像分割的原理是根据一定的相似性准则将图像划分成多个具有独特性质区域的过程,各区域内具有相同或相似的性质，从而达到在复杂的背景环境中把感兴趣的目标区域提取出来的目的。近十余年来，自动化图像分割在许多领域得到了广泛研究，如自然图像分割[1]、医学图像分割[2]等，但在内容复杂的图像上应用仍然存在很大的问题。理想的分割通常需要在分割过程中增加用户指导信息来获取目标，减少自动化分割带来的歧义性，因此，交互式的分割方法具有更强的实用性。

由Boykov等[3]在2001年首次提出的图割(Graph cuts)模型是目前研究和应用最为广泛的交互式图像分割方法之一。它解决了全局优化框架中的分割问题，并为广泛的能量函数提供了全局最优解决方案。传统的Graph cuts算法使用最大流算法[4-6]实施计算，将像素视为节点来构建Graph cuts模型。最坏情况下的运行时间复杂度为O(mn2|C|)，其中m、n、C分别表示边的数目、节点的数目和图中最小割的权值，所以传统Graph cuts会严重增加算法的时间成本。本文为了减少Graph cuts算法的计算时间，在原始图像上使用均值偏移(Meanshift)算法作为初始分割[7]，将原始图像分成多块同质区域，同时将这些同质区域作为加权图的节点(超像素)来构建Graph cuts模型，进行图像分割。Lazy snapping[8]算法也通过类似方法降低Graph cuts的运行成本，但其预分割算法使用的是基于灰度梯度信息的分水岭变换,忽略了彩色图像所包含的丰富信息,预分割区域的一致性不够强, 而且分水岭算法的过分割现象严重，影响后续Graph cuts的分割性能和计算效率。许多研究改进算法来降低分水岭算法的过分割现象，如应用改进的中值滤波算法对图像进行适当的降噪，较好地解决了分水岭算法中过度分割的问题，同时又降低了Graph cuts的时间复杂度[9]。另外, Lazy snapping采用K-means 方法, 这种算法通过最小化均值的方差函数来实现聚类, 而并非最大似然估计,对初始聚类中心严重敏感, 聚类效果不够理想。本文中将提出的分割方法与Lazy snapping就预分割和最终分割的效果做分析比较。

由于图像信息存在不确定性,难以获得精确的分割结果。为解决图像分割中的不确定性问题，张喆等[10]将证据理论与马尔可夫随机场相结合, 以证据距离描述相邻像素间的标号关系,利用条件迭代模型ICM(Iterated conditional mode)算法进行优化，获得较好的图像分割算法。Peng等[12]则结合ICM和最大后验估计MAP(Maximum a posteriori estimation)，使用迭代区域合并方案来扩展Graph cuts算法，渐进式地进行分割而不是一次性分割整幅图像。该算法从用户选定的种子区域开始迭代建立传播子图，子图包括已标记的超像素点和相邻的未标记超像素点。在子图上使用Graph cuts算法根据已标记的超像素点标定未标记的超像素点，并将标定完的超像素点归入已标记的超像素点集中，来进行下次迭代子图标定过程，直至所有超像素点都获得标签。但是，ICM算法受标签初始化影响很大，后续迭代中会放大先前迭代分割中的错误[13]。而Graph cuts算法也不能达到完全精确分割，每次迭代中如果将所有新标记的超像素点加入已标记的点集，那么错误标记的超像素点会在后续的迭代分割中不断放大错误，造成不可估量的后果。本文采用KNN半监督分类器，通过自训练的方式迭代训练标签数据集，并对每次局部Graph cuts模型产生的新种子区域进行置信度评估，提取高置信度的种子区域指导下轮分割。

1 图割算法分析

图像分割问题是对图像中各像素进行标签的过程，即给定一个标定场L和一个位域集合D(如图像像素或者超像素点)，我们的目标是给每个位域i∈D分配一个标签αi∈L。Boykov和Jolly提出的Graph cuts模型[3]，就是构造一个马尔可夫随机场能量泛函, 将二元标签分配的全局最优化问题转化为对相应S-T加权图的最大流/最小割问题。标签集合α={0,1}，其中0表示背景，1表示目标，标记结果称为标号场L={α1,α2,…,αi,…}(i∈D)。图1描述了这类S-T图的分割过程。

图1 图割算法分割图像流程

马尔可夫随机场能量泛函如下：

(1)

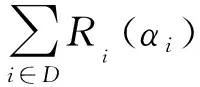
Ri(1)=-lnPr(αi|′obj′)

(2)

Ri(0)=-lnPr(αi|′bkg′)

(3)

当超像素点i更倾向于被分为目标时，Pr(αi|′obj′)大于Pr(αi|′bkg′)，将i分给目标的惩罚比分给背景的惩罚小，即Ri(1)小于Ri(0)。当所有超像素点都被正确分配标签，区域项被最小化。式(1)中的边界项根据以下的等式定义[4]。

Bij(αi,αj)=ω[i,j]·δ(αi,αj)

(4)

式中：i、j为邻近的超像素点，δ(αi,αj)定义为：

(5)

ω[i,j]定义为：

(6)

式中：Ii和Ij表示超像素点i和j的强度值，对于灰色图像使用灰度值表示强度，彩色模型使用RGB向量Ii和Ij表示强度；σ表示邻近超像素点间的强度变化程度，当两超像素点强度接近时，相应的能量惩罚很高；dist(i,j)表示两个超像素点间的距离。Boykov等[4]详细描述了最小能量问题，S-T加权图中的权重值定义如下：

(7)

在S-T图中，S为源极点，T为汇极点，当超像素点的强度倾向于归为目标对象时，其与S节点之间的权重将大于像素与T节点之间的权重，这意味着切割更可能发生在权重更小处。对于相邻的像素，当它们的强度非常相似时，权重非常大，不可能被切割分离。因此，当从S-T图中实现最小切割时，切割的位置接近物体边界，同时此时能量函数值也最小。

2 K近邻分类指导的区域迭代图割算法

图割算法为图像分割提供全局最优解决方案，然而，对于复杂图像，图割算法难以一次性精确地分割整个图像。Besag[11]提出的ICM是一种确定性算法，它使用贪婪策略，通过迭代局部最大化的方法来逼近马尔可夫随机场(MRF)的最大联合概率。采用ICM的策略，本文首先采用均值偏移(Meanshift)算法预分割图像，将分割区域作为超像素点构建S-T加权图。根据用户标记种子点建立子图，在子图上求能量函数最小值，并以此局部最小能量所对应的标号场作为新的种子点，迭代扩展子图直到达到整个图。

像ICM算法一样，这种迭代图割算法受初始化标签影响很大，如果每次迭代存在错误的初始化标签，后续迭代中初始标号场的错误将在图像分割过程中被放大。另外，尽管图割算法相较于自动分割算法，拥有用户交互信息作为分割的硬性约束，能够大大提高分割的准确性和鲁棒性，更能产生令人满意的分割结果，但仍存在错误分割的可能。所以直接将每次局部迭代分割结果作为初始信息指导下次迭代分割的方法并不是很合理，有可能影响整个分割算法的准确性。

本文提出算法的大致流程如图2所示。为了解决上述问题，该算法在每次迭代分割中使用KNN算法对本次局部分割中未标记的区域进行分类标记，以超像素点的颜色空间信息和位置空间信息为特征向量，给予局部Graph cuts算法的标记结果置信度评估。另外针对实际交互式图像分割标签分类中有标签的数据少而未标记的数据多的情况，使用自训练(self-training)半监督学习方法[14]，选择高置信度标记结果，迭代训练KNN分类器。从迭代训练中挑选出最合适的KNN分类器，将其训练集数据及对应标签作为到下次区域图割算法的种子点，更新图割算法的目标/背景模型。

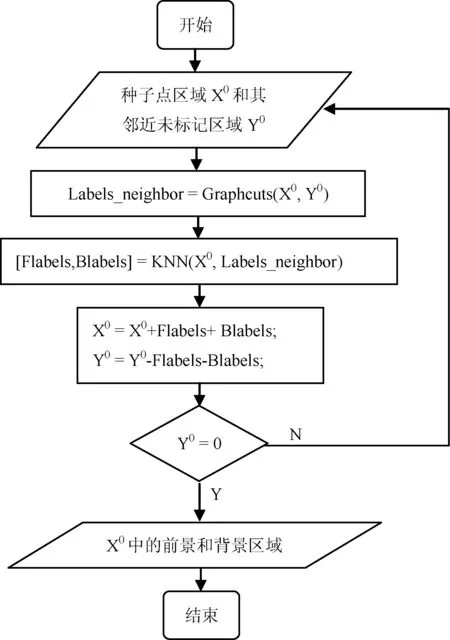
图2 本文算法的流程图

2.1 图像预处理

在Graph cuts算法中，图像分割直接在像素上进行，在S-T加权图中将每个像素作为节点计算，计算的成本很高。另外，分割结果不平滑，特别是边缘处。在Wu和Leahy工作中提出的最小割对小的孤立节点集进行的分割存在偏倚[15]。许多其他的目标函数，如平均割[16]、归一化割[17]、比率割[18]等采用新的分割标准来解决这个问题。

Lazy snapping算法[8]用分水岭变换进行预分割，首先将图像分成许多小的同质区域代替传统Graph cuts算法中的像素点，作为节点构建加权图，并以此优化加速Graph cuts过程，更好地保存目标边界。但分水岭算法对噪声非常敏感，会导致严重的超分割现象。基于预分割的Graph cuts分割模型中，准确的初始区域分割对后续的分割性能起到至关重要的作用。为减轻分水岭算法噪声的影响，本文采用均值漂移算法处理图像的预分割。根据文献[19]中的方法，在三维的LUV彩色空间和二维的位置坐标所组成的五维特征空间上进行分析，f(x)为五维特征空间上的概率密度函数，其梯度估计为：

▽f(x)∝(avgxi∈Wh,x[xi]-x)

(8)

式中：avg表示平均，Wh,x表示以x为中心并以h={hs,hr}为带宽的五维超球体，hs和hr分别表示位置空间和彩色空间的带宽。对原图像的每个像素使用梯度上升法，通过在特征空间中反复迭代寻找概率密度的极大值，再按照区域邻接图和彩色带宽进行递归合并。这种计算方式耗时较多，但相较于分水岭算法，均值漂移算法产生更少的过分割，且能提供更好的边界保存，在后续的超像素点分割中能够降低计算成本以及提高分割性能。本文预分割实验中hs=10、hr=15。

2.2 区域迭代图割算法模型建立

文献[12]建立了一种区域迭代Graph cuts模型。将图像进行如2.1节所述的预分割，分割后的图像表示为G=V,E，V是相应预分割图像超像素点的集合，E是连接相邻超像素点边的集合。由初始用户标定的种子点开始建立子图，包含种子点及其相邻超像素点，子图形式为G′=V′,E′，其中V′⊆V，E′⊆E。图像分割问题要求的是满足最大后验概率的对每个超像素点的分类标记，即第1节中的标号场L。局部分割过程中必须遵循马尔可夫性，在相邻位置上标签取值已知的条件下，标定过程只取决于相邻的标签，即P(αi|αD-{i})=P(αi|αNi)(i∈D)，Ni是i的邻近系统。在MAP-MRF框架下通过最大化条件概率P(αi|di,αD-{i})获取每个标签αi。

(9)

当d给定时，P(d)是一个标准化常量，所以:

P(αi|di,αD-{i})∝P(di|αi)·P(αi|αNi)

(10)

而后验概率满足:

P(αi|di,αD-{i})∝e-U(αi|di,αNi)

(11)

U(αi|di,αNi)为后验能量，结合式(10)和式(11)可得：

U(αi|di,αNi)=U(di|αi)+U(αi|αNi)

(12)

(13)

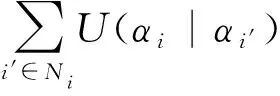
αk+1=argminαU(α|d,αk)

(14)

αk+1为第k+1次迭代中标定区域的标签，该迭代过程不断标记新的未标记超像素点，直至整幅图像被全部标记。具体算法流程见算法1。

算法1区域迭代图割算法

输入：

原始图像的预分割图像；

2.3.3 精密度试验 取“2.2.1”项下对照品溶液适量，分别加甲醇制成低、中、高质量浓度（3.84、7.68、15.36 μg/mL）对照品溶液，以甲醇为空白，于322 nm波长处测定吸光度，连续测定6次。结果，米索硝唑吸光度的RSD分别为0.93%、0.62%、0.48%（n＝6），表明仪器精密度良好。

种子点区域X0=Ro∪Rb；

种子点的邻近未标记区域Y0。

输出：图像分割结果。

1.根据标记的种子区域构建前景和背景模型；

2.建立子图G′=〈V′,E′〉，其中V′包括种子点区域X0和Y0；

3.使用图割算法求出子图G′中的最大流/最小割，给予邻近未分割超像素点分割标签；

4.根据表2中算法评估步骤3中的标签，选择具有高置信度标签的超像素点加入对应的种子点集合，更新前景和背景模型；

5.返回步骤2，直至整幅图像中没有未标记的超像素点；

6.返回最终的分割结果；

while 1

Labels_neighbor = Graphcuts(X0, Y0);

//图割算法获取邻近未标记区域标签

[Flabels,Blabels] = KNN(X0, Labels_neighbor);

//KNN分类器自训练过程算法，实现算法见表2

X0= X0+Flabels+ Blabels;

Y0= Y0-Flabels-Blabels;

if Y0= 0

break;

end

F = F+ Flabels;

B = B+ Blabels;

//F为分割的前景区域，B为分割的背景区域

end

//迭代局部图割算法

Labels_neighbor = Graphcuts(X0, Y0)

{

for i = 1:numel(Y0)

U(i) = A(i)+T(i);

//U为所求后验能量

end

[Umin,labels_new] = min(U,[],2);

labels_neighbor = [neighbors,labels_new];

//最低能量时邻近未标记区域的分配标签

}

2.3 自训练K近邻算法评估分割标签

任何分割算法都不能保证准确无误地分割性能，本文方法采用的ICM模型，将每次局部分割结果作为指导信息，迭代入下次局部分割。这就有可能将之前迭代分割中的错误在后续分割中不断放大，进而影响整个算法分割的准确性。

为此，本文中训练一个KNN分类器，使用超像素点的颜色空间信息和位置空间信息作为特征向量训练分类器。随后对每次区域迭代图割中的邻近未标记区域进行分类，并根据分类结果给予本次局部图割标记结果相应的置信度。选择拥有高置信度标签的超像素点，作为到下次分割的种子点，更新图割的目标前景/背景模型。

但由于KNN算法不能直接处理大量含有无标记数据的数据集，根据半监督分类学习的定义及文献[20]，本文采用自训练的学习算法把未标记的数据逐步分类，并将分类好的数据加到已标记数据集中去，扩大训练样本集，同时了缩小待测样本集，继续训练KNN分类器。根据分类器每次置信度评估结果计算平均置信度，训练器不断迭代直到得到最适合所分割图像的分类器，以此减少局部分割中产生的错误，提高迭代图割模型的分割性能。KNN分类器的自训练算法见算法2。

算法2KNN分类器的自训练过程算法

输入：

种子点区域X0=Ro∪Rb及相应的标签FS；

种子点的邻近未标记区域Y0；

分类器迭代训练次数T；

获取置信区域比例s；

输出：FS′

for iter = 1:T

mdl =ClassificationKNN.fit(X0,FS,′NumNeighbors′,3);

//训练KNN分类器

[label_pred,score] = predict(mdl,Y0);

//预测邻近未标记区域的分类标签

Conf = zeros(size(Y0),3);

Conf(:,1) = FS(:,1);

for i = 1:size(Y0)

if FS(i) ～= label_pred(i,1)

Conf(i,2) = 0;

elseif (FS(i,2) == label_pred(i,1))&&(label_pred(i,1)==0)

Conf(i,2) = score(i,1);

Conf(i,3) = 0;

else

Conf(i,2) = score(i,2);

Conf(i,3) = 1;

end

end

//使用KNN分类器评估图割分割标签置信度

PU = sortrows(Conf,-2);

//按置信度从高到低排序

S = ceil(size(Conf,1)*s);

PU = PU(1:S,:);

AvgConf(iter) = mean(PU(:,2),1);

//计算平均置信度

end

[AvgConf_MAX,index_MAX] = max(AvgConf,[],1);

//选择平均置信度最高的分类器的分类结果FS’

如算法2所描述，自训练学习方法同时在有类别标签数据集和无类别标签数据集上进行特征选择。首先，该算法在有类别标签数据集上进行特征选择，产生初始候选特征子集。然后在该特征子集上用有类别标签数据集训练一个带置信度输出的KNN分类器C。接着用C对无类别标签数据集上的数据进行分类预测，从而获得其类别标签，从中选择出置信度从高到低的占比s的数据，加入到原始训练集中形成一个新的训练集，迭代训练分类器。最终选择平均置信度最高的分类器作为最合适的KNN分类器，其预测标签作为新的分割种子点，进而更新局部图割算法中的目标前景/背景模型。通过实验，本文中s取0.5，训练的KNN分类器的K值取3。

图3展示了本文提出的区域图割算法在KNN分类器指导下分割图像的过程。通过用户输入种子点，分割种子点邻近区域，分配相应的对象和背景标签，并将新分割的区域作为新的种子点，更新图割算法的前景/背景模型。并且在新的前景/背景模型下分割相邻未标记区域，迭代上述过程，直至将整幅图像完全分割开，从而获得我们所期望的目标区域。图3中，(a)为用户在原始图像中标记的种子点，(b)-(j)为分割过程中的迭代分割结果。子图中每次迭代新分割区域以红色表示，背景区域以蓝色表示(颜色以灰度表示)。(k)则展示了目标对象的最终分割结果。

图3 迭代分割过程

3 实验与结果分析

本节主要展示本文提出的算法与Lazying Snapping算法图像分割实验结果的比较，并且进行定量评估的对比分析。另外，还将提出的算法在使用KNN分类器评估置信度和不使用KNN分类器评估置信度两种情况下的分割结果进行比对，探讨KNN分类器对本文所提出算法的影响。

本文实验平台为Intel Core i5-4460 CPU 3.20 GHz的CPU和4 GB的内存，实验使用MATLAB R2017a对Berkeley图像数据库中的50幅基准彩色图像进行测试，其中10张具有简单背景内容，其余图像具有相对复杂的背景内容。这些实验图像的大小分辨率有两种，分别为321×481(像素)和481×321(像素)。数据库中每张图像都有人为标记的目标-背景分布作为参考标准。

本文中的位置空间带宽hs和hr两个参数越大，分割的整体性越好，分割产生的区域数越小，分割结果越平滑，但对弱边界的识别能力越弱。反之，这两个参数越小，分割精细度越高，对弱边界的识别能力越强，但分割所产生的过分割现象越严重，为了控制分割质量，经过预分割实验效果比较，取hs=10、hr=15。

自训练过程中，KNN分类器选择的K值小，分类器的近似误差会减小，但估计误差会增大，容易发生过拟合；相反，K值大，近似误差会增大，估计误差会减小，从而有可能忽略训练集中的有用信息。这里近似误差指的是目标点对于其原样本点的可信度，也就是说，K值越小，与目标点邻近的点的标签对于其目标点的影响也就越大，其标签的一致性就越高。估计误差是原模型本身的真实性，即该模型所表现出的分类特性，是否为真实的分类特性，噪点影响、错误数据或者本身分布不是很好的数据，都会影响估计误差。如果K值比较大，那么以上缺陷就会尽可能被平均，从而减小对最终结果的影响。经过实验比较，本文中取K=3。

3.1 与Lazying Snapping算法分割效果比较

本节中将提出的算法与Lazying Snapping算法的分割效果作对比，图4中包括背景简单的图像((a)、(b))和背景相对复杂的图像((c)-(e))。图4中第一列为原始图像上用户种子点信息，第二列为Lazying Snapping算法的分割结果，第三列为本文所提出算法的分割结果。由图可知，给定相同数量的种子点，提出的方法较Lazying Snapping算法能取得更好的分割结果，分割效果也更符合人们的主观需求。

图4 Lazying Snapping算法和担出算法的图像分割效果

Lazying Snapping算法使用图割算法分割整个图像，需要人工交互信息指导，特别是对于背景相对复杂的图像，图像中很多未标记的背景区域可能会对图像分割优化产生不可预测的负面影响，往往需要更多用户标记的种子点，才能获得令人满意的分割结果。而本文中提出的算法通过在局部子图使用图割算法分割，子图显著降低图像中背景内容的复杂度，并阻挡远离标记区域的未知区域，降低背景干扰。因此如图4中五组对比图所示，在相同的用户交互量下本文中提出的算法可以获得更好的分割结果。

3.2 与无KNN分类指导的迭代图割算法分割效果比较

本节中对比的两种算法在预分割和迭代分割的方法都是一样的，差别在于是否使用自训练的KNN分类器对每次局部图割分割结果进行评估。图5展示了对比实验结果,其中：第一列为原始图像上用户种子点信息；第二列为无KNN分类指导信息的局部迭代算法的分割结果；第三列为本文所提出算法的分割结果。有KNN分类指导的局部迭代图割算法较无KNN分类指导的算法能取得更好的分割结果。

图5 无KNN分类器指导的局部迭代图割算法和本文算法的图像分割效果

根据KNN分类器基于每次局部区域分割的结果标签置信度，并用置信度信息指导下次迭代的种子点选取，可以减少局部分割中产生错误标定的可能性，避免形成的分割错误在后续迭代步进过程中被放大，进而提升分割性能和鲁棒性。

3.3 计算时间

表1显示了前文所对比的三种算法在图割算法阶段的计算时间比较。因为Lazying Snapping算法采用的是分水岭算法进行预分割，而本文提出的算法采用Meanshift算法进行预分割，直接比较两种算法的总计算时间不是很合理，所以我们对比了不同算法在图割算法阶段的计算时间。

表1 图割算法阶段的计算时间比较

续表1

本文提出的方法在时间上消耗是Lazy snapping算法的20倍左右，是未使用KNN分类器指导的1.8倍左右。但Lazy snapping算法要达到理想的分割效果，往往需要进行多次交互，每次交互都需要给予新的交互信息，所以本文方法在实际图像分割应用中具有更强的实用性。

3.4 定量评估

分割定量评估是通过与数据库参考标准分割对比，分割质量四个参数来度量，分别是TPF、FPF、TNF和FNF,定义如下：

(15)

(16)

(17)

(18)

表2是上述三种方法对50幅基准图像分割结果定量评估的平均水平。比较表中的TPF、FPF、TNF、FNF值可以看出，有KNN指导的区域迭代图割算法可以获得最佳的TPF、FPF、TNF、FNF值，较另外两种分割算法拥有更好的准确性。

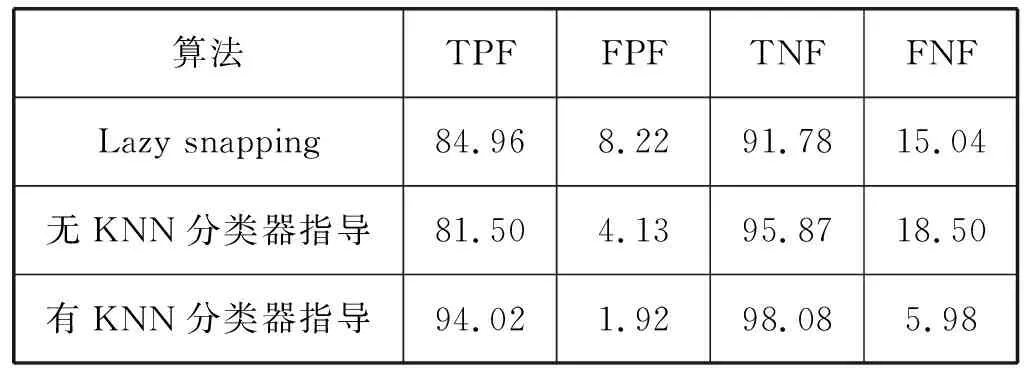
表2 数据库50幅基准图像分割结果的定量评估 %

表3是三种算法对图4中5幅图像分割的定量评估，为了直观展现算法定量评估值的对比，图6为三种算法在5幅实验图像中定量评估值的折线图。

表3 三种算法对五组图像分割结果的定量评估 %

图6 三种算法定量评估值对比

结合表2和表3分割算法定量评估数据，Lazying snapping算法虽然有些情况下也能产生不错的分割，但对初始用户交互需求较大，特别对于背景复杂的图像，其鲁棒性低于本文提出的算法；而不使用KNN分类器指导分割的算法虽然对鲁棒性没有明显影响，但其准确性不如使用KNN分类器指导分割的算法。

4 结 语

本文基于超像素构建Graph cuts加权图和局部迭代的Graph cuts模型，使用自训练KNN分类器学习指导更新目标/背景模型，以置信度为衡量标准减少迭代模型中产生的分割错误，避免错误被放大。通过实例自然图像对不同算法进行比较，实验结果表明本文算法在准确性和鲁棒性等方面具有更好的性能。除了在自然图像分割上的应用，本文中的算法为进行交互式医学图像分割提供了新的思路。随着医学影像技术的发展，医学图像分辨率越来越高，细节越来越多，自动图像分割技术难以获得令人满意的结果。本文算法可以通过用户输入信息准确地从复杂背景中分割出感兴趣目标，如肿块分割、肿瘤靶区勾画，提升图像分割的性能。

本文仍有一些问题有待进一步研究：提升分割算法对初始种子点选取的鲁棒性；KNN分类学习训练时，除了颜色空间和位置空间的特征向量，是否有其他的特征向量能进一步提高分类器评估标签的置信水平；除了使用KNN学习外，其他半监督学习是否也能提升graph cuts分割的准确性和鲁棒性。