汽车四轮转向最优控制技术的研究

姚世鹏,熊 欢，兰晓霞，罗 辑，曾 龙，陈习洲，荣 军,2



汽车四轮转向最优控制技术的研究

姚世鹏1,熊 欢1，兰晓霞1，罗 辑1，曾 龙1，陈习洲1，荣 军1,2

（1. 湖南理工学院信息科学与工程学院，湖南岳阳 414006；2. 复杂工业物流系统智能控制与优化湖南省重点实验室， 湖南岳阳 414006）

研究了汽车四轮转向最优控制技术。首先给出了汽车四轮转向数学模型，然后详细介绍了汽车四轮转向最优控制的工作原理，特别是对其最优控制系统的能控性和能观性进行证明，最后通过仿真软件对理论分析进行了仿真验证，通过对仿真结果的分析得出：在低速和高速运行时，汽车四轮转向最优控制具有良好的动静态特性。相对于基于横摆角速度反馈控制系统，最优控制系统的稳定性更好。

汽车四轮转向 最优控制 仿真

0 引言

四轮转向（4WS）控制技术就是在汽车行驶转向时通过引入一定的后轮转向来增强汽车在高速行驶或者在侧向风力作用下的操纵稳定性、行驶安全性及改善低速时汽车的机动灵活性。相对于二轮转向（2WS）控制技术低速度驾驶时转向响应迟缓，回转半径较大以及不能做到灵活转向的缺点，四轮转向控制技术在低速度转向时，前后轮作异相位的转向，可减小汽车转弯时的最小半径，获得较高的机动性；同时其在高速度转向时，前后轮作同相位的转向，可减小汽车的质心侧偏角，降低汽车的横摆角速度与侧向加速度两者之间的相差，可使轮胎侧向力裕度增大，使它避免达到饱和状态，提高汽车的防侧滑能力，让汽车在高速度行驶下的操纵稳定性得到显著提高[1,2]。

1 汽车四轮转向动力学数学模型的建立

在汽车四轮转下控制系统分析中，通常将汽车简化为一个二自由度的两轮车模型，如图1所示，其简化模型的运动微分方程为[2]：

考虑到前、后轮转角较小，近似认为cos=1，cos=1，则式（1）可写为：

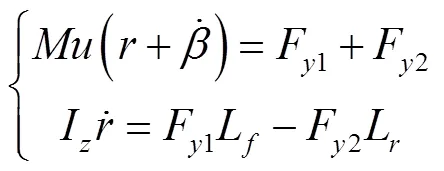
其中式（1）和（2）中相关参数的含义可参考文献[2]。

图1 二自由度四轮转向汽车模型

2 四轮转向汽车最优控制的工作原理

为了研究方便采用二自由度汽车4WS模型,将汽车简化成投影于地面上的高度不计的两轮车，假设轮胎侧偏角特性处于线性范围，汽车的行驶速度一定，忽略它的侧倾和俯仰运动，只考虑它的侧向和横摆运动。所建立模型的运动微分方程为式（3）所示[3,4]。

通过观察运动微分方程可知：前轮转角和后轮转角之和主要影响汽车的侧偏运动；前、后轮的差主要影响汽车的横向摆动。考虑到驾驶员的转向操作控制前轮转角，控制器根据汽车的横摆角速度和质心侧偏角信息反馈控制前轮和后轮转角。前轮转角和后轮转角可以通过以下方程式给出：

其中式（5）中：

输出方程为：

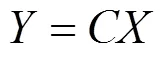
为了实现4WS的最优控制，首先得分析四轮转向系统的可控性与能观性。根据系统的状态变量来提供最优反馈增益即从而实现最优控制。如果对四轮转向系统的状态可控，那么就可以得到最优控制状态，实现质心侧偏角最小化的目的；否则的话，就谈不上最优控制。如果四轮转向系统具备可观测性，那么就可以通过观测输出量在一定时间内的变化，然后辨识出系统状态，从而可对4WS系统实行最优估计及最优控制。接下来对4WS系统的能控性和能观性进行研究[5,6]。

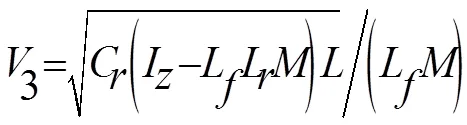
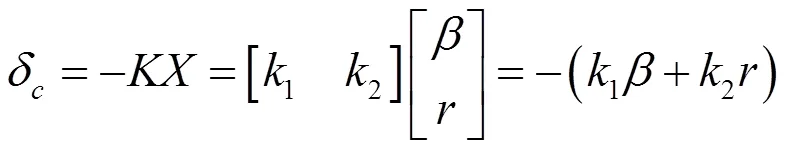
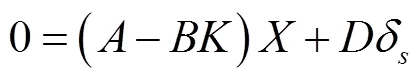
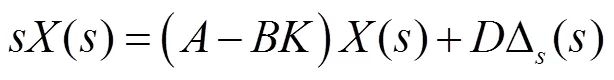
整理得到：

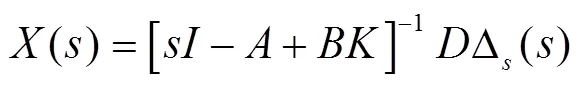
将输出方程（6）与式（14）联立可得：

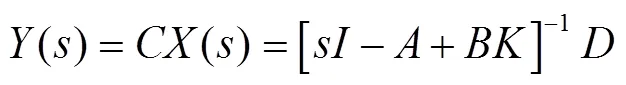
于是得到4WS系统的传递函数矩阵为：

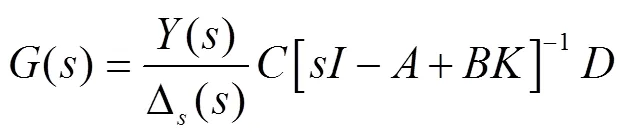
该传递函数矩阵为2×1阶列阵，第一行为4WS系统质心侧偏角对前轮转角的传递函数，第二行为4WS系统横摆角速度对前轮转角的传递函数。

3 最优控制仿真结果及分析

在低速（30 km/h）四轮转向汽车最优控制系统的矩阵计算结果为：

由图2可以得出：在低速情况下，采用最优控制的4WS车辆与2WS汽车相比，其质心侧偏角的瞬态响应性能得到明显改善，能很快地达到稳态值，超调量明显减小，汽车的运动姿态可得到了很好的控制。

（注：实线为4WS系统；点画线为2WS系统）

由图3得出：采用最优控制的4WS汽车的横摆角速度响应曲线与2WS车辆的基本一致，超调量有所减小，调节时间减小，这样能使驾驶员很好地保持原有的转向感觉。

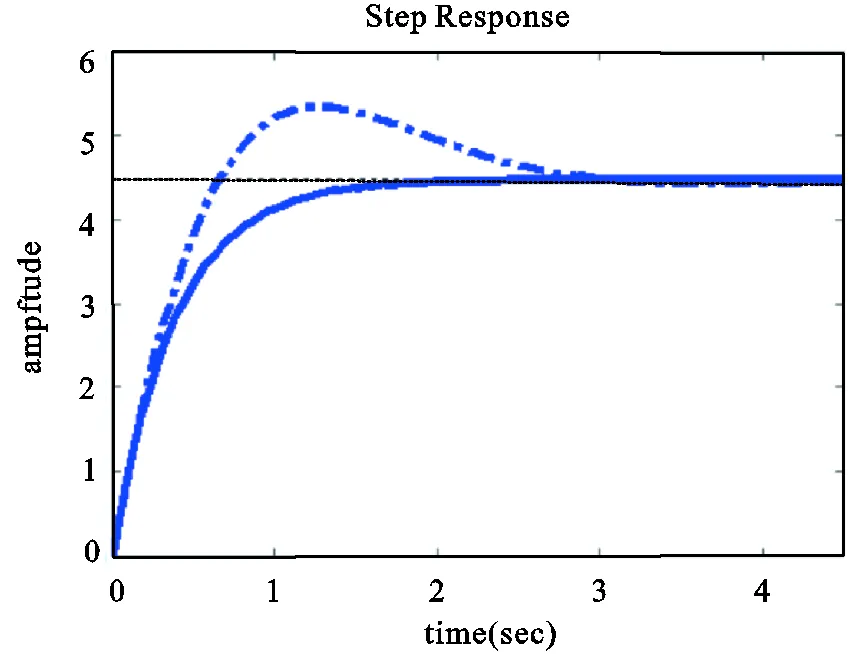
图3 低速时横摆角速度响应曲线

（注：实线为4WS系统；点画线为2WS系统）

在高速（90 km/h）四轮转向汽车最优控制系统的矩阵计算结果为：

四轮转向汽车最优控制系统的质心侧偏角和横摆角速度响应曲线如图4和图5所示。由图4和图5可以看出，高速时，2WS汽车的质心侧偏角比较大，而采用最优控制的4WS车辆可以有效地保证质心侧偏角接近为0。与2WS汽车相比，4WS车辆的横摆角速度响应迅速，很好地实现了驾驶员的转向意图，同时准确地跟踪了期望的横摆角速度。

为了更好得出四轮转向汽车最优控制的优越性，本文给出了四轮汽车最优控制和基于横摆角速度反馈控制的对比仿真波形如图6和图7所示。从图7和图8中可以看出：基于最优控制的四轮转向系统与基于横摆角速度反馈控制的四轮转向系统比较，前者的横摆角速度响应曲线达到稳定值的时间更短，且不存在超调量；它的质心侧偏角响应曲线明显优于后者，能够有效地保证质心侧偏角接近为0，使得工作性能指标达到极值，让汽车具有更好的操纵稳定性和行驶状态。

图4 高速时质心侧偏角响应曲线

（注：实线为4WS系统；点画线为2WS系统）

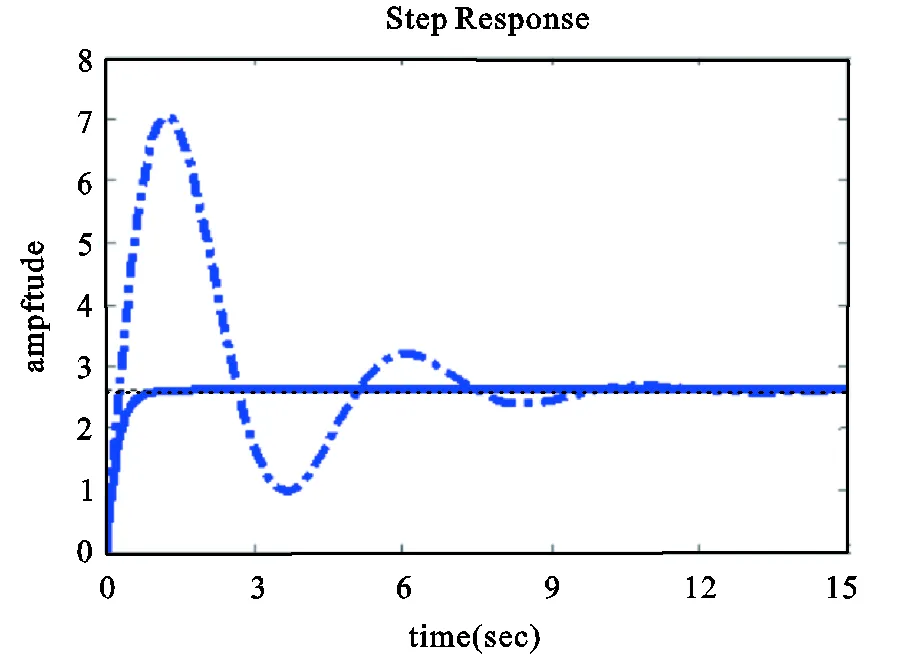
图5 高速时横摆角速度响应曲线

（注：实线为4WS系统；点画线为2WS系统）

图6 两种控制系统的仿真分析曲线

（注：低速（30 km/h）转向时,曲线1,2分别为横摆角速度反馈控制四轮转向系统和最优控制四轮转向系统的横摆角速度响应曲线。）

图7 两种控制系统的仿真分析

（注：高速（90 km/h）转向时，曲线3,4分别为最优控制四轮转向系统、横摆角速度反馈控制四轮转向系统的质心侧偏角响应曲线。）

4 结论

综上所述，本文研究了四轮转向汽车最优控制技术，通过对最优控制技术的研究发现其在低速和高速情况下，最优控制系统具有良好的动静态特性，特别相对于基于横摆角速度反馈控制系统，最优控制的汽车横摆角速度响应曲线达到稳定值的时间更短，且无超调，而且其质心侧偏角响应曲线明显优于基于横摆角速度反馈控制系统。

[1] 王智晶. 汽车四轮转向控制方法研究及模型车试验系统设计[D]. 重庆：重庆交通大学, 2010.

[2] 彭锦. 基于横摆角速度反馈的汽车四轮转向控制研究[J]. 湖南理工学院学报(自然科学版), 2017, 30(3): 38-43.

[3] 祁永宁, 陈南, 李普. 四轮转向车辆的直接横摆力矩控制[J]. 东南大学学报(自然科学版), 2004, 34(4): 451-454.

[4] 陈庆障, 孟杰, 刘臣富. 汽车四轮转向的最优控制研究[J]. 常熟理工学院报, 2016, 30(2): 4-8.

[5] 田承伟, 宗长富, 何磊,等. 汽车线控四轮转向控制策略[J]. 吉林大学学报(工学版), 2010, 40(5): 1177-1182．

[6] 刘泽明, 黄妙华, 周亚鹏. 四轮转向车辆操纵稳定性仿真分析[J]. 时代农机, 2015, (2): 63-64.

[7] 雷敏. 基于MATLAB的四轮转向电动汽车横向稳定性控制仿真研究[J]. 时代汽车, 2017, (3): 73-74.

[8] 于蕾艳, 林逸, 施国标. 四轮线控转向系统的转向控制策略研究[J]. 计算机仿真, 2008, 25(4): 278-281.

Research on the Optimal Control Technology for Automobile Four Wheel Steering

Yao Shipeng1, Xiong Huan1, Lan Xiaoxia1, Luo Ji1, Zeng Long1, Chen Xizhou1, Rong Jun1,2

(1. Department of Information Science and Engineering, Hunan Institute of Science and Technology, Yueyang 414006, Hunan, China; 2. Key Laboratory of Hunan Province on Intelligent Control and Optimization of Complex Industrial Logistics System, Yueyang 414006, Hunan, China)

U461

A

1003-4862（2018）11-0033-04

2018-06-11

湖南省科技计划项目经费资助（2016TP1021）

姚世鹏（1998-），男。研究方向：自动化。Email: 2438514819@qq.com

荣军（1978-），男，副教授。研究方向：开关电源和电机控制。E-mail: rj1219@163.com