UPVC斜三通阻力损失及流动特征数值模拟
石 喜,陶 虎,柴媛媛,万冰清
(1.兰州交通大学土木工程学院,兰州 730070;2.甘肃省水土保持科学研究所,兰州 730020)
三通管在水利、市政、化工等流体输送管网中大量使用,其作用是增加出水口,改变流体的流动方向。受体型变化的影响,通过三通管的水流流态较为复杂,往往伴随着旋涡及二次流的产生,致使其阻力规律复杂。然而在管网水力计算时,三通管的局部阻力损失计算一般按照沿程阻力损失的一定比例或按水力手册中固定系数值乘以流速水头计算,实际上其阻力系数不是一个定值,而是与雷诺数、分流比、形状变化参量等因素有关,即ζ=f(Re,q,φ),尤其在一些短管的水力计算中,局部阻力损失可能占的比重较大,如果按照固定值或沿程阻力损失的一定比例计算可能导致水力计算不准确。
国内外不少学者对分岔管流进行了研究,Blaisdell和Manson[1]对不同角度分岔管的水头损失进行了研究,认为水头损失系数与流量比呈二次抛物线关系。Gan和Saffa[2]利用CFD技术对空气在T型管内的流动进行了数值模拟。Costa等[3]对直角和圆角的90°三通管进行研究,表明圆角三通管能使水头损失减少10%~20%。高学平[4]、杨校礼等[5]利用紊流模型对某抽水蓄能电站月牙肋岔管的水力特性进行了数值模拟,分析了水头损失及流态变化。李玲等[6]对分岔角为64°的三岔管内水流的流动进行了数值模拟与实验研究,表明无论水头损失还是三岔管内水流的流动模式,计算与实验吻合得较好。郑文玲等[7]对重力输水管网岔管在6种不同工况下的流速、压强分布及水头损失进行了研究,认为岔管处的水力特性复杂、影响因素较多,具体问题应具体分析。汪建兴等[8]对细小直角弯管流道进行了数值模拟,认为CFD技术可以很好的模拟转弯处的二次流。上述主要研究抽水蓄能电站中分岔管在发电工况和抽水工况下的阻力及流场特性,而针对不同管道流量变化对岔管水流阻力及流场影响的研究较少。本文采用数值模拟的方法对灌溉输配水管网中UPVC斜三通管的阻力损失和流场特征进行研究,以期为管网的水力计算提供一定参考。
1 计算模型与方法
1.1 湍流模型
描述不可压缩水流运动的基本方程可由连续性方程、N-S方程等构成,具体表达形式见文献[9]。由于三通管的流动属于湍流,本文选用标准的k-ε湍流模型进行计算,其湍动能与耗散率的输运方程为:
Gk+Gb-ρε-YM+Sk
(1)
(2)
式中:μt为湍流黏性系数;Gk,Gb分别为平均速度梯度和浮力作用引起的紊流湍动能;YM为脉动扩张引起的动能耗散率;C1ε、C2ε、C3ε、σk、σε为为常数;Sk、Sε为用户定义的源项。
1.2 计算模型与网格划分
斜三通管的几何模型见图1(a),三通管分别由主管、斜管和直管组成,斜管的分岔角度为45°。所有管段均为DN75管道,管壁厚度3 mm,其内径为69 mm,UPVC管的相对粗糙度为0.03 mm。为了充分保证三通管内的流态稳定,取压点分别设置在上游5倍和下游8倍的管径处。计算水流的温度为20 ℃,运动黏度ν=1.007×10-6m2/s,取主管流速为2.5 m/s,则主管雷诺数Re=171 301。
几何模型建好后对模型的计算区域进行网格划分,为了保证计算精度,在三通管分岔处采用非结构四面体网格进行局部加密,其余部位采用结构化六面体网格,共划分网格数96.8万个,网格划分示意图见图1(b)。

图1 斜三通管几何模型与网格划分Fig.1 Geometric model and mesh division of slope tee pipe
1.3 离散方法与边界条件
控制方程的离散采用有限体积法,压力与速度的耦合采用SIMPLE算法迭代计算,扩散项采用中心差分格式离散,对流项采用二阶迎风格式离散,对近壁面的处理近似采用标准壁面函数法。边界条件主管设置为速度进口,速度为2.5 m/s,斜管和直管均采用自由出流边界,分别设置不同的分流比进行计算。各项的收敛残差为0.000 1。
1.4 数值模型验证
为了验证标准k-ε湍流模型在三通管水流计算中的准确性,本文建立了文献[7]中卜型岔管在正常蓄水位时供水工况下的数值模型,将计算结果与其试验结果进行对比,其中岔管岔角55°,划分网格数为133.9万个,计算结果如表1所示。从表中可以看出,在不同供水工况下,阻力系数的数值模拟计算结果与试验结果偏差较小,最大相对偏差为14.3%。表明标准k-ε湍流模型在计算分岔流动中具有较高的精度,因此可用于三通管流动的模拟计算。
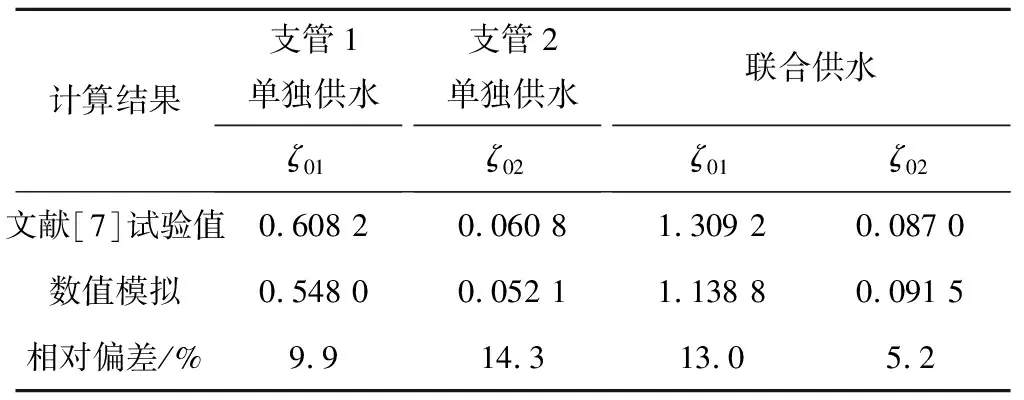
表1 数值模拟结果与文献[7]中试验结果对比Tab.1 Comparison of numerical simulation results with experimental results in document[7]
注:ζ01、ζ02分别为主管至岔管、主管至直管的阻力系数。
2 结果与分析
2.1 局部阻力系数的变化
对于如图1(a)所示的斜三通管,根据伯努利方程[10],主管至斜管、主管至直管断面间的能量守恒关系式为:
(3)
(4)
式中:p为对应的压强;α为动能修正系数;λ为沿程阻力系数;v为断面平均流速;ρ为流体密度;d为管径;ΔP01、ΔP02分别为主管至斜管、主管至直管之间的局部水头损失。
由于UPVC管道内壁面极其光滑,其水流流态一般处于水力光滑区,不同管段沿程阻力系数的计算可通过文献[11]中通过UPVC管试验得到的公式:
(5)
式中:Re为不同管段对应的雷诺数。
三通管的局部阻力系数计算公式为:
(6)
(7)
式中:ζ01、ζ02分别为主管至斜管、主管至直管的局部阻力系数。
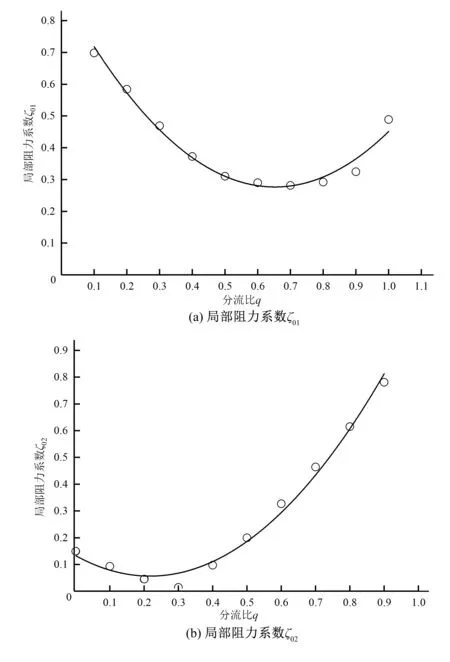
图2 局部阻力系数随分流比q的变化Fig.2 Local resistance coefficient variation with flow ratio q
定义三通管的分流比q=Q1/Q0,其中Q0、Q1分别为主管和斜管的流量。在探讨三通管局部阻力系数时,应考虑雷诺数Re、形状参量φ及分流比q等参数的影响,根据相关研究表明[12],对于形变件而言,水流流态在小于相同管径直管段的转捩雷诺数时提前进入阻力平方区,文献[13]对正三通管的试验结果表明,在Re>1.5×105之后雷诺数对阻力系数的影响甚微,本次计算雷诺数Re=171 301,可认为水流已进入阻力平方区,不考虑雷诺数的影响。由于计算的斜三通管为特定形状,也不考虑形状参量的影响,仅探讨阻力系数随分流比的变化。图2分别给出了为主管至斜管、主管至直管的局部阻力系数ζ01、ζ02随分流比q的变化关系。从图2中可以看出,ζ01、ζ02均随q的增大呈先减小后增大的趋势,与分流比q呈较好的抛物线关系,ζ01在q=0.7左右达到最小值,ζ02在q=0.3左右达到最小。通过拟合得到ζ01和ζ02随q变化的关系表达式,相关系数R2分别为0.977 8、0.988 9。
ζ01=1.445 7q2-1.886 2q+0.892 1
(8)
ζ02=1.619 9q2+0.702 3q+0.133 1
(9)
2.2 压力分布
图3为不同分流比时三通管中心剖面的压力云图,由图3可以看出,由于分岔处水流分流,导致分岔处水流压力分布不均匀,随着分流比q的不同而不同。在q=0时,通过斜管的流量Q1=0,斜管的压力最大,受斜管水流运动的影响,使直管内壁处出现局部低压区;在q=0.2和q=0.5时,由于斜管有流量通过,在分岔处水流摩擦碰撞在直管内壁处出现局部高压区;在q=0.8,直管的流量较小,斜管内壁出现局部低压区;q=1.0时,水流全部由斜管流过,直管的压力最大,使得斜管内压力变化复杂。由压力变化可以看出,主管至斜管、主管至直管的压差变化呈先减小后增大的趋势。
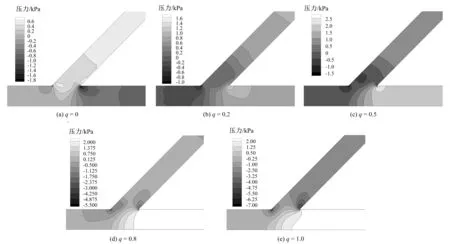
图3 斜三通管中心剖面压力云图Fig.3 Pressure cloud map in center section of slope tee pipe
2.3 流速分布
图4为不同分流比时三通管中心剖面的速度云图,可以看出不同分流比时分岔处的速度分布均匀程度及扰动范围不一致。在分流比q=0时,由于斜管的流速v=0,水流经过分岔处对斜管水流撞击使得主管和直管进口的流速分布不均匀,内壁流速较低,外壁流速较高;在q=0.2和q=0.5时,主管和直管的流速分布较为均匀,斜管的流速梯度较大,表现为内壁速度较大,外壁速度较小;在q=0.8和q=1.0时,随着进入斜管流量的增多及分岔水流发生转向导致主管和斜管的流速分布都不均匀,流速梯度较大,在斜管内、外壁出现低速区,中间出现高速区。分析可知,流速分布的变化主要是由于分岔处水流方向发生转向和不同管段流量大小变化引起的。
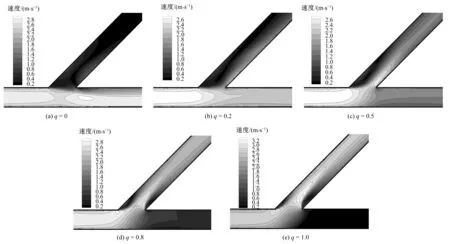
图4 斜三通管中心剖面速度云图Fig.4 Velocity cloud map in center section of slope tee pipe
2.4 流线分布图
图5给出了不同分流比时三通管中心剖面的流线图,由图5可以分析:①主管进入斜管的水流流动特征:当分流比q=0时,由于斜管不过流,从主管流过的水流在分岔处对斜管的水流进行撞击,在斜管进口位置由于剪切作用诱发产生较大的旋涡。当q>0时,在斜管进口外壁处由于水流环向作用产生的离心力诱发旋涡,旋涡尺度大小随分流比的增大而减小,在q=1.0时不产生旋涡,这是由于随着分流比的增大,进入斜管的流量增多,诱发产生旋涡的能力减弱;然而在分流比较大时,水流偏转角度增大,使得斜管的阻力损失增大,因此可分析主管至斜管的阻力损失主要是由离心力作用产生的旋涡和流量变化引起的,在分流比较小时,旋涡起主导作用,在分流比较大时,流量变化起主导作用。②主管进入直管的水流流动特征:当q=0时,由于受斜管旋涡的影响,导致进入直管的水流较复杂,此时主管至直管的阻力损失主要由斜管的旋涡引起;当q>0时,随着进入斜管水流的增多,水流偏转角度增大,受斜管的影响进入直管的水流也发生偏转,并且偏转角度也随分流比的增大而增大;当q=1.0时,进入斜管的水流对直管进口位置由于剪切作用诱发较大的旋涡产生,此时水流偏转角度最大。因此可分析主管进入直管阻力损失主要由水流发生偏转引起的。
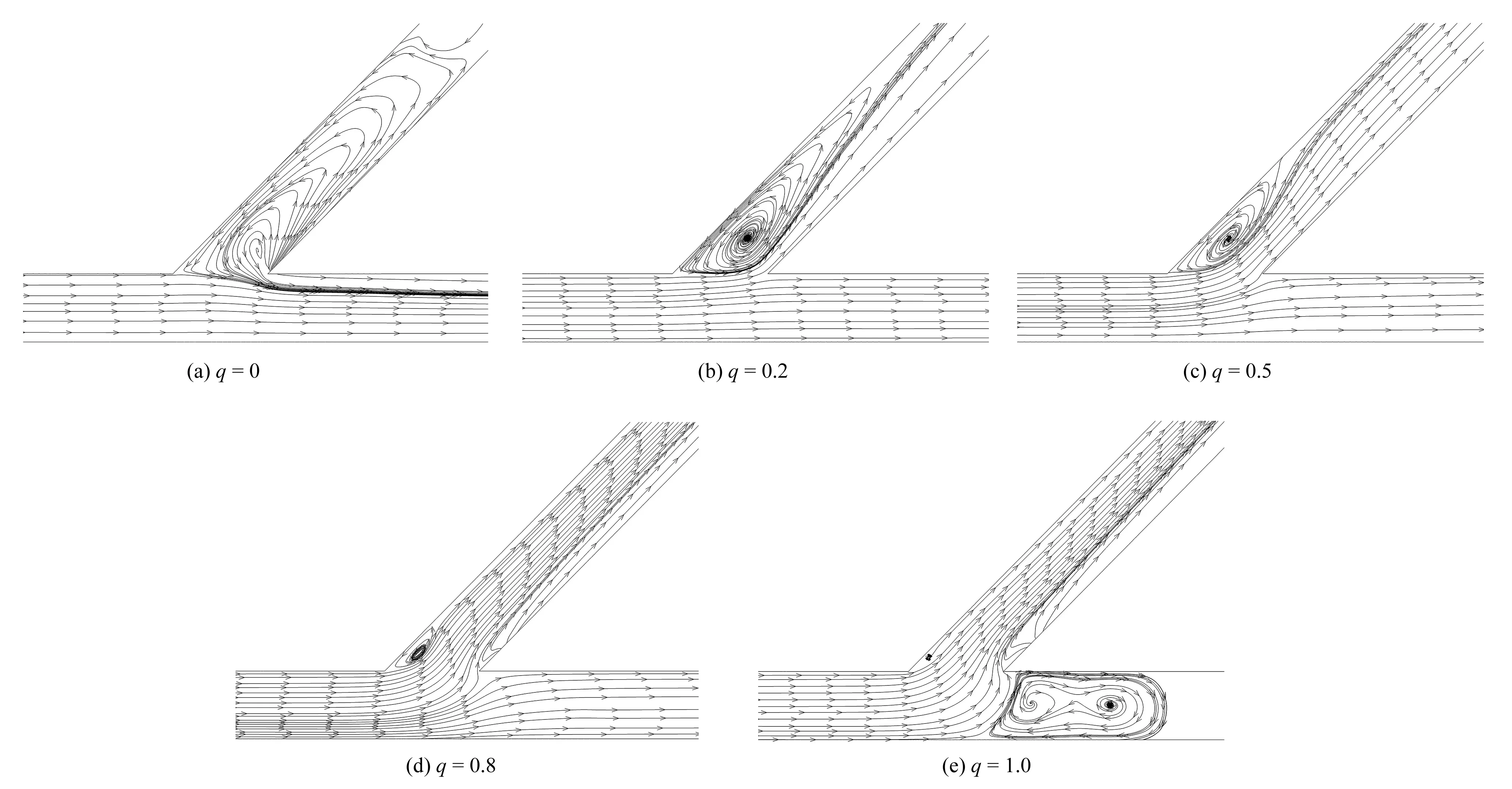
图5 斜三通管中心剖面流线图Fig.5 Streamline graph in center section of slope tee pipe
3 结 语
本文通过数值模拟的方法对UPVC斜三通管的阻力特性及流动特征进行了研究,得出以下结论。
(1)斜三通管主管至斜管、主管至直管的局部阻力系数均随分流比的增大呈先减小后增大的趋势,与分流比呈较好的二次抛物线关系。
(2)不同分流比时压力分布和流速分布变化不同,由分岔处水流方向发生转向和不同支管流量大小变化引起的。
(3)通过分析产生阻力损失的诱因:主管至斜管阻力损失主要是由离心力作用产生的旋涡和流量变化引起的,在分流比较小时旋涡起主导作用,在分流比较大时流量变化起主导作用;主管至直管阻力损失主要是由水流发生偏转引起的。
□

