基于Voronoi图的土工膜颗粒垫层随机重构模型

姜晓桢,田晓丹

(1. 南京水利科学研究院岩土工程研究所,江苏 南京 210024;2.河海大学文天学院,安徽 马鞍山 243031;3.河海大学水利水电学院,江苏 南京 210098)

在土石坝坝面土工膜防渗结构中,土工膜的垫层材料一般采用具有良好透水性的颗粒材料(碎石为主),以便及时排除膜下渗水[1]。但土工膜在水压力作用下,容易被垫层中颗粒顶破或在颗粒间隙内发生胀破。围绕土工膜在工程中所存在胀破和顶破的破坏形式,目前使用的SL/T 235—1999《土工合成材料测试规程》提出了3种标准试验来定性地衡量土工膜抵抗胀破和顶破的能力。由于是标准试验,所以试验中采用的试样、夹具以及顶杆的尺寸是一定的,无法真实还原颗粒垫层上土工膜的真实受力条件。在顶破胀破试验中,国外有学者采用呈等边三角形排布的3个刚性锥形凸起来模拟凹凸不平的垫层表面,但是由于锥形凸起的间距和尺寸是固定的,所以试验得出的结论无法推广到实际应用中[2-3]。事实上,颗粒垫层上土工膜顶破胀破现象除了与水压力大小和土工膜自身物理力学特性有关外,垫层颗粒形状、粒径级配、孔隙率等是更为重要的影响因素,所以也有不少学者采用真实的颗粒材料进行试验[4],但由于真实颗粒垫层中每一个颗粒的形状、粒径及位置是随机的,同时其与颗粒垫层的孔隙率、粒径级配等试验条件密切相关,所以采用真实颗粒进行试验时,常常无法对试验条件进行有效控制,同时受试验组数和试样大小的影响,想要获得具有统计意义的试验数据,试验的工作量较大。而数值模拟方法可以避免上述问题,特别是随着近些年来离散元数值模拟方法的不断进步,从单一的圆颗粒模型逐步发展出了可以考虑不同颗粒形状的数值模型[5-9],给颗粒垫层的随机重构以及颗粒形状参数的统计分析带来了便利。本文提出了一种基于Voronoi图的颗粒垫层随机重构模型,并与真实颗粒垫层进行比较分析,可为后续进一步研究土工膜在颗粒垫层上的顶破胀破概率与垫层颗粒形状、粒径级配和孔隙率之间的关系打下基础。

1 随机重构模型的基本要求

a. 颗粒垫层随机重构模型中颗粒形状、粒径级配与孔隙率尽可能与真实颗粒相近。由于土工膜在颗粒垫层上一般是被不规则形状的颗粒顶破,所以采用不规则的多边形颗粒进行模拟比较合理。在级配良好、孔隙率较小的颗粒垫层中,小颗粒能够有效地填充大颗粒之间的间隙,同时小颗粒之间的间隙尺寸也要比大颗粒之间的间隙尺寸小,增加了土工膜与垫层颗粒的接触面积,这将降低土工膜在垫层颗粒上发生顶破胀破的可能性,所以粒径级配与孔隙率也与土工膜的顶破胀破有关。

b. 由于真实的垫层颗粒之间不存在重叠,同时也不存在受力不平衡的悬浮颗粒,所以要求颗粒垫层的随机重构模型中,相邻颗粒之间的重叠量要尽可能小,且每个颗粒均能通过相邻颗粒之间的接触关系实现受力平衡,需要尽可能提高算法精度从而减小颗粒间的重叠量,同时避免受力不平衡的悬浮颗粒的出现。

c. 模型中需要设置一定的随机过程,随机过程及其参数会对模型中的颗粒形状、粒径级配和孔隙率等产生影响,通过调整这些随机过程的设置方法及其参数,能够达到控制颗粒形状、粒径级配和孔隙率等性状的目的。

目前常用的离散元颗粒模型建模方法大致可分为3种:①下落法[10-12]。下落法按颗粒级配以及形状的要求建立有限数量的一组颗粒,并通过离散元模型施加重力,模拟颗粒自由下落堆积的过程。该方法最主要的问题在于无法控制自由下落堆积而成的颗粒堆积体的孔隙率,且建模的效率较低。②膨胀法[13-15]。膨胀法先在指定区域内生成小颗粒,然后增大颗粒半径使得颗粒发生接触,并通过接触力使得颗粒发生运动,充满整个模型空间。该方法虽然能够较好地实现孔隙率及粒径级配的模拟,但其粒径的增大系数难以控制,常常造成颗粒间有很大的重叠接触,颗粒间以及颗粒与模型边界之间存在较大的接触力,颗粒间的接触力瞬间释放会造成大量颗粒飞溢出边界,导致结果不准确。③纯几何法[16-17]。纯几何方法中,颗粒体的堆积纯粹基于几何计算,不模拟颗粒的动力特性,所以建模效率较高,但其同样无法控制孔隙率。

2 基于Voronoi图的随机重构模型

Voronoi图,又称泰森多边形或Dirichlet图,它是一组连接两邻点直线的垂直平分线所组成的连续多边形,是一种重要的图形几何结构[18]。Voronoi图在随机模型中有着广泛的应用,其基本概念可形象地描述为:在区域内有n个火源(形核点),这n个火源同时点燃,并以相同速度向所有方向蔓延,当两个火源扩散后相遇时熄灭,那么燃烧熄灭处所形成的图便是Voronoi图[19]。

2.1 形核点的位置

要生成Voronoi图,首先要确定形核点的位置。显而易见,当形核点在区域内规则排布时,生成的Voronoi图及其多边形也是规则的,如图1(a)所示,所以形核点的位置应具有一定的随机性,使得生成的Voronoi图中的多边形形状及大小产生随机性。文中形核点位置产生的随机过程如下:

图1 多边形颗粒形核点位置示意图

a. 在某二维区域([xmin,xmax], [ymin,ymax])内,以颗粒最大粒径dmax为边长生成正方形网格,正方形网格形心位置为形核点的初始位置。

b. 对于每个形核点位置进行随机偏移,即形核点坐标增加一个随机偏移量:

xi=xini+N(-ks,ks)

yi=yini+N(-ks,ks)

(1)

式中:xini与yini为初始位置坐标;N为随机数;ks为N的取值范围。本文采用[-ks,ks]的均匀分布,ks的取值不能大于dmax,即形核点位置偏移后仍在正方形网格内,一般取dmax的1/4～2/3较为适宜。同时ks的大小会对多边形的形状和大小产生影响,如图1所示,随着ks取值的增大时,Voronoi图的各个多边形之间的差异也随之增大,即随机性也增大。

2.2 孔隙率的控制

确定形核点位置后产生的Voronoi图中多边形颗粒是闭合的,相互之间不存在孔隙,此时为颗粒垫层最紧密的状态,可通过一定的手段对每个多边形进行变换使得多边形颗粒之间产生孔隙。

通过观察可知,由于Voronoi图中相邻的多边形之间共有一条边,所以多边形之间没有孔隙,可以通过在共有边上随机生成新的点作为两侧的多边形顶点,从而“制造”出孔隙。如图2所示,在一条共有边上随机生成4个点,在随机生成条件下,点与点之间的距离有可能非常小,有的可能接近重合,此时,可产生不同的颗粒间接触的情况:①颗粒P与颗粒M之间的情况(边M1M2全部包含在边P1P2内);②颗粒L与颗粒M之间的情况(边L11L12与边M11M12部分包含);③颗粒P与颗粒L之间(颗粒P以顶点P11与颗粒L的边L1L2相接触);④颗粒L与颗粒N之间接触边顶点L8与顶点N2相互重合;⑤颗粒M与颗粒N之间顶点N5与M9重合,顶点N4与M10也重合;⑥两个颗粒以点对点的方式接触,由于随机条件下出现这种情况的概率非常小,所以未在图2中绘出。

图2 多边形颗粒顶点位置变换产生孔隙示意图

由图2可知,在共有边上生成的新顶点位置决定了孔隙的大小,当新顶点均与原顶点重合时,模型的孔隙率最小为零,当颗粒与颗粒之间均是点对点接触时,模型能达到最大的孔隙率,所以可通过控制新顶点产生的随机过程,实现对颗粒垫层随机重构模型孔隙率的控制。本文采取以下方法进行孔隙率的控制:

a. 确定共有边上产生新顶点中相距最远的两点间线段Lr，其长度为

lr=kr(μr,σr,0,1)lp

(2)

式中:lp为共有边的长度;kr为取值范围在0～1的随机数,本文采用正态分布产生kr;μr为kr的均值;σr为kr的标准差。

b. 通过确定线段Lr的起点来确定线段Lr的位置:

xp=x1+(lp-lr)kp(μp,σp,0,1)cosθ

yp=y1+(lp-lr)kp(μp,σp,0,1)sinθ

(3)

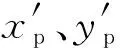
c. 在线段Lr内再随机产生2个点,将产生的新顶点(包含最大线段Lr的两个端点)随机划分给共有边两侧的多边形,从而形成新的多边形,若新多边形之间相互不接触,则重新进行随机划分,直至满足相互接触的条件。

根据上文可知,控制孔隙率的参数有2个,分别为kr和kp。随机数的均值和标准差会对孔隙率产生影响,表1和表2分别给出了kr和kp在不同均值和标准差条件下的颗粒垫层的孔隙率。

表1 参数kr不同均值和标准差时的模型孔隙率

注:“/”表明在该组均值和标准差条件下,kr不在[0,1]内的概率较高,故舍去。

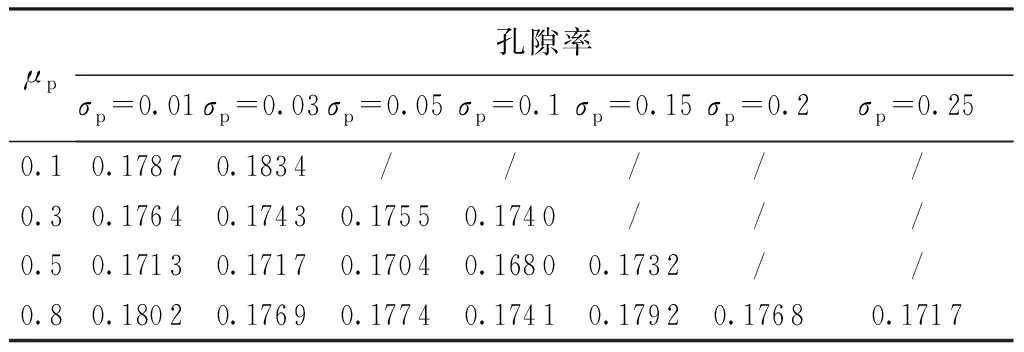
表2 参数kp不同均值和标准差时的模型孔隙率

注:“/” 表明在该组均值和标准差条件下,kp不在[0,1]内的概率较高,故舍去。

由于颗粒垫层的孔隙率主要由线段Lr的长度lr决定,所以从表1中可以看出,随着kr的均值μr的增大,孔隙率不断减小,而由于标准差σr只对kr的离散程度有影响,所以其对孔隙率的影响很小。从表2可以看出μp和σp取值大小与孔隙率的关系不大,说明Lr的起点位置与孔隙率的关系也不大,且从表2可以看出,其孔隙率基本与表1中μr=0.5一行的孔隙率相接近,说明只要当随机过程的参数相同时,生成的随机重构模型孔隙率也相近,可见该模型的重复性较好。

2.3 粒径级配的控制

对于多边形颗粒来说,颗粒的几何尺寸参数较多,不同文献采用了不同的方法定义多边形颗粒的粒径[20-22]。本文采用多边形颗粒边界的最小Feret直径作为颗粒粒径,即颗粒边界上不同方向上外切平行线间距的最小值,其值代表了颗粒所能通过的最小筛孔的孔径。

从图1可以看出,多边形颗粒的形核点的位置不同,颗粒的粒径就会变化。图3为不同的ks时模型的粒径级配曲线,随着ks的增大,粒径级配曲线略有变化,但变化的幅度很有限,粒径分布范围较窄。可见通过改变ks,只能得到粒径大小较为均匀的模型,并不能对模型的粒径级配进行进一步的调整。本文通过设置颗粒的随机分裂过程,产生粒径较小的颗粒,以实现粒径级配调整的目的。具体步骤如下:

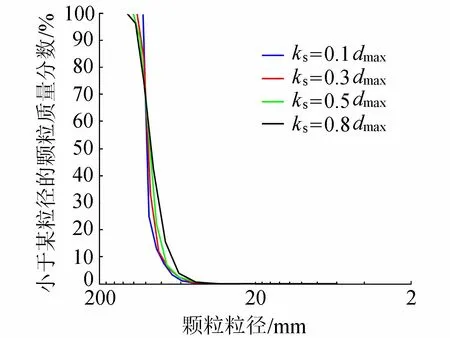
图3 不同ks值时粒径级配曲线

步骤1通过颗粒粒径来计算其分裂的概率Pf:

(4)

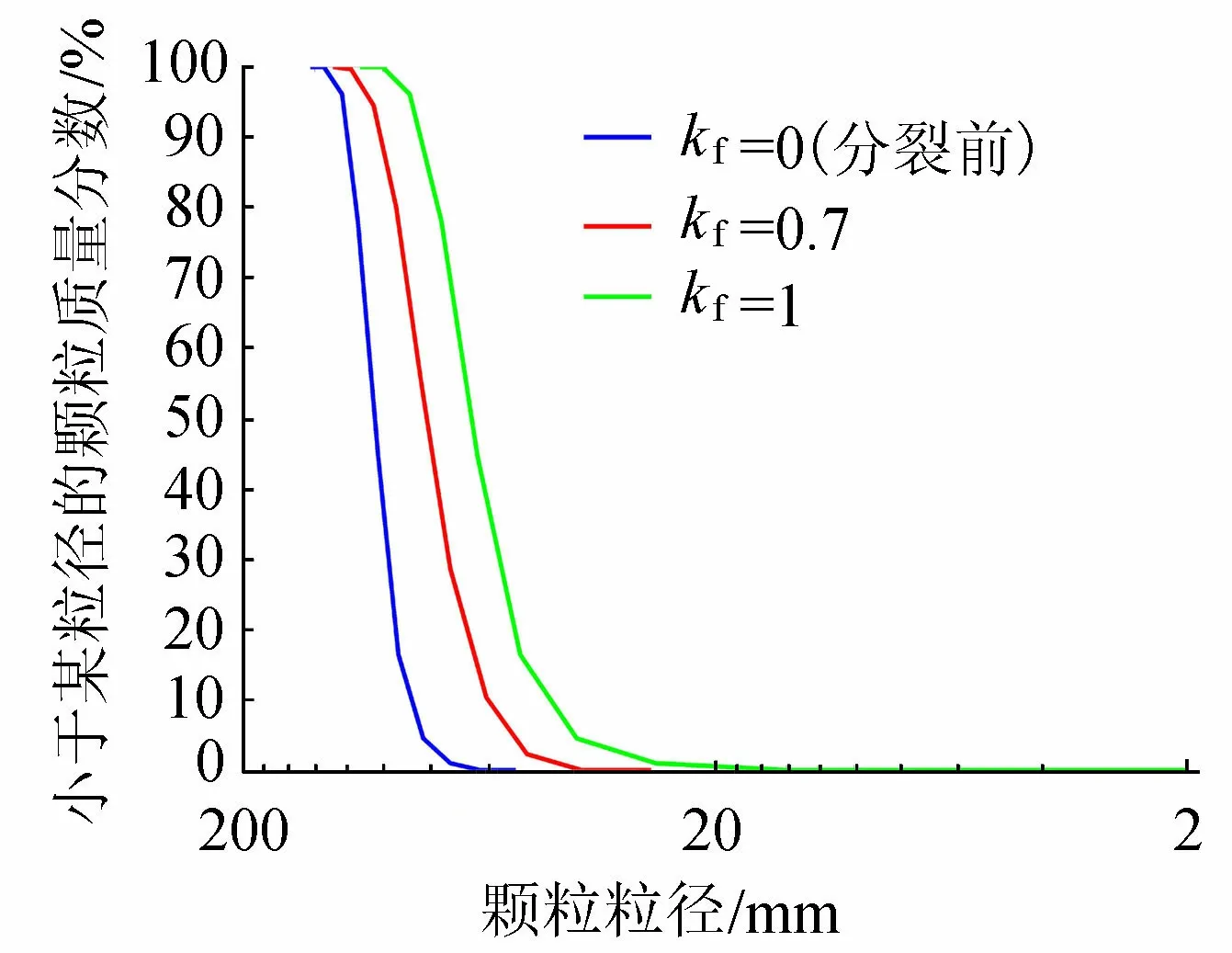
式中:dmax为颗粒的最大粒径;dmin为颗粒的最小粒径;di为该颗粒的粒径。在0～1的范围内通过均匀分布取一个随机数Pi,若Pi

步骤2在需分裂的多边形颗粒内以形心为原点建立一个坐标系,x轴与水平方向的夹角φ为0°～360°之间的一个随机数(通过均匀分布产生)。

步骤3该坐标系的x轴与y轴会与多边形颗粒的轮廓产生4个交点,通过连接多边形颗粒形心与这4个交点形成4条线段,并在每条线段上通过均匀分布随机取1个点,共产生4个随机点,将每个需分裂的多边形颗粒内产生的随机点和原有的形核点一起作为新的形核点绘制Voronoi图,从而实现颗粒的一次随机分裂。

由于颗粒分裂是随机地在原有的颗粒内部产生新的形核点,所以重新生成的模型中势必产生了更小粒径的颗粒,同时由于颗粒是按概率分裂,所以原有的大粒径颗粒也能有部分得以保留,从而使得模型的粒径级配曲线变得长而缓,不均匀系数明显增大。若一次分裂后的粒径级配曲线仍不满足要求,则可重复颗粒分裂过程,直至满足要求(见图4,图中Cu为不均匀系数,Cc为曲率系数)。当然也有可能存在所需的粒径级配曲线恰好落在某一次分裂前后颗粒粒径级配曲线之间的情况,此时,可按式(5)调整颗粒分裂的概率:

(5)

式中:kf为颗粒分裂控制系数,取值范围0～1,其值越小,代表大粒径颗粒分裂的概率越小,分裂后级配曲线中大粒径的颗粒占比越大,从而实现对模型级配进一步优化调整的目的。图5为不同kf时颗粒粒径级配曲线。

图4 颗粒随机分裂后粒径级配曲线

图5 不同kf值时颗粒粒径级配曲线

图6为在长10 m、高2 m的二维范围内采用本文方法生成的颗粒垫层随机重构模型,由于控制孔隙率的操作只是在共有边上产生新的顶点,对颗粒的最小Feret直径几乎没有影响,所以颗粒垫层随机重构模型可先进行粒径级配控制,得到满足要求的级配曲线后,再按给定的孔隙率进行孔隙率控制,最终得到级配和孔隙率都满足要求的颗粒垫层随机重构模型。

图6 颗粒垫层随机重构模型的建立过程

3 模型颗粒与真实颗粒的形状比较

3.1 颗粒形状参数选择

为了对比随机重构模型中颗粒与真实颗粒的形状,首先要确定评价颗粒形状的量化参数。关于颗粒形状表达与评价方法的研究比较多,在尺度上可概括为3个层次:①整体轮廓(球状、柱状、片状等);②棱角性(磨圆程度);③表面纹理[20-22]。对于颗粒垫层上土工膜的顶破胀破现象而言,其尺度一般只到第②层次,所以本文选择了扁平度e(第①层次)和磨圆度q(第②层次)这2个形状参数进行分析比较,计算公式如下:

(6)

(7)

式中:Fmax分别为最大、最小Feret直径;PE为等效椭圆(扁平度和面积与颗粒都相同的椭圆)的周长;Pc为颗粒轮廓的实际周长。

3.2 真实颗粒形状参数采集

目前数字图像分析方法作为颗粒形状测量的手段已经广泛应用于岩土力学、材料力学等领域[20-22],本文采用高清数码相机采集真实颗粒的数字图像,并利用MATLAB软件中的Image tool工具箱[23]对图像文件进行分析从而获得真实颗粒的形状参数。图像分析方法的基本原理是通过设置灰度的阈值,将颗粒与图像的背景分离,形成黑白二值图像,从而提取颗粒轮廓边界,并对边界进行分析,最终得到所需的形状参数,这就需要颗粒颜色与背景颜色产生较大的反差,才能保证颗粒轮廓边界的准确采集和形状参数的准确计算。图7为部分真实颗粒的形状参数采集过程,其中颗粒来源于浙江某抽水蓄能电站面板堆石坝料场,为灰岩爆破料,颗粒数量为122个。

图7 真实垫层颗粒图像转化为黑白二值图像

3.3 形状参数对比

图8 颗粒扁平度与磨圆度散点图

由于随机重构模型的颗粒较多,所以采用随机抽样的方法抽取122个模型颗粒与真实颗粒进行对比。图8为模型颗粒与真实垫层颗粒的扁平度和磨圆度散点图。由图8可知，扁平度主要分布在1～2之间,其中落在1.2～1.6之间居多,模型颗粒样本的扁平度均值为1.67,标准差为0.45,真实颗粒样本的扁平度均值为1.44,标准差为0.28。磨圆度主要分布在0.85～0.95之间,且主要集中在0.90附近,磨圆度的分布范围要比扁平度窄,模型颗粒的磨圆度均值为0.908 4,标准差为0.037,真实颗粒的磨圆度均值为0.885 1,标准差为0.049。

根据扁平度和磨圆度的定义可知,扁平度为最大Feret直径与最小Feret直径之比,所以其值必然大于1,磨圆度为等效椭圆周长与颗粒实际周长之比,其值必然小于1。由于显著性检验中参数检验方法的前提是样本来源于正态分布(分布范围为[+∞,-∞])的总体[24],虽然目前尚未能完全确定扁平度与磨圆度符合何种分布,但从分布范围来说颗粒扁平度和磨圆度均不是正态分布,所以对模型颗粒与真实颗粒的形状参数统计分布的显著性检验只能采用非参数检验方法。本文采用Ansari-Bradley方法[25]对模型颗粒与真实颗粒的扁平度和磨圆度进行显著性检验,显著性水平均为0.05。检验结果显示:扁平度的显著性检验指标p=0.081 6>0.05,接受假设,即模型颗粒样本与真实颗粒样本的扁平度来源于同一总体分布;磨圆度的显著性检验指标p=0.353 0>0.05,接受假设,即模型颗粒样本与真实颗粒样本的磨圆度也来源于同一总体分布。

4 结 论

a. 参数ks用于控制Voronoi图中形核点位置,可生成无孔隙的初始模型,且初始模型颗粒粒径级配与参数ks之间关系不大,初始模型的粒径较为均匀。

b. 通过在初始模型中多边形颗粒的共有边上设置新的顶点,可生成带有孔隙的模型,模型的孔隙由参数kr和kp控制的随机过程来产生,其中参数kr控制的随机过程决定了模型孔隙率的大小。

c. 由于初始模型是根据颗粒的最大粒径建立的,所以调整颗粒粒径级配的过程是按颗粒粒径大小来确定颗粒分裂的概率,颗粒分裂过程可不断重复,直至获得满足要求的粒径级配,其中参数kf用于对颗粒分裂概率进行控制,以实现级配曲线在一次分裂中的微调。

d. 由于孔隙率的控制过程对颗粒的粒径影响很小,所以一般先进行粒径级配控制,再进行孔隙率控制,最终实现模型颗粒的粒径级配以及孔隙率与真实颗粒的相近或相同。

e. 扁平度和磨圆度两个形状参数的比较表明,模型颗粒与真实颗粒的形状较为相似,同时由于孔隙率和粒径级配的可控制性,所以本文建立的颗粒垫层随机重构模型基本能够还原真实的颗粒垫层,为进一步研究颗粒垫层上土工膜的顶破胀破奠定基础,也可为不规则颗粒离散元方法的建模提供参考,但本文模型只是二维随机重构模型,三维随机重构模型的构建还有待进一步的研究。