高坝泄洪消能诱发场地振动的预测方法

张陆陈,范雪梅,骆少泽,王余杰

(1.南京水利科学研究院水工水力学研究所,江苏 南京 210029; 2.南水北调东线江苏水源有限责任公司扬州分公司,江苏 扬州 225000)

泄洪消能一直是高坝建设中的关键技术难题,水流在有限的消能工内利用剪切、旋滚、摩擦、紊动消刹巨能,产生的脉动荷载容易产生流激振动。目前流激振动问题主要针对泄水建筑物自身,对于由其诱发的场地振动问题鲜有报道,但场地振动对建筑物的结构安全和人身体心理影响不容忽视。俄罗斯Zhigulevskii水电站汛期宣泄大洪水曾引起了左岸城市场地和房屋强烈振动,甚至导致大坝附近区域一些房屋开裂,附近居民出现焦虑、头晕、恶心等现象[1]。我国溪洛渡水电站曾在主汛期在坝身4个深孔开启泄洪,坝区下游右岸混凝土拌和系统的制冰楼发生明显振动[2]。2012年10月我国某水电站中孔开闸泄洪期间,下游县城部分门店卷帘门晃动，民居及校舍的门窗响动、家具颤动、吊灯摆动等,引起坝区民众不安[3]。2015年,又一座水电站下闸蓄水泄洪,同样出现了因泄洪诱发附近村庄环境振动现象。高坝泄洪消能诱发的场地振动持续时间长、影响范围广、处理难度大,是泄洪消能振动安全领域中的新难题。不同运行工况下的场地振动响应是评价振动安全、采取处理措施、制定应急预案的最基本参数,因此对泄洪消能诱发场地振动量的预测意义重大。

对于高坝泄洪消能流激振动问题,经过多年不断研究,在原型观测、模型试验、数值模拟等各个方面均取得了长足的进步[4-7],跌坎式[8]、收缩式[9]消能工的发展大幅度提升了泄水建筑物的振动安全。但场地振动有其特殊性,振源并非直接作用于场地,而是通过地层传播而来,因此其影响因素更为复杂,传播途径、地质条件、建筑物结构都对场地振动有极大影响。现场地质条件的复杂性给常用的预测模型如水弹性模型、数值模型的建立带来了极大的难度,原型观测虽可直接测量振动响应,但无法对其他不同工况进行预测预报。为此,本文依托我国某大型底流消能水电站,通过原型观测和水工模型试验有机结合的方法,分别获取“响应”和“激励”,避开准确模拟传播过程的难题,利用“响应-激励”间相关关系达到高精度预测的目标。

1 场地振动原型观测

某水电站采用射流簇底流消能方式,泄水建筑物由12个表孔和10个中孔组成,采用表中孔间隔布置形式,由中导墙分割成两个对称的消能区。

原型观测的主要目的是获取场地振动响应特性,本文重点分析其时域频域特性和幅值分布特性。场地振动传播距离远、影响范围广,因此以消力池为中心,在半径为0.5 km、1.0 km、1.5 km、2.0 km、2.5 km圆周上分别布置5个县城地基测点,共25个测点,涵盖了居民楼、学校、化工厂等重点关注位置。振动观测期间,大坝泄洪流量从6 600 m3/s逐渐减小至0。

1.1 时域频域特性

图1 地基振动速度过程线

场地振动选择低频响应灵敏的891-4型拾振器测量,配891型滤波放大器,振动信号经过放大器放大滤波后,再由动态信号采集系统采集传输至计算机存储,分析处理后得到测点的顺河向、横河向和竖直向的振动速度、振动加速度、振动位移。以振动速度为例,典型的场地振动速度时域分布特征见图1,对时域信号进行快速傅里叶变换(FFT)后频域能量分布特征见图2。由图1、图2可知,场地振动过程表现为连续型平稳随机振动并伴有冲击特征,振动能量集中在5 Hz以内,不同工况下振动主频在1.5～3.5 Hz。

图2 地基振动速度功率谱密度

1.2 幅值分布特性

典型的场地振动速度等值线分布如图3所示,整体而言,距消力池越远振动越小,但地质条件对场地影响较大,沿右坝肩向下游的原古河道的带状区域,是后期回填地基,振动明显大于其他区域,最大值相差3～5倍。在距离消力池1.5 km海拔较高的古河床位置,振动响应最大。以该点为例,泄洪流量6 600 m3/s时,顺河向、横河向及竖直向的振动加速度峰值分别为0.39 cm/s2、0.38 cm/s2、0.25 cm/s2,速度峰值分别为0.26 mm/s、0.26 mm/s、0.12 mm/s,位移峰值分别为15.95 μm、10.59 μm、6.30 μm。

图3 地基振动速度等值线分布(单位：mm/s)

泄洪流量是振动响应的直接因素,场地振动响应随着泄洪流量增大总体而言呈增大趋势,如泄洪流量从6 600 m3/s减小至330 m3/s时,振动降低约90%。但也存在流量相当而振动响应相差较大的情况,其中关键是运行方式,如2012年11月30日,上午开启左池1号、5号两中孔,开度4.5 m,泄洪流量仅960 m3/s,但民众普遍反映振动较大,振动监测表明,场地振动响应已基本达到当年6 600 m3/s泄洪流量时的水平;下午随即调整泄洪方式,增加左池2号、4号两孔,4个孔均开1.4 m,形成左池四孔局开泄流,随即感知振动变小,调整运行方式后振动显著降低,平均降幅约70%。

2 振源模型试验

高坝泄洪消能诱发的场地振动影响因素较多,如传播距离、地质条件、泄洪流量、运行方式、建筑结构等,仅通过原型观测预测振动响应,不仅难以全面考虑众多因素,且误差较大,需另辟蹊径。由于场地振动的振源为消力池脉动荷载,若直接建立振源和测点的振动响应相关关系,即可抓住问题本质,并避开准确模拟振动传播过程的难题。为此,对该水电站开展了泄水建筑物水工模型试验研究,以获取振源激励特性。

模型试验模拟了单个消能区,比尺1∶40。脉动压力测点在主消能区的底板、导墙、隔墙处均进行了加密布置,每个结构分块上测点数为2～6个,具体结构分块与测点布置情况见文献[10]。

首先对原型观测工况进行了反演,主消能区典型的脉动压力时域频域特性如图4所示。脉动压力也是平稳随机过程,频域能量集中在20 Hz以内,脉动压力主频与振动响应主频基本一致,这进一步说明振源确为水流脉动荷载。

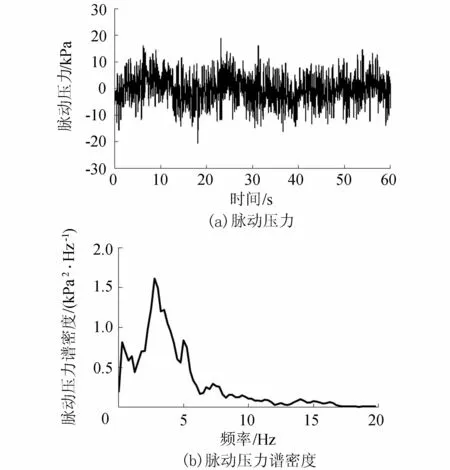
图4 典型消力池脉动压力时域及频域特性

如何选择并处理脉动压力使其成为可靠的预测参数是进行场地振动预测的关键，该预测参数不仅需考虑脉动压力的时域特征,还需考虑脉动能量分布。脉动能量是脉动压力在频域内的表现形式,由图4还可看出,由于消力池内水流流态复杂,射流、水跃、回流、旋涡等因素使脉动压力频带宽、总能量高,但对于受其激励的场地振动响应而言,贡献较大的是振动主频频段的脉动荷载,因此不宜直接采用脉动总能量作为预测参数,可通过对脉动压力进行振动主频频段的滤波处理,以此间接地将脉动能量及其分布特性反映至预测参数中,减弱了非主要因素产生的干扰,进而大大提升预测准确度。由于脉动激励荷载作用于混凝土板块上,故直接采用模型试验所测点脉动压力将带来较大的局限性,为此,本文采用经振动主频频段的滤波处理后的面脉动压力作为预测参数,综合考虑了点脉动压力和脉动能量分布的影响。

(1)

式中:Ak为第k个结构分块的总面积;m为第k个结构分块中脉动压力传感器数量;x为第k个结构分块中不同的脉动压力传感器编号;Ak-x为第k个结构分块中第x个脉动压力传感器所代表的面积。

3 “激励-响应”预测方法

通过原型观测和模型试验分别获取“响应”和“激励”后,建立两者的相关关系;然后在模型试验中测量待预测工况泄水建筑物脉动压力,计算面脉动压力,代入“激励-响应”相关关系式,进而得到待预测工况振动响应值。

3.1 “激励-响应”相关关系

以振动响应较大的古河道区域为例,各结构分块中最大的面脉动压力均方根值与振动速度相关关系如图5所示。

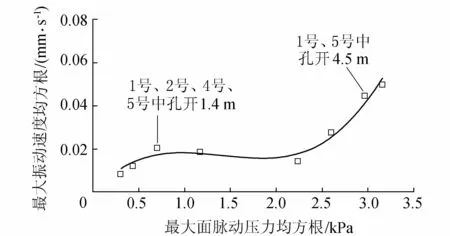
图5 典型的“激励-响应”相关关系

由图5可知,各工况下最大面脉动压力与场地振动速度均方根之间呈良好的多次方正相关关系:

v=0.082σ3-0.035σ2+0.044σ

(2)

式中:v为最大振动速度均方根,mm/s;σ为最大面脉动压力,kPa。

泄洪流量、运行方式等因素均可以在面脉动压力中得到体现,如2012年11月30日同流量不同运行方式下振幅相差较大的根本原因在于,开启左池1号、5号中孔(开度4.5 m)时最大面脉动压力是开启1号、2号、4号、5号中孔(开度1.4 m)的4倍。而对于传播距离、地质条件等因素,则可以建立多个类似式(2)的相关关系分别进行预测。

3.2 预测效果

2013年、2014年汛期古河道区域振动响应预测值与现场实测值的对比如表1所示。由表1可见,在各级泄洪流量、不同运行方式下,误差均在10%以内,预测精度较高。

表1 振动响应预测值与现场实测值的对比

采用模型试验获取脉动压力,不可避免受比尺效应的影响。赵建钧等[11]通过白鹤滩水电站1∶100、1∶80、1∶50、1∶35系列模型试验表明,随着比尺增大,脉动压力的比尺效应逐渐减小,上述前3个比尺与1∶35比尺平均相差约10%、6%、3%。本文模型比尺1∶40,点脉动压力按与真实值相差5%考虑,由于每个结构分块上测点数为2～6个,通过多点合成后,误差也随之坦化,表1中泄洪流量分别为2 100 m3/s、6 620 m3/s、8 200 m3/s、10 350 m3/s时,考虑比尺效应后最大振动速度均方根预测值与实测值误差分别为7.1%、-9.0%、9.7%及6.3%,与原误差相差不大。

4 结 论

a. 场地振动过程表现为连续型平稳随机振动并伴有冲击特征,振动能量集中在5 Hz以内,不同工况下振动主频在1.5～3.5 Hz,影响因素包括传播距离、地质条件、泄洪流量、运行方式、建筑结构等。

b. 预测所用激励荷载为板块面脉动压力,由模型试验所测点脉动压力经过主频频段滤波、合成得到,最大面脉动压力与场地振动响应呈良好的正相关关系。

c. 在各级泄洪流量、不同运行方式下,采用“激励-响应”法的振动响应预测值与现场实测值误差均在10%以内,预测精度较高。