太阳风离子在月面的反射过程及对月面电场的影响
刘沐明, 冯永勇
(1. 中国科学院 空间天气学国家重点实验室, 国家空间科学中心, 北京 100190;2. 中国科学院大学 地球与行星科学学院, 北京 100049)
月球无明显大气层和全球尺度的磁场, 直接受太阳风来流等离子体和太阳辐射的影响, 并吸收[1], 在月球背日面形成等离子体非常稀薄的区域, 称为尾流[2-3], 与水星和暴露在空间中的卫星等天体情形相似. 月面附近存在不规则磁场, 称为月表磁异常[4]. 离子在变化的磁场中运动有磁镜守恒, 因此月表磁异常可由磁镜效应[1]反射太阳风离子. 月表磁异常通过阻挡太阳风等离子体, 形成月表微磁层[5-7], 月表微磁层的形状和尺度受太阳风影响[8-9]. 由于质子和电子的质量及其回旋半径不同, 渗入微磁层的深度也不同, 因此出现了电荷分离, 该电荷分离形成的电场[10]也可能反射太阳风离子[11].
月面反射离子在行星际磁场中的运动模拟结果表明, 月面也可能反射太阳风离子[11-13]. 月面反射离子有如下可能机制: 月面向日面在太阳风等离子体的轰击及太阳紫外线的光电作用下, 达到电流平衡:
In(U)+Ii(U)+Ie(U)+Isec(U)=0,
(1)
其中:In为光电子电流;Ii为来流离子电流;Ie为流电子电流;Isec为月面受轰击产生的二次电子电流, 均为电势U的函数. 当达到电流平衡时, 月面会带有一定的电势[1,14-15]. 由于该过程受多种因素影响, 因此月球表面各处的电势不同, 并处于变化中[16]. 离子在库仑力作用下的反射, 其特性类似于光的镜面反射, 离子方向较集中, 且受月面地形的影响较小.
离子可通过与月壤的碰撞而反射. 月壤是有孔隙的土壤, 表面粗糙[17], 月面地形较复杂, 若离子通过与月壤的碰撞发生反射, 则将出现大范围散射现象[18-19]. 目前, 对太阳风离子在月表附近的反射机制尚未知. 在月面反射的太阳风离子, 会反作用于太阳风来流等离子体, 形成双流不稳定性, 加剧月球附近的等离子体波动[12]. 在太阳风中对流电场的加速作用下, 反射的等离子体做漂移运动:
VE=(E×B)/B2,
(2)
其中:E为太阳风中的大尺度对流电场;B为行星际磁场. 在月球极区附近, 回旋半径加大, 会进入月球尾流中, 对该区域的等离子体产生扰动[20]. 本文结合泰美思(THEMIS)卫星测量的空间环境数据, 对嫦娥二号卫星观测月面反射离子的运动进行反演. 统计月面反射太阳风离子的入射角和反射角, 并分析月表磁异常区反射离子的性质, 进一步探究这些离子的反射原理.
1 嫦娥二号卫星及其携带的太阳风离子探测器
嫦娥二号卫星于2010-10--2011-04绕月飞行, 采用极轨, 三轴稳定, 飞行高度100 km, 周期约2 h. 携带太阳风离子探测器(SWID). 太阳风离子探测器A机和B机具有相同的设计指标. 探测器以48个分立的能量通道接收周围离子, 这48通道的能量依次递增, 接收的离子能量为0.05~20 keV. 嫦娥二号卫星携带的太阳风离子探测器约每3 s对空间中的离子扫描一次. 图1为太阳风离子探测器的安装示意图. 由图1可见: 两个太阳风离子探测器各自被划分为12个通道, 每个探测通道占15°的扇面, 展宽6.7°, 整个探测器占一个半圆; SWID-A在卫星的yz平面内, 第一极角下沉27.3°; SWID-B在卫星的xz平面内, 第一极角下沉22.5°. 正飞期间, 嫦娥二号卫星的x轴指向卫星前进方向, 卫星的z轴指向月球[21].
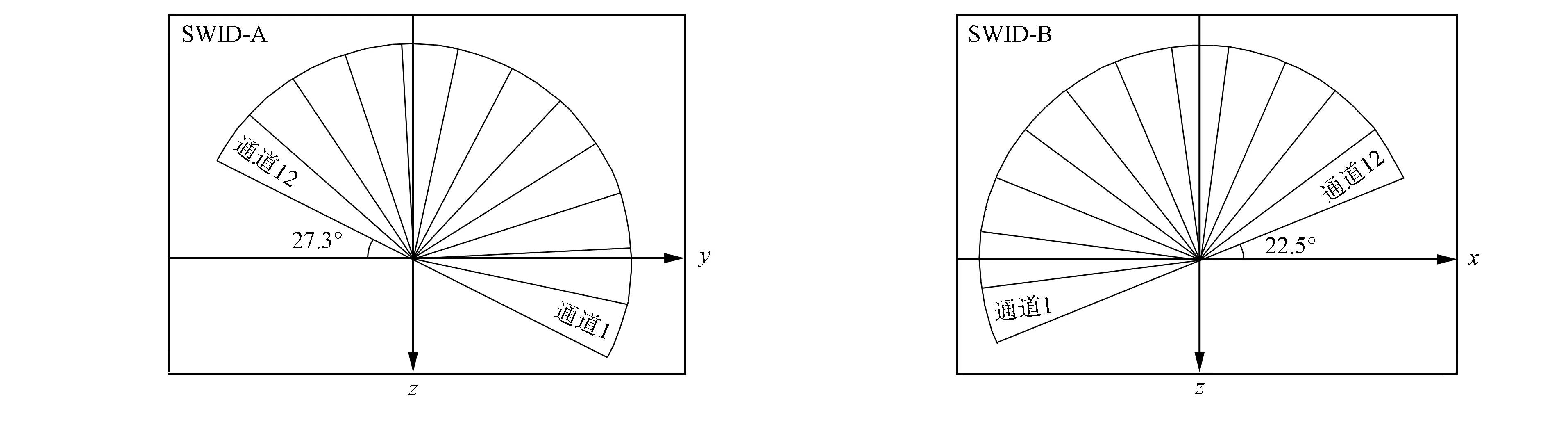
图1 太阳风离子探测器的安装示意图Fig.1 Schematic diagram of installation of solar wind ion detector
2 嫦娥二号卫星对月球空间离子的观测
嫦娥二号卫星第1060轨道(UT 2011-01-02 T 23:50--2011-01-03 T 1:50)卫星正飞期间SWID-A的1~8通道探测结果如图2所示. 此时卫星在月球向日面由南极向北极飞行, 轨道面与GSE坐标x轴交角约为30°, 行星际磁场以Bx=5 nT分量为主导, 较平静. 由图2可见, 8个探测通道的结果自上而下排列, 横轴为时间, 纵轴为离子能量. 在SWID-A的5~8探测通道中, 有一段间全部能道均充满离子能谱, 对探测器指向的计算表明, 此时探测器正对太阳, 即仪器正对太阳时探测数据受到光污染, 此外, 存在约1 keV的离子流, 这是太阳风来流离子[11]. 在1~6通道的探测数据中, 有一束通量比太阳风来流小1~2个数量级的离子流. 该离子流与太阳风来流方向不同, 来自与月面接近平行的方向. 探测到的离子分布在48个能道中, 约每3 s取样一次, 一个能道的一次取样结果称为一个离子簇. 为反演这些离子的来源, 进一步以该探测结果为基础, 通过测试粒子模拟, 反演这些离子的运动轨迹.

图2 SWID-A的1~8通道探测结果Fig.2 Detection results of SWID-A sector 1 — sector 8
3 对观测到的离子模拟溯源
在嫦娥二号卫星的探测数据中, 共有182个类似事件. 为还原这些事件中离子的运动轨迹、 位置和速度, 用测试粒子模拟的方法对离子运动进行回溯. 离子在行星际磁场和对流电场中的回旋和漂移运动表达式为
(3)
其中:m为离子质量;q为离子带电量;v为离子速度;E为对流电场;B为行星际磁场.
对第1060轨道的探测数据, 仅采用1~6通道的探测数据, 并去掉5~6通道中时间为1:15后的探测数据. 对其他事件的探测数据类似处理. 为还原事件发生时的空间环境, 采用THEMIS-B和THEMIS-C的一级数据. 由于太阳风是非常稀薄的等离子体, 因此在磁场稳定的条件下, 可用E=-v×B推算对流电场. 其中:v为太阳风流速;B为行星际磁场. 行星际磁场数据由THEMIS卫星携带的磁通门磁强计测得, 太阳风速度由静电分析器测得的离子相空间密度分布进行一次矩积分得到[22]. 由于月球与THMEIS卫星间相距1×104~2×104km, 因此THEMIS卫星测量的并非月球附近的实时电磁场. 行星际磁场冻结在太阳风粒子流中, 与太阳风一同运动, 速度为300~400 km/s. 将THEMIS卫星和月球的位置分别投影在太阳风速度的方向上, 以二者投影的距离除以太阳风速度, 可认为所得时间差即为从THEMIS卫星到月球中心的时延, 在这些事件中, 时延约为3~5 min. 由于行星际磁场位形较复杂, 且不断变化, 因此该时延方法不是对所有事件均准确. 为验证时延的准确性, 将THEMIS-B的磁场测量结果向THEMIS-C的位置做时延. 若两颗卫星的测量值吻合较好, 则认为该事件中的时延方法准确.
在其中36个事件发生时, 携带磁强计和静电分析器的THEMIS-B和THEMIS-C卫星处于太阳风中, 电磁场数据未明显缺失, 太阳风的速度和行星际磁场稳定, 且时延计算效果较好. 通过测试粒子模拟, 对36个事件中嫦娥二号卫星探测到的离子运动做反演. 选取的36个反射离子事件列于表1.
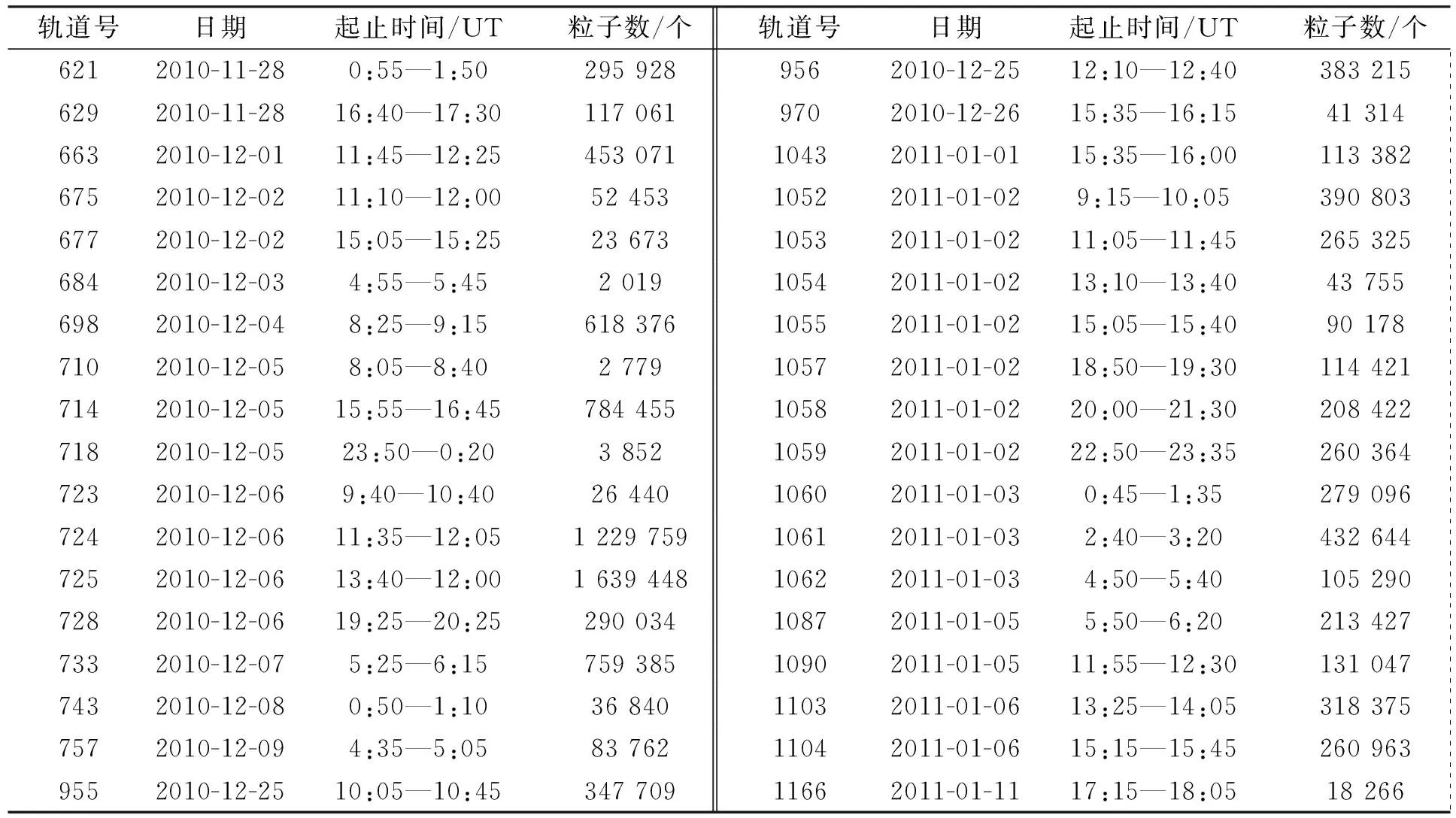
表1 选取的36个反射离子事件Table 1 Thirty-six events of selected reflected ions
在5~10 nT的行星际磁场中, 离子的回旋周期约为1~2 s. 利用测试粒子模拟反演离子运动时, 时间步长为-0.02 s(回旋周期的1/50~1/100). 嫦娥二号卫星的位置设为初始位置, 离子的初始能量和运动方向为还原SWID-A的探测结果. 各探测通道均有一定的张角, 且各能量通道有一定的能量范围. 为此, 将每个离子簇中的离子平均分布于探测通道的探测范围和能量范围中.
对下列两种情形进行模拟: 全部离子为质子, 经对离子运动反演可得这些离子来自月球表面; 全部离子为重离子, 模拟可得离子并非来自月球表面. 由于月面电离的离子以重离子为主[23], 太阳风离子以质子为主, 因此探测结果中的离子应为月面反射的太阳风离子.
设月球为一个球面, 则离子在月面反射点的法向即为该点的坐标向量(x/Rm,y/Rm,z/Rm), 其中Rm为月球半径. 离子的入射角和反射角由离子在入射和反射时离子速度方向与法线的交角给定, 即
β=(x/Rm,y/Rm,z/Rm)·(vx/v,vy/v,vz/v),
(4)
其中v为离子速率.
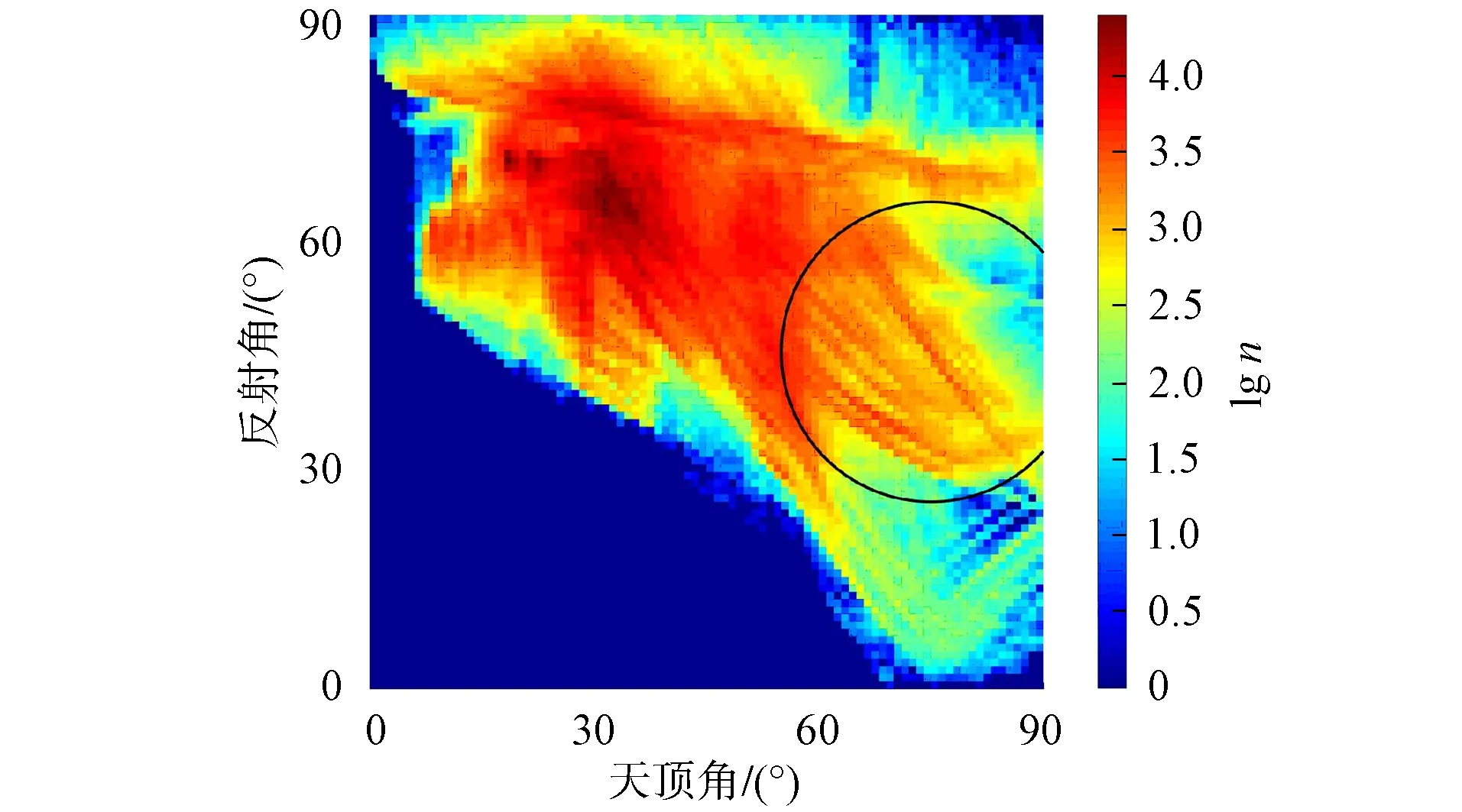
图3 离子反射点的天顶角和反射角分布Fig.3 Distribution of zenith angles and reflection angles of ion reflection points
太阳风离子流速度为300~400 km/s, 来自太阳方向, 即GSE坐标的x轴正方向, 有约10 eV量级的热运动. 若温度为1.4×105K, 此时离子有12 eV的动能, 则热运动速度约为47 km/s. 若太阳风流速为300 km/s, 则太阳风中单个离子速度可与太阳风流速有最大9°的夹角, 离子的速度方向以接近太阳风流速的方向(天顶方向)为中心, 呈一个展宽很小的分布, 即太阳风离子在月面的入射角与该处的太阳天顶角非常接近. 由于太阳风来流离子的热运动无法计算, 因此本文以反射点的太阳天顶角替代离子在月面的入射点.
通过对离子运动做反演, 可得离子在月面反射的位置及离子在该位置的速度, 以及离子反射点的天顶角, 由式(1)可计算离子的反射角. 反演结果中离子的反射点天顶角及反射角分布如图3所示. 离子的反射点与磁异常区距离较远(根据178阶球谐级数模型[4], 磁场强度小于5 nT). 其中横轴为离子在月面反射点的天顶角, 纵轴为离子在月面反射后的反射角, 不同颜色表示取某特定天顶角和反射角的离子数量. 由图3可见: 当离子在月面上时, 每个太阳天顶角值可对应大量不同的反射角值, 即离子在月面反射具有较大的随机性; 当太阳天顶角为60°~90°时(图中黑色圆圈所示), 离子的反射角与太阳天顶角呈反相关关系, 由月面上各区域离子入射位置的太阳天顶角-反射角关系可知, 该反相关关系主要出现在离子在高纬地区反射, 且行星际磁场由x分量主导的情形下. 通过几何推导, 证明该关系是由于卫星视场限制所致.
4 离子在月面上反射角-天顶角关系的几何推导
图4为离子入射点及过离子入射点的剖面示意图. 由图4(A)可见, 红线为离子入射位置的法线(即与月球球心的连线), 黑线过月心平行于GSE-x轴. 由月心向离子反射点做向量, 该向量与GSE坐标系x轴的夹角Φ即为离子反射点的天顶角. 平行于GSE坐标系的yz平面, 过离子反射点做月球截面, 可得图4(B)中的圆弧. 将离子反射点与圆弧圆心连线, 定义该连线与z轴负方向的夹角为α, 则离子在月面反射点的位置可由Φ和α确定. 卫星是极轨卫星, 在高纬地区近似卫星处于z轴负方向上. 离子由反射点P沿圆弧向卫星做回旋运动.
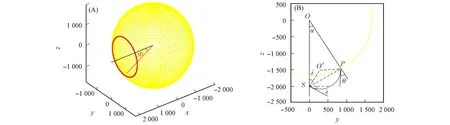
图4 离子入射点(A)及过离子入射点的剖面示意图(B)Fig.4 Schematic diagram of ion incident point (A) and cross ion incident point profile (B)
平行于yz平面, 过离子入射点做月球的切面, 可得图4(B)中的圆, 半径为
r=RmsinΦ.
(5)
在x分量主导且Bx>0的行星际磁场中, 离子的回旋面平行于yz平面, 沿图中蓝色圆弧由反射点P向卫星(记为S)回旋. 设O为截面圆心, 连结OP, 设OP与OS夹角为α, 离子在反射点附近的速度切线与OP夹角为θ.
设离子在卫星附近的速度切线与卫星y轴正方向夹角为ψ, 垂直于卫星轨道面. 离子在卫星附近速度切线与y轴正方向夹角为λ. 卫星处于坐标系高纬时, SWID-A的扇面接近GSE-yz平面,λ略小于ψ. 连接离子运动轨迹圆弧的圆心O′和卫星位置S, 则
∠OPO′=∠OPS-(∠OSP-λ),θ+∠OPO′=90°.
(6)
卫星此时在相同平面内, 即
OS=(R+100)sin(arcos(RmcosΦ)),
(7)
由三角形的正弦定理和余弦定理, 有
(8)

(9)
由三角形内角和为180°, 有
∠OPO′=∠OPS-(∠OSP-λ)=180°-2∠OSP-α+λ,
(10)
θ=90°-∠OPO′=2∠OSP+α-90°-λ.
(11)
由于月面为球面, 因此离子实际的反射角为
β=arccos(cosθsinΦ).
(12)
式(6)~(12)表明, 由于卫星携带仪器的视场限制, 因此卫星探测到的离子在月面入射点的太阳天顶角和反射角呈一种函数关系.
选取3个事件: 嫦娥二号卫星第1060轨道(UT 2011-01-03 T 0:45—1:35)、 第1061轨道(UT 2011-01-03 T 2:40—3:20)和第1103轨道(UT 2011-01-66 T 13:35—14:05), 观测月面高纬地区(纬度>60°)反射的离子. 入射点天顶角、 反射角与几何推导的拟合结果如图5所示, 其中: 在3个事件中, 蓝点表示单粒子模拟反演所得离子在月面入射点的太阳天顶角和反射角统计结果; 红线是根据式(12)拟合所得离子入射点天顶角和反射角的关系; 嫦娥二号卫星第1060,1061,1103轨道拟合的相关系数分别为0.977 0,0.973 7,0.979 3.
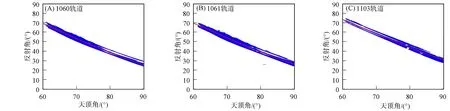
图5 入射点天顶角、 反射角与几何推导的拟合结果Fig.5 Fitting results of solar zenith angles, reflection angles and geometric deduction of incident points
5 月面静电势对离子运动的影响
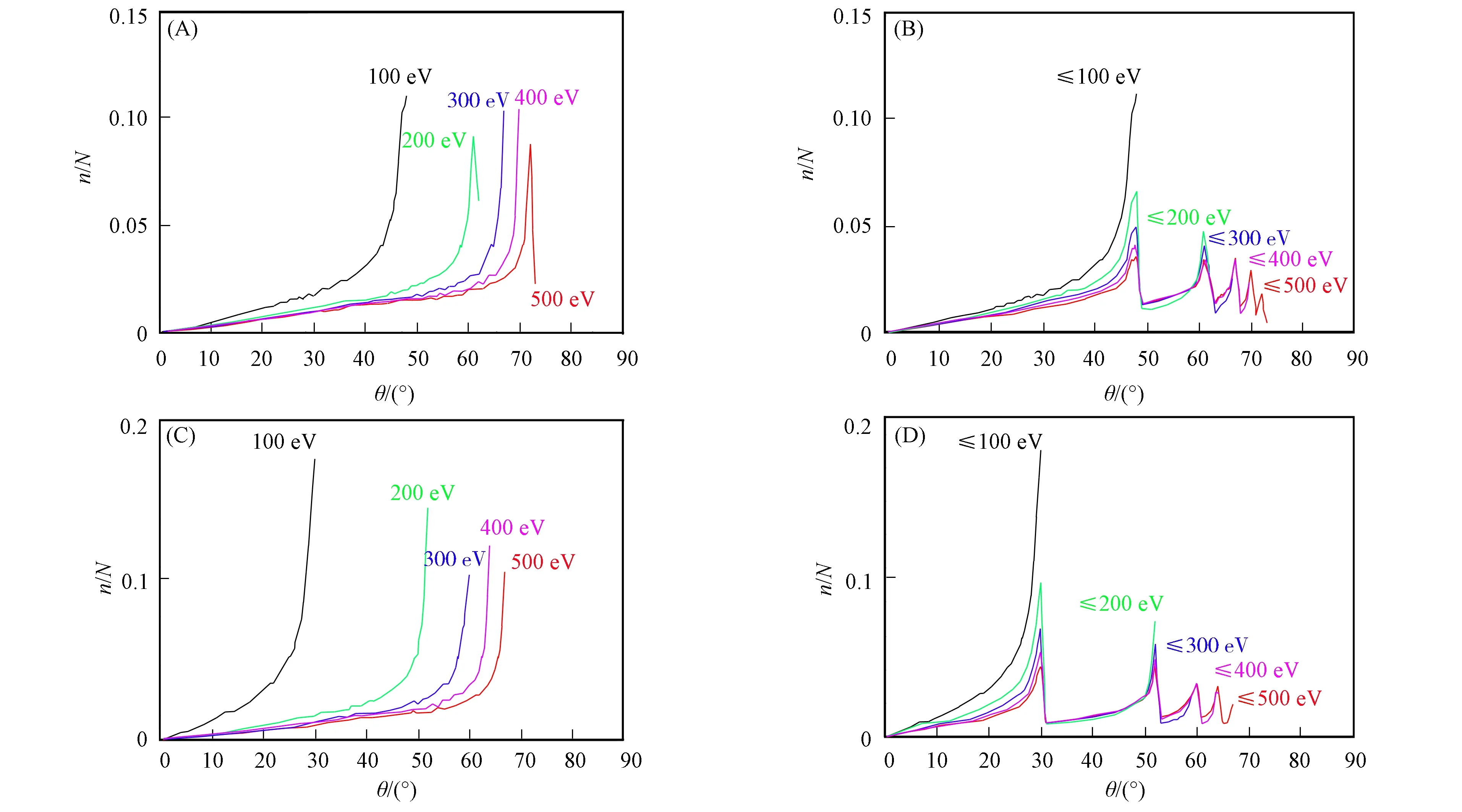
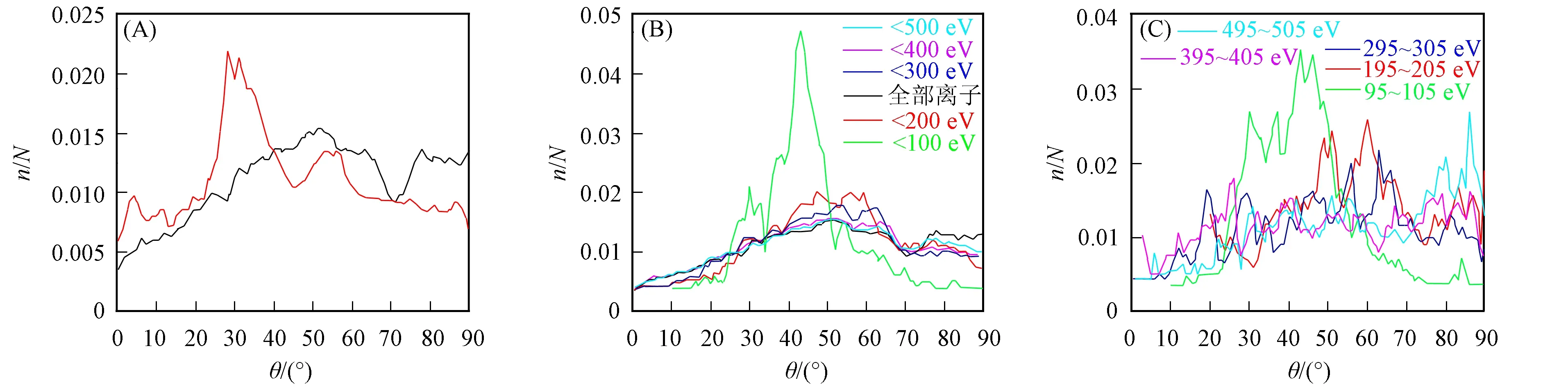
太阳风环境中Debye半径为
λD=[ε0kBTe/(nee2)]1/2,
(13)
其中:ε0为真空介电常数;kB为Boltzmann常数;Te为电子温度;ne为电子密度;e为元电荷. 对于太阳风等离子体,Te=1.4×105K,ne=5×10-6m-3,λD≈11 m. 由于等离子体在Debye半径尺度上对电场的屏蔽效应, 因此月面上的正电势在月面附近会形成较强电场, 对月面附近反射离子的运动影响较大. 但在大尺度空间可忽略对离子运动的影响. 设离子入射动能为Ek0, 出射动能为Ek, 月面电势为U, 则电场对离子加减速的能量变化为eU. 若月球向日面的eU>Ek0, 则离子将被电场反射, 形成镜面反射; 若月球向日面的eU 太阳风来流离子具有1 000 eV量级的动能, 在离子接近月面过程中, 若受10~100 V月面电场的减速作用, 则离子入射角变化较小; 若受100~1 000 V电场的减速作用, 则离子入射角变化较大. 来流离子在月壤中出现明显散射, 散射后的离子可均匀分布在各方向上, 以球面形式向外运动. 离子以反射角θ离开月面的概率正比于sinθ. 当月面具有正电势U时, 在受电场加速前, 月面反射的离子具有Ek-eU的动能, 受电场作用后, 在径向上加速, 达到动能Ek. 月面电场影响下的月面反射离子各反射角的分布如图6所示, 其中: (A)和(B)为离子在45 V月面电场影响下的反射角分布, 不同颜色表示具有不同能量的离子, (A)中离子能量分立, (B)中离子能量呈Maxwell分布; (C)和(D)为离子在75 V月面电场影响下的反射角分布, 不同颜色表示具有不同能量的离子, (C)中离子能量分立, (D)中离子能量呈Maxwell分布. 由图6可见: 月面电场越强, 对离子的收束效果越明显; 电场对能量较低的月面反射离子影响更明显; 能量较高的离子反射角较大; 在月面电场的影响下, 以球面向外扩散的月面散射离子向天顶方向集中. 对36个事件中10 437 331个离子(36个离子事件中的离子数目见表1)的反射角和反射点天顶角的统计结果如图7(A)所示, 其中: 横轴为离子的天顶角和反射角; 纵轴为天顶角和反射角对应的概率密度(离子数/离子簇数, 并进行归一化, 0~90°积分结果为1); 红线为离子入射点的天顶角分布; 黑线为离子的反射角分布. 由图7(A)可见: 离子反射的天顶角具有明显峰值, 实际离子入射角可能会出现约9°的展宽, 但仍会出现明显峰值; 离子反射角分布平缓, 更接近平均分布. 即月壤对离子有明显的散射作用. 对能量低于一定值的月面反射离子取各反射角的概率密度(离子数/离子簇数)统计结果如图7(B)所示. 由图7(B)可见, 月面电场对能量低于100 eV的离子, 收束效果明显, 在40°~50°出现峰值, 即月面有45~55 V电势. 特定能量离子的反射角分布如图7(C)所示. 由图7(C)可见: 具有更高能量离子反射角概率密度的峰值出现在反射角更大的区域, 约为100 eV离子的反射角分布出现两个峰值, 在30°附近符合75 V月面电势特征, 在45°附近符合45 V月面电势特征; 200 eV离子的反射角分布出现两个峰值, 在50°和60°附近, 分别符合75 V和45 V月面电势特征; 具有较高能量的离子, 在较大角度出现反射角峰值. 图6 月面电场影响下的月面反射离子各反射角的分布Fig.6 Distribution of ion reflection angles under influence of lunar surface electric field 图7 离子天顶角和反射角的分布Fig.7 Distribution of ion zenith angles and reflection angles 综上, 本文用测试粒子模拟的方法, 对月面反射太阳风离子的运动进行了反演. 通过对反演得到离子的入射角和反射角统计结果表明: 离子与月壤碰撞, 受大范围、 无规则散射, 并受月面电场向天顶方向的加速; 月面电势约为45~75 V.