游离亚硝酸抑制硝化杆菌属(Nitrobacter)活性动力学研究
孙洪伟,于 雪,李维维,祁国平,马 娟,陈永志,吕心涛
游离亚硝酸抑制硝化杆菌属()活性动力学研究
孙洪伟1,2*,于 雪1,2,李维维3,祁国平3,马 娟1,2,陈永志1,2,吕心涛4
(1.兰州交通大学环境与市政工程学院,甘肃 兰州 730070;2.甘肃省污水处理行业技术中心,甘肃 兰州 730070;3.甘肃省轻工研究院,甘肃 兰州 730070;4.北京城市排水集团有限责任公司科技研发中心,北京 100032)
为探究游离亚硝酸(FNA)对亚硝酸盐氧化细菌中硝化杆菌属()活性抑制动力学影响,采用序批式活性污泥(SBR)反应器,在通过改变系统进水FNA浓度达到富集基础上,以富含污泥为对象(宏基因组物种注释和丰度分析显示上占细菌总数40.3%),基于批次试验,考察不同FNA浓度梯度下亚硝酸盐氧化过程比亚硝态氮氧化速率(SNiOR)变化规律,进而拟合FNA抑制活性抑制动力学模型,并进行统计学分析.结果表明,当FNA≤0.1mg/L时,随着FNA浓度升高,SNiOR迅速升高.当FNA>0.1mg/L时,SNiOR随着FNA浓度升高而降低.尤其当FNA浓度高于0.7mg/L时,SNiOR始终维持在0gN/(gVSS·d),表明活性统被完全抑制.统计学分析结果显示相对于Haldane、Aiba、Edwards-1#、Edwards-2#、Luong抑制动力学模型,Han-Levenspiel模型最适合描述FNA对活性的抑制影响.其统计学常数:残差平方和(RSS)为0.02、可决系数(2)为0.90、拟合方程的方差检验统计量值为78.1、可信度值为3.29×10-12,其动力学常数值分别为:最大比亚硝态氮氧化速率(max)为1.57gN/(gVSS·d);半饱和常数(S)为0.01mg/L;临界抑制常数(m)为0.66mg/L.
游离亚硝酸;硝化杆菌;比亚硝态氮氧化速率;抑制动力学;宏基因组
在废水生物脱氮系统中,氨氧化菌(AOB)和亚硝酸盐氧化菌(NOB)以协同作用共存,完成氨氮(NH4+-N)向硝态氮(NO3--N)转化,AOB将NH4+-N氧化为亚硝态氮(NO2--N),NOB将NO2--N进一步氧化为NO3--N.NOB主要是由4类菌属构成:硝化杆菌属(),硝化球菌属(),硝化刺菌属()和硝化螺菌门()[1].研究表明,和是污水处理系统中最为常见NOB菌属[2],其中在高底物浓度、高溶解氧条件下含量远高于[3-4].大多研究者认为,硝化反应过程中游离氨(FA)和亚硝酸根(NO2-)的质子化产物游离亚硝酸(FNA)对NOB存在一定的抑制作用[5-6].Anthonisen等[7]研究认为FNA是抑制NOB活性的主要因素之一,一定浓度的FNA对NOB活性具有强烈的抑制作用.Ma等[8]对富含NaNO2的模拟废水富集NOB发现,当FNA= 0.25mg/L时,NOB活性降低65%.Wang等[9]发现当FNA=0.24mg/L时,可完全抑制富含NOB的活性污泥.Katsou等[10]处理有机物发酵液和城市污水混合液时发现,当FA浓度介于0.19~1.52mg/L时NOB活性降低35~65%.
生化反应动力学最直接地体现基质降解速率和反应物生成速率的变化关系,进而描述微生物活性.因此,通过抑制动力学模型,可清楚反应微生物受基质抑制情况.一些文献对比了几种不同的基质抑制动力学模型.如:Tanyolac等[11]通过非线性拟合对比分析了几种抑制动力学模型,最终发现Edwards[12]模型能够较好描述硫酸铵对废水好氧生物处理过程中微生物的抑制作用.目前,大多研究集中于FNA对短程硝化污泥动力学研究[11-16],而较少的文献从数理统计学方面评价不同动力学模型描述FNA抑制活性的适宜程度.
因此,本试验在实现富集基础上,基于动力学抑制模型,考察FNA对活性的抑制影响,进而对比统计学结果,获得最优抑制动力学模型和动力学常数值,以指导生物脱氮技术在理论研究及实际工程中的应用.
1 生化反应抑制动力学模型
目前表征FNA抑制NOB活性动力学模型主要包括以下5种.
(1)Haldane模型
为通过动力学形式解释微生物利用具有抑制性功能的底物,1968年,Andrews[17]提出底物浓度对比增长速率的影响可以通过式(1)表示.该模型是在1930年Haldane[18]认为酶和底物形成带有两个底物分子的惰性酶-底物复合物,该复合物对酶产生抑制作用的基础上推导得出[19-20].
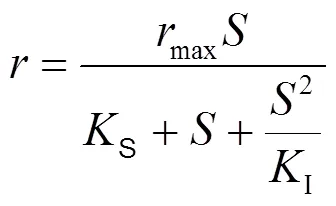
式中:为底物浓度(mg/L);为底物的比降解速(d-1);max为微生物未被抑制时的最大比降解速率(d-1);S为饱和常数,数值上等同于微生物未被底物抑制时底物最大比降解速率一半所对应的最小底物浓度(mg/L);I为抑制常数,数值上等同于微生物被底物抑制时底物最大比降解速率一半所对应的最大底物浓度(mg/L).
(2)Aiba模型
1968年,Aiba等[21]研究酒精发酵生化反应过程中,发现了发酵产物(酒精)对生化反应具有抑制作用,提出产物抑制理论和抑制模型,如式(2)所示.
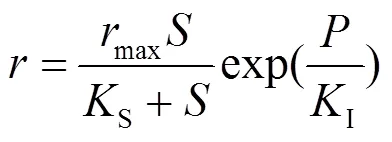
式中:为产物浓度(mg/L);I为抑制常数;式中其余符号定义见Haldane模型,本文不再赘述,下同.
1970年,Edwards[12]认为Aiba提出产物抑制的指数关系同样可用来描述相关底物抑制,因此,Edwards将式(2)修正为式(3),文献[9]仍将该模型称为Aiba模型.
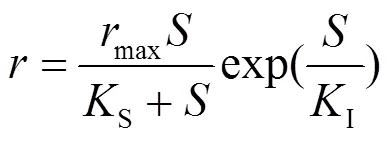
(3)Edwards-1#模型
1970年,Edwards[12]提出公式(4)用于描述基质底物对生化反应的抑制关系.该方程是基于高浓度葡萄糖和半乳糖的抑制动力学和Haldane[18]对惰性酶底物复合物假设研究基础上提出来的.为区分两个Edwards模型,故将该模型命名为Edwards-1#,下同.

式中:为抑制常数.
(4)Edwards-2#模型
1942年,Teissier[22]通过研究底物浓度对微生物比增长速率的影响提出式(5),该公式描述了底物浓度对细菌增长具有刺激作用.
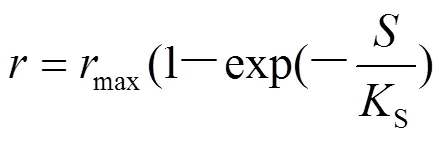
1970年,Edwards将Teissier假设与高浓度底物抑制作用相结合,建立了Edwards-2#模型,如式(6)所示.

(5)Luong模型
1987年,Luong[23]在研究丁醇作为基质底物对酵母菌生长过程的抑制作用基础上,建立了Luong基质抑制模型,该模型被广泛用于描述基质浓度对微生物生长过程的影响,其表达式如公式(7)所示:
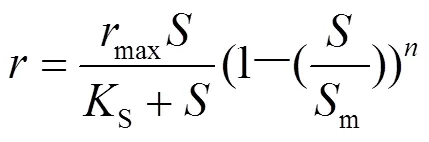
式中:m为微生物的净生长速率停止时的底物浓度(mg/L);为Long系数;
(6)Han-levenspiel模型
1988年,Keehyun Han与Octave Levenspie[24]在Monod模型基础上共同提出了Han-levenspiel模型,该模型认为在高浓度底物浓度条件下,微生物活性被完全抑制,微生物停止增长,其表达式如公式(8)所示:

式中:,均为常数,其取值与基质对微生物抑制类型有关;
2 材料与方法
2.1 试验装置及运行方式
本试验采用有效容积为7L(富集阶段)和3L(FNA抑制批次试验阶段)的SBR1和SBR2两种类型反应器. SBR1运行方式:瞬时进水(1min),硝化(通过在线监测DO值实时控制硝化终点),静置沉淀(30min),排水(5min).第2阶段试验采用有效容积为3L的SBR反应器. SBR2运行方式:瞬时进水(1min),硝化(硝化时间为8h),静置沉淀(30min),排水(5min).
2.2 试验用水、接种污泥及水质分析项目
试验用水采用人工模拟废水,其水质特性见表1.原水采用去离子水,进水NO2--N通过投加NaNO2溶液实现,初始pH值通过1mol/L盐酸(HCl)溶液和1mol/L氢氧化钠(NaOH)溶液调节.其他成分如下:0.4gNaHCO3,0.9g KH2PO4,1.2g K2HPO4,以及0.9mL微量元素,每升微量元素中含有: 1.25gEDTA, 0.55gZnSO4•7H2O, 0.4gCoCl2•6H2O, 1.275gMnCl2• 4H2O, 0.4gCuSO4•4H2O, 0.05gNa2MoO4•2H2O, 1.375gCaCl2• 2H2O, 1.25gFeCl3•6H2O, 44.4gMgSO4• 7H2O.此外,硝化过程中DO控制在4~4.5mg/L,采用加热棒控制反应器内混合液温度.
第1阶段试验采用的污泥取自兰州市西固区兰炼污水处理厂氧化沟好氧段污泥,具有良好生物脱氮性能,初始混合液挥发性悬浮固体浓度(MLVSS)为3323mg/L.第2阶段试验以第1阶段中已富含NOB的活性污泥为研究对象,MLVSS为(1485±35) mg/L.
NO2--N、NO3--N、混合液悬浮固体浓度(MLSS)及MLVSS均采用国家规定的标准方法[25];pH值、DO和温度通过WTW-Multi3420实时监测;活性污泥经过预处理后采用扫描电子显微镜(Scanning Electron Microscope, SEM)进行观察.
宏基因组物种注释和丰度分析:①污泥样品的Scaffolds/Scaftigs序列与NCBI-NT数据库中的细菌、古菌、真菌和病毒序列进行BLASTN比对(E值设定为<0.001).②通过MEGAN[26]软件中采取“最低共同祖先”算法[27]将参考序列分为不同物种分枝前的最后一级共同分类,作为目标序列的物种分类注释信息.③结合Saffolds/Scaftigs序列在各样本中的丰度数据,获得各样本在各个分类等级上的相对丰度分布表.
废水中FNA浓度是NO2--N浓度、温度和pH值三者的函数,其关系为(式9):
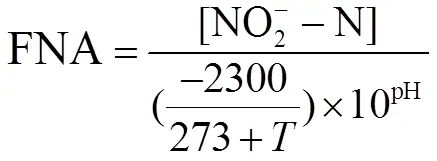
式中:[NO2--N]为NO2--N浓度;为温度;pH为溶液pH值.
2.3 试验方案
试验共运行446个周期,根据不同的运行状况可分为两个阶段.第1阶段试验(1~419周期)——富集.本阶段试验通过梯度增加进水NO2--N浓度实现的快速富集,具体运行条件见表1.
第2阶段试验(420~446周期)——FNA对抑制动力学研究.本阶段试验以第1阶段中富含的活性污泥为研究对象,通过设定不同NO2--N浓度、pH值和温度,以获得不同FNA浓度,通过批次试验,考察不同FNA浓度梯度下,FNA对活性的影响.具体运行条件见表2.并通过上述6种抑制动力学模型进行描述,最终建立FNA浓度对活性抑制动力学模型.

表1 NOB富集过程运行条件
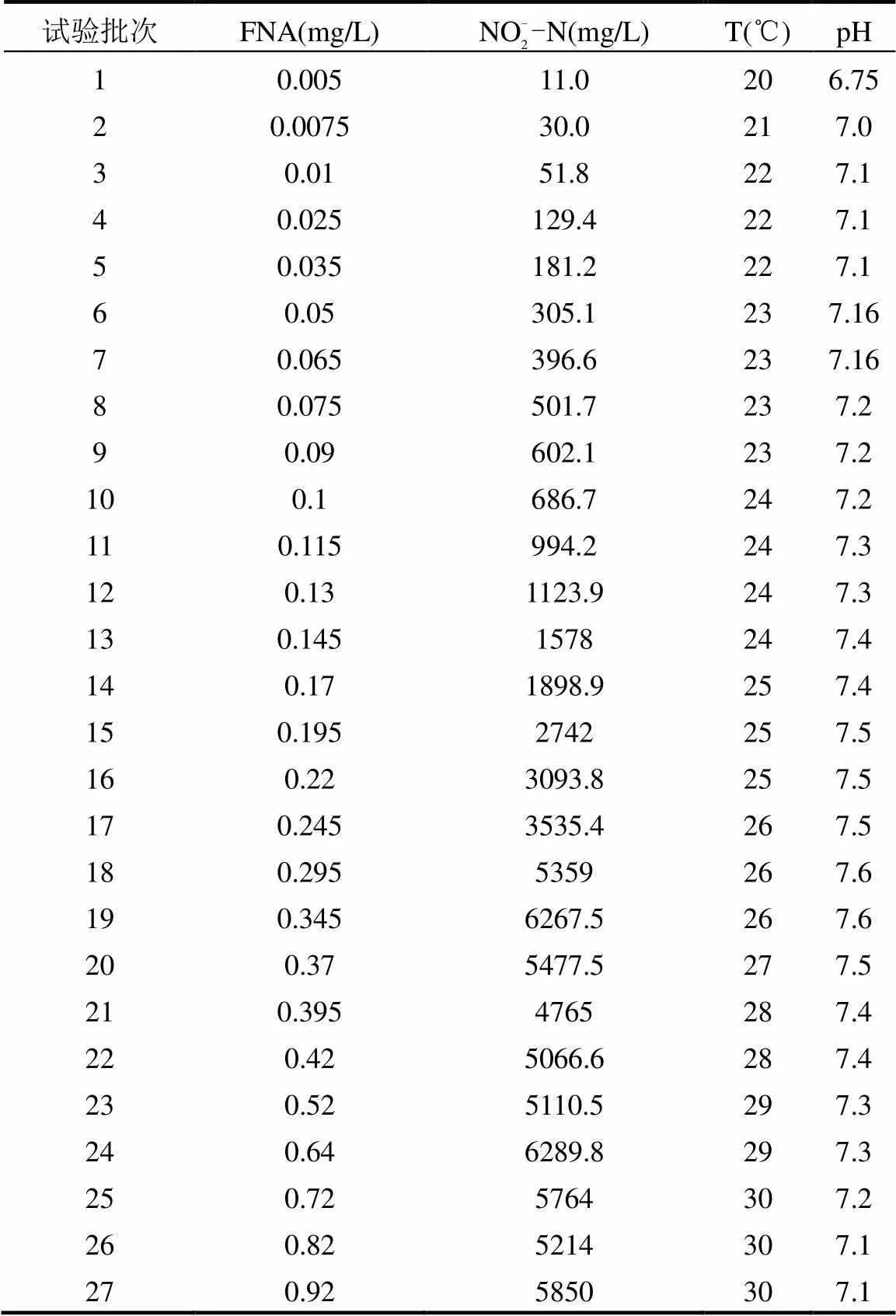
表2 批次试验条件
3 结果与讨论
3.1 Nitrobacter的富集培养
图1为富集阶段SBR系统硝化开始、结束时NO2--N浓度、亚硝态氮氧化速率(NiOR)以及NO2--N去除率的变化规律.试验运行过程中,进水NO2--N浓度从10mg/L梯度升高到700mg/L.可以看出,硝化结束时NO2--N浓度均低于5mg/L,平均值为2.07mg/L,整个试验周期NO2--N去除率均达到98%以上,系统具有良好的脱氮性能.此外,由于进水NO2--N浓度的增加,NiOR逐渐增加[0.32mg/ (L·min)→1.93mg/(L·min)],呈正相关.当NO2--N³700mg/L时,NiOR始终维持在1.80mg/(L·min)以上,表明SBR系统具有良好的亚硝酸盐氧化性能.
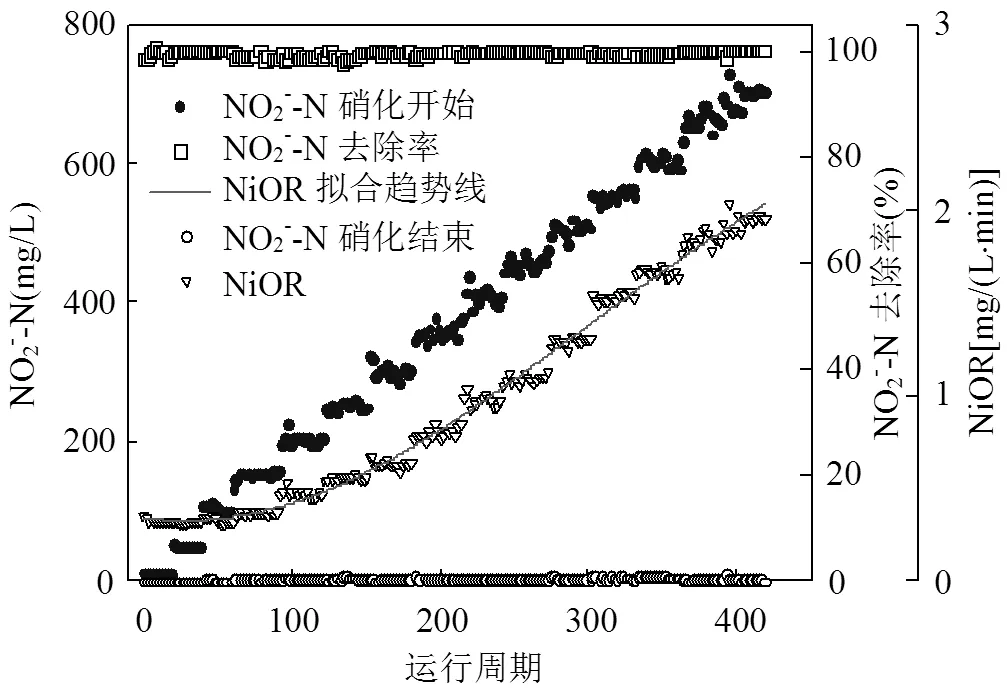
图1 Nitrobacter富集培养阶段SBR系统硝化性能
对微生物16S rRNA基因的特定区域进行靶向测序,获得SBR系统内微生物群落的具体组成结构(图2).通过Origin9.0软件,对各样本中的优势物种(取总体丰度前30位物种)在属水平上分析并绘制柱状图.分析发现:各平行样在属水平上微生物类型基本相同,其中平均相对丰度为40.3%.此外,基因测序结果显示其余菌属在污泥微生物群落中占比均低于5%,表明经过富集培养后SBR系统污泥微生物中占绝对优势地位.
为了更深入观察富集后形态特征,采用扫描电镜(SEM)观察活性污泥菌属细胞表面形态(图3).结果表明, 富集后污泥形态规则,边界清晰,呈颗粒状.活性污泥系统中以杆状菌及梨状菌属为主[(0.5~0.8)´(1.0~2.0)],符合文献[28]中关于形态与大小描述.
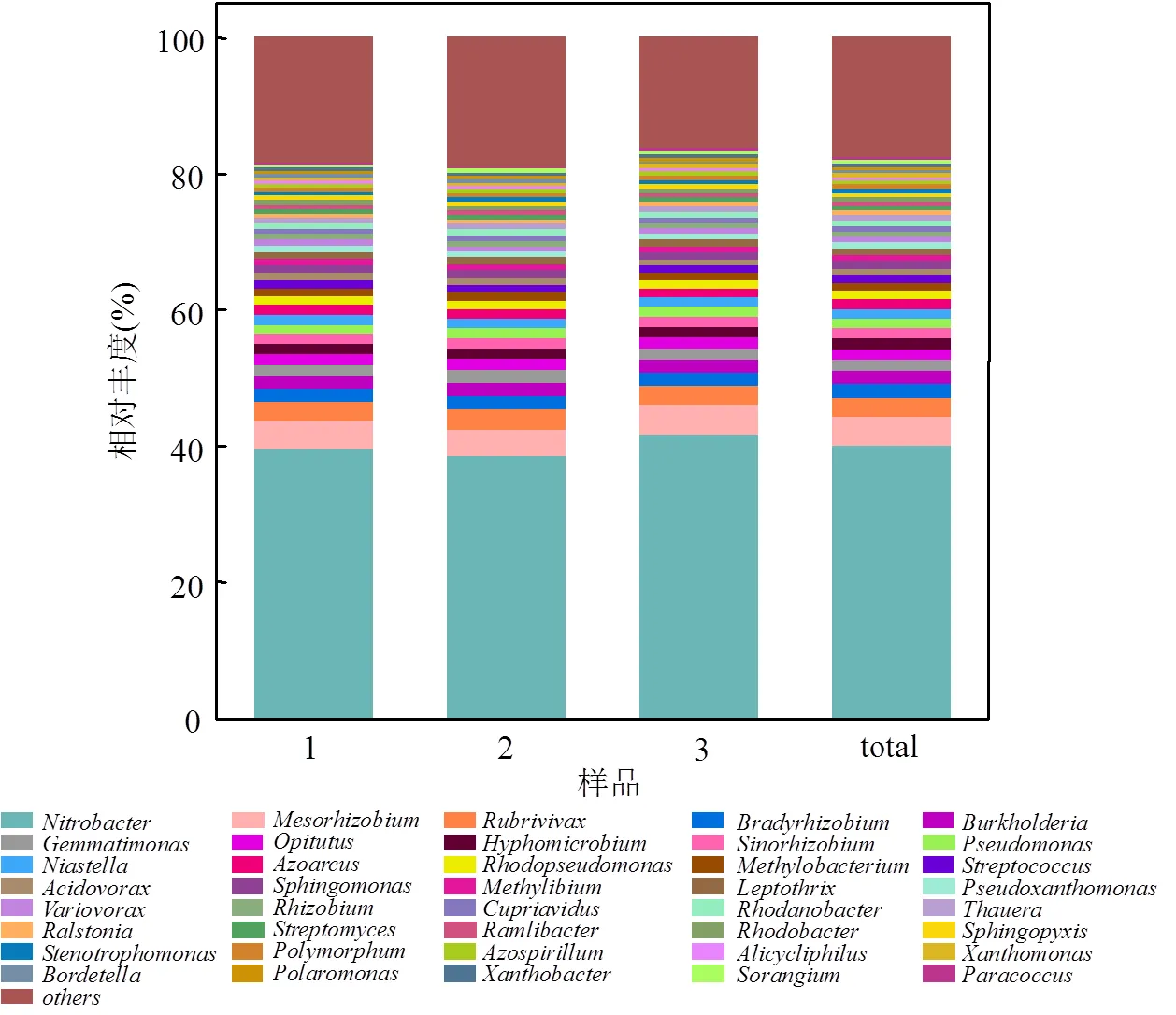
图2 SBR系统微生物群落组成结构

图3 Nitrobacter富集成功后SEM图
3.2 FNA对Nitrobacter氧化性能影响
图4为不同FNA浓度条件下硝化反应开始、结束时NO2--N浓度,转化率及其氧化量的变化规律.试验过程中,通过改变进水NO2--N浓度、温度以及pH值来提高FNA浓度.随着运行周期的增加,进水FNA浓度逐渐增加,硝化反应开始和结束时NO2--N浓度均呈现增加的趋势.这是由于相同硝化反应时间内随着进水NO2--N浓度增加导致曝气结束时NO2--N未反应完全.此外,当FNA£0.1mg/L时, NO2--N转化率均维持在99%以上,同时NO2--N氧化量达到最大,为709.4mg/L.当FNA>0.1mg/L时,NO2--N转化率及其氧化量逐渐下降,表明FNA对的活性开始产生抑制作用.张宇坤等[29]研究表明,当FNA=0.01mg/L时NOB活性逐渐降低.分析原因:NOB生长环境及其污泥浓度均可影响NOB活性,本试验经过富集培养后占活性污泥菌群比例较高,因此采用此类活性污泥进行FNA对抑制影响动力学研究,更具有代表性.
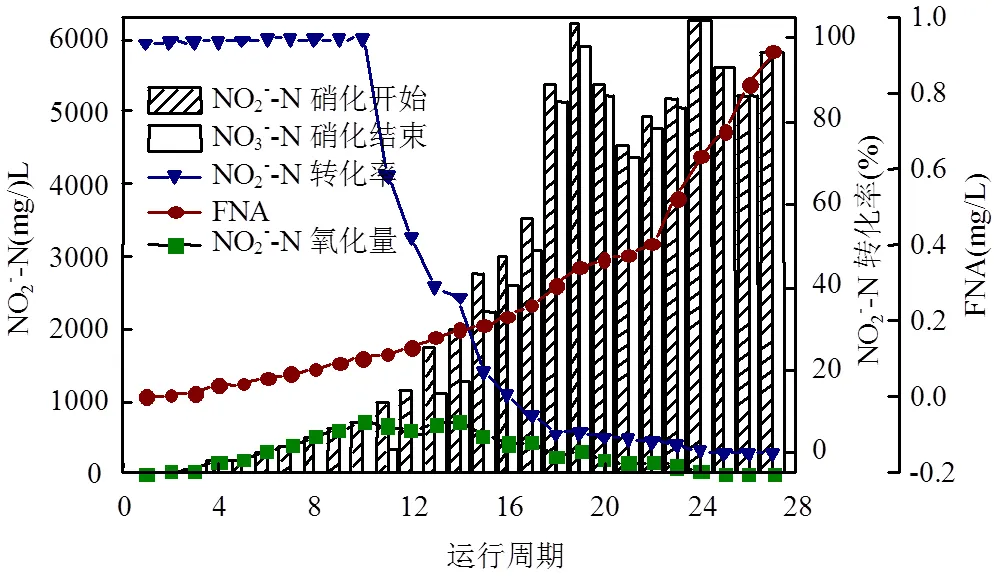
图4 不同FNA条件下系统内NO- 2-N去除性能
3.3 FNA抑制Nitrobacter活性动力学
为了更好地描述FNA对活性的抑制影响,采用上述6种抑制动力学模型对试验数据进行拟合,拟合结果如图5所示.6种动力学模型均呈现出先增加后降低的趋势,故均可用于描述FNA对活性的抑制影响.当FNA<0.18mg/L,随着FNA浓度的增加,SNiOR急剧增加,表明在此FNA浓度范围内, FNA对活性具有促进作用.当FNA浓度介于0.19~0.64mg/L之间时,SNiOR呈现降低的趋势,表明FNA对活性产生显著抑制作用,活性逐渐降低.当FNA³0.7mg/L时,SNiOR为零,完全失活.
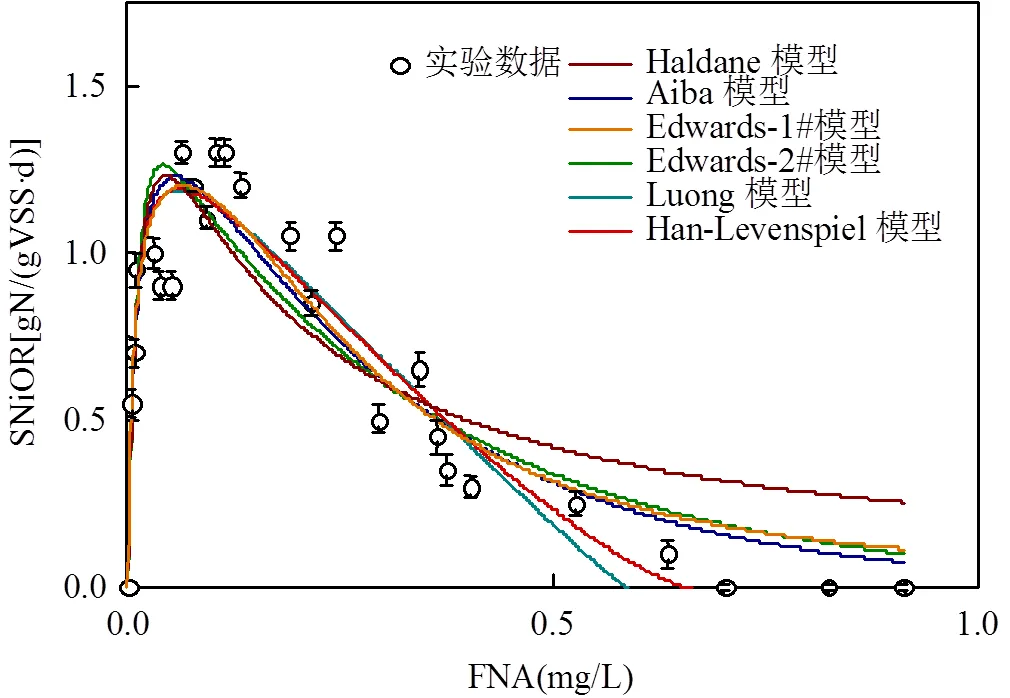
图5 FNA对Nitrobacter活性抑制动力学拟合
为了更精确的比较6种动力学模型对试验数据的拟合效果,基于统计学理论,对6种模型的动力学参数和拟合效果进行分析,选择最适宜的动力学模型描述FNA对活性的影响.分析统计结果见表3.
基于统计学中方差分析对动力学参数值进行对比分析发现,Edwards-1#模型获得的拟合结果不收敛,拟合失败,因此,Edwards-1#模型不能用来描述FNA对NOB活性的影响.通过残差平方和(RSS)与相关系数(2)对比分析,RSS和2均可描述试验数据与拟合曲线的接近程度,RSS越小,拟合效果越好.2越大,试验数据在拟合曲线附近越密集,曲线拟合程度越高.相对于Haldane模型,Aiba模型、Edwards-2#模型以及Luong和Han-Levenspiel模型的RSS较小,2较大,因此,Aiba模型、Edwards-2#模型、Luong以及Han-Levenspiel模型更适宜描述FNA对活性的抑制影响.基于方差分析,值与值均能够预测自变量与因变量的关联程度.值是回归方程的显著性检验,值表示试验结果可信度,值越大,值越小,可表明自变量和因变量显著相关,方程拟合度越好,且当<0.05时,自变量可用于预测因变量.5种模型拟合得到的值均小于0.001,但Han-Levenspiel模型值最小,值最大.因此,综合RSS、2、值和值考虑,Han-Levenspiel模型描述FNA对活性抑制作用是最优的.
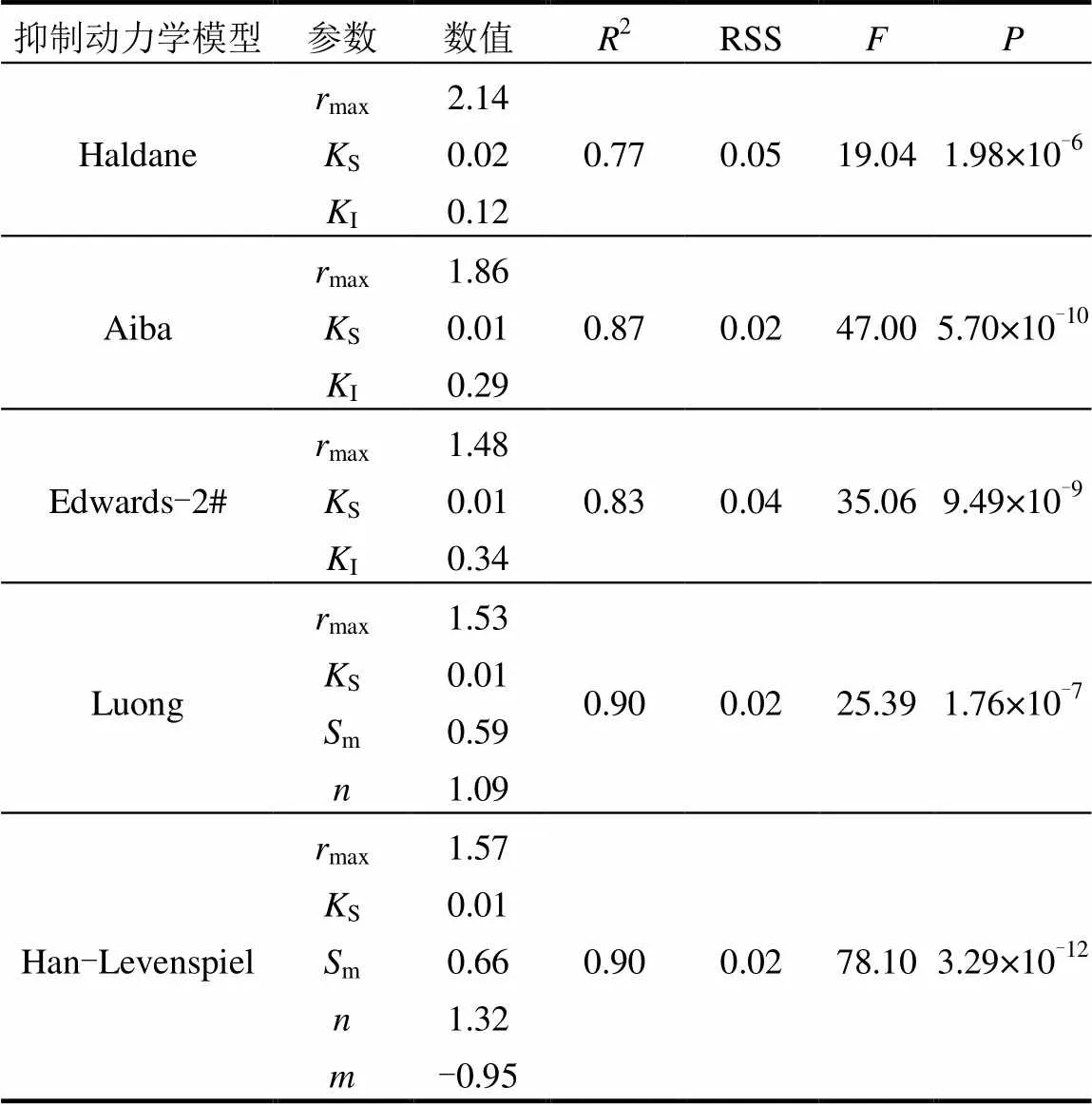
表3 5种抑制动力学模型参数以及统计学分析
3.4 关于FNA和NO2--N谁是Nitrobacter真正抑制剂的探讨
1976年,Anthonisen等[7]研究表明,FNA对NOB的抑制阈值为0.2~2.8mg/L.此后,众多学者关于FNA和NO2--N谁是NOB菌属的真正抑制剂及其抑制浓度范围进行了研究,但试验结果和NOB真正抑制剂研究目前尚未达成共识.表4总结了现有文献和本试验关于FNA和NO2--N对NOB活性影响的研究现状.Park等[13]基于抑制动力学模型研究亚硝酸盐氧化抑制动力学发现,当pH值由8降为7时,q/qmax(比NO2--N利用速率/比NO2--N最大利用速率)显著降低,表明pH值对NOB活性产生影响,认为FNA是NOB真正抑制剂.Vadivelu等[30]通过改变进水NO2--N浓度对比耗氧速率(SOUR)影响研究含73%活性污泥时发现,FNA抑制活性.Carrera等[31]对悬浮生物系统和附着型生物系统硝化过程研究发现,在恒定pH值和温度条件下,高浓度NO2--N对NOB活性产生抑制作用,计算可得在该NO2--N浓度条件下FNA= 0.02mg/L,并未达到FNA抑制NOB浓度阈值[7].因此,认为NO2--N对NOB活性产生抑制作用.
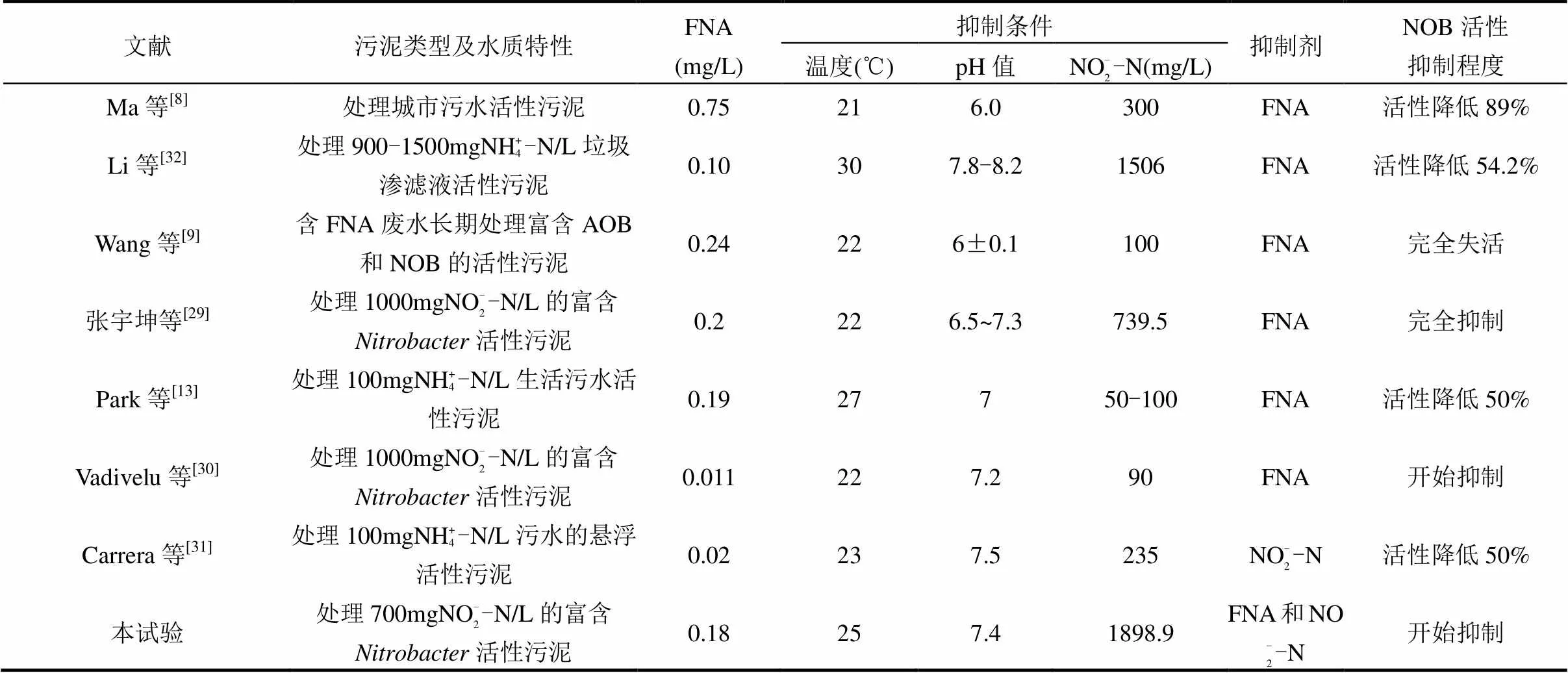
表4 关于FNA和NO2--N抑制NOB文献资料报道
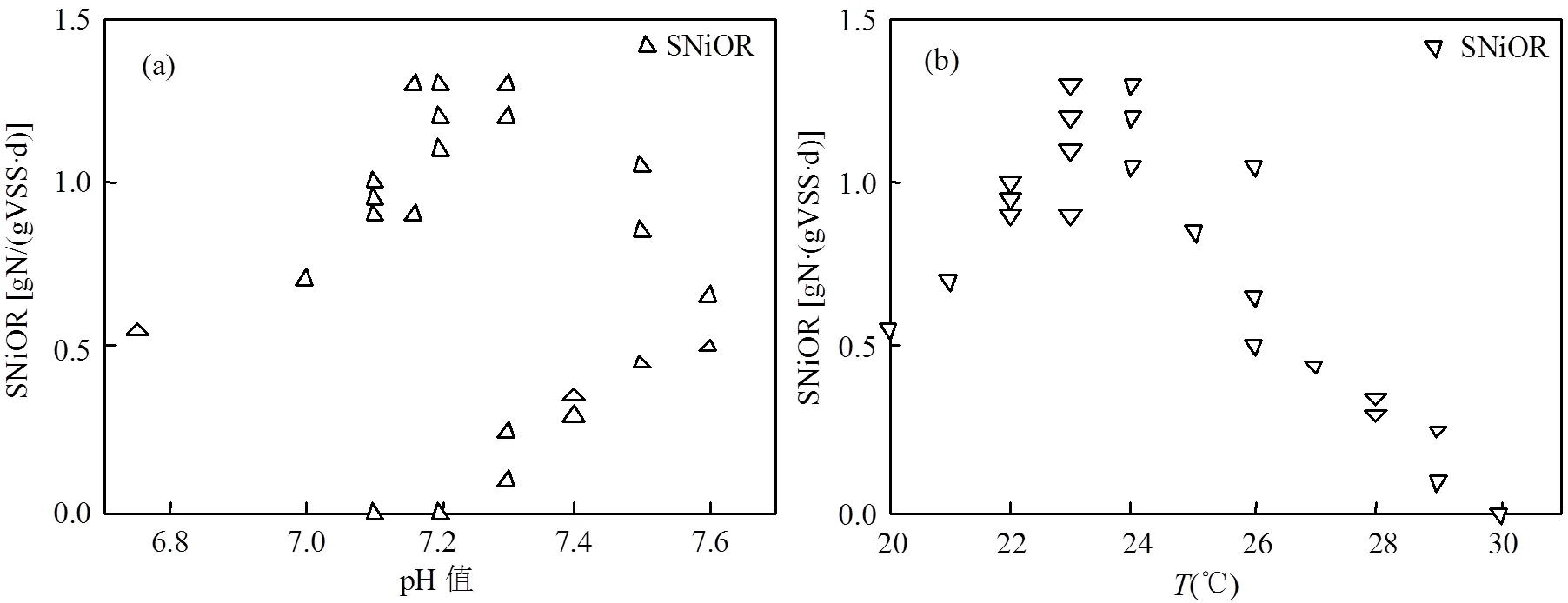
图6为本试验pH值、、NO2--N和FNA浓度分别对活性的影响.由图可知,不同pH值、、NO2--N和FNA浓度均对活性有影响.本试验控制的pH值和条件下,pH和对活性产生一定的影响,在pH值为7.2左右,为24℃时活性最强[图6(a,b)].此外,基于Han-Levenspiel抑制动力学模型,由图6(c,d)可知,以FNA和NO2--N为抑制剂时, SNiOR拟合曲线均呈先升高后降低的趋势,表明高浓度NO2--N和FNA对均产生抑制作用.因此,两者均可抑制的活性.当以NO2--N为抑制剂时,NO2--N浓度较高时,SNiOR出现明显波动,可决系数2较低,仅为0.76,曲线拟合程度较低.而以FNA为抑制剂时,SNiOR拟合曲线数据点在拟合曲线附近较紧密,2为0.90,曲线拟合程度较好.试验表明,一定pH值和及高浓度NO2--N和FNA对均具有抑制作用,由于FNA为pH值、和NO2--N三者的函数,也就是说FNA综合了NO2--N浓度、pH值和对活性的影响.在任何一个污水生物脱氮处理系统中,NO2--N,pH值和是客观存在的基质和环境条件.因此,FNA作为抑制剂时能够更加全面的反映NO2--N,pH值和三因素对活性的抑制作用,也可采用抑制动力学方程来描述.因此,相比于单一NO2--N浓度对活性的抑制影响,FNA对活性的抑制模型具有更好的实际应用价值.
4 结论
4.1 控制DO³4mg/L,=25℃条件下,以NaNO2为唯一能源,通过梯度提高NO- 2-N浓度可实现的富集,经过419个周期,宏基因组物种注释和丰度分析显示占细菌总数40.3%,成为优势菌种.
4.2 当FNA>0.1mg/L时,NO- 2-N转化率及其氧化量逐渐下降,表明FNA对活性开始产生抑制作用,当FNA=0.7mg/L时,被完全抑制.
4.3 基于对Haldane、Aiba、Edwards-2#、Lunog和Han-Levenspiel抑制动力学模型的统计学分析发现,Han-Levenspiel模型能够较好的描述FNA对抑制影响.
4.4 基于Han-Levenspiel模型对FNA与NO- 2-N分别作为抑制剂进行拟合分析发现,通过FNA大小表征抑制程度具有更好的实际意义.
[1] Stackebrandt E, Goebel B M. Taxonomic note: a place for DNA-DNA reassociation and 16S rRNA sequence analysis in the present species definition in bacteriology [J]. Internation Journal of Systematic Bacteriology, 1994,44(4):846-849.
[2] Peng Y, Zhu G. Biological nitrogen removal with nitrification and denitrification via nitrite pathway [J]. Applied Microbiology and Biotechnology, 2006,73(1):15-26.
[3] 包 鹏,王淑莹,马 斌,等.不同溶解氧间歇曝气对亚硝酸盐氧化菌的影响 [J]. 中国环境科学, 2016,36(9):2696-2702.
[4] 马琳娜,刘文龙,张 琼,等.游离亚硝酸(FNA)对A2O污泥菌群结构的影响 [J]. 中国环境科学, 2017,37(7):2566-2573.
[5] Zhou Y, Oehmen A, Lim M, et al. The role of nitrite and free nitrous acid (FNA) in wastewater treatment plants [J]. Water Research, 2011,45(15):4672-4682.
[6] Wang Q, Ye L, Jiang G, et al. A free nitrous acid (FNA)-based technology for reducing sludge production [J]. Water Research, 2013,47(11):3663-3672.
[7] Anthonisen A C, Loehr R C, Prakasam T B S, et al. Inhibition of nitrification by ammonia and nitrous acid [J]. Journal Water Pollution Control Federation.1976,48(5):835-852.
[8] Ma B, Yang L, Wang Q,et al. Inactivation and adaptation of ammonia-oxidizing bacteria and nitrite-oxidizing bacteria when exposed to free nitrous acid [J]. Bioresource Technology, 2017,245(8): 1266-1270.
[9] Wang Q, Ye L, Jiang G, et al. Side-stream sludge treatment using free nitrous acid selectively eliminates nitrite oxidizing bacteria and achieves the nitrite pathway [J]. Water Research, 2014,55(10):245-55.
[10] Katsou E, Malamis S, Frison N, Fatone F. Coupling the treatment of low strength anaerobic effluent with fermented biowaste for nutrient removal via nitrite [J]. Journal of Environmental Management, 2015, 149(11):108-117.
[11] Tanyolaç D, Salih B, Tanyolaç A. Inhibition kinetics of a commercial mixed culture by ammonium sulfate [J]. Biochemical Engineering Journal, 2001,7(3):177-182.
[12] Edwards V H. The influence of high substrate concentration on microbial kinetics [J]. Biotechnology and Bioengineering, 1970,12(5): 679-712.
[13] Park S W, Bae W. Modeling kinetics of ammonium oxidation and nitrite oxidation under simultaneous inhibition by free ammonia and free nitrous acid [J]. Process Biochemistry, 2009,44(6):631-640.
[14] Hulle V, Eveline I V, Josefa L T, et al. Influence of temperature and pH on the kinetics of the Sharon nitritation process [J]. 2007,82(5):471- 480.
[15] Ganigué R, Lopez H, Balaguer M D, et al. Partial ammonium oxidation to nitrite of high ammonium content urban landfill leachates [J]. Water Research, 2007,41(15):3317–3326.
[16] Magrí A, Corominas L, López H, et al. A model for the simulation of the SHARON process: pH as a key factor [J]. Environmental Technology Letters, 2007,28(3):255-265.
[17] Andrews J F. A mathematical model for the continuous culture of microorganisms utilizing inhibitory substrates [J]. Biotechnology and Bioengineering, 1968,10(6):707-723.
[18] Haldane J B S. Enzymes [M]. Longmans Green and Co, 1930.
[19] López-Fiuza J, Buys B, Mosquera-Corral A, et al. Toxic effects exerted on methanogenic, nitrifying and denitrifying bacteria by chemicals used in a milk analysis laboratory [J]. Enzyme and Microbial Technology, 2002,31(7):976–985.
[20] Surmacz-Gorska J, Gernaey K, Demuynck C, et al. Nitrification monitoring in activated sludge by oxygen uptake rate (OUR) measurements [J]. Water Research, 1996,30(5):1228-1236.
[21] Aiba S, Shoda M, Nagatani M. Kinetics of product inhibition in alcohol fermentation [J]. Biotechnology and Bioengineering, 1968, 10(6):845-864.
[22] Tessier G. Croissance des populations bactériennes et quantité d'aliment disponible [J]. Reviews Science, 1942,80:209-216.
[23] Luong J H T. Generalization of Monod kinetics for analysis of growth data with substrate inhibition [J]. Biotechnology and Biochemistry, 1987,29(2):242-248.
[24] Han K, Levenspiel O. Extended monod kinetics for substrate, product, and cell inhibition [J]. Biotechnology and Bioengineering, 1988,32(4): 430-437.
[25] 国家环境保护局.水和废水监测分析方法 [M]. 北京:中国环境科学出版社, 1997.
[26] Husom D H, Mitra S, Ruscheweyh H J, Weber N, et al. Integrative analysis of environmental sequences using MEGAN4 [J]. Genome Research, 2011,21(9):1552-1560.
[27] Husom D H, Auch A F, Qi J, et al. MEGAN analysis of metagenomics data [J]. Genome Research, 2007,17(3):377-386.
[28] Lansing M Prescott, John P Harley, Donald A Klein.微生物学(中文版) [M]. 高等教育出版社, 493-496.
[29] 张宇坤,王淑莹,董怡君,等.游离氨和游离亚硝酸对亚硝态氮氧化菌活性的影响 [J]. 中国环境科学, 2014,34(5):1242-1247.
[30] Vadivelu V M, Yuan Z G, Fux C, et al. The inhibitory effects of free nitrous acid on the energy generation and growth processes of an enriched nitrobacter culture [J]. Environmental Science and Technology, 2006,40(14):4442-4448.
[31] Carrera J, Jubany I, Carvallo L, et al. Kinetic models for nitrification inhibition by ammonium and nitrite in a suspended and an immobilized biomass systems [J]. Process Biochemistry, 2004,39(): 1159–1165.
[32] Li Y, Li J, Wang Z, et al. Inhibition kinetics of nitritation and half-nitritation of old landfill leachate in a membrane bioreactor [J]. Journal of Bioscience and Bioengineering, 2016,123(4):482-488.
Inhibitory kinetics of free nitrous acid on.
SUN Hong-wei1,2*, YU Xue1,2, LI Wei-wei3, QI Guo-ping3, MA Juan1,2, CHENG Yong-zhi1,2, LV Xin-tao4
(1.School of Environmental and Municipal Engineering, Lanzhou Jiaotong University, Lanzhou 730070, China;2.Gansu Sewage Treatment Industry Technical Center, Lanzhou 730070, China;3.Gansu Province Light Industry Research Institute, Lanzhou 730070, China;4.Research and Development Center of Beijing Drainage Group Technology, Beijing 100022, China)., 2018,38(11):4246~4254
A sequencing batch reactor (SBR) was operated in this study to investigate the inhibitory kinetics of free nitrous acid (FNA) on. At the beginning of the experiment, FNA concentration in influent was changed to enrich. Then, the sludge of enrichmentwas employed to study the variation law of the specific nitrite oxidation rate (SNiOR) during nitrite oxidation process of batch tests. Meanwhile, metagenomic species annotation and abundance analysis showed thataccounted for 40.3% of the total bacterial population. Furthermore, kinetic model of FNA inhibition onactivity was fitted for statistical analysis. The results showed that the SNiOR increased rapidly with the increase of FNA concentration when£0.1·mg/L while decreased with the increase of FNA concentration as FNA>0.1mg/L. In particular, the SNiOR was maintained at 0gN/(gVSS·d) when FNA concentration was higher than 0.7mg/L, implying thatactivity was completely inhibited. Statistical analysis results showed that compared to Haldane, Aiba, Edwards-1#, Edwards-2# and Luong inhibition kinetics models, Han-Levenspiel model was the most suitable one for describing the inhibitory effect of FNA onactivity. The statistical constants, e.g., residual square sum (RSS) correlation coefficient (2), F value of the analysis of variance and confidence degree (P) was 0.02, 0.90, 78.1and 3.29×10-12, respectively. The dynamic constant values, e.g., maximum specific nitrite oxidation rate (max), half saturation constant (S) and critical inhibition constant (m) was 1.57gN/(gVSS·d), 0.01mg/L and 0.66mg/L, respectively.
free nitrous acid;;specific nitrite oxidation rate;inhibition kinetic;metagenome
X172,X703.5
A
1000-6923(2018)11-4246-09
孙洪伟(1976-),男,黑龙江齐齐哈尔人,教授,博士,主要从事污水生物脱氮研究.发表论文40余篇.
2018-04-11
国家自然科学基金资助项目(51668031);兰州交通大学“百名青年优秀人才培养计划”项目(152022);甘肃省重点研发计划-工业类项目(17YF1GA009)
* 责任作者, 教授, 12821306@qq.com

