基于互感差异的双拾取无线电能传输系统功率分配控制策略

陈国东, 吴剑青, 孙 跃, 陈振新, 唐春森

(1. 重庆大学自动化学院, 重庆市 400030; 2. 国网浙江省电力有限公司舟山供电公司, 浙江省舟山市 316000)

0 引言

无线电能传输(wireless power transfer,WPT)技术为电能的传输方式提供了新的思路,由于克服了传统接触式电能传输技术的因接触磨损、线路老化及接触不良等因素带来的安全风险,在工程实际中的应用日益增加[1-3]。随着近年来电力电子技术的发展和半导体器件工艺的成熟,WPT技术逐步从小功率的家居设备、医疗设备等应用拓展到中大功率的电动汽车、轨道机车等应用[4-7]。大多数的WPT系统由一个原边磁能发射端和一个副边磁能拾取端组成,通过互感耦合实现能量的无线传输,但受到拾取端器件和线圈的容量、价格等因素限制,单个拾取线圈无法满足电动巴士、轨道机车等大功率电气设备的需求。而多拾取WPT系统采用多个拾取端共同为单个大功率负载提供能量,可以克服器件容量的限制,实现大功率电能传输。

目前,多拾取WPT系统根据输出结构连接方法可以分为:独立模式、并联模式和串联模式。其中，独立模式为每个拾取对应一个负载(即多负载问题),更适用于解决多个用电设备的供电问题,相关文献研究主要集中于系统最大功率或最大效率,负载切换相关控制以及线圈位置和结构等方面。文献[8]分析了在考虑交叉耦合情况下使系统效率最高的负载计算方法,但该方法没有考虑实际负载的功率需求。文献[9]提出一种频率抖动控制方法用于解决负载接入或切出带来的系统功率变化问题。文献[10]通过调节发射端与拾取端之间的距离实时优化耦合机构的互感,从而达到功率传输的最优化,但是该方法实际操作难度大。

并联模式和串联模式主要为单一大功率用电设备解决供电问题,通过多个拾取端共同为单个负载输出能量,可以克服单个拾取端的输出电流不足或者输出电压不足问题,实现大功率电能传输。其中,并联模式可以减少变换器的电流应力[11],但在使用时必须考虑输出均流问题,相关文献研究主要集中于交叉互感对系统的影响及消除方法,输出功率均衡等方面。文献[12]通过在发射端添加补偿电容,消除拾取端线圈之间的互感,但该方法难以实现动态调节,适用于负载相对固定的系统。文献[13]从工程应用角度出发,取拾取电路中Boost电路的输入电压差作为输出电流的补偿值,实现输出均流。文献[14]考虑拾取线圈自感差异性,在相同补偿电容情况下利用交叉互感补偿拾取线圈自感差异,实现输出功率均衡。而串联模式可以减少变换器的电压应力,其变换器的输出通过串联方式相连后与负载连接,因此所有功率变换器的输出电流大小相等,不存在均流问题,但是存在拾取端功率分配问题。文献[15]针对多拾取WPT系统,基于其拾取端感应电压的差异以及负载功率需求提出了一种功率分配控制策略,一定程度上优化了系统效率。

针对双拾取WPT系统串联输出模式下的功率分配问题,本文以效率优化为目标,研究并提出一种基于各拾取端与发射端的互感差异实现拾取端功率分配的控制策略。详细分析双拾取WPT系统结构及其工作原理,结合负载实际功率需求分析耦合机构损耗的影响因素,进而提出拾取端功率分配控制策略,以降低系统在耦合机构上的功率损耗,实现功率传输容量与效率的优化控制。最后,通过实验验证该控制策略的有效性和可行性。

1 双拾取WPT系统原理分析

1.1 LCL-S型双拾取WPT系统拓扑分析

常见的4种基本补偿方式在WPT系统中得到了广泛的应用,但由于其补偿结构属于单级补偿结构,存在谐振容量小、开关器件电压和电流应力大等缺点[11]。考虑到实际系统中拾取端或负载可能移除,为了确保系统安全性和稳定性,通常在WPT系统应用中会控制原边发射线圈恒流。由于LCL-S型补偿拓扑具有发射线圈电流恒定的特点,可以减少原边控制的复杂程度,并且对于逆变电路的电流应力也比较小。因此本文考虑采用LCL-S型拓扑作为系统主电路,即原边采用LCL复合补偿方式,副边采用LC串联补偿方式。

LCL-S型双拾取WPT系统由一个原边磁能发射端(TX)和两个副边磁能拾取端(RXs)组成,基本电路结构如图1所示。原边包含一个电压型全桥逆变器和一个LCL谐振网络,每个副边包含一个整流桥和一个BUCK变换器,变换器的输出通过串联连接方式为负载RL供电。LP和LSi(i=1,2)为发射线圈和拾取线圈的自感,CP和CSi(i=1,2)为对应线圈LP和LSi(i=1,2)的补偿电容,Mi(i=1,2)为拾取线圈LSi(i=1,2)与发射线圈之间的互感。

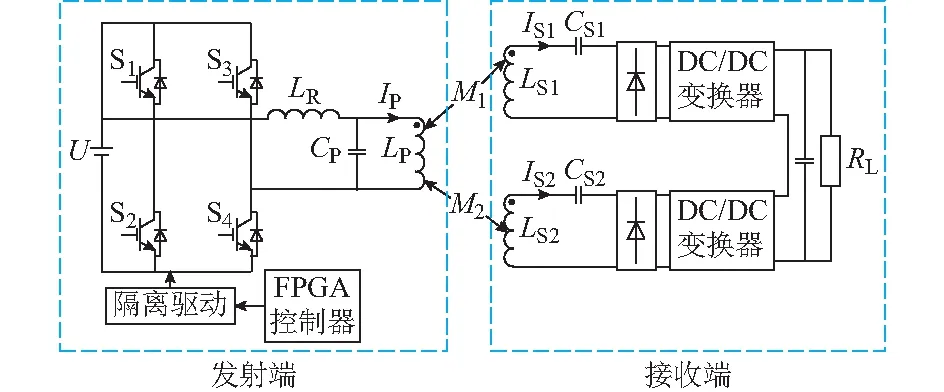
图1 LCL-S型双拾取WPT系统电路结构Fig.1 Circuit structure of LCL-S WPT system with dual-pickup coils

在实际系统设计中,为了便于系统参数设计,简化系统分析,提出以下几点假设。

1)设计原边线圈自感相同,LR=LP。

2)不计补偿线圈、发射线圈和两个拾取线圈的内阻,RR=RP=RS1=RS2=0。

3)忽略两拾取线圈之间的互感。

单个拾取端的电路结构如图2所示,其中,Ri为负载RL在第i个拾取端输出侧的等效输出阻抗,Reqi为谐振网络的等效输出阻抗,Di表示BUCK变换器的占空比。

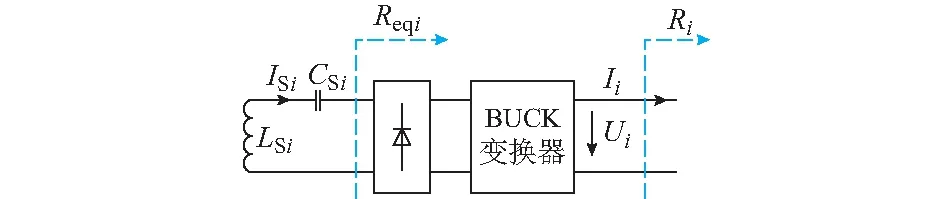
图2 单个拾取端的电路结构Fig.2 Structure of single-pickup port

考虑BUCK变换器的效率损耗,为方便分析,假设两个BUCK变换器在工作时的效率均为η,根据功率守恒定律,整流桥的输入功率等于其输出功率,当BUCK变换器工作在电流连续模式(continuous conduction mode)下,谐振网络的等效输出阻抗Reqi可近似如下[15]:

(1)

当拾取端的输出采用串联方式相接,系统运行在稳态时,各个拾取端输出侧电流相等,根据KCL和KVL可以得出拾取端BUCK变换器的端口输出特性:

(2)

1.2 LCL-S型双拾取WPT系统建模

LCL-S型双拾取WPT系统的等效电路图如图3所示。

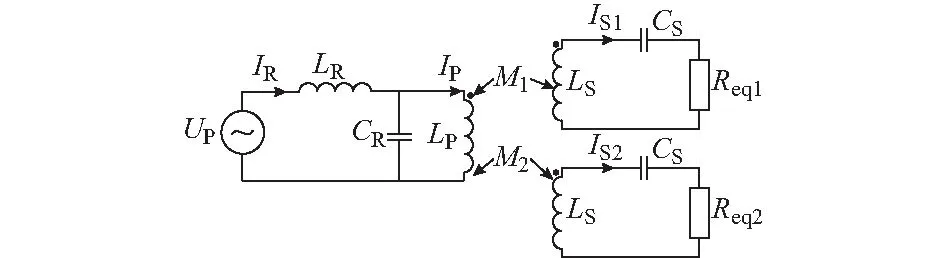
图3 LCL-S型双拾取WPT系统电路等效电路图Fig.3 Equivalent circuit of LCL-S WPT system with dual-pickup coils

图3中:IP为发射线圈电流;IR为逆变输出电流;IS1与IS2为拾取线圈电流。根据KVL可以得到双拾取WPT系统的各个电气量的相互关系表达式如下:

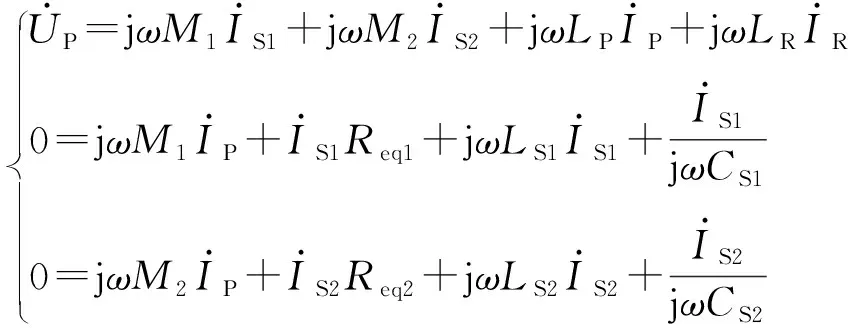
(3)

式中:ω=2πf为系统的激励电压角频率,其中,f为系统各谐振环节固有谐振频率,有

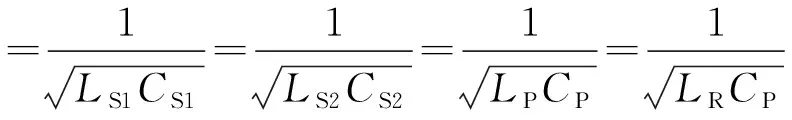
(4)

当系统工作在固有谐振频率f时,谐振电路处于谐振状态,呈纯阻性,则副边的等效输入阻抗和原边电路的输入端总阻抗可表示为:

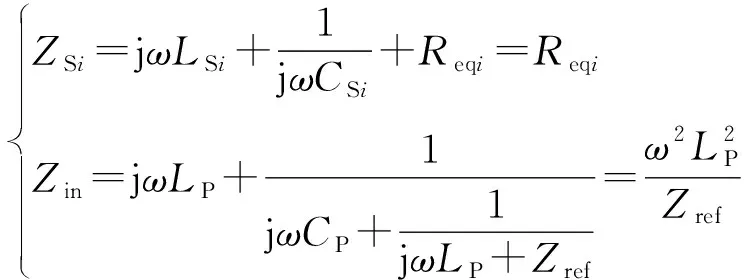
(5)

其中,Zref为副边电路反射到原边电路的反射阻抗,表示为:

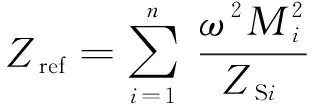
(6)

由此可以得到逆变器输出电流和原边谐振电流分别为:

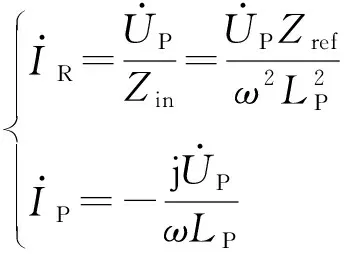
(7)

当系统工作在固有谐振频率f时,由于忽略了线圈内阻,拾取线圈上的感应电动势全部由Req1和Req2承担,再经过整流电路和BUCK电路后输出。又由于式(2)中所有变换器输出电流与负载电流相同,因此变换器输出电压可以用拾取端输出侧的等效输出阻抗与负载电流的乘积表示。结合式(3)和式(7),变换器输出电压Ui可表示为:

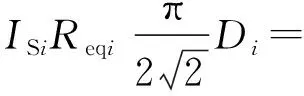
(8)

根据式(2)和式(8)可以解出在串联输出结果下拾取端输出侧的等效输出阻抗Ri为:

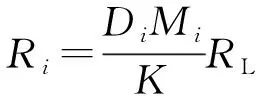
(9)

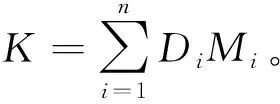
谐振网络的等效输出阻抗Reqi受到BUCK变换器占空比以及拾取线圈与发射线圈之间互感影响,根据式(1)与式(9),可以得到其与RL的关系为:

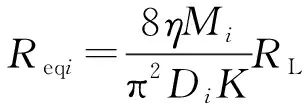
(10)

联立式(8)、式(9)和式(10),可以得到系统的拾取线圈电流和总输出电压以及总输出功率为:

(11)

2 双拾取WPT系统功率分配控制策略

从第1节的分析中可知,对于一个定参数的LCL-S型双拾取WPT系统,发射线圈电流具有恒流特性,系统的总输出功率取决于K值的设定。

将系统耦合机构上的损耗分为发射线圈功率损耗和拾取线圈功率损耗,可以表示为:

(12)

式中:A=[UPKπ2/(8LPRLη)]2RS。

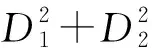
对于一个定参数的系统,在输入电压不变时,根据式(11)在系统总输出功率需求为PCMD时,参数K值唯一确定,根据柯西不等式,有

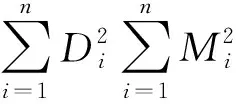
(13)

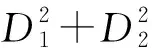
因此,在负载功率确定情况下,当BUCK变换器的占空比满足:

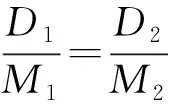
(14)

拾取线圈上的功率损耗最小,为:

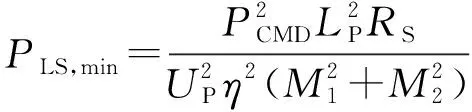
(15)

根据式(8)可得出在负载功率需求为PCMD时,各路拾取端输出电压的配置条件为:

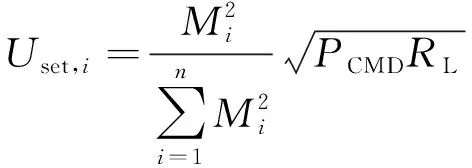
(16)

定义PCi为单个拾取端输出的功率,根据式(11)和式(16)可以得到拾取端功率容量的关系如下:

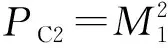
(17)

值得注意的是,式(16)和式(17)的成立必须满足以下条件:

RSi≪Reqi

(18)

当该条件不满足时,内阻RSi对电路的影响不能忽略,式(11)中将包含RSi项,从而使得式(12)无法简化。并且较大的RSi将导致较大的功率损耗,系统会因效率太低而不具实用性。因此,正常情况下,式(18)是自然满足的。

当拾取端之间存在交叉耦合时,可以利用文献[12]提出的调节电容补偿的方法来消除交叉互感对系统的影响。因此,即使拾取端之间存在互感,本文提出的控制策略也同样适用。

式(16)和式(17)的结论在Boost变换电路和Cuk变换电路中同样成立,只需将对应电压、电流和电阻公式进行替换即可得到,这里不做详细的推导。

由此可以看出,采用式(16)所给出的电压配置方法考虑了不同拾取端之间功率容量的差异,根据其功率输出能力的大小而配置其承担的负载功率。根据式(16)所设计的系统控制框图如图4所示。

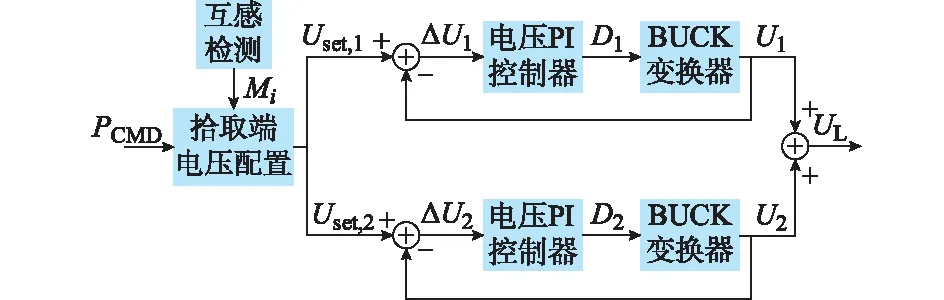
图4 LCL-S型双拾取WPT系统的控制系统框图Fig.4 Block diagram of control system of LCL-S WPT system with dual-pickup coils

图4所示控制系统通过测量拾取线圈与发射线圈之间的互感Mi,并依据负载的功率需求PCMD可以得到各个拾取输出电压的参考值Uset,i,并利用比例—积分(PI)控制器对BUCK变换器进行控制实现输出稳压,从而达到在耦合机构损耗最小情况下满足负载功率需求。对于互感在线检测目前已有相关文献研究[16],因此本控制系统不仅可以对固定式WPT系统进行系统效率优化,同样也适用于移动式WPT系统。

需要注意的是,图4所示的控制框图中Di是根据输出电压闭环负反馈由控制器确定的,在理论上满足式(14)的比例关系。但考虑到实际系统中系统电路参数的差异以及检测环节的精度,可能会导致实际工作占空比与理论占空比略有不同。

3 实验验证

为验证本文提出的建模方法以及控制策略的有效性,设计LCL-S型双拾取WPT系统的实验平台如附录A图A1所示。实验中由于线圈位置较远,

两线圈之间的互感很小,近似忽略。实验系统主要参数如下:U=100 V,f=80 kHz,LP=47.8 μH,LS1=55.04 μH,LS2=55.09 μH,M1=17.76 μH,M2=14.48 μH,RL=10 Ω,RP=0.12 Ω,RS=0.1 Ω,η=0.8。

设计系统的总负载需求功率为PCMD=40 W,根据以上负载阻值可以得到负载电压应为20 V。设置拾取端1的输出电压U1由5 V调节至15 V,而拾取端2的输出电压U2由15 V往下调节至5 V,每隔1 V对拾取线圈的电流进行记录。其中,在U1和U2均为10 V以及U1和U2分别为12 V和8 V的两种典型情况下,拾取线圈电流与输出电压的实验波形如附录A图A2所示。

附录A图A2中CH1为拾取线圈1电流,CH2为拾取线圈2电流,CH3为负载两端电压。图A2(a)为不考虑拾取端互感差异,两个拾取端均分拾取电压时,即U1=U2=10 V时的系统波形,此时负载两端电压满足20 V的设定值,由于拾取线圈2的互感小于拾取线圈1,因此在相同电压设定值情况下拾取线圈2电流更大,对应IS1=0.811 A,IS2=0.906 A。需要注意到的是,当两个拾取线圈的互感差异较大时,无视该差异均分电压将导致互感小的拾取无法达到电压设定值。图A2(b)为考虑拾取端互感差异,根据式(15)配置拾取电压,即U1=12 V,U2=8 V时的系统波形,此时负载两端电压满足20 V的设定值,此时拾取线圈1由于拥有更大的互感,因此需要承担更多的功率,对应IS1=0.952 A,IS2=0.711 A。

由于本文实验中负载为10 Ω,根据文中的系统参数可以得到副边系统的品质因数Q值约为0.74,Q值太低导致整流产生的高次谐波无法完全滤除,从而产生一定的波形畸变。从有无功率变换器、占空比大小、负载大小、滤波电容等多个方面进行分析(详见附录B),得出通过合理地设计副边系统的Q值可以有效解决拾取线圈电流畸变的问题。

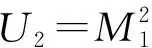
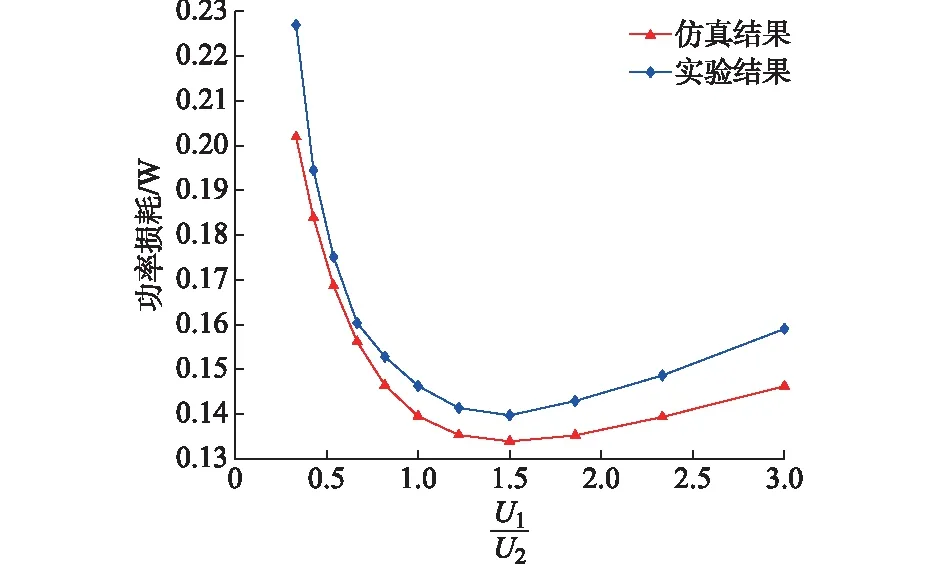
图5 实验结果和仿真结果对比Fig.5 Comparison between experimental result and simulation result

4 结语

本文通过对LCL-S型双拾取WPT系统的建模,推导了系统耦合机构的功率损耗方程,分析了耦合机构损耗最小条件,在此基础上提出一种根据系统实际互感来分配拾取端功率的控制策略,在满足负载功率需求条件下减少系统在耦合机构上的功率损耗。最后,通过仿真和实验验证了理论分析的正确性以及控制策略的有效性。

在后续研究中将考虑变换器占空比对其效率的影响,不同拾取端的变换器效率对于双拾取WPT系统效率的影响,以及对应控制系统设计方法。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。