基于隐马尔可夫模型的日内风电功率预测误差区间滚动估计

周 玮, 钟佳成, 孙 辉, 李国锋, 孔剑虹, 张富宏

(1. 大连理工大学电气工程学院, 辽宁省大连市 116024; 2. 国网大连供电公司, 辽宁省大连市 116001;3. 国网辽宁省电力有限公司, 辽宁省沈阳市 110004)

0 引言

日内优化调度对风电功率超短期预测提出了明确的要求,传统风电功率预测通常采用基于点预测的方法[1]。为量化风电功率预测结果的不确定性,可针对日内风电功率预测误差区间进行估计,使调度部门的工作人员能够提前根据风电功率预测误差的范围和预测误差的变化趋势修正各常规火电机组的发电计划,以降低由风电预测误差引起的备用需求,并降低因风电大规模并网给系统带来的风险及电力系统的运行成本。

近年来,国内外在估计风电功率预测误差方面已经有了很多研究成果,其方法主要有两类。

第一类为统计方法[2-4]。统计方法主要基于风电功率的概率分布,计算在满足一定置信水平下,风电功率误差可能落入的区间。用某种分布对风电预测误差进行近似描述,正态分布是最为普遍的假设应用;但风电功率预测误差概率分布并非完全对称的正态分布,而成偏态分布,所以可以利用参数优化后的非标准贝塔分布对功率预测误差频率分布进行拟合[2];或者根据多种分布,使用混合偏态分布模型估计短期风电预测误差分布[3]。通用分布模型的提出,用以拟合风电功率预测误差,比传统模型估计效果有所改善[4],但该模型在风机集中出力的时间段里偏差较大。统计方法需要获取风电预测误差分布特征的具体形式,但由于地域、季节的不同,该分布特征一般难以准确获取。

第二类为启发式算法。该算法主要是通过学习历史数据的规律,预测风电功率误差的上限和下限。其主要方法有神经网络法[5]、线性回归法[6]、支持向量机[7]、极限学习机[8]等方法,应用启发式算法是在历史统计数据与风电预测误差之间建立一种映射关系。该方法一般不依赖于风电功率预测误差的分布特征,同时可以以一定的概率涵盖风电预测误差的范围。

以上研究,为风电功率误差区间估计的研究提供了有益的探索。但目前大多的研究方法假定各调度时段的风电预测误差相互独立,实际中这一假设可能并不满足。当评估复杂系统异常事件(如极端气象事件)构成的不确定性时,由随机变量序列表述的事件通常是相关的[9]。马尔可夫模型能够体现相邻时段之间的相关性,本文针对风电功率预测精度随时间尺度逐步提高的特点,将隐马尔可夫模型(hidden Markov model,HMM)[10-13]引入日内风电功率预测误差处理过程,通过HMM估计一定时间段内预测误差边界及转移概率,对给定的最新日内风电功率预测值进行波动区间滚动估计。同时,基于局部加权回归散点平滑法对模型结果进行处理,增加了模型估计结果的准确度。最后,通过风电功率实际数据验证该方法的有效性。

1 HMM理论及其算法

HMM是在马尔可夫模型基础上发展起来的一种双重随机过程统计模型,具有一定状态数的隐式马尔可夫链和显式随机概率分布集合。传统的马尔可夫模型由两部分组成:马尔可夫链和状态转移矩阵。如果随机过程在已知现在状态的前提下,其未来的变化与过去的状态无关,称其具有马尔可夫性,具有马尔可夫性的随机过程被称为马尔可夫过程。而在HMM中,引入了观测概率分布,马尔可夫链的状态不再被直接观测,这时称之为隐式马尔可夫链[14]。HMM可以进行动态过程时间序列的建模,并具有强大的时序模式识别功能,适用于风、光等具有非平稳特性的预测和建模,因此,本文采用一阶HMM。一阶模型的成立本身设定了两个假设[15]: ①观测值之间严格独立,即现在的状态确定时,观测值的概率只与现在时刻有关;②状态的转移过程中下一状态只与现在状态有关,与以前所有的状态和观测值无关。

风电功率预测误差具有强波动性、强不确定性,及风电功率预测在相邻时段具有时序相关性的特点,本文将HMM引入到风电预测误差区间估计当中。利用HMM对风电功率预测误差区间进行估计,可以很好地估计出风电预测误差的范围边界,尤其是在风电预测误差在很短的时间范围内剧烈变化的时段,能更好地描述风电功率预测误差。

HMM的基本形式为λ1={S,O,A,B,π}。该模型参数如下。

1)隐式状态有限集合S

S={s1,s2,…,si,…,sM}si∈Q

(1)

式中:si为风电功率预测误差标准化数据在t时刻所处的状态,满足si∈Q;Q为随机过程可能处于的有限个高斯分布集合,Q={q1,q2,…,qi,…,qN}用来描述风电功率预测误差标准化数据的波动状态,qi表示某种高斯分布，N为状态个数,表示每个时间节点对应N个状态;M为输入样本个数。

2)可观察的序列集合O

O={o1,o2,…,ot,…,oM}

(2)

式中:ot为t时刻风电功率预测误差的标准化参数,由式(3)计算得到。

ot=zscore(λt)

(3)

(4)

式中:zscore(·)为一个整体函数,表示标准差标准化过程;λt为中间变量;ηt为对t时刻风电功率的预测值;ηreal,t为t时刻风电功率的实际出力。

3)隐式状态转移概率矩阵A

(5)

式中:Pr(·)为求取概率函数。

4)观测值概率转移矩阵B

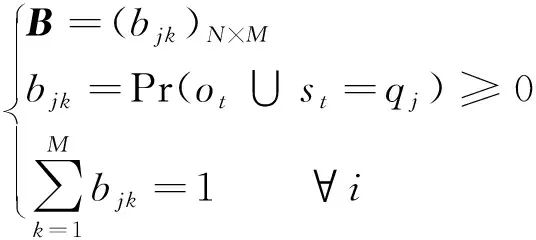
(6)

5)初始状态概率矩阵π

(7)

式中:πi为给定状态i的初始概率。

HMM根据观测值的分布分为连续型HMM(CHMM)和离散型HMM(DHMM),为得到输出状态的概率矩阵,本文采用HMM离散观测值模型。

HMM主要解决三个问题[16-17]:①评估问题,给定模型λ,计算观测序列集合O的概率,进而可对该HMM做出相关评估(前向—后向算法);②解码问题,根据已知观测序列集合O和模型λ,获取最优的隐式状态序列集合S(Viterbi算法);③学习问题,当HMM部分模型参数λ2={A,B,π}未知,对给定观测序列集合O在最大似然度下学习得到最佳模型参数(Baum-Welch 算法)。

2 基于HMM的日内风电功率波动区间估计

2.1 日内风电功率预测误差建模

对于日内风电功率预测误差,可以基于HMM建立风电功率预测误差模型来描述每个时间节点风电功率预测误差的波动过程。

风电功率预测误差的概率规律一般难以统计,只能够获得风电功率预测误差的历史数据,无法确定事件所处的状态及状态的参数。隐式状态集合S中的元素代表的是每一时刻的标准化数据属于N种高斯分布中的其中一种高斯分布,而具体属于哪一种状态及该状态对应的高斯分布的具体参数是未知的,都不能够通过观察得到,所以S称为隐式状态集合。在这个模型中,隐式状态集合S是一个马尔可夫链,状态的转移具有马尔可夫性,并且无法被观测到。考虑到风电功率预测误差的不确定性,误差观测标准化值ot被定义为服从与t时刻状态st相对应的高斯分布。

2.2 日内风电功率预测误差模型参数估计

由于风电预测误差的波动状态无法被观测得到,导致日内风电功率预测误差模型参数估计的不完整。本文采用最大期望值(expectation maximization,EM)算法来估计风电功率预测误差所处的隐式状态[18]。EM算法的实现步骤如下。

步骤E:计算对数似然函数的期望。

L(θ,θ(k))=E(lg(Pr((S,O)|θ))θ(k),O)

(8)

式中:θ为HMM中无法被观测到的参数的初始设定值,θ(k)为第k次迭代后得到的参数估计值;E(·)为求取期望的过程。

步骤M:求解使得对数似然函数最大的模型参数。

θ(k+1)=arg maxL(θ,θ(k))

(9)

式中:arg maxL(·)为当L(·)取最大值时,θ(k)的取值函数。

反复迭代直至θ(k+1)和θ(k)之间的差值达到精度要求,即为最优的模型参数。

通过EM算法可以估计得到隐式状态集合S中各元素所对应的波动状态及S中各元素所对应的高斯分布的方差σst。

2.3 日内风电功率波动区间滚动估计

不论何种预测方式,其预测结果的准确性都会呈现“近大远小”的特点,预测的周期越长、时间距离越远的结果准确性越低,误差就越大。本文采用滚动预测的方式可以适当降低由于预测周期带来的误差。

估计模型每整小时启动运行,启动时自动获取风电功率预测误差历史数据及最新的风电功率预测信息,滚动估计该风电功率预测信息中包含的未来n个时间窗口的风功率预测误差波动范围,在实际的调度过程中,每个时间窗口通常取15 min。每次启动后得到的风电功率预测误差波动范围自动覆盖上1 h后得到的结果。

将最新得到观察的序列集合O及风电功率预测序列集合Y={y1,y2,…,yn}输入到已建立的HMM中,即可得到这n个时间节点的预测误差波动状态的概率及每种状态之间的转移矩阵。

以这n个时间节点最大概率预测误差波动状态所对应的高斯分布,可计算得到n个时间节点的风电预测误差最大波动范围,同理,如果不以最大概率选择预测误差状态,则会得到不同的结果。将得到最新的风电功率预测波动区间[-ε,ε],其中ε为满足一定的置信水平α的极大误差。以n=16为例的滚动时间关系示意图见附录A图A1;HMM日内风电功率波动区间估计的流程图见附录A图A2。

3 预测误差区间评价方法

3.1 预测误差区间的处理方式

由于不同预测风电功率方法使用的历史数据、建立预测模型的不同、模型本身的误差及随机因素的影响,都存在一定误差。针对HMM对误差波动的敏感性强,区间边界存在跃动和尖峰现象,本文使用基于局部加权回归散点平滑法(LOWESS)对误差区间进行处理,LOWESS的流程图见附录A图A3。

LOWESS具有两个特点:①趋势性,经过LOWESS方法处理过的数列是个派生数列,它将沿袭原始数据的走势;②稳定性,派生出的数列修正了原始数列,相当于在一定程度上消除了受某些偶然因素影响所出现的非常波动,这样就能使派生出的数列趋势变得稳定,在数据上体现的则是稳定的延伸,某个别时间节点变化对于数列走势的影响就会变小。

3.2 区间估计评价准则

区间估计评价指标须考虑可靠性和准确性两个指标[19-20],参考文献[21]中的方法,引入预测区间覆盖率指标IPICP、预测区间平均带宽指标IPINAW、累积带宽偏差指标IAWD。

1)IPICP能够反映预测区间的准确性,该指标反映了实际值落在预测区间上下界内的概率。

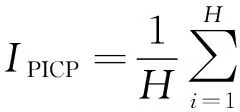
(10)

式中:H为待评价区间包含的时段数;κi为布尔量,如果实际值包含于预测区间之内,则κi=1,否则κi=0。

2)IPINAW能够反映预测区间的清晰度,避免因为单纯追求准确性,使得区间过于保守,无法提供决策价值。

(11)

式中:Ui和Li分别为预测区间的上边界和下边界;R为实际值的变化范围。

3)IAWD是一个辅助指标,能够反映出当IPICP和IPINAW一定时,实际值偏离预测区间上界(或下界)的程度。

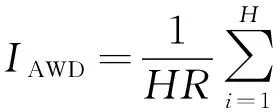
(12)

(13)

式中:ti为待评价区间内i时刻的实际值。

为保证电力系统运行的可靠性和安全性,希望IPICP的值越大越好,而IPINAW和IAWD的值越小越好。

4 算例分析

为验证所提模型的有效性,本文使用中国某省风电实际数据进行分析,该数据取样间隔为15 min,曲线如附录A图A4所示。其中蓝色曲线为风电功率预测值,红色曲线为风电功率实际出力值。预测值为每15 min得到自上报时刻起未来15 min至4 h的预测数据,时间分辨率均为15 min,经滚动获得曲线。以N=4,n=16为参数,选取不同训练样本数量,观察训练样本数量M对于模型精确度的影响,在本文中,输入样本集合即为训练样本集合。文中从数据时间节点1 001开始,以之后8 d共768个时间节点的数据作为预测样本集合,连续滚动估计测试样本数据的误差区间。

每次模型运行会得到一个从时间节点t到t+1的状态转移矩阵Ak,k表示第k次运行。若以Ak(i,j)表示矩阵A中第i行j列的元素,代表在时间节点t处于状态i,并将以Ak(i,j)的概率在时间节点t+1转移到状态j。

因本文算例部分是连续滚动估计8 d共768个时间节点的误差区间,所以这里只以第一次滚动估计得到的状态转移概率矩阵A1为例进行说明,如式(14)所示。

A1=

(14)

以上述k=1时状态转移矩阵A1为例,在本次估计中,若隐式状态在当前t时间节点处于状态1,则在下一个时间节点t+1将以0.462 963的概率转移到状态1(即保持在状态1);若隐式状态在当前t时间节点处于状态2,则在下一个时间节点t+1将以0.273 81的概率转移到状态1;若隐式状态在当前t时间节点处于状态3,则在下一个时间节点t+1将以0.043 75的概率转移到状态1;若隐式状态在当前t时间节点处于状态4,则在下一个时间节点t+1将以0的概率转移到状态1;若隐式状态在当前t时间节点处于状态1,则在下一个时间节点t+1将以0.407 407的概率转移到状态2,以此类推。

模型每次运行不仅可以估计得到当前时刻之后一段时间内风电功率预测误差区间范围,同时还可以通过状态转移概率矩阵获得该时间段内时序相关的误差状态变化趋势。决策者可以通过概率转移矩阵得到的状态变化趋势,对模型得到的结果进行修正,或者根据变化趋势对其他状态的情况作出准备。

当训练样本数目取不同数值时,IPICP,IPINAW,IAWD的变化趋势没有明显的规律性。以IPICP为例,其变化曲线如图1所示。

图1 不同输入样本数量下IPICP的比较Fig.1 Comparison results of IPICP with different numbers of input samples

附录A图A5给出了训练样本数目M取1 000,700,400,100时标准化数据的概率图,是统计学中用来描述数据正态性的。从图中可以看出,不同的训练样本,其数据的正态性有所不同,体现在图中尾部数据的偏移程度不同。偏移的数据越多,偏移的程度越大,说明整体数据中特异性的数据越多,特异性越严重,数据的正态性差。为验证训练样本的正态性是否会影响估计的准确性,在接下来的算例验证中,不固定训练样本数目,而是在每次计算之前,选取检验样本数目从100到1 000中偏度最小的样本作为训练样本。

不同偏度误差区间指标对比如表1所示。从表中可以看出选择偏度最小的样本数量,可以提升估计区间的准确度,使准确度达到90%,同时保证了较小的IPINAW,说明模型能够在保证准确性的同时不增加估计误差区间的保守性。

表1 不同偏度误差区间指标对比Table 1 Index comparison of different skewness error intervals

不同的置信水平α下IPICP和IPINAW的变化趋势如图2所示。图中表明,随着置信水平的降低,IPICP和IPINAW呈下降趋势,说明模型估计的极大误差波动区间的准确性随置信水平的下降而降低。同时,保守性也会随着置信水平降低,但这是以牺牲准确性为代价的。

图2 不同置信水平α下IPICP和IPINAW比较Fig.2 Comparison results of IPICP and IPINAW with different confidence levels

以观测样本偏度最小,风电功率预测误差波动状态数N=4,置信水平α=95%得到的效果图如图3所示。图中蓝色曲线是提前4 h风电预测误差,红色曲线是以本文方法得到的风电功率预测误差区间边界。从图中可以看出,本文方法能够很好地估计出满足置信水平的风电预测误差范围边界,尤其是在风电预测误差在很短时间范围内剧烈变化的时段,更大限度地包含风电出力的极端情况,这也是本文方法IAWD值很小的原因。

图3 风电功率误差区间估计结果Fig.3 Intervals estimation of prediction error for wind power

为验证本文方法的实用性,针对实际工程中普遍采用的按固定比例法确定误差区间和本文方法计算结果进行对比分析,如表2所示。从准确性来看,本文所提方法有将近90%的区间覆盖率,实际工程中采用的固定比例法若要达到本文方法的准确性,其IPINAW远高于本文所提方法。相同的预测区间平均带宽条件下,本文方法中IPINAW代表的准确性好。因此,固定比例法虽降低了保守性,但是是以牺牲准确性为代价的。

表2 不同方法下评价指标对比结果Table 2 Comparison of evaluation indices with different methods

通过本文方法确定的风电功率预测误差区间,对误差较为敏感,能够更好地描述由于日内风电预测不准确给系统带来的不确定性,有更强的估计准确性,不容易出现过估计,为调度人员提供足够的信息,在保障安全性的同时,使调度计划及备用安排更加经济。

5 结语

日内超短期风电功率预测误差区间估计对于含风电电力系统的运行调度有着十分重要的意义。本文提出了一种基于HMM的风电功率预测误差区间估计方法,以中国某省实际风电数据为例验证本文方法的有效性,得到如下结论。

1)HMM可以用于风电功率预测误差区间估计,该方法不仅可以提供预测误差区间范围,还能够得到与预测误差区间相关的概率转移矩阵。因此,本文方法能够丰富预测信息。

2)研究了原始样本数据对预测模型的影响,结果显示以偏度最小选取观测样本能够得到最精确的结果。

3)以本文方法和实际工程中普遍采用的按固定比例法作比较,得到的精度优于固定比例法且精度较高,具有实际应用价值。

本文模型使用的是一阶HMM进行误差区间估计。使用二阶及以上状态阶数的HMM,并通过单点滚动替换这样的手段来提高风电功率预测精度,将是后续的主要研究内容。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。