计及模型不确定性的发电机动态状态估计方法

王 义, 孙永辉, 钟永洁, 卫志农, 孙国强

(河海大学能源与电气学院, 江苏省南京市 210098)

0 引言

广域量测系统(wide-area measurement system,WAMS)的相量量测单元(phasor measurement unit,PMU)由于其量测数据的快速性和同步性,已经广泛应用于电力系统监测与控制[1-3],使机电暂态过程发电机运行状态变量可量测获取。然而,由于受到多种因素的影响,获取的原始量测数据不可避免地存在误差,直接利用该量测数据进行电力系统机电暂态分析,有可能获得错误的结果,进而导致控制系统发出错误指令,影响电力系统的安全稳定运行[4-5]。因此,有必要对机电暂态过程中发电机的运行状态进行估计,以满足实际应用需求。

近年来,基于PMU的机电暂态过程发电机动态状态估计研究引起了众多学者的广泛关注[6-17]。文献[6]依据发电机转子二阶运动方程,建立了发电机机电暂态模型,选取发电机功角和电角速度为状态量,提出了基于卡尔曼滤波的发电机状态估计方法。鉴于发电机动态方程的非线性特性,文献[7]进一步提出了基于扩展卡尔曼滤波(EKF)的动态状态估计方法。但是,由于EKF算法在基于泰勒级数展开线性化的过程中忽略高阶项,导致截断误差过大。因此,文献[8-9]提出了基于无迹卡尔曼滤波(unscented Kalman filter,UKF)的发电机状态估计方法,该方法有效提高了估计精度,取得了较好的估计效果。然而,UKF算法却存在灵活性差、参数难选取等缺点。为了克服UKF算法存在的缺点,文献[10]提出了运用容积卡尔曼滤波(cubature Kalman filter, CKF)状态估计器对发电机运行动态进行估计,其利用球面—径向规则生成Cubature点,通过发电机动态方程对Cubature点进行变换,得到发电机状态量预报值,其滤波性能和计算效率优于UKF算法。进一步,针对CKF算法在迭代过程中协方差不对称或非正定线性导致的估计精度下降问题,文献[11]提出了基于平方根CKF的发电机动态状态估计方法。另外,为了克服坏数据所导致的估计准确度下降问题,文献[12]提出鲁棒CKF发电机动态估计器,能够有效抑制量测坏数据对动态状态估计的影响。文献[13-14]提出了运用粒子滤波器(particle filter,PF)动态估计发电机状态,PF以贝叶斯估计理论为基础,能够较精确地估计非高斯非线性系统的状态。但是,PF在计算重要性密度函数时未考虑最新的量测信息,所以当预测先验与似然函数重叠较少时,可能偏离真实的后验分布[15-16]。针对该问题,文献[17]进一步提出了基于无迹粒子滤波算法的发电机动态状态估计方法。

然而,需要指出的是,上述这些方法大多是建立在发电机模型精确获取基础上的,并未计及模型不确定性对发电机动态估计的影响。而在工程实际应用中发电机模型参数往往是无法或很难准确获取的,如系统噪声所满足的统计规律,不同运行状态下发电机机械功率参数等。模型不确定性会导致状态估计准确度的下降甚至失效[18-19],进而影响系统的准确监测与安全运行。

针对模型不确定性所引起的发电机状态估计精度降低甚至发散问题,本文提出了一种基于自适应H∞扩展卡尔曼滤波(AHEKF)的发电机动态状态估计方法。仿真结果表明,所提方法对模型不确定性具有较高的鲁棒性,估计性能优于EKF算法和H∞扩展卡尔曼滤波(HEKF) 算法,有良好的估计效果。

1 动态状态估计基本理论

电力系统动态状态估计依据系统量测信息和拓扑结构信息,对系统的运行状态变量进行动态感知。动态状态估计不仅可以减小或消除量测误差,获取当前时间断面的状态量,而且可以预测下一时刻的状态值。

不失一般性,发电机动态状态估计状态方程和量测方程的可表示为:

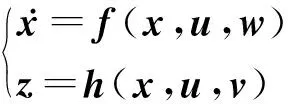
(1)

式中:x为系统状态变量;u为控制变量;z为量测变量;f(·)表示发电机的状态方程;h(·)表示发电机量测方程;w和v分别为系统噪声和量测噪声,一般假设其是均值为0,w和v相互独立;误差方差矩阵分别为Q和R的正态分布。

为了动态估计计算分析,连续模型须进一步离散化,采用欧拉公式为:

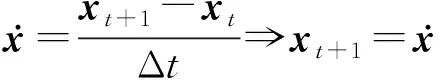
(2)

式中:下标t和t+1表示对应变量的时刻值;Δt为离散步长。

运用式(2)把式(1)的连续微分形式方程处理得到其对应的离散形式为:

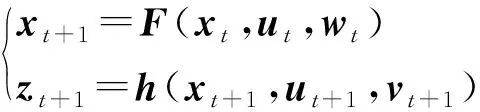
(3)

式中:F(·)表示状态方程f(·)的差分方程形式。

2 发电机动态状态估计模型

2.1 状态方程和量测方程

由文献[10,14]可知,发电机动态状态估计模型由两部分构成,即系统方程和量测方程,构建准确的系统方程对于保证滤波算法的精度至关重要。由于在事故过程中,电力系统网络拓扑结构发生改变,系统状态也会发生突变,所以,无法进行传统的状态估计[14]。但是,发电机在此动态过程中始终满足转子运动方程。因此,在发电机动态状态估计研究时常选取不会突变的发电机转子功角和电角速度作为状态估计变量[6,17]。

同步发电机的经典二阶模型,数学模型简洁,便于大规模电力系统的分析计算,其转子满足的运动微分方程表示为[6,14,17]:

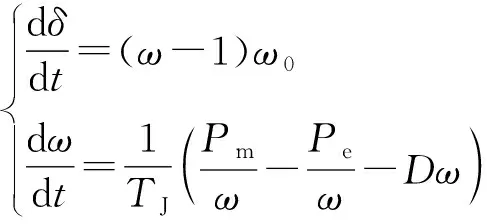
(4)

式中:δ为发电机转子功角;ω和ω0分别为发电机转子角速度和同步转速;Pm为发电机机械功率的标幺值;Pe为发电机电磁功率的标幺值;TJ和D分别为发电机惯性时间常数和阻尼系数。

选定发电机的状态估计变量为x=ω〗T,假设发电机的电磁功率和机械功率已知(具体仿真测试时,发电机的电磁功率需要量测获取,而发电机的机械功率则默认为常数,其值为发生故障前的稳定运行值),则此时发电机运动方程与外部网络解耦,则式(4)对应状态方程形式可整理为:

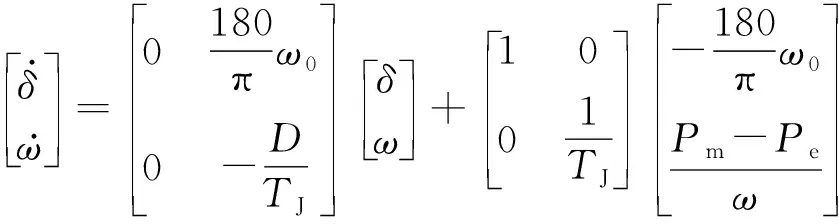
(5)

进一步和式(1)中的状态方程对照,可以确定发电机动态状态估计模型的状态变量和控制变量,根据式(2),得出离散的发电机动态状态方程。

对于量测方程而言,由于PMU技术发展和使用,发电机的功角和电角速度这两个状态变量均可通过PMU量测获取,因此,量测方程可设置为:

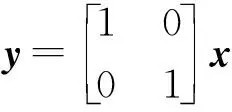
(6)

式中:y为量测变量。

2.2 误差分析

在建立发电机动态状态估计模型后,为了运用滤波方法进行动态估计,需要进一步计算获取系统量测噪声和系统噪声方差阵。本文采用噪声方差阵设置方法与文献[17]相同,具体设置方法此处不再赘述,直接给定设两个方差矩阵设置情况,其中系统噪声满足的协方差矩阵为:

(7)

量测噪声所满足的协方差矩阵为:

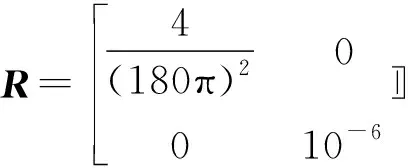
(8)

3 AHEKF法动态状态估计

3.1 约束准则

对于实际电力系统而言,模型的不确定性主要包含两个方面：其一是噪声所满足的统计特性很难准确获取；其二是系统模型的一些参数和输入值未知或者不精确。这些不确定性将会对状态估计结果产生巨大影响,使得估计结果精度严重降低甚至发散。

为了保证所设计的滤波器估计误差有有限上界,同时最小化该约束上界,提升滤波器对模型不确定性的鲁棒性,滤波器须满足以下约束准则[18-19],即

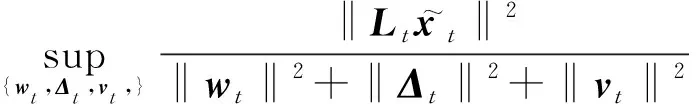
(9)

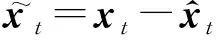
3.2 AHEKF算法

为了提升状态估计器的鲁棒性,改善系统模型不确定性下状态估计效果,本文提出了基于AHEKF的动态状态估计方法。该方法基于式(9) 建立的约束准则,利用鲁棒H∞理论最小化模型不确定性所引起的误差上界[20];并借助自适应技术,实时在线调整预测误差协方差矩阵,解决了约束上界γ难获取的问题。另外,利用文献[21]中的噪声协方差矩阵自适应估计技术,实时动态估计系统噪声协方差矩阵,减小了未知系统噪声对动态估计的影响。运用AHEKF算法对发电机动态状态估计具体步骤如下。

3.2.1步骤1:预测步

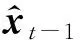
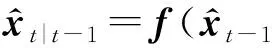
(10)

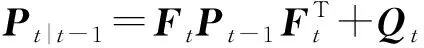
(11)

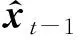
3.2.2步骤2:误差协方差自适应更新

采用自适应技术计算并更新t时刻预测误差协方差矩阵Ψt|t-1,计算公式为:

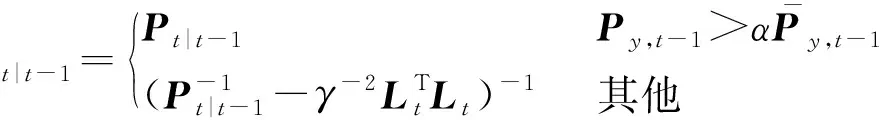
(12)

式中:α为一个待设定的正常数,用于调节动态过程中误差协方差自适应变换的阈值。

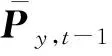
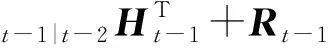
(13)

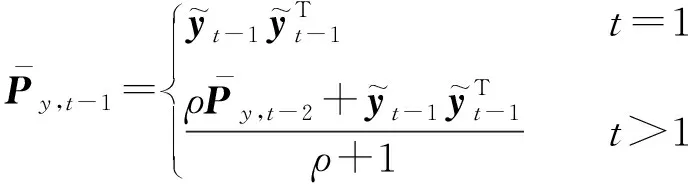
(14)

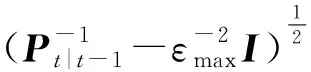
(15)

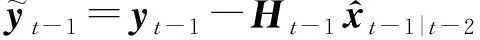
3.2.3步骤3:滤波步

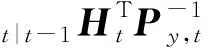
(16)

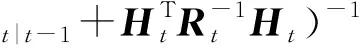
(17)

(18)

3.2.4步骤4:系统噪声协方差阵自适应更新

1)计算新息序列,计算公式为:

(19)

式中:st为t时刻的信息序列。

2)取移动窗口大小为L时,计算窗口内新息序列st的平均值,即信息矩阵Cvt,其计算公式为:

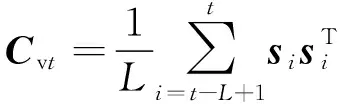
(20)

3)在上一步的基础上,动态计算t+1时刻系统噪声协方差矩阵Qt+1计算公式为:

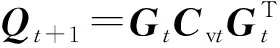
(21)

式中:Gt为t时刻滤波增益值。

AHEKF算法避免了HEKF算法中不确定约束上界γ和系统噪声统计特性难获取的问题,对外界变化能力适应更强,具有更高的滤波精度和鲁棒性。

3.3 本文算法实施流程图

通过上节分析可知,发电机状态方程为非线性系统,所以可以利用本文提出的AHEKF算法对发电机动态过程中的状态变量进行追踪估计,算法的具体实施流程如图1所示。

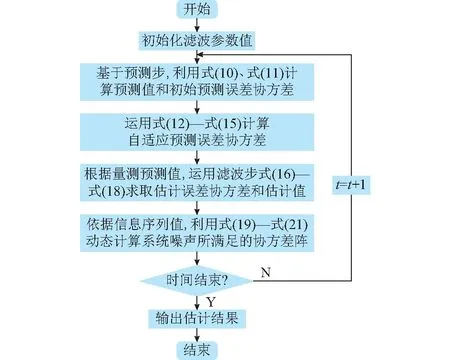
图1 AHEKF算法流程图Fig.1 Flow chart of AHEKF algorithm

4 仿真算例分析

4.1 量化评估系数

为了量化评估AHEKF算法的有效性,同时对比分析与HEKF和EKF算法之间的滤波性能,定义滤波系数η以及指标μ为:

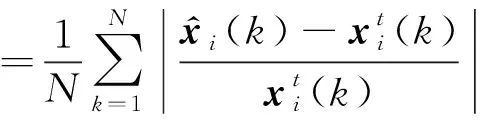
(22)

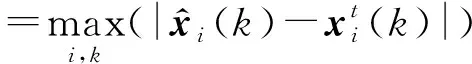
(23)

4.2 基本测试

为验证所提算法的有效性,选用WSCC 3机9节点系统作为基本测试系统,系统结构图如附录A图A1所示。选取发电机G1,G2作为研究对象,仿真测试时,将调速器的作用考虑在内,其中发电机采用经典模型[20]。三台发电机的惯性时间常数TJ取值分别为47.28,12.8,6.02;阻尼系数D取值为2,并假定在第50周期时,节点7-8支路首端发生三相金属性短路故障,第56周期时短路故障消失。

运用BPA软件模拟PMU数据采集,获取发电机运行真实值。量测数据值由真实值叠加随机噪声形成。本发明在进行仿真实验时取前300周期(1周期为0.02 s)量测值进行算法验证,即N为300。分别运用EKF,HEKF和AHEKF算法对发电机G1和G2的状态变量进行估计,估计时状态变量的初值取上一时刻静态值,其中AHEKF滤波参数分别设置为α=0.01,εmax=20,系统噪声动态估计窗口值L取为50,初始协方差矩阵P0取对应维度的单位矩阵,系统噪声和量测噪声所满足的协方差矩阵分别采用式(7)和式(8)中给定的值,EKF和HEKF算法相关参数取值与AHEKF算法相同。在WSCC 3机9节点系统中,不同方法对发电机G1的状态估计结果对比如图2所示。

从图中可以看出,在故障出现前,三种算法的跟踪效果和滤波精度基本一致,当故障出现后,EKF算法虽然能跟踪状态变化,但精度很低;HEKF算法由于计及了模型线性化截断误差的影响,相比EKF算法精度有所提高,但精度低于AHEKF算法。而本文所提出的AHEKF算法通过自适应技术在线调整预测误差协方差阵,且同时计及了模型的截断误差,所以和上述两种方法相比,AHEKF算法在跟踪速度和精度上均有所提高。基于上述分析,可以看出AHEKF算法在稳态发生负荷突变时能够有效地滤除噪声,保持较高的滤波精度,且AHEKF算法每次迭代耗时小于20 ms,可以满足实时在线跟踪估计的条件(PMU采样周期为20 ms时),发电机G2的状态估计结果对比图见附录A图A2,遗忘因子ρ取值对算法计算精度的影响和模型不确定情形下发电机G1状态估计结果见附录B。

为了更为直观地比较不同算法的状态估计结果,本文采用式(22)和式(23)定义的平均相对误差η和最大绝对误差μ滤波系数进行方法性能之间的对比分析,不同方法动态状态估计指标对比如表1所示。

表1 发电机G1和G2的不同算法动态状态估计指标Table 1 Dynamic state estimation indices of different algorithms for generator G1 and G2

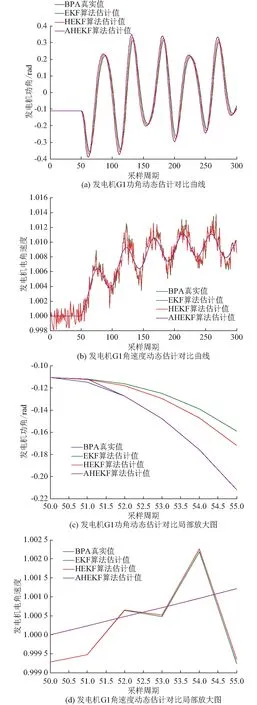
图2 发电机G1状态量状态估计结果对比Fig.2 Comparison of state estimation results of G1

从表1可以看出,和EKF和HEKF算法相比,AHEKF算法在平均相对误差和最大绝对误差滤波性能指标上均明显优于EKF和HEKF算法,即AHEKF算法的滤波精度更高,滤波效果更好。

4.3 不确定性测试

在实际电力系统分析中,系统模型的某些参数和输入值可能是未知的或者不精确的,不仅如此,系统量测噪声所满足的统计特性也很难精确获取。这些模型的不确定性,无疑将会严重影响滤波算法的状态估计性能,降低估计精度甚至无法收敛。

为了验证本文所提方法针对此种情形的有效性,对某实际大区域电网系统进行仿真测试,选取其中一台发电机出线回路设置三相短路故障,设该发电机编号为G4,故障发生于第40周期,在第43周期对故障清除。在进行发电机状态变量估计时,设发电机机械功率参数无法准确获取,不确定范围设置为10%～25%,同时设定发电机量测噪声协方差矩阵无法准确获取,取其为真实值的50倍,协方差矩阵的初始值P0取对应维度的单位矩阵,状态变量的初值x0取为上一时刻的静态状态估计值。

分别运用EKF,HEKF和AHEKF算法,对发电机G4的状态变量进行动态估计,状态估计结果如图3所示。

从图3(a)和(b)可以看出,EKF算法此时虽然能大致跟踪发电机状态变量的动态变化趋势,但是由于模型参数和噪声的不确定性,此时EKF算法的精度和跟踪速度已无法满足需求。而HEKF算法由于计及了模型不确定性的影响,所以其跟踪速度和精度相比于EKF算法而言有所改善,但估计误差依然较大。进一步,从局部放大图3(c)和(d)可以看出,AHEKF算法能够快速准确跟踪发电机状态变量的动态变化,这是因为AHEKF算法不但计及了模型不确定性,且自适应计算预测误差协方差和系统噪声协方差阵,提高对模型不确定性的鲁棒性和估计精度。

不同算法的动态状态估计指标对比如表2所示。从表2可以看出,AHEKF算法在平均相对误差和最大绝对误差指标上滤波效果明显优于EKF和HEKF算法,针对模型的不确定性具有很好的鲁棒性。

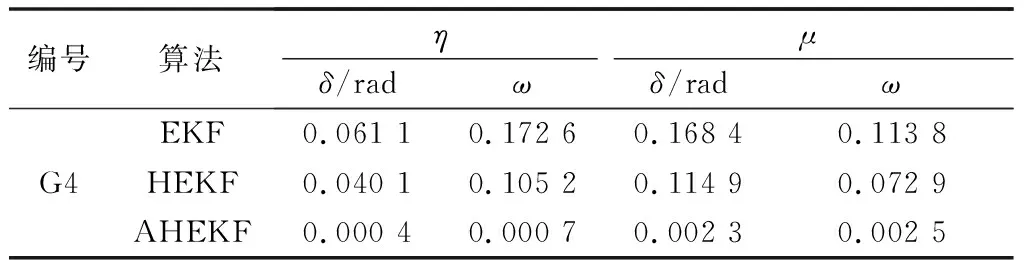
表2 发电机G4的不同算法动态状态估计指标Table 2 Dynamic state estimation indices of different algorithms for generator G4

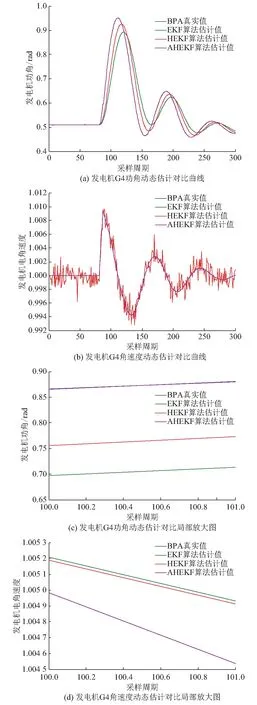
图3 发电机G4状态量状态估计结果对比Fig.3 Comparison of state estimation results of G4

5 结语

本文针对实际电力系统中模型不确定性问题,提出了一种基于AHEKF的发电机动态状态估计方法。避免了HEKF算法约束上界难以选取的问题,且提高了滤波精度。该方法对模型不确定性的鲁棒性更强,较于EKF和HEKF算法具有更高的精度,能够更好地满足实际应用。后续研究将重点关注噪声存在奇异值情况下的发电机动态状态估计问题,此外还将讨论量测信号传递过程中数据丢包缺失等特殊动态状态估计问题。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。