基于聚类分析的课堂教学质量评价研究

董晓萌，程珍珍

(渭南师范学院 数理学院，陕西 渭南 714099)

我国早在西周就建立了教育考评制度,那时学校对教育、教学进行考核、评价的内容和标准是世界上最早的教学评价。隋炀帝大业二年,开始实行科举制,但是试题量少,知识面窄,没有客观评分标准,需要改进。近代教育评价的发展是从改进主观性考试开始的。[1]19世纪末，欧美教育与心理学借助心理学、统计学和实验等科学方法,改革传统考试。20世纪初,美国心理学家桑代克于1904年发表《心理与社会测量》，介绍了心理统计方法和编制测量的基本原理。仅仅通过测验进行教育评价具有局限性,因而推动了教育评价的出现。[2]290-2921993年，数据挖掘技术首次被应用到教学评价中,在教育评价方面取得了重大突破。2000年，史晓燕提出双向评价主体、综合性评价方式、多个方向评价角度的评价模式。[3]从2005年开始数据挖掘的教育应用已成为很多国际会议研究的主题,而且还创办了教育挖掘杂志(JEMD)。[4]目前,国内外教育越来越重视数据挖掘技术以及各种统计算法在教育中的应用,同时也越来越关注教育评价的具体实施。本文针对聚类分析算法在课堂教学质量评价中的应用进行研究。

一、聚类分析

(一)聚类分析的定义

聚类分析是研究对样品(或变量)进行分类的一种多元统计分析方法。聚类的基本思想是:先把n个样本(或变量)各自看作一类，选择相似程度最大的样本作为一类，再选择相似程度次大再归类，依次类推，继续操作。[5]216-259聚类分析根据客观需要可分为两种:样品聚类和指标聚类。按其聚类的方法可分为以下几种:系统聚类法、调优法(动态聚类法)、最优分割法(有序样品聚类法)、模糊聚类法、图论聚类法、聚类预报法。[6]111-138

为了对样本(或变量)进行聚类，就要研究它们之间的关系，常用计算公式如下:

(1)明氏距离

dij(q)=[∑mt=1|xit-xjt|q]1q。

当q=1时的一阶明氏距离为绝对值距离:

dij(1)=∑mt=1|xit-xjt|。

当q=2时的二阶明氏距离为欧氏距离:

dij(2)=∑mt=1|xit-xjt|2。

当q趋于时为切比雪夫距离:

dij()=max1≤t≤m|xit-xjt|。

(2)兰氏距离(要求xij≥0)

dij(L)=1m∑mt=1|xit-xjt|(xit+xjt)。

(3)马氏距离

dij2(M)=(X(i)-X(j))′S-1(X(i)-X(j))。

其中：S-1为样本协方差阵的逆矩阵。

(二)K均值聚类算法

1.K均值聚类算法描述

K均值聚类算法属于非系统聚类法，是一种快速聚类法,通过不停地迭代，聚类域中全部的样本到聚类中心距离的平方和误差最小。[7]

其代价函数如下:

J(c(1),c(2),…,c(m),μ1,…,μk)

2.K均值聚类算法原理

(1)将所有样品分成K个初始类。[8](2)通过欧氏距离将每个样品划入离中心最近的类中,并对得到与失去样品的类重新计算重心坐标。(3)重复第二个步骤，直到全部样品都不能再分配为止。[9]

二、聚类分析在学生学习效果评价中的应用

(一)学习效果评价样本选取

选取某高校数理专业100名学生的期末成绩作为研究样本，利用统计分析软件SPSS 21.0对学生成绩进行聚类分析[10]64-67。

(二)聚类分析过程

进入SPSS软件,打开相关数据文档,依次选择“分析”“分类”“K平均值聚类”命令,把100名学生的成绩分为3个聚类数[12],最终聚类结果如表1所示。

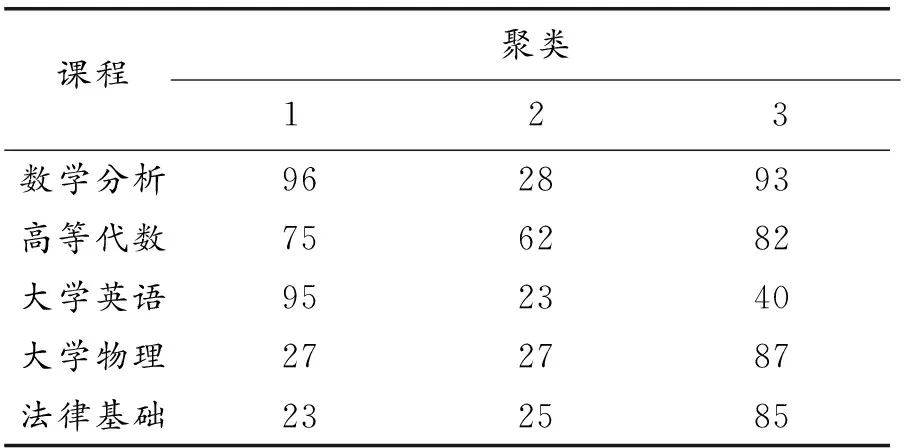
表1 初始聚类中心

表2 最终聚类中心

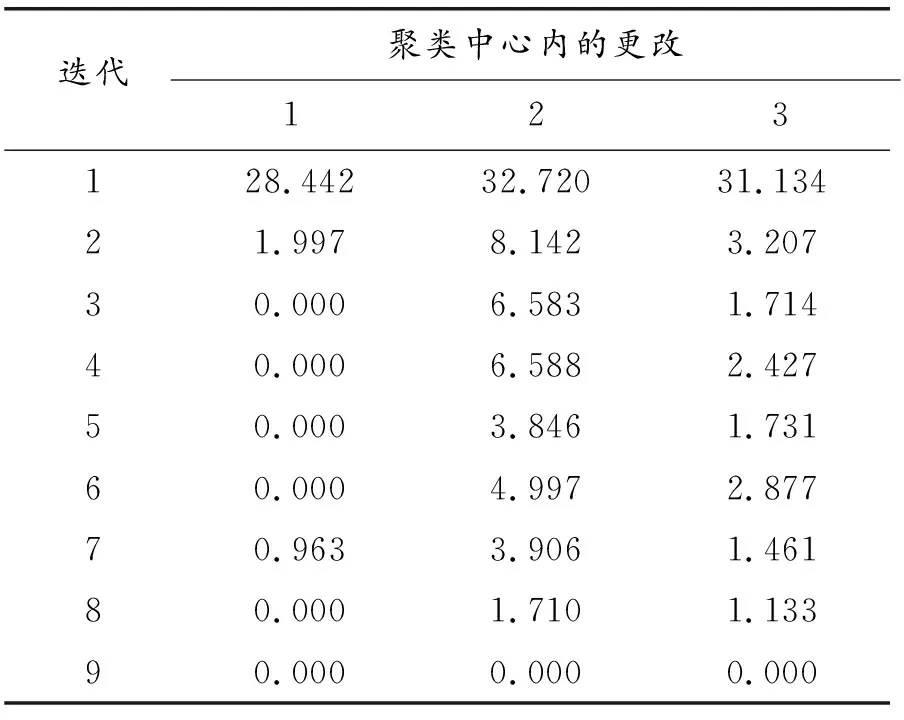
表3 迭代历史记录

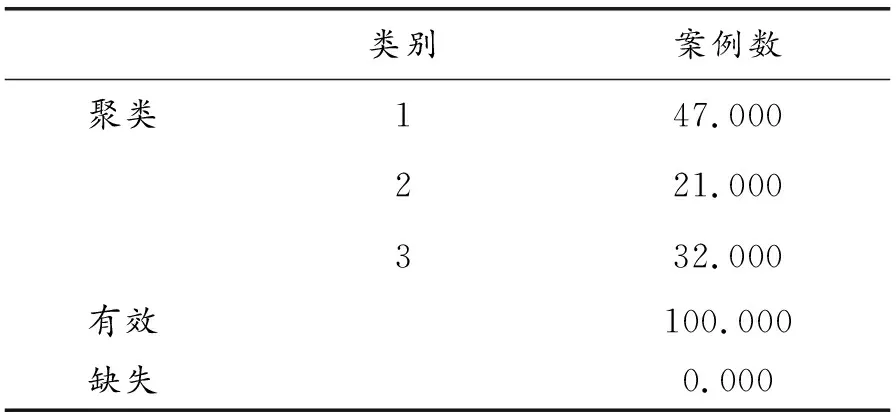
表4 每个聚类中的案例数

根据表2可知,第3类为成绩较好的学生,第1类为成绩中等学生,第2类为成绩较差学生。表3迭代历史记录中，由于聚类中心内没有改动或改动较小而达到收敛。任何中心的最大绝对坐标更改为0.000，当前迭代为9,初始中心间的最小距离为99.905。由表4可知成绩较好的学生占32%,成绩中等的学生占47%,成绩较差的学生占21%。案例处理摘要如表5所示。根据表6可知,在5门课中,法律基础与数学分析差距较大,法律基础和大学物理教师应该多注意课堂中学生的反应能力,适时调整授课方式,从而激发学生的学习兴趣,注重课堂学习效率,以提高学生学习成绩。

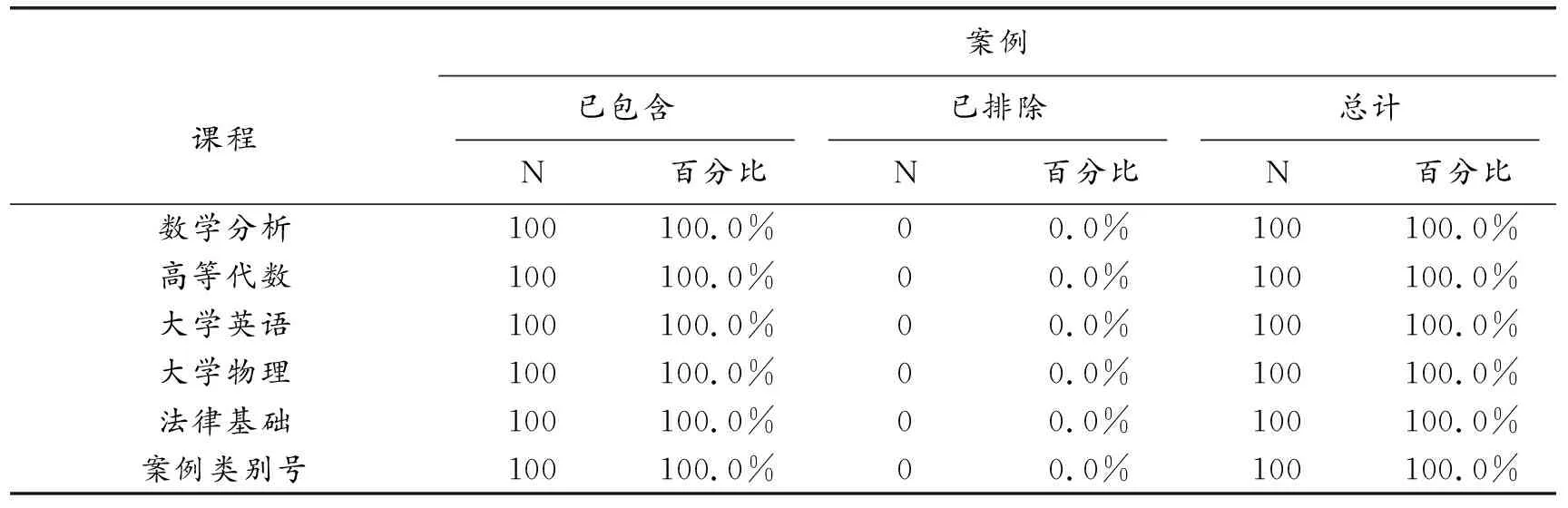
表5 案例处理摘要

表6 最终结果分析报告

三、聚类分析在教学效果评价中的应用

(一)建立指标体系

表7 课堂教学质量评价指标

在对教师进行评价的信息中,整理100张各个学科的评价表,作为研究数据。参考了相关文献[7]的教学质量评价指标,设计出了如表7所示的课堂教学质量评价指标体系。

该评价指标体系表每个二级指标5分,总分为100分,这个指标体系是通过整理每个学科评价指标的共同特征得出的,适用于各个学科。评价标准如表8所示。

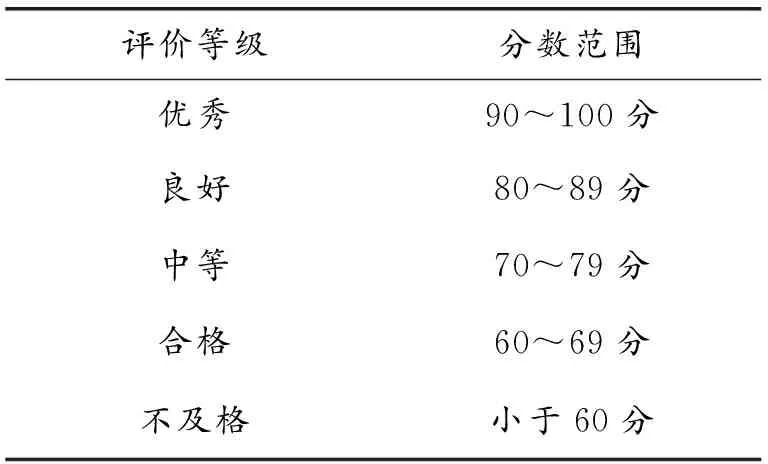
表8 评价等级标准对应表

该指标体系具有如下特点:(1)结构清晰,一目了然,易于对教师教学效果及时评价。(2)考虑要素较为齐全,将教师在课堂中所实施的每一个环节罗列得较详细,利用此评价体系对所有教师进行评价,公正合理,也有利于学校领导对教师素质进行宏观把握。[11]

(二)聚类分析过程

整理可得如表9所示的数据样本。

(三)结果分析

运用K-Means聚类算法对这些数据进行研究,将数据分为3个等级,经过聚类分析后的结果如表10所示。

从表10可以看出:

第一个等级总共有35个样本,所占比例35%;

第二个等级总共有43个样本,所占比例43%;

第三个等级总共有22个样本,所占比例22%。

对于学生成绩的分类如表11所示。

表9 教学评价数据样本

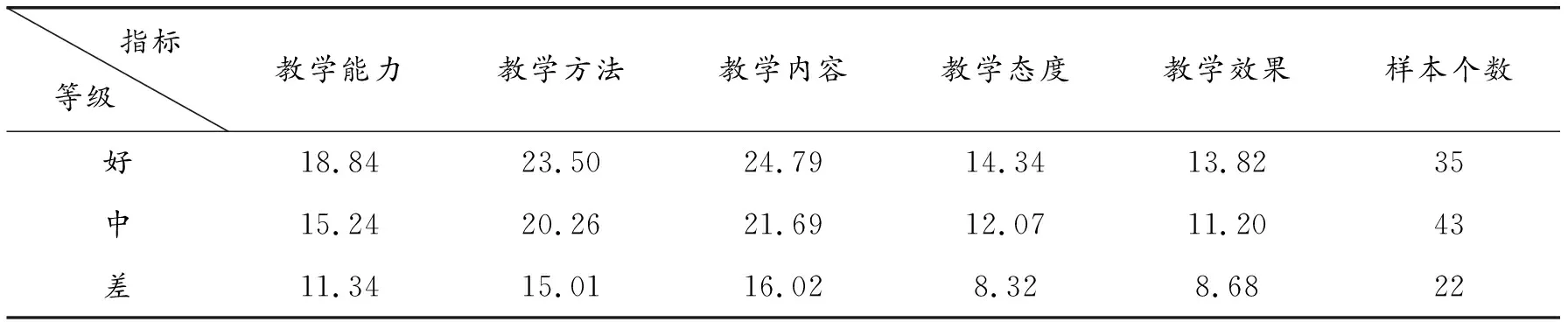
表10 聚类结果

表11 学生成绩分布情况

通过实验数据分析得出,学生成绩分布情况的3个等级(32%、48%、20%)和教师评价的3个等级所占的比例(35%、43%、22%)基本相同,增加权重后,5个项目的分数如下:

教学能力= 18.84×32%+15.24×48%+

11.34×20%=15.612,

15.612/20=78.06%;

教学方法=23.3×32%+20.26×48%+

15.01×20%=20.1828,

20.1828/25≈80.73%;

教学内容=24.79×32%+21.69×48%+

16.02×20%=21.548,

21.548/25≈86.19%;

教学态度=14.34×32%+12.065×48%+

8.32×20%=12.044,

12.044/15≈80.29%;

教学效果=13.82×32%+11.20×48%+

8.68×20%=11.5344,

11.5344/15≈76.90%。

从上算过程可以看出各项指标最终得分从高到低依次是教学内容(21.548)、教学方法(20.1828)、教学能力(15.612)、教学态度(12.044)、教学效果(11.5344)。总体来说,教学情况中等偏上,但是教学效果和教学态度所占比重相对较低,再次对照前文设计的教学质量评价指标,得出结论。在教师态度方面,教师应该端正教学态度,认真备课,高效运用课堂时间,学生也需要积极参与到课堂教学活动中,实现课堂教学目标,按时完成作业,学校也应注重教学效果的提高,提升学生各个方面的能力与个人素质。