排列熵优化改进变模态分解算法诊断齿轮箱故障

王志坚，常 雪，王俊元※，杜文华，段能全，党长营



排列熵优化改进变模态分解算法诊断齿轮箱故障

王志坚1，常 雪2，王俊元1※，杜文华1，段能全1，党长营1

（1. 中北大学机械工程学院，太原 030051；2. 重庆大学机械工程学院，重庆 400044）

为了准确提取齿轮箱中复合故障特征，该文选用变模态分解（variational mode decomposition，VMD）对振动信号进行处理，它能够将信号分解为多个固有模态函数（intrinsic mode function，IMF），但需预设分解层数和惩罚因子；因此，为了能够自适应地确定分解层数，该文提出了排列熵优化算法(permutation entroy optimization，PEO)，该算法可以根据待分解信号的特点自适应的确定分解层数；同时，为了解决VMD算法对噪声的敏感性，该文根据噪声辅助数据分析的思想，提出了改进VMD算法（modified variable modal decomposition，MVMD），该算法首先添加成对符号相反的高斯白噪声到原始信号，再利用VMD算法对其进行分解，经过多次循环，原始信号中的噪声相互抵消，而后将每次循环得到的每层IMF分别进行集成平均。利用该算法分别对含有多故障特征的齿轮箱仿真信号及实测信号进行处理，均提取出了故障特征。该文所提方法对封闭式功率流试验台进行复合故障提取，160和360 Hz的故障频率分别被提取出。该方法为齿轮箱复合故障诊断提供新思路。

齿轮；算法；噪声；多故障；排列熵；变模态分解

0 引 言

滚动轴承和齿轮等在农用机械如变速箱等旋转机构中起着重要作用，与其他零件相比，发生故障的概率较高，不可预测性较强[1]。由于齿轮箱内部结构较为复杂，当发生故障时，其故障类型多为复合故障，且其故障特征常常被淹没在强背景噪声中，因此，需要开发一种有效的自适应故障提取方法[2-3]。

经过国内外诸多科研工作者的不断探索，复合故障特征提取的方法也层出不穷。现阶段，非参数型降噪方法如经验模态分解和局部均值分解、参数型降噪方法如总体经验模态分解，已经被运用于复合故障诊断当中，但都会由于噪声干扰导致模态混叠现象[4-6]。

2014年，Dragomiretskiy等提出了一种新的信号处理算法，即变分模态分解[7](variational mode decomposition，VMD)。VMD具有坚实的理论基础，分解精度较高[8]。但该算法需要预先设定分解层数，而值往往只能凭经验而定，因此，分解结果很容易受到人为因素的影响而出现过分解或者欠分解现象，即当取值过大时，会产生过分解现象，分解出异常的白噪声分量；而当取值过小时则会出现欠分解现象，导致部分故障特征未被提取出来。除此之外，VMD算法对噪声比较敏感[9-11]，即分解结果容易受到背景噪声的影响，特别是在强背景噪声环境下，更容易产生由噪声引起的虚假分量，而对于后续的故障识别，虚假分量的产生容易导致误诊断[12-15]。

对于分解层数的自适应确定方法，Yi等[16]利用粒子群优化算法（particle swarm optimization，PSO）确定了VMD算法中的分解层数；Zhang等[17]利用蝗虫优化算法（grasshopper optimization algorithm，GOA）对VMD算法中的参数进行了优化。除此之外，还有学者利用蚁群算法[18]、人工鱼群算法[19]等其他优化算法对VMD算法中的参数进行优化。相比于凭经验确定值，这些优化算法能够根据原始信号自动确定值，具有很好的自适应性。但这些优化算法的弊端也十分明显，都存在计算量大、冗余度高、计算效率低等问题[20]。

基于此本文提出一种基于排列熵的优化算法。从噪声辅助数据分析[21]的角度改进VMD，进一步提高信号的信噪比。同时为了减小重构误差，使所添加的白噪声被完全中和，每次循环时，添加2个幅值相等、符号相反的白噪声到原始信号，然后再利用VMD算法分别对其进行分解，最终经过多次循环，使原始信号中的噪声相互抵消；将每次循环得到的各层IMF（intrinsic mode function）分别进行集成平均，再根据集成均值的结果对信号进行重构[22]；对重构信号再次进行VMD分解，作为MVMD算法最终的结果输出。

1 排列熵和变分模态分解基本理论

1.1 排列熵算法的原理

排列熵（permutation entroy，PE）是由Bandt等[23]提出的一种可以检测时间序列随机性和动力学突变的方法，该算法具有原理简单、计算效率高、鲁棒性好等优点，适用于非线性数据分析[24]，该算法的具体步骤如下

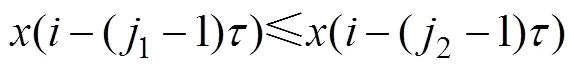
式中P表示第个符号出现的概率；H表示时间序列的复杂和随机程度，H越大，说明时间序列越随机，H越小，说明时间序列越规则。

1.2 变分模态分解

VMD算法中的每一个IMF分量的中心频率以及带宽在迭代求解过程中不断更新，最终的分解结果将根据原始信号频域特性进行自适应分解，得到个IMFs，而模型的约束条件是这个IMFs之和等于输入的原信号。约束变分模型的具体构造步骤如下

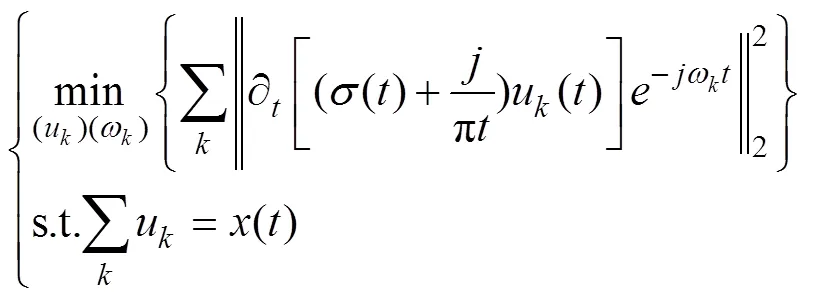
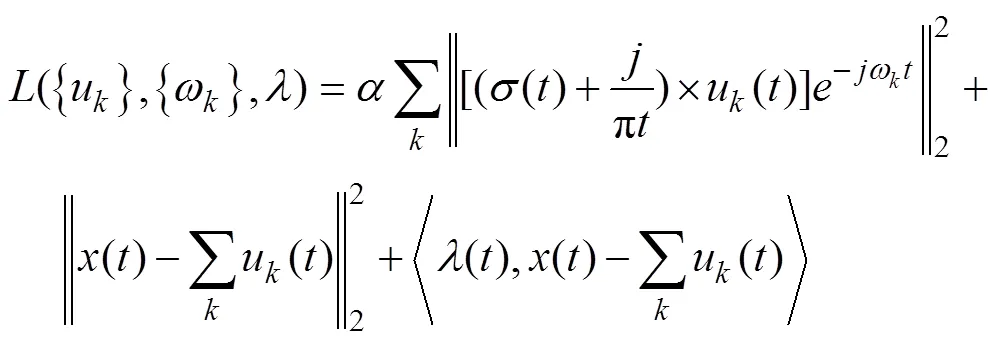
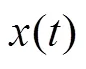
2 VMD算法改进

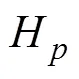
该算法的具体步骤如下

1）设定的初始值为2，排列熵的阈值取经验值0.6；

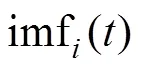
为了提高信噪比，本文提出一种基于VMD的降噪方法，即改进的VMD算法（modified VMD，MVMD）。根据文献[26]可知，CEEMD为了能够减小重构误差，使所添加的白噪声被完全中和，所以在向待分解信号中添加白噪声时，所添加的白噪声为正负白噪声对，通过该文献中的仿真与试验分析可知，相比于EEMD中单纯的添加正白噪声，CEEMD中添加正负白噪声对的方法达到了降低重构误差、促进白噪声相互中和的目的。因此，基于正负白噪声对在降低重构误差方面的显著效果，本文所提出的MVMD在添加辅助白噪声时，也采取添加正负白噪声对的思想，即每次循环时所添加的白噪声为2个幅值相等、符号相反的正负白噪声对，加上正负白噪声之间的中和作用，在实现降噪目的的同时又不引入新的噪声。加入辅助白噪声后，将得到2个待分解信号，然后再利用VMD算法分别对其进行分解，经过多次循环，原始信号中的噪声将相互抵消，最终将每次循环得到的各层IMF分别进行集成平均，根据集成均值的结果对信号进行重构，对重构信号再次进行VMD分解的具体步骤如下

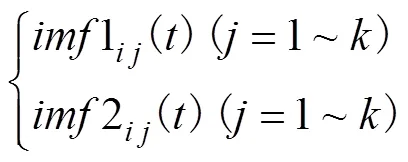
4）重复步骤2)、3)，且每次循环开始时加入新的高斯白噪声对；

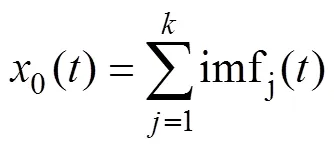
PEO-MVMD的流程如图1所示。

注：k为分解层数；N为循环次数。下同。

3 仿真信号分析

齿轮箱发生复合故障时，其振动信号往往是多调制源共存的。因此，采用齿轮故障仿真信号和滚动轴承故障仿真信号进行分析，构造如下

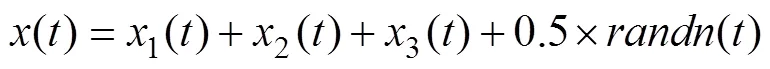
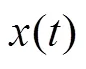
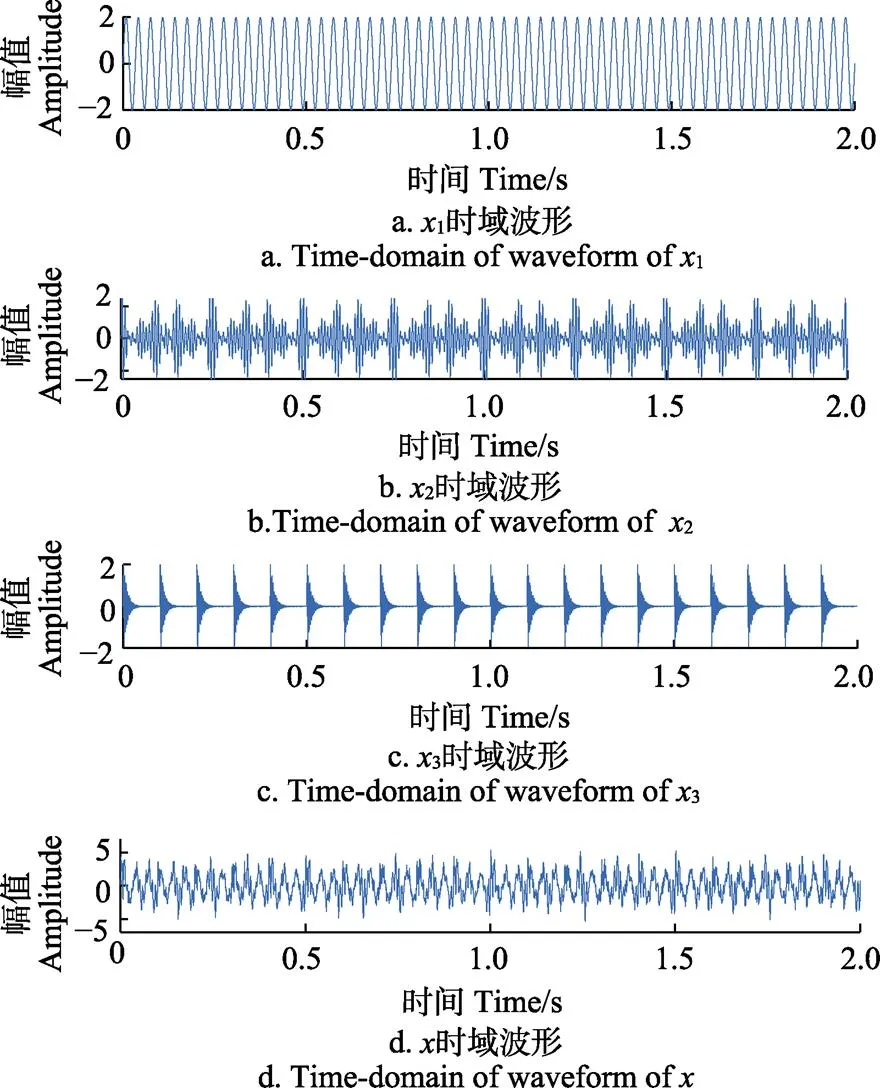
图2 仿真信号的时域波形

注：IMF为固有模态函数，下同。

MVMD算法中需要设置循环次数和所添加的白噪声幅值std。兼顾信号处理的效率，本文取循环次数=100；当白噪声幅值std取0.15时，重构信号的信噪比最高，即降噪效果最好，因此，对于仿真信号，取MVMD算法中所添加白噪声幅值为0.15。

VMD分解结果如图5所示，原始信号中30 Hz的低频成分被成功的提取出来；但中频的120 Hz信号，由于受到强背景噪声的干扰，被分解到了IMF2和IMF3这2个模态中，发生了模态混叠现象，且频谱特征十分微弱，易造成误诊断。MVMD分解结果如图6所示，在IMF1中，原始信号中30 Hz的低频信号的频谱特征十分明显；在IMF2中，调幅信号的120 Hz中心频率以及2个调制频率也都成功的从含有噪声的原始信号中分离出来，且边频带均匀对称的分布在主频两侧；在IMF3中，280 Hz的中心频率以及均匀分布在其两侧的10 Hz多条边频带也十分突出，虽然在500 Hz附近出现了残余噪声，但相比于280 Hz的主要频率成分，噪声成分十分微弱，对故障特征的识别影响不大。对MVMD分解后的信号与原仿真信号进行重构，结果如图7所示，尽管第3层有少量的残余噪声存在，但是重构效果很好。

图4 EEMD分解后的IMFs与其对应的频谱

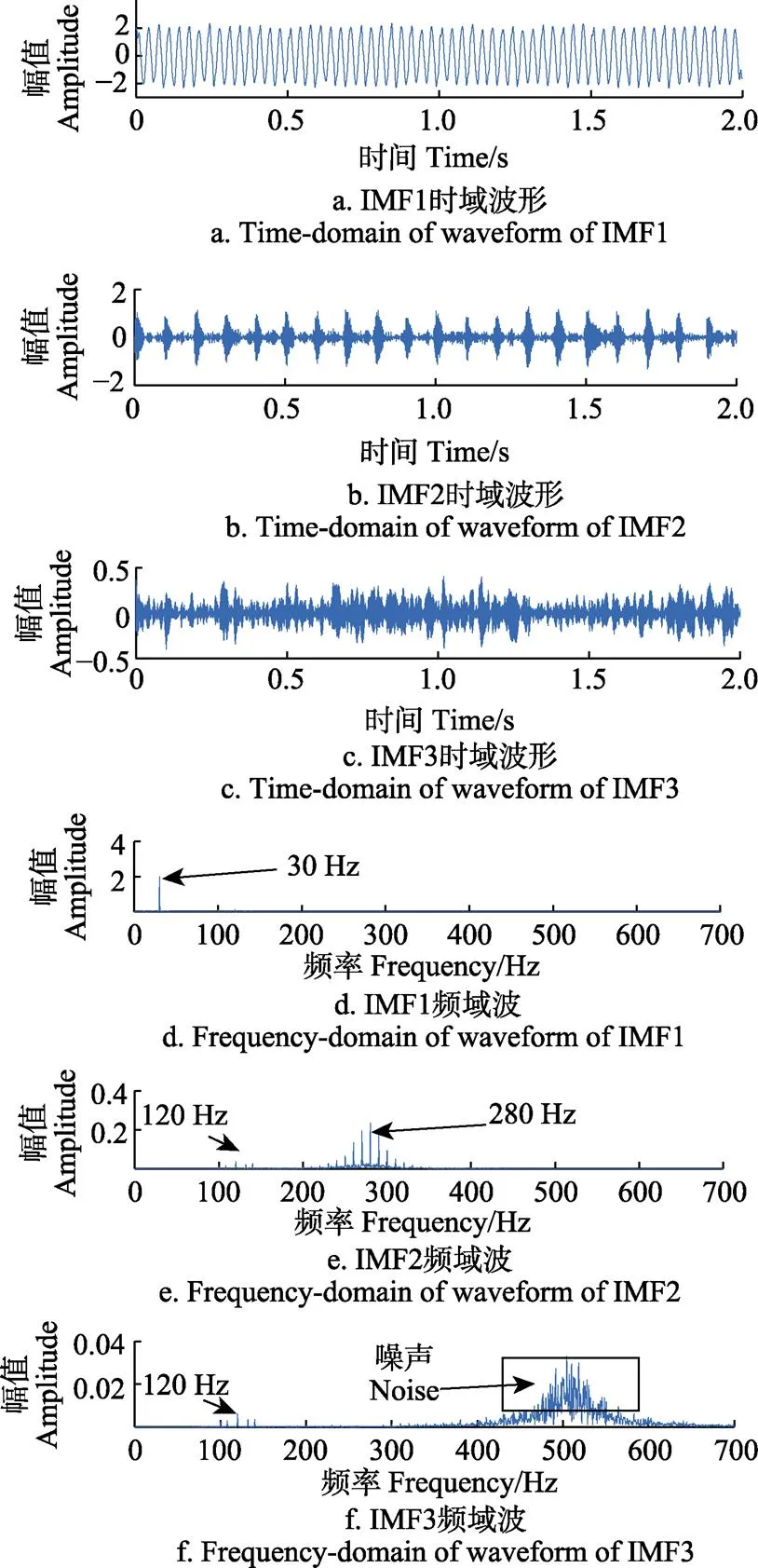
图5 VMD分解后的IMFs与其对应的频谱 Fig.5 IMFs and spectrum after VMD

图6 MVMD分解后的IMFs与其对应的频谱 Fig.6 IMFs and spectrum after MVVM

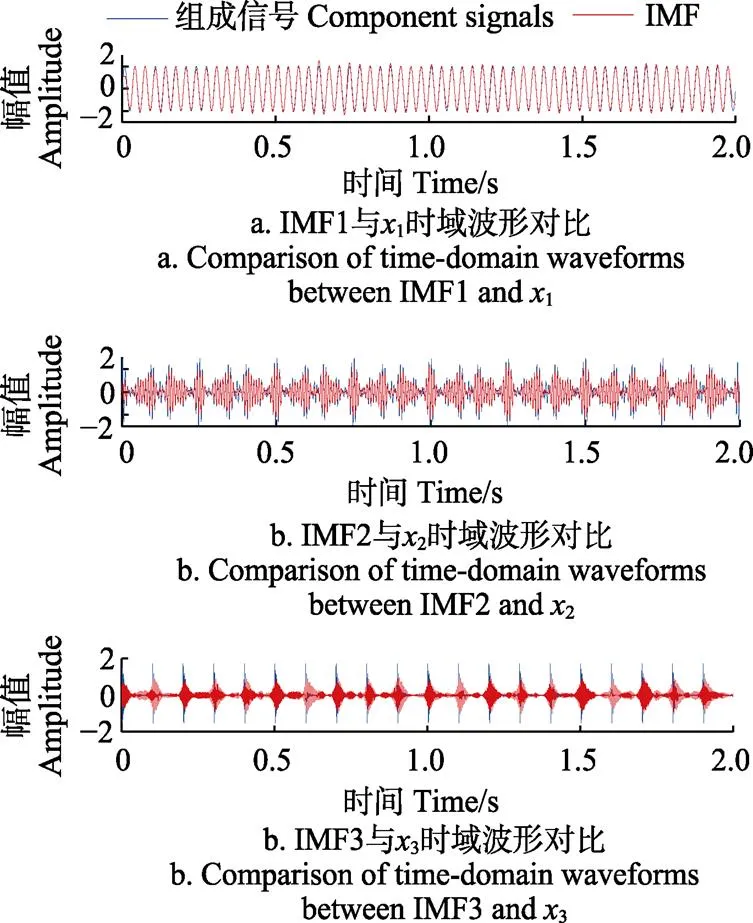
图7 MVMD分解得到的IMF与组成信号对比

4 验证试验

4.1 试验方法与设置

1. 调速电机2. 联轴器3. 陪试齿轮箱4. 转速扭转仪5. 扭力杆 6. 试验齿轮箱7. 三向加速度传感器1 8. 三向加速度传感器2

1. Speed regulating motor 2. Clutch 3. Companion gearbox 4. Rotating speed torsion meter 5. Torsion bar 6. Test gear box 7. Triaxial acceleration sensor 1 8. Triaxial acceleration sensor 2

图8 齿轮传动试验台

Fig.8 Gear transmission test bench

如图9所示，本试验中齿轮箱的复合故障包括齿轮剥落和轴承外圈故障。其中齿轮剥落通过齿轮疲劳试验产生，外圈故障通过电火花加工方法人为植入。外圈故障160.2 Hz、齿轮啮合频率360 Hz。

a. 齿轮剥落 a. Spalling failure of gearb.电火花加工外圈裂缝 b.Electric spark machining bearing outer ring crack

4.2 VMD分解结果

为验证本文所提算法的有效性，分别采用VMD和基于PEO-MVMD对上述复合故障信号进行分解。图10为VMD的分解结果，有混叠现象，第二层含有160 Hz的特征信息，此外第二层中齿轮的啮合频率360 Hz峰值较小。

图10 VMD分解后的IMFs与其对应的频谱

4.3 MVMD分解结果

采用PEO算法确定分解层数，设定初始值为2，根据是否出现过分解进行循环迭代，查找的最优值。最终PEO算法输出的的最优值为2；此外，取白噪声幅值std为0.85，循环次数=100。MVMD算法对上述齿轮箱复合故障信号进行分解。结果如图11所示，齿轮箱中外圈故障频率160 Hz以及齿轮故障特征频率360 Hz及其2倍频720 Hz均被成功提取出来，而且频率幅值远大于VMD提取结果，相对于VMD效果更佳。再次验证了文中所提方法的有效性。

图11 MVMD分解后的IMFs与其对应的频谱

5 结 论

本文提出了基于变模态分解的改进算法，即首先采用PEO算法根据待分解信号的特点自适应地确定所需要分解的层数，再利用降噪效果优异的MVMD对原始信号进行分解。通过对齿轮箱试验信号进行分析，试验结果表明，相比于VMD，本文提出的基于PEO的MVMD具有自适应性和强降噪性能，诊断出了封闭式功率流试验台中的轴承外圈故障频率和齿轮啮合频率，分别为160和360 Hz，能够自适应确定VMD的值，PEO算法输出的分解层数最优值为2，并成功提取出齿轮故障特征的2倍频720 Hz。

[1] Liang X, Zuo M J, Feng Z. Dynamic modeling of gearbox faults: A review[J]. Mechanical Systems & Signal Processing, 2018, 98: 852－876.

[2] 王志坚，韩振南，刘邱祖，等. 基于MED-EEMD的滚动轴承微弱故障特征提取[J]. 农业工程学报，2014，30(23)：70－78. Wang Zhijian, Han Zhennan, Liu Qiuzu, et al. Feature extraction of rolling bearing's weak fault based on MED-EEMD[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2014, 30(23): 70－78. (in Chinese with English abstract)

[3] Wang Z, Wang J, Zhao Z, et al. A novel method for multi-fault feature extraction of a gearbox under strong background noise[J]. Entropy, 2017, 20(1): 10－26.

[4] 周士帅，窦东阳，薛斌. 基于LMD和MED的滚动轴承故障特征提取方法[J]. 农业工程学报，2016，32(23)：70－76. Zhou Shishuai, Dou Dongyang, Xue Bin. Fault feature extraction method for rolling element bearings based on LMD and MED[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(23): 70－76. (in Chinese with English abstract)

[5] Tang G, Luo G, Zhang W, et al. Underdetermined blind source separation with variational mode decomposition for compound roller bearing fault signals[J]. Sensors, 2016, 16(6): 897－914.

[6] He S, Chen J, Zhou Z, et al. Multifractal entropy based adaptive multiwavelet construction and its application for mechanical compound-fault diagnosis[J]. Mechanical Systems & Signal Processing, 2016, 76: 742－758.

[7] Dragomiretskiy K, Zosso D. Variational mode decomposition[J]. IEEE Transactions on Signal Processing, 2014, 62(3): 531－544.

[8] 王新，闫文源. 基于变分模态分解和SVM的滚动轴承故障诊断[J]. 振动与冲击，2017，36(18)：252－256. Wang Xin, Yan Wenyuan. Fault diagnosis of roller bearings based on the variational mode decomposition and SVM[J]. Journal of Vibration & Shock, 2017, 36(18): 252－256. (in Chinese with English abstract)

[9] Zhao X, Zhang S, Zhishen L I, et al. Application of new denoising method based on VMD in fault feature extraction[J]. Journal of Vibration Measurement & Diagnosis, 2018, 38(1): 1－12.

[10] Xu A, Yan J, Wu X, et al. Rotating machinery fault feature extraction based on VMD and MP algorithm[J]. Foreign Electronic Measurement Technology. DOI:10.16450/j.cnki. issn.1004-6801.2018.02

[11] Mohanty S, Gupta K K, Raju K S. Hurst based vibro-acoustic feature extraction of bearing using EMD and VMD[J]. Measurement, 2018, 117: 200－220.

[12] Chen L, Xiao C, Li X, et al. A seismic fault recognition method based on ant colony optimization[J]. Journal of Applied Geophysics, 2018, 152: 1－8.

[13] Wang Z, Jia L, Qin Y. Adaptive diagnosis for rotating machineries using information geometrical kernel-ELM based on VMD-SVD[J]. Entropy, 2018, 20(1): 73－91.

[14] Wang ZJ, Wang J Y. A novel method for multi-fault feature extraction of a gear box under Strong background noise[J]. Entropy, 2017, 20(1): 10.

[15] Li Z, Chen J, Zi Y, et al. Independence-oriented VMD to identify fault feature for wheel set bearing fault diagnosis of high speed locomotive[J]. Mechanical Systems & Signal Processing, 2017, 85: 512－529.

[16] Yi C, Lv Y, Dang Z. A fault diagnosis scheme for rolling bearing based on particle swarm optimization in variational mode decomposition[J]. Shock and Vibration, 2016:9372691. http://dx.doi.org/10.1155/2016/9372691.

[17] Zhang X, Miao Q, Zhang H, et al. A parameter adaptive VMD method based on grasshopper optimization algorithm to analyze vibration signals from rotating machinery[J]. Mechanical Systems & Signal Processing, 2018, 108: 58－72.

[18] Zhou Y, Fazhi H E, Qiu Y. Dynamic strategy based parallel ant colony optimization on GPUs for TSPs[J]. Science China (Information Sciences), 2017, 60(6): 260－262.

[19] Shen W, Guo X, Wu C, et al. Forecasting stock indices using radial basis function neural networks optimized by artificial fish swarm algorithm[J]. Knowledge-Based Systems, 2011, 24(3): 378－385.

[20] Huang N, Chen H, Cai G, et al. Mechanical fault diagnosis of high voltage circuit breakers based on variational mode decomposition and multi-layer classifier[J]. Sensors, 2016, 16(11): 1887. DOI: 10.3390/s16111887

[21] Lee D H, Ahn J H, Koh B H. Fault detection of bearing systems through EEMD and optimization algorithm[J]. Sensors, 2017, 17(11): 2477. DOI:10.3390/s17112477

[22] Singh J, Darpe A K, Singh S P. Bearing damage assessment using Jensen-Rényi Divergence based on EEMD[J]. Mechanical Systems & Signal Processing, 2017, 87: 307－339.

[23] Bandt C, Pompe B. Permutation entropy: A natural complexity measure for time series[J]. Physical Review Letters, 2002, 88(17): 174102. DOI:10.1103/PhysRevLett. 8.174102

[24] Frank T D. Delay fokker-planck equations, perturbation theory, and data analysis for nonlinear stochastic systems with time delays[J]. Physical Review E Statistical Nonlinear & Soft Matter Physics, 2005, 71(3): 1－14.

[25] 郑近德，程军圣，杨宇. 改进的EEMD算法及其应用研究[J]. 振动与冲击，2013，32(21)：21－26.

[26] Yeh J R, Shieh J S, Huang N E. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method[J]. Advances in Adaptive Data Analysis, 2011, 2(2): 135－156.

Gearbox fault diagnosis based on permutation entropy optimized variational mode decomposition

Wang Zhijian1, Chang Xue2, Wang Junyuan1※, Du Wenhua1, Duan Nengquan1, Dang Changying1

(1.030051,; 2.400044,)

gearbox composite fault diagnosis has received extensive attention. The composite fault is that 2 or more faults occur simultaneously in the mechanical equipment. Due to the different degrees of damage of the composite fault, the complicated transmission path of the fault characteristic signal, and the interference of the background noise, the strength between the fault components is not balance. The weak fault features are usually overwhelmed by strong faults or noise and the strong faults are weakened by the high-frequency energy in the process of transmission, it is easy to be missed or misdiagnosis, especially in the case of variable speed and variable load, the coupling of composite fault features poses great challenge to the healthy and reasonable diagnosis of mechanical equipment. With the development of computer technology, some new novel adaptive noise reduction methods are proposed, including parametric decomposition methods and nonparametric decomposition methods, but they are more or less affected by noise interference and modal aliasing. Variational mode decomposition(VMD) decompose a complex signal into several different time scales, and each time scale contains a center frequency, which can overcome the modal aliasing phenomenon, variational mode decomposition is widely applied to gearbox composite fault diagnosis, and has achieved amazing results, but it needs to preset the decomposition layersand penalty factor, and is sensitive to the background noise. In order to adaptively determine the number of decomposition layers, this paper proposed permutation entropy optimization algorithm, which can adaptively determine the number of decomposition layersaccording to the characteristics of the signal to be decomposed. In order to solve the sensitivity of VMD to noise, this paper proposed modified variational mode decomposition(MVMD) based on the idea of noise aided data analysis. The algorithm first added the opposite gauss white noise to the original signal, and then used VMD to decompose it. After repeated cycles, the noise in the original signal would offset each other, then the ensemble average is generated for each IMF（intrinsic mode function） in each cycle, and the signal was reconstructed according to the result of ensemble mean. The VMD decomposition of the reconstructed signal was taken as the final output result of MVMD. This algorithm was used to process the gear box simulation signal and the measured signal with multiple fault features respectively, and the decomposition results showed that the algorithm can not only improve the signal to noise ratio(SNR) of the signal effectively, but also successfully extract the multiple fault features of the gear box in the strong noise environment, the fault frequencies of 160 and 360 Hz were extracted respectively which correspond to the bearing outer ring frequency and the gear meshing frequency. This method provides a new idea for gearbox composite fault diagnosis, it can not only overcome the interference of strong noise, but also accurately extract fault characteristics. In the future work, the research group will introduces the intelligent algorithm into the variational mode decomposition to determine the number of layers decomposed adaptively, at the same time, the combination of variational mode decomposition and support vector machine or neural network can improve the efficiency of intelligent fault diagnosis, this is a new idea for the healthy operation of agricultural machinery.

gears; algorithm; noises; multi-fault; permutation entropy; variable modal decomposition

王志坚，常 雪，王俊元，杜文华，段能全，党长营. 排列熵优化改进变模态分解算法诊断齿轮箱故障[J]. 农业工程学报，2018，34(23)：59－66. doi：10.11975/j.issn.1002-6819.2018.23.007 http://www.tcsae.org

Wang Zhijian, Chang Xue, Wang Junyuan, Du Wenhua, Duan Nengquan, Dang Changying. Gearbox fault diagnosis based on permutation entropy optimized variational mode decomposition[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(23): 59－66. (in Chinese with English abstract) doi：10.11975/j.issn.1002-6819.2018.23.007 http://www.tcsae.org

2018-05-26

2018-9-30

国家自然科学基金（59975064）

王志坚，博士，副教授，主要研究方向为旋转机械复合故障诊断。Email：wangzhijian1013@163.com

10.11975/j.issn.1002-6819.2018.23.007

TN911.72；TP206

A

1002-6819(2018)-23-0059-08