研究抛体运动的分解方法

武银根

研究平抛运动时，通常把平抛运动分解成水平方向的匀速直线运动和竖直方向的自由落体运动，即使教师讲解新课时，也是通过各种实验来说明这种分解的意义，其实，把曲线运动分解成两个直线运动是没有规定的，取任意两个方向都可以按照平行四边形定则进行分解，因此研究平抛运动也就不一定沿水平和竖直两个方向分解，二是根据需要取两个方向进行分解，有时候方向取得好会使问题变得非常简单.

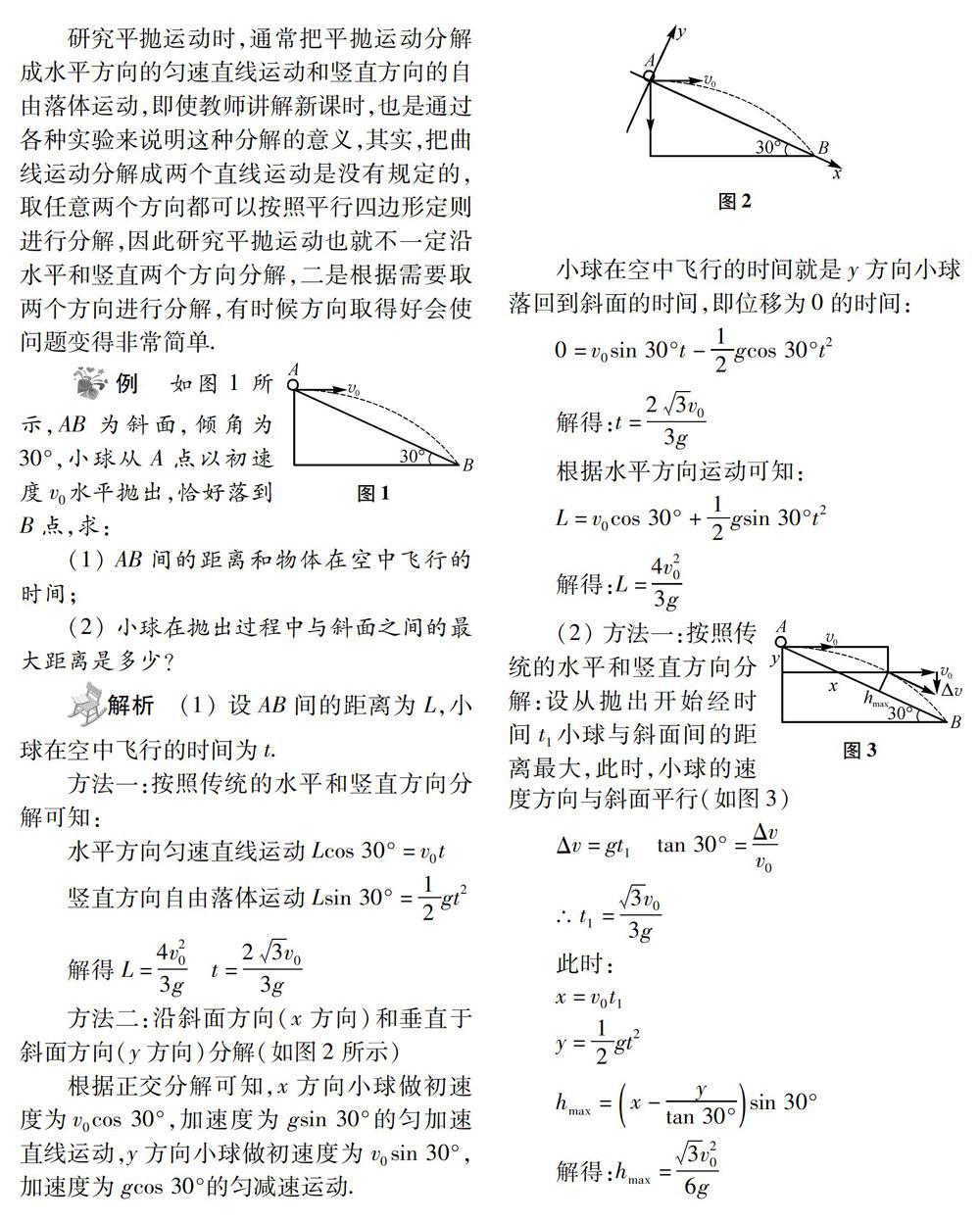
例 如图1所示，AB为斜面，倾角为30°，小球从A点以初速度v0水平抛出，恰好落到B点，求：

（1） AB间的距离和物体在空中飞行的时间：

（2）小球在抛出过程中与斜面之间的最大距离是多少？

解析 （1）设AB间的距离为L，小球在空中飛行的时间为t.

方法一：按照传统的水平和竖直方向分解可知：

方法二：沿斜面方向（x方向）和垂直于斜面方向（y方向）分解（图2所示）：

根据题意可知，小球离开斜面的距离即为y方向运动的位移，根据y方向运动可知，最大位移时y方向瞬时速度为零，根据运动方程直接得：

从本例可以看出，研究平抛运动时不一定沿水平方向和竖直方向分解运动，只要运用平行四边形定则，取任意两个方向都可以进行分解，也就是根据需要进行分解，在与斜面相关的问题中，巧妙选择分解的方法会使问题变得简单，在研究斜抛运动时分解方法同样是灵活的.

同样，研究斜抛运动问题也可以按照需求进行分解，如：

如图4所示，从A点以v0的初速度抛出一个小球，在离4点水平距离为s处有一堵高度为h的墙BC，要求小球能越过B点.问小球以怎样的角度抛出，才能使v0最小？

解析 方法一：将斜抛运动分解成v0方向的匀速直线运动和竖直方向的自由落体运动的合运动，如图5所示.

在位移三角形ADB在用正弦定理