牛顿运动定律中的图象问题

张统勋

通过图象解决问题是物理题的常见类型，也是一个难点.对于一些同学来说，总感到无从下手.现就牛顿运动中的三类图象题进行剖析，以期同学们能够更好地解决相关问题.

一、利用图象中的特征值求解

对于图象所提供的信息，可根据题目的需要从图象中找出特殊点的值来进行分析、应用.

例1 如图l（a）所示，质量m=1 kg的物体沿倾角θ=37°的固定粗糙斜面由静止开始向下运动，风对物体的作用力沿水平方向向右，其大小与风速v成正比，比例系数用k表示，物体加速度a与风速v的关系如图（b）所示.求：

（1）物体与斜面间的动摩擦因数μ；

（2）比例系数k.（sin 37°=0.6，cos 37°=0.8，g= 10m/是s2）

解析 （1）由图读出初始时刻，v=0，ao =4m/s2，对m受力分析有：

mgsinθ-μmgcosθ=mao

解得：μ=gsinθ-a0/gcosθ=0.25.

（2）对末时刻，v=5 m/s，a=0，受力分析有：

【变式训练1】一位蹦床运动员仅在竖直方向上运动，蹦床对运动员的弹力F随时间t的变化规律通过传感器用计算机绘制出来，如图2所示.设运动过程中不计空气阻力，g取10 m/s2.结合图象，试求：

（1）运动员的质量m；

（2）运动过程中，运动员的最大加速度；

（3）运动员离开蹦床上升的最大高度.

解析 （1）由前3.6 s的图象可知：运动员的重力G=500 N，则运动员的质量m=50 kg

（2）由图象知：最大弹力F_m=2 500N

根据牛顿第二定律：F_m-G= ma

得到最大加速度：a= 40 m/s2

（3）由题意，运动员在空中运动的时间：

t =8.4 s -6.8 s=1.6 s

下落时间：t= t0/2 =0.8s，则

运动员离开蹦床上升的最大高度

h=1/2gt2 =3.2 m

二、利用图象的面积计算

在匀变速直线运动中，我们利用v-t图象中的“面积”来计算物体运动的位移.涉及牛顿运动定律的应用中，不论是匀变速还是变速运动的情况，仍可用图象中的“面积”来计算位移.

例2 一质量为m=0.4kg的电动遥控玩具车在水平地面上做直线运动，如图3所示为其运动的v-t图象的一部分，已知0.4 s以前车做匀变速运动，之后做变加速运动直到速度最大，2 s时刻关闭发动机，玩具车开始做匀减速运动最终停止.小汽车全过程中所受阻力可视为恒定.

（1）关闭发动机后小车运动的时间；

（2）求匀加速阶段小汽车的驱动力；

（3）估算全过程小汽车行驶的距离.

【变式训练2】一颗子弹以水平速度v0穿透一块在光滑水平面上迎面滑来的木块后，二者运动方向均不变.设子弹与木块间相互作用力恒定，木块最后速度为v，则（）

A.v0越大，v越大

B.v0越小，v越大

C.子弹质量越大，v越大

D.木块质量越小，v越大

解析 由于子弹和木块间相互作用力恒定，因此在穿过木块的过程中，子弹和木块均做匀减速运动，v-t图象如图4线l、2所示，两图线与虚线和纵轴所围面积的大小即为木块的长度，若v0增大，图线如2、3所示，要保证图线所围面积不变，因此时间变短，v增大，选项A正确、B错误；子弹的质量越大，其加速度越小，图线如2、4所示，则相当于图线1、2，v增大，选项C正确；木块质量变小，木块的加速度增大，图线如1、5所示，相对于图线1、2，v变小，选项D错误.

答案 AC

三、利用图象分析多过程问题

对于牛顿第二定律和图象问题的分析，如果涉及多过程，需要分段分析运动情况.

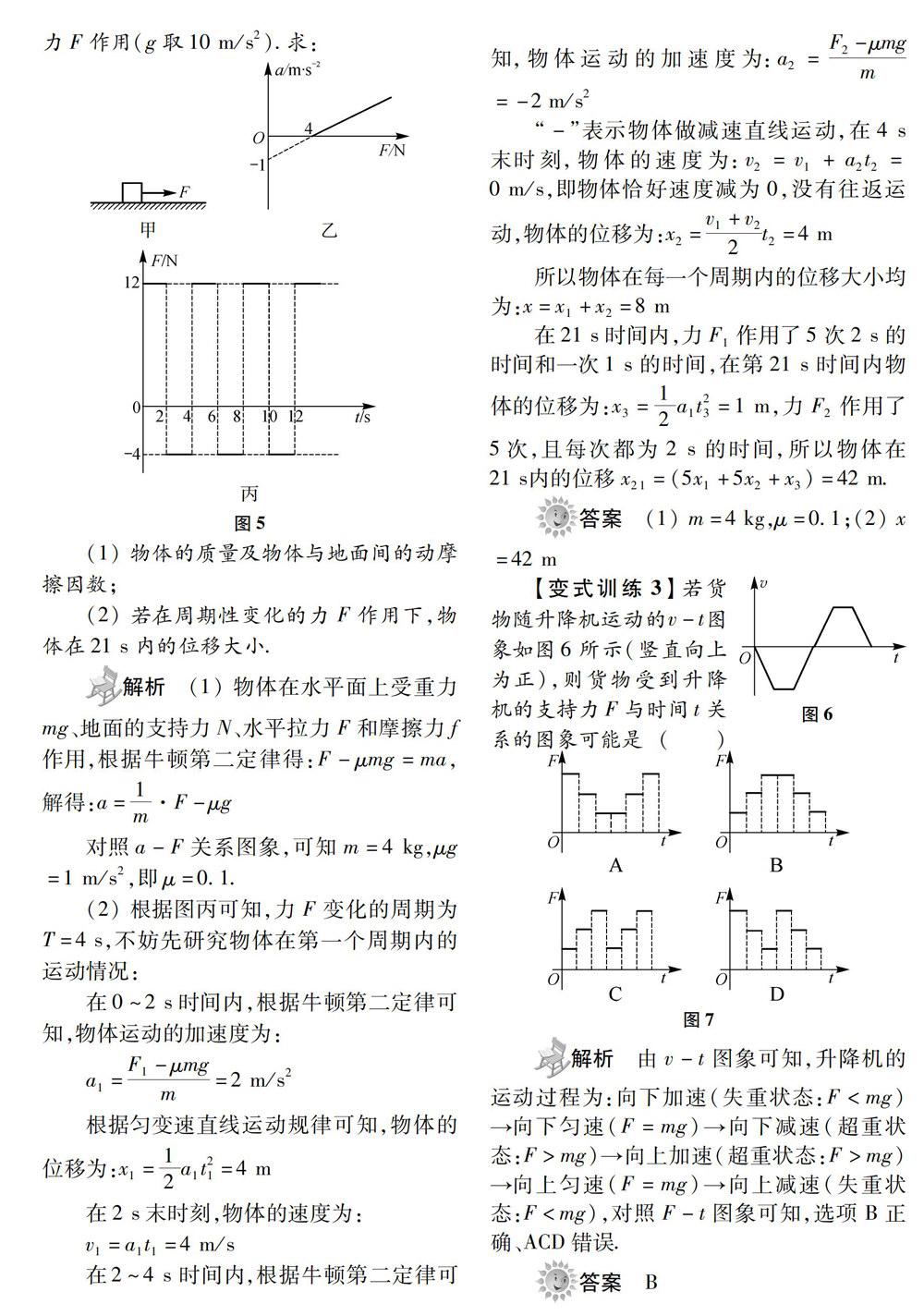
例3 一个物体放在足够大的水平地面上，图5甲中，若用水平变力拉动，其加速度随力变化图象为图5乙所示.现从静止开始计时，改用图5丙中周期性变化的水平力F作用（g取10m/S2）.求：

（1）物体的质量及物体与地面间的动摩擦因数：

（2）若在周期性变化的力F作用下，物体在21 s内的位移大小.

【变式训练3】若货物随升降机运动的v-t图象如图6所示（竖直向上为正），则货物受到升降机的支持力F与时间t关系的图象可能是（）

解析 由v-t图象可知，升降机的运动过程为：向下加速（失重狀态：F mg）→向上加速（超重状态：F> mg）→向上匀速（F= mg）→向上减速（失重状态：F< mg），对照F-t图象可知，选项B正确、ACD错误.

答案B