具时滞的微分新古典增长模型正周期解的存在性

张孟孟 赵前进

（安徽理工大学数学与大数据学院 安徽淮南 232001）

近年来，随着市场经济的发展，对市场经济模型的研究已经成为数学经济学中广泛讨论的课题，其中对经济增长模型的定性和稳定性分析引起诸多经济学家和数学家的广泛关注和研究。例如，在文献[1,2]中，Day最初研究了一类新古典增长模型、生产力和人口增长模型，研究表明即使在简单的经济结构下，也会有复杂的动力学行为出现。此后，关于复杂经济动力学的研究得到了越来越多的重视，参见[3-5]及相关参考文献。

正如Matsumoto与Szidarovszky在文献[6]中所述，为了更好地描述经济的长时间行为，根据经济学原理，建立新经济古典增长模型，主要基于如下两个假设：一是劳动力和资本的充分利用，二是输出市场的及时调整。由于生产函数的合理选择，模型的稳态解通常是渐近稳定的。然而，在现实世界中，经济学家观察到经济增长路径往往表现出持久震荡性。因此，当非线性项和生产时滞都存在的情况下，为更好地描述这种持久行为是如何出现的，新古典增长模型将成为一个很好的研究出发点。基于这一事实，Matsumoto与Szidarovszky在文献[9]中提出了如下具有丘型生产函数的增长模型:

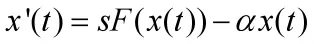
其中x是每个劳动力的资本，s∈（0，1）是平均储蓄倾向，对于α=k+sμ，μ是资本的折旧率，k是劳工的增长率；丘型函数（a，b和 A是正系数）是Cobb-Douglas式的，其中反映了由人均输出造成的污染影响。考虑到在经济市场实现的过程中，时间上造成的延迟是不可避免的，同时还会受到自然环境和人为因素的影响，他们在文献[6]中进一步提出了如下形式的经济模型：

τ是运转过程中产生的时滞，n可以被看作是测量生产函数规模的一个指标，δ反映了资本日益集中导致的“负面效应”的强度，并由自然环境或能源资源的破坏性程度决定。显然模型(1)是具有常时滞的一种具有非单调双稳态非线性的时滞微分方程，其具有两个正平衡的吸引域和唯一不稳定正平衡的收敛性，在黄创霞和郑作环教授等的文献[7,8]中得到了验证。最近，当0＜n＜1时，利用压缩映射原理和Lyapunov方法，段炼和黄创霞研究了如下非自治具有多时滞的微分新古典增长模型的概周期解的存在性和全局吸引性:

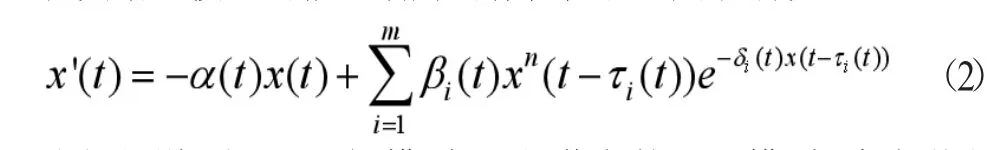
我们知道，当n=1时，模型（2）是著名的果蝇模型，诸多学者围绕该模型展开了深入的研究，在其周期动力学方面已经取得了很好的成果，例如文献[10-13]。然而，在n＞1的情况下，鲜有对模型（2）正周期解存在性的研究。

基于以上讨论，我们利用微分不等式技巧和锥不动点定理，研究模型（2）在n＞1的情况下其正周期解的存在性。为了方便，我们首先给出如下假设：和都是T周期函数，其中i=1,2…，m，并记。

一、预备知识

在这一部分，我们给出在本文中运用到的记号、定义和引理。对于一个连续的正T周期函数f（t），定义为为

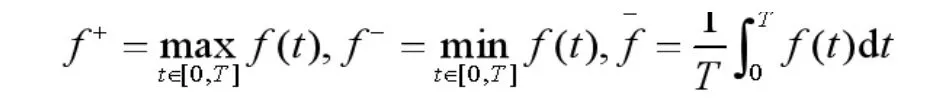
我们取初始条件

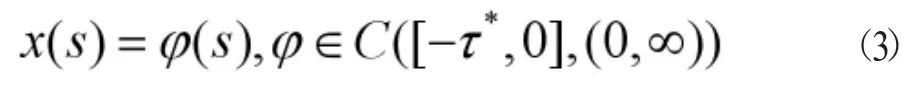
这里 τ*=max τi+容易证明初值问题（2）和（3）在 t∈[0,∞]上有一个非负解 x（t）且对于 t≥τ* 有 x（t）＞0。

定义1 令X是一个Banach空间，P是X的一个非空闭集。若有

（1）对任意的 x，y∈P，a，b≥0 都有 ax+by∈P，

（2）当x,-x∈P时，x=0成立，则称P是X的一个锥。

引理1（Krasnosekill锥不动点定理[14]）设X是一个Banach空间，P⊂X是X中的一个锥。Ω1和Ω2是X中的开闭集且令

（1） 对 x∈P∩∂Ω1，有 ||AX||≥||x||；对 x∈P∩∂Ω2，有||AX||≤||x||；或者

（2） 对 x∈P∩∂Ω1，有 ||AX||≤||x||；对 x∈P∩∂Ω2，有||AX||≥||x||成立，则 A在 P∩上必有不动点。

二、主要结果

则x在赋予范数||·||下为Banach空间。若x(t)∈X是方程（2）的一个正周期解，则有

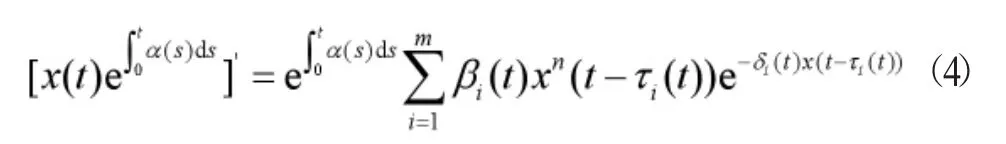
对（4）式两边在[t,t+T]上积分可得

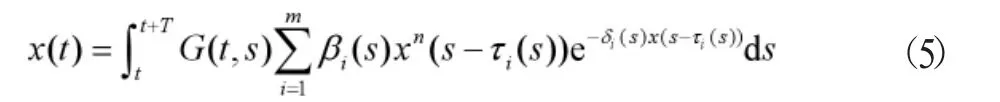
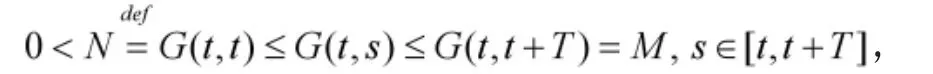
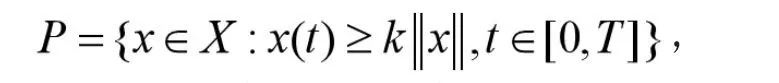
显然P是X的一个锥。定义算子A:X→X，则

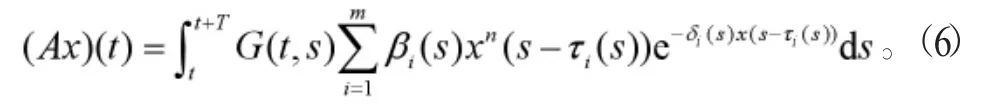
对于 X∈P,t∈[O,T]，有

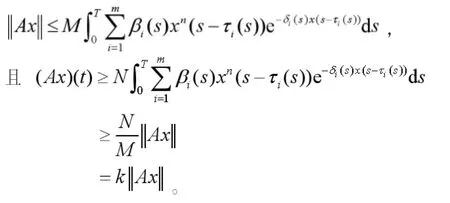
因此，AP⊂P。

引理2 假设（H）成立，则A：P→P是全连续的。

证明 显然，A在[1，∞]是连续的且对任意地X∈P,t∈R+有

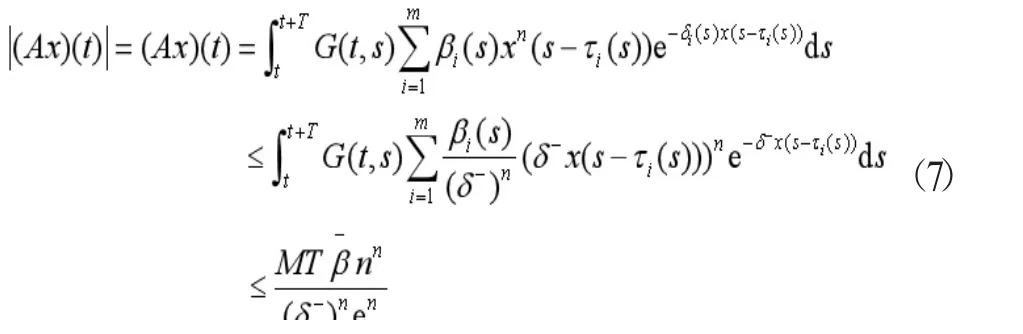
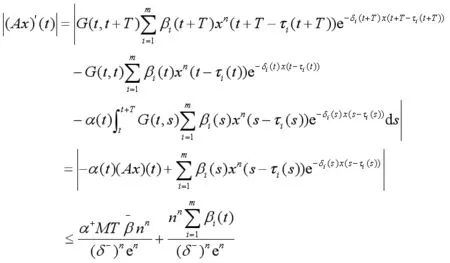
因此，{Ax：x∈P}是一类一致有界且等度连续的函数。由Ascoli-Arzela定理可知A:P→P，具有紧性，继而，A:P→P是全连续的。引理2得证。

引理3 假设（H）成立，令

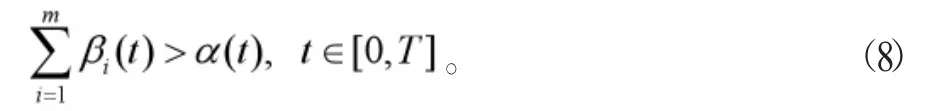
则对于任意的x∈P，存在正常数A，B使得下列不等式成立

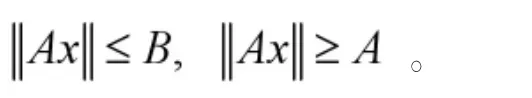
证明 由（7）知，对于任意的 x∈P，t∈R+有

由（8）成立，则可以找到一个适当的γ＞1使得下列不等式成立

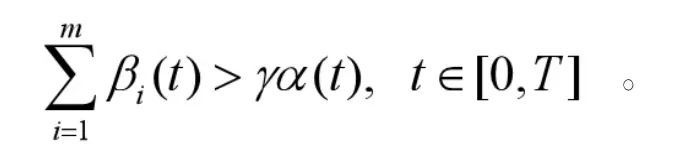
对于任意的 x∈P，t∈R+，有

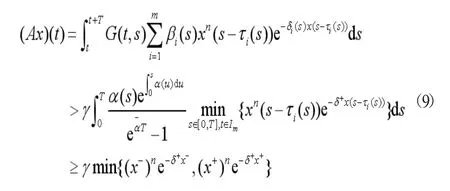
比较（5）和（6）两式可知，对于任意的 x∈P，t∈R+，我们有

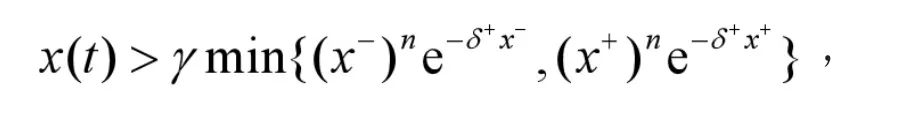
这就意味着

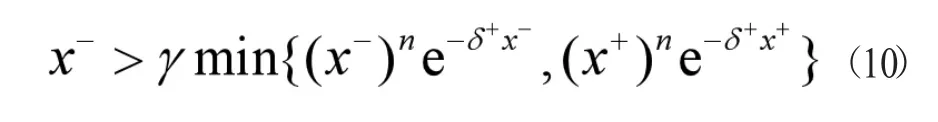
根据（7）同理可得，x（t）≤B，这就意味着 x+≤B。

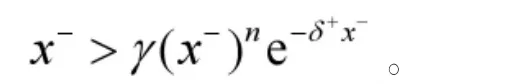
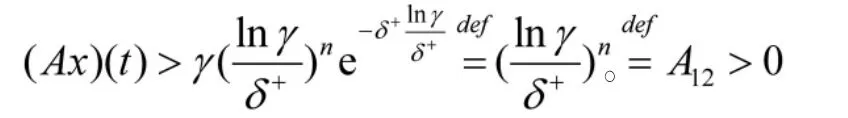
三、应用举例

考虑如下具时滞的微分新古典增长模型

注记 本文中，我们考虑了时所考虑模型周期解的存在性。由于时，周期解可作特殊概周期解来研究，文献[5]已建立了很好的充分条件并验证了概周期解的存在性。我们知道，当时，模型(2)是著名的Nicholson果蝇模型，学者围绕该模型展开了深入的研究，在其周期解存在性的充分条件上已经取得了很多成果。据作者所知，对一类具时滞的微分新古典增长模型关于的周期解存在性的研究还很少见，因此本文的结论推广并补充了已有文献的结果。本文我们只研究了模型(2)周期解存在性的充分条件，对其感兴趣的学者还可继续研究其稳定性和全局吸引性的相关结论。

四、结语

本文利用微分不等式技巧和锥不动点理论验证了一类具时滞的微分新古典增长模型正周期解的存在性，判据新颖改进并推广了已有文献的相关结论，同时为经济学工作者提供了强有力地理论依据。