基于颗粒流理论的微灌砂滤层反冲洗过程砂粒速度场模拟
李景海,刘清霞,翟国亮,蔡九茂,张文正
基于颗粒流理论的微灌砂滤层反冲洗过程砂粒速度场模拟
李景海1,刘清霞1,翟国亮2※,蔡九茂2,张文正2
(1.安阳工学院土木与建筑工程学院,安阳 455000; 2. 中国农业科学院农田灌溉研究所,新乡 453002)
砂颗粒流在石英砂滤层反冲洗流场中的速度分布,对滤层流化状态的稳定性和反冲洗效果起决定性作用。为了对滤层反冲洗过程砂颗粒的速度场进行分析,并确定最佳反冲洗速度,该文以厚度为400 mm,粒径范围为1.0~1.18 mm的石英砂滤层为研究对象,基于颗粒流运动理论,采用Eulerian-Eulerian模型对滤层反冲洗过程砂粒的速度场进行3维动态模拟。为了验证模拟结果的准确性,作者开展了室内模型试验,并将模拟结果与试验结果进行对比,结果显示,滤层膨胀高度的最大模拟误差为9.8%,能够控制在10%以内,说明数值模拟结果是可信的。在此基础上,分析了反冲洗流化倍数为1.3、1.5、1.7和1.9时,滤层高度分别为15、25和35 cm 3个横截面上,在不同的反冲洗时间,砂粒的轴向速度沿横坐标的分布规律。根据砂粒在3个横截面上运动速度的大小和方向,判断砂滤层是否达到完全流化;根据砂粒在3个横截面上运动趋势是否一致,砂粒的上升区是否保持稳定,判断滤层流化状态是否稳定。结果显示,当反冲洗流化倍数不小于1.7时,滤层才能达到稳定的流化状态,从而达到比较理想的反冲洗效果,并得出滤层最佳反冲洗流化倍数为1.7。研究结论为砂过滤器的反冲洗研究提供了理论基础和技术支撑,为反冲洗性能参数的确定提供了参考。
模型;计算机仿真;灌溉;石英砂滤层;反冲洗;多相流
0 引 言
砂过滤器是微灌系统最常用的过滤功能最佳的水处理设备。对砂过滤器过滤性能的研究无疑十分必要,但为了实现滤料的再生,砂滤层的反冲洗也至关重要。目前对砂滤层反冲洗的研究主要以试验为主。翟国亮等[1-3]研究了砂滤层反冲洗速度与反冲洗时间的关系,测定了砂过滤器反冲洗参数。邓忠等[4-5]研究了反冲洗水颗粒粒径的变化规律。冯俊杰等[6-7]对以水压为驱动力的砂过滤器三向阀进行了力学计算。张文正等[8-9]对砂滤层加气反冲洗进行了研究,得出了气水合理比例与反冲洗时间。
试验研究主要从宏观层面对砂滤层性能进行了分析,而数值模拟方法在大量减少试验工作量的同时,可以得到与试验研究相同的效果,同时更侧重于微观尺度的研究,通过对滤层流场的分析,可以得到滤层压力、滤层高度、孔隙率、颗粒速度等参数的分布特性,为砂过滤器研究提供基础理论。在砂过滤器数值模拟方面,刘文娟[10]对砂过滤器反冲洗进行了二维稳态模拟,但没有将砂滤层的反冲洗做为一个动态平衡过程。Bové等[11-12]等研制了一种新型滤帽,减少了过滤的压降损失,并采用CFD模拟软件对过滤器水头损失进行了模拟,但没有研究砂滤层的特性。作者对石英砂滤层反冲洗过程进行了多相流动态模拟,研究了滤层压降、密度和水体积分数的变化规律,并得出了反冲洗速度的合理范围[13-14],但目前没有对造成滤层参数变化的动力学原因进行研究。
砂颗粒在滤层中的运动特性,是造成滤层压降、密度和水的体积分数等参数变化的直接原因。为了从动力学的角度对砂滤层运动特性进行分析,本文在前期研究的基础上[15-17],将颗粒流理论与Eulerian-Eulerian模型相结合,建立了砂滤层反冲洗数学模型,采用Ansys14.5模拟软件,对石英砂滤层反冲洗过程进行多相流动态模拟,并根据试验数据验证模拟结果的可靠性。在此基础上,选取滤层上中下3个典型过滤截面,绘制3个截面上砂粒的速度分布图,对砂颗粒运动速度的分布情况进行分析,根据3个截面上砂颗粒运动速度是否一致,判断滤层是否达到稳定流化状态,并找出滤层达到稳定流化状态所对应的反冲洗速度,最终得出最佳反冲洗速度。为砂过滤器的研究提供基础理论与研究方法,为反冲洗性能参数的确定提供参考数据。
1 石英砂滤层反冲洗试验
试验在中国农业科学院农田灌溉研究所进行,为室内模型试验,试验模型见图1。过滤器采用透明有机玻璃管制作,管内径200 mm、高1 200 mm,玻管下端安装3个滤帽,用于防止滤料从过滤器漏出,并均匀分布反冲洗水。以石英砂为滤料,砂粒径范围为1.0~1.18 mm,当量粒径为1.06 mm。石英砂滤料放置于过滤器内部,滤层厚度为400 mm。试验时,利用水泵将清水从反冲洗进水口注入过滤器模型,采用涡轮流量计(LWGY-25,精度为0.5级)测反冲洗流量,根据反冲洗流量,计算反冲洗速度。测量并记录各反冲洗速度对应的滤层膨胀高度。

图1 试验装置示意图
2 石英砂滤层反冲洗动力学模拟
2.1 模拟模型建立
微灌石英砂滤层的反冲洗过程是由水和石英砂组成的固液两相流体系,采用Eulerian-Eulerian模型[18-20]能够较准确的模拟其内部流场。由于石英砂在反冲洗过程中,形成了流化的颗粒群,在对石英砂颗粒的速度场进行模拟时,为了准确描述颗粒的受力和运动情况,将颗粒流运动理论与Eulerian-Eulerian模型相结合,得到反冲洗模拟模型。
连续性方程和动量方程分别根据质量守恒和动量守恒定理得到[21]。
连续性方程:

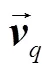
对液相和固相分别建立动量方程,液相的动量方程为
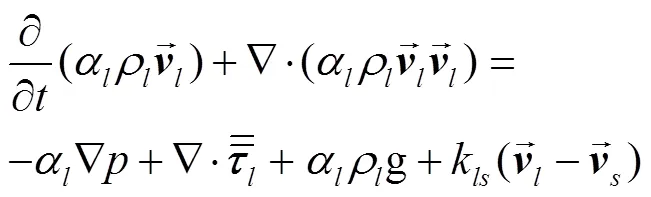
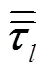
固相的动量方程为
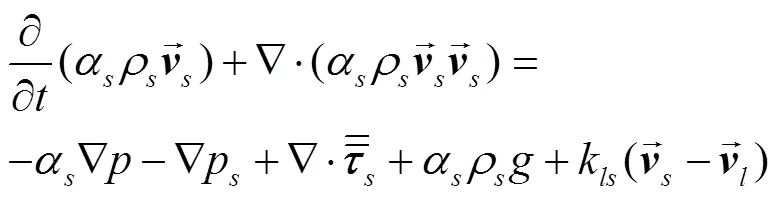
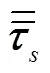
压力应变张量的表达式为
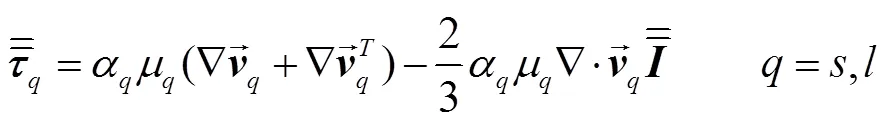
石英砂的粘度系数为
µ=µ,c+µ,k+µ,f(5)
式中µ,c为碰撞粘度系数(Pa·s);µ,k为动力粘度系数(Pa·s);µ,f为摩擦粘度系数(Pa·s)。
当石英砂处于流化状态时,颗粒之间的摩擦系数µ,f可不考虑,即
µ,f=0 (6)
碰撞粘度系数µ,c见式(7)[22]
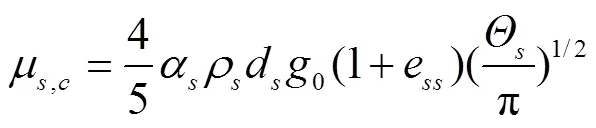
式中d为石英砂颗粒的平均粒径,m;Θ为颗粒温度,℃;e为颗粒碰撞的归还系数;0为径向分布函数[23],表达式为
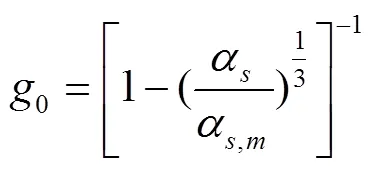
式中α为固相体积分数的最大值,因为在球形颗粒紧密堆积时,体积分数最大,为0.63。
动力粘度系数µ,k见式(9)[24]。
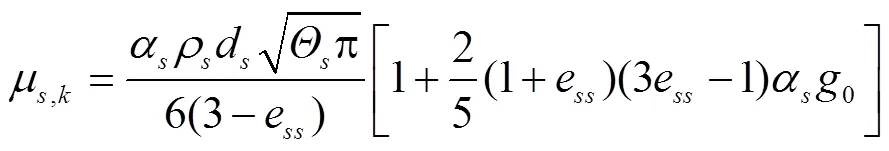
固相压力为
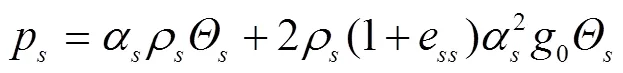
颗粒温度计算方程见式(11)[25]。
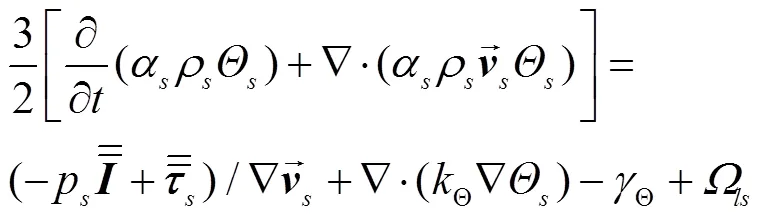
式中Θ为能量扩散系数。
Ω为液相波动能量与固相波动能量之间的交换量[22],其表达式见式(12)
Ω=−3kΘ(12)
液固交换系数k见式(13)[26]。
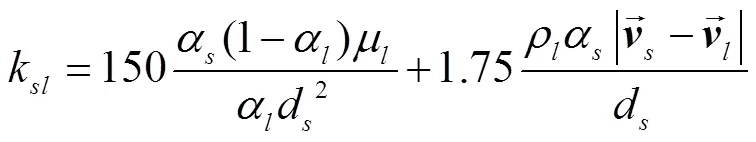
γ为颗粒流波动能量的耗散项[27],表达式见式(14)。
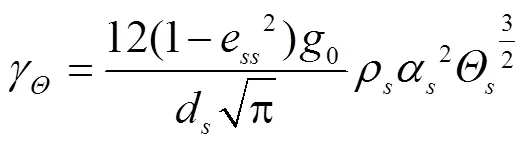
2.2 几何模型及算法设置
采用Gambit软件建立几何模型,过滤器几何模型与细部结构见图2。
以Eulerian-Eulerian模型为多相流模拟模型,进行瞬态求解。定义液相为水,固相为砂。选用Gidaspow曳力函数,颗粒温度设为常温,压力速度耦合方程采用PC-SIMPLE算法求解。选用每一相的湍流模型,采用Green-Gauss方程进行空间离散化,动量、湍动能、湍流耗散率和体积分数方程均采用一阶迎风格式。进口边界设为速度进口,为模拟时采用的反冲洗速度;出口边界设为压力出口,压力为一个大气压。以速度进口对流场进行初始化。采用模拟软件Ansys14.5进行数值计算,参数设置如表1所示。
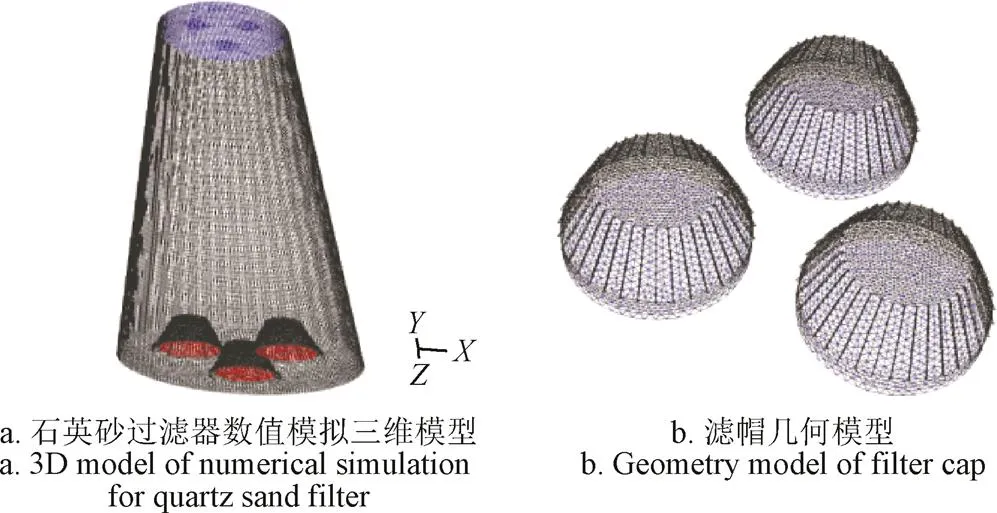
图2 过滤器几何模型

表1 数值模拟参数
3 数值计算结果分析
3.1 滤层反冲洗模拟的试验验证
由于滤层砂粒的轴向速度直接影响到滤层反冲洗膨胀高度,因此,采用滤层膨胀高度的试验值对模拟结果进行验证。根据入口的反冲洗流速,由CFD软件对反冲洗过程进行模拟,得到滤层的膨胀高度。绘出滤层膨胀高度随反冲洗速度的变化关系图并与试验值进行对比(图3)。
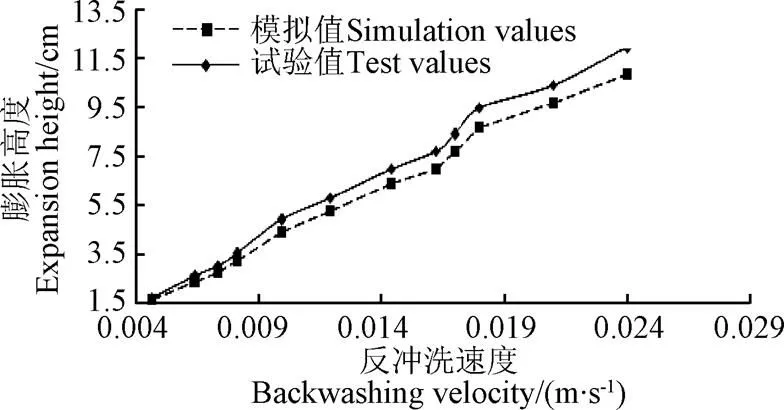
图3 滤层膨胀高度模拟值与试验值对比
将滤层膨胀高度的试验值与模拟值对比可知,滤层膨胀高度的最大误差为9.8%,因为滤层最大膨胀高度的模拟值为10 cm,9.8%的误差对应的绝对误差只有0.98 cm,误差在可以接受的范围。结果说明,滤层膨胀高度试验值与模拟值能够较好地吻合,模拟结果准确可信。
以v表示滤层最小反冲洗流化速度。选取1.3v、1.5v、1.7v、1.9v共4个反冲洗速度对滤层砂粒的时均轴向速度分布规律进行分析。根据试验观察,这4个反冲洗速度代表了滤层从流化状态不稳定到逐步稳定的过程,具有较强的代表性。
3.2 滤层横截面砂颗粒轴向速度分布规律分析
在滤层中依次选取高度为15、25和35 cm的3个横截面,分别代表了滤层的底部、中部和上部位置,在不同的反冲洗时间,绘制4个反冲洗速度对应的砂颗粒的时均轴向速度在截面沿横坐标的分布图(图4)。
当反冲洗水流通过滤层时,在水流作用下,砂粒逐渐松动,颗粒间空隙增大,滤层体积开始膨胀。随着水流的持续反冲洗,滤层将不能维持固定状态,颗粒全部悬浮于流体中,显示出不规则的运动。随着反冲洗流速的增加,颗粒的运动加剧,滤层的膨胀也随之增大,滤层的这种状态称为流化状态。在图4中,当砂粒有了明显的运动速度时,就可以判定为滤层产生了流化现象。
对于所选的4个反冲洗速度,作者分别考查了滤层在5、10、15、20、25、30、35和40 s时,15、25、35 cm 3个截面上砂粒速度沿横轴的分布规律,并找出了滤层达到完全流化的临界时间。
在图4a中,即反冲洗流化倍数为1.3时,当反冲洗时间达到30 s时,上部的砂粒开始有了明显的上升运动,运动速度位于−0.3~0.1 m/s之间,可以判断整个滤层达到了完全流化状态。滤层流化后,以反冲洗时间为40 s为例,可以看出,在同一个反冲洗时间,砂粒在3个横截面上轴向速度的运动趋势不同步,底部颗粒在向上运动的过程中,最大运动速度在横轴上的位置不断变化,由此可知,砂颗粒在运动过程中遇到了阻力,运动方向发生了变化,也说明砂粒的运动没有稳定的路线,滤层处于不稳定流化状态;在图4b中,即反冲洗流化倍数为1.5时,当反冲洗时间达到25 s时,在=35 cm的截面上,砂粒开始有了明显的上升运动,运动速度位于−0.14~0.1 m/s之间,可以判断整个滤层达到了完全流化状态。同时,滤层完全流化后,上升颗粒在横轴位置仍然不稳定,最大速度向边壁发生转移,说明滤层的流化状态仍不稳定;在图4c中,即反冲洗流化倍数为1.7时,当反冲洗时间达到20 s时,在=35 cm的截面上,砂粒开始有了明显的上升运动,运动速度位于−0.26~0.3 m/s之间,可以判断整个滤层达到了完全流化状态。同时,由反冲洗时间为20与25 s图的对比可知,3条曲线的变化趋势基本一致,说明滤层在3个横截面上砂粒的运动趋势基本相同,滤层达到了稳定的流化状态。流化稳定后的滤层,右侧的颗粒形成上升区,左侧的颗粒形成下降区,整个滤层形成一个逆时针方向的环流区,砂粒在环流区中循环往复,形成了稳定的运动路径;在图4d中,即反冲洗流化倍数为1.9时,当反冲洗时间达到15 s时,上部的砂粒开始有了明显的上升运动,运动速度位于−0.17~0.69 m/s之间,说明整个滤层达到了完全流化状态。3个横截面上砂粒的运动趋势基本相同,在整个的反冲洗过程中,砂粒的上升区处于滤层的右半部,颗粒的下降区位于左侧,整个滤层形成一个稳定的环流区,砂粒在环流区中循环往复,形成了稳定的运动路径。
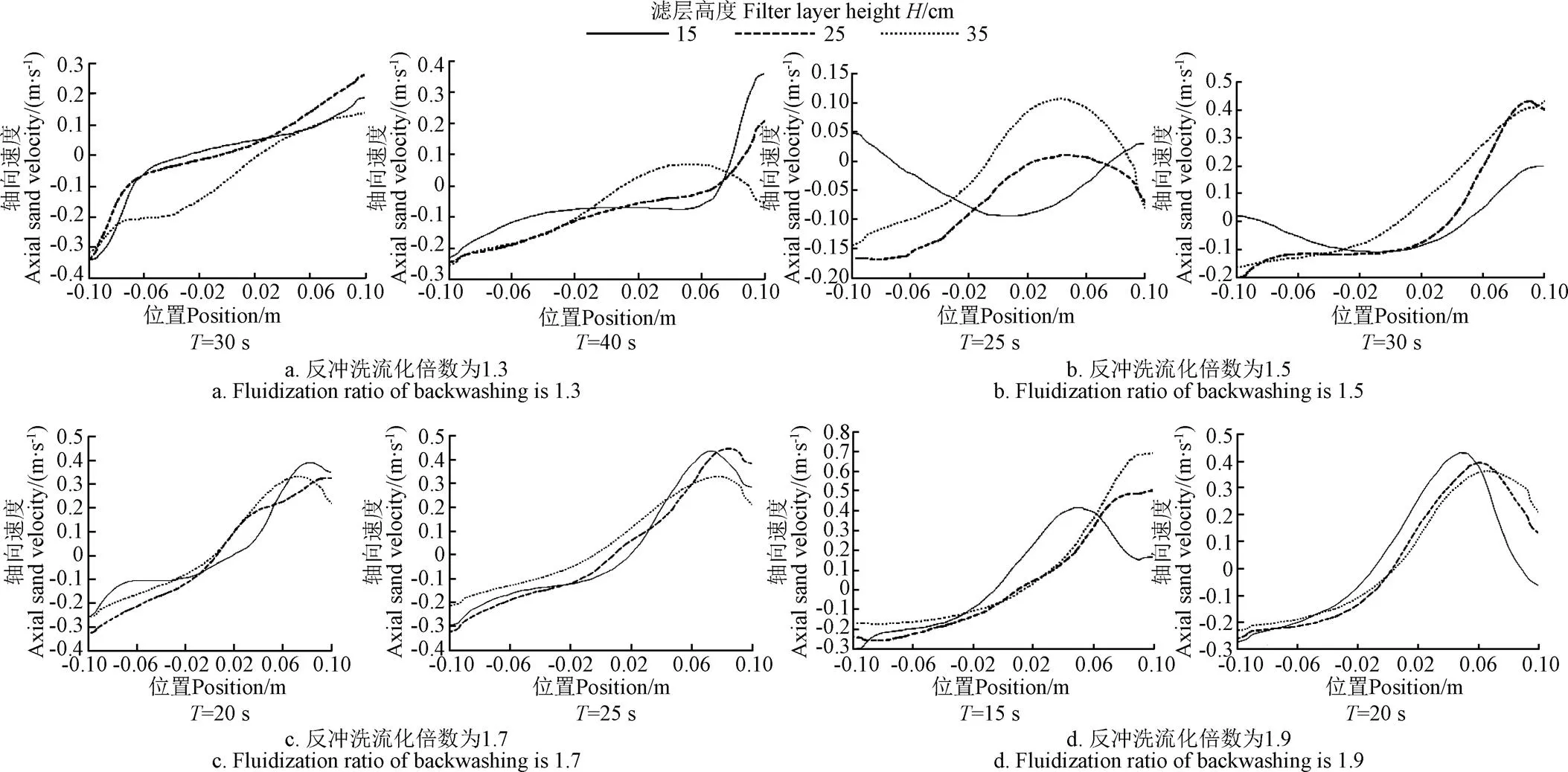
注:T为反冲洗时间;横坐标原点为截面圆心。 Note: T is backwashing time; Origin of the transverse coordinate is center of cross section.
由以上分析知,当滤层达到稳定的流化状态后,砂颗粒会形成一个稳定的环流区,并在环流区中循环往复,砂粒在反复的循环过程中得到冲洗。形成环流区的原因在于,反冲洗水在上升过程中,受到砂滤层的阻力而改变方向,当水流到达边壁时,又受到边壁的阻力,从而又向上运动并最终到达滤层顶部。水流在运动过程中,携带砂粒一起运动,当砂粒随水流到达滤层顶部后,水流速度变缓,砂粒在重力作用下开始下降,从而形成砂粒环流区。
当滤层达到稳定的流化状态后,才会有较好的反冲洗效果,根据前期研究知,砂滤层临界反冲洗流化倍数为1.7[14],流化倍数超过1.7时,反冲洗效果也会变差,因此最佳反冲洗速度为1.7v,最佳反冲洗流化倍数为1.7。
拟合滤层达到完全流化状态的时间与反冲洗流化倍数的关系曲线如图5所示,其表达式见式(15)。
−2562.5 (15)
式中滤层达到完全流化状态的时间与反冲洗流化倍数的决定系数2为1,说明滤层达到完全流化状态的时间与反冲洗流化倍数呈负线性关系,即反冲洗速度越大,滤层达到完全流化所用的时间越短。
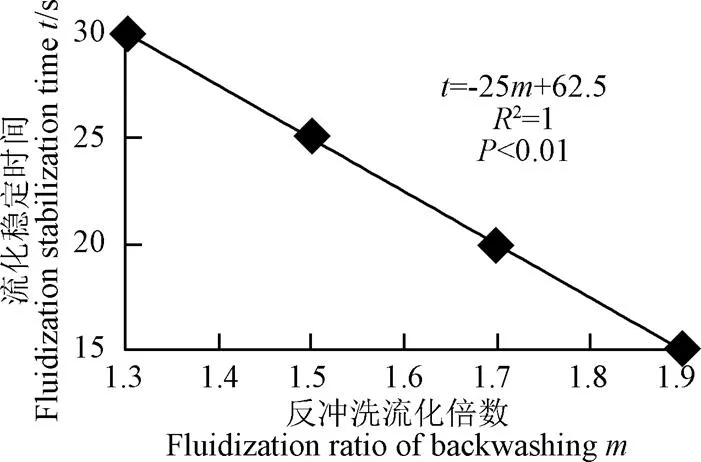
图5 流化稳定时间与反冲洗流化倍数关系
4 结 论
本文以Eulerian-Eulerian模型为基本方程,结合水和石英砂所组成的两相流的特征,建立了水砂分别为液相和固相的液固两相流模拟模型。采用颗粒流运动理论进行封闭,封闭方程有压力应变张量方程、石英砂的粘度系数方程、径向分布函数、固相压力方程、颗粒温度计算方程、液固交换系数方程和能量的耗散方程等。通过对模拟结果分析,得到以下结论:
1)对砂颗粒沿横轴的分布规律进行了动态模拟,并且通过室内试验对模拟结果进行了验证,模拟值与试验值误差为9.8%,表明数值模拟结果准确可信;
2)滤层达到稳定的流化状态后,砂颗粒会形成一个稳定的环流区,并在环流区中循环往复。并得到滤层最佳反冲洗流化倍数为1.7;
3)滤层达到完全流化状态的时间与反冲洗流化倍数呈负线性关系,即,在砂颗粒不被水流冲出过滤器的前提下,反冲洗速度越大,滤层达到完全流化所用的时间越短。
采用Eulerian-Eulerian模型模拟砂滤层的反冲洗过程,需要选用合适的封闭方程。对不同流场的瞬态模拟,所需要增加的源项不同。本文对速度流场进行模拟,所选用的封闭方程,与前期研究所选用的封闭方程有所不同,因而对压降、密度等的模拟结果误差可能会偏大。因而需要对Eulerian-Eulerian模型进行修正,使该模型能够比较全面的模拟砂滤层的反冲洗过程。在后期研究中,作者将对模拟模型中固液交换系数进行修正,使模型能够更好的适用于微灌砂滤层的反冲洗模拟。
[1] 翟国亮,陈刚,赵武,等. 微灌用石英砂滤料的过滤与反冲洗试验[J]. 农业工程学报,2007,23(12):46-50.
Zhai Guoliang, Chen Gang, Zhao Wu, et al. Experimental study on filtrating and backwashing of quartz sand media in micro-irrigation filter[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2007, 23(12): 46-50. ( in Chinese w ith English abstract )
[2] 翟国亮,冯俊杰,邓忠,等. 微灌用砂石过滤器反冲洗参数试验[J]. 水资源与水工程学报,2007,18(1):24-28.
Zhai Guoliang, Feng Junjie, Deng Zhong, et al. Parameters experiment of backwashing on sandy filter in micro-irrigation[J]. Journal of Water Resources & Water Engineering, 2007, 18(1): 24-28. (in Chinese w ith English abstract)
[3] 赵红书. 微灌用石英砂滤料的过滤与反冲洗性能研究[D]. 北京:中国农业科学院,2010.
Zhao Hongshu. Performance of Filtration and Flushing of Quartz Sand Media for Micro-Irrigation[D]. Beijing: Chinese Academy of Agricultural Sciences, 2010. (in Chinese with English abstract)
[4] 邓忠,翟国亮,仵峰,等. 微灌过滤器石英砂滤料过滤与反冲洗研究[J]. 水资源与水工程学报,2008,19(2):34-37.
Deng Zhong, Zhai Guoliang, Wu Feng, et al. Study on the filtration and backwashing for the quartz filter in micro-irrigation[J]. Journal of Water Resources & Water Engineering, 2008, 19(2): 34-37. (in Chinese with English abstract)
[5] 邓忠,翟国亮,宗洁,等. 浑水质量分数对石英砂滤料过滤性能的影响[J]. 排灌机械工程学报,2013,31(11):1007-1012.
Deng Zhong, Zhai Guoliang, Zong Jie, et al. Influence of muddy water mass fraction on performance of packed quartz sand bed[J]. Journal of Drainage and Irrigation Machinery Engineering, 2013, 31(11): 1007-1012. (in Chinese with English abstract)
[6] 冯俊杰,翟国亮,邓忠,等. 微灌过滤器用水压驱动反冲洗阀启闭机构的力学计算[J]. 农业机械学报,2007,38(12):212-214.
Feng Junjie, Zhai Guoliang, Deng Zhong, et al. Mechanical calculation of opening and closing mechanism of back flushing valve driven by hydraulic pressure[J]. Transactions of the Chinese Society for Agricultural Machinery, 2007, 38(12): 212-214. (in Chinese with English abstract)
[7] 蔡九茂,李莉,翟国亮,等. 3种微灌砂过滤器水动三向阀性能比较试验研究[J]. 排灌机械工程学报,2017,35(7):596-601.
Cai Jiumao, Li Li, Zhai Guoliang, et al. Comparative experiment on performance of three hydrodynamic three-way valves in microirrigation sand filter[J]. Journal of Drainage and Irrigation Machinery Engineering, 2017, 35(7): 596-601. (in Chinese with English abstract)
[8] 张文正,翟国亮,邓忠,等. 微灌砂滤料的表层过滤和气水反冲洗试验研究[J]. 灌溉排水学报,2013,30(1):86-90.
Zhang Wenzheng, Zhai Guoliang, Deng Zhong, et al. Surface filtration and air-water backwashing for sandy filter media in micro-irrigation[J]. Journal of Irrigation and Drainage, 2013, 30(1): 86-90. (in Chinese with English abstract)
[9] 张文正. 微灌砂滤层气水反冲洗与过滤的试验研究[D]. 北京:中国农业科学院,2013.
Zhang Wenzheng. Experiment Research of Air Water Backwashing and Filtration of Sand Layer in Micro-Irrigation[D]. Beijing: Chinese Academy of Agricultural Sciences, 2013. (in Chinese with English abstract)
[10] 刘文娟. 石英砂过滤器过滤及反冲洗特性的实验研究与数值模拟[D]. 北京:中国农业科学院,2014.
Liu Wenjuan. Experimental Study and Numerical Simulation of Filtration and Backwashing Characteristics of Quartz Sand Filter[D]. Beijing: Chinese Academy of Agricultural Sciences, 2014. (in Chinese with English abstract)
[11] Bové J, Puig-Bargues J, Arbat G, et al. Development of a new underdrain for improving the efficiency of microirrigation sand media filters[J]. Agricultural Water Management, 2017, 179: 296-305.
[12] Bové J, Arbat G, Pujol T, et al. Reducing energy requirements for sand filtration in microirrigation: Improving the underdrain and packing[J]. Biosystems Engineering, 2015, 140: 67-78.
[13] 李景海,翟国亮,黄修桥,等. 微灌石英砂过滤器反冲洗数值模拟与流场分析[J]. 农业工程学报,2016,32(9):74-82.
Li Jinghai, Zhai Guoliang, Huang Xiuqiao, et al. Numerical simulation and flow field analysis of backwashing of Quartz sand filter in micro irrigation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2016, 32(9): 74-82. (in Chinese with English abstract)
[14] 李景海,蔡九茂,翟国亮,等. 基于砂滤层内水体积分数瞬态模拟的反冲洗速度优选[J]. 农业工程学报,2018,34(2):83-89.
Li Jinghai, Cai Jiumao, Zhai Guoliang, et al. Optimization of backwashing speed based on transient simulation of the volume fraction of water in the sand filter layer[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(2): 83-89. (in Chinese with English abstract)
[15] 李景海. 微灌石英砂滤层清洁压降分形阻力模型与反冲洗数值模拟[D]. 北京:中国农业科学院,2016.
Li Jinghai. Fractal Resistance Model of Clean Pressure Drop and Numerical Simulation of Backwashing Process of Quartz Sand Filter Layer in Micro-Irrigation[D]. Beijing: Chinese Academy of Agricultural Sciences, 2016. (in Chinese with English abstract).
[16] 李景海,刘清霞,黄修桥,等. 微灌石英砂滤层流态特性与分形阻力模型参数确定[J]. 农业工程学报,2015,31(13):113-119.
Li Jinghai, Liu Qingxia, Huang Xiuqiao, et al. Flow state characteristics and fractal model parameters determination of quartz sand filter layer used in micro-irrigation[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2015, 31(13): 113-119. (in Chinese with English abstract).
[17] 李景海,刘清霞,黄修桥,等. 微灌石英砂滤层清洁压降计算参数确定与分析[J]. 灌溉排水学报,2016,35(11):24-28.
Li Jinghai, Liu Qingxia, Huang Xiuqiao, et al. Determination and analysis of the calculation parameters for the cleaning pressure drop of quartz sand filter layer used in micro-irrigation[J]. Journal of Irrigation and Drainage, 2016, 35(11): 24-28. (in Chinese with English abstract)
[18] 贺靖峰. 基于欧拉-欧拉模型的空气重介质流化床多相流体动力学的数值模拟[D]. 北京:中国矿业大学,2012.
He Jingfeng. Numerical Simulation of Multiphase Fluid Dynamic in Air Dense Medium Fluidized Bed Based on Euler-Euler Model[D]. Beijing: China University of Mining and Technology, 2012. (in Chinese with English abstract)
[19] 贺靖峰,赵跃民,何亚群,等. 基于Euler-Euler模型的空气重介质流化床密度分布特性[J]. 煤炭学报,2013,38(7):1277-1282.
He Jingfeng,Zhao Yuemin,He Yaqun,et al. Distribution characteristic of bed density in air dense medium fluidized bed based on the Euler-Euler model[J]. Journal of Coal Science & Engineering, 2013, 38(7): 1277-1282. (in Chinese with English abstract)
[20] He Jingfeng, He Yaqun, Zhao Yuemin, et al. Numerical simulation of the pulsing air separation field based on CFD[J]. International Journal of Mining Science and Technology, 2012, 22(2): 201-207.
[21] Ansys Inc. Ansys Fluent User’s Guide[M]. Pittsburgh: AnsysInc, 2011.
[22] Gidaspow D. Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions[M].California: Academic Press Inc, 1994.
[23] Ogawa S, Umemura A, Oshima N. On the equation of fully fluidized granular materials[J]. Journal of Applied Mathematics and Physic,1980, 31(4): 483-493.
[24] Ansys Inc. Ansys Fluent Theory Guide[M]. Pittsburgh: AnsysInc, 2011.
[25] Ding J, Gidaspow D. A bubbling fluidization model using kinetic theory of granular flow[J]. Aiche Journal, 1990, 36(4): 523-538.
[26] Gidaspow D. Hydrodynamics of fluidization and heat transfer supercomputer modeling[J]. Applied Mechanics Reviews, 1986, 39(1): 1-22.
[27] Llun C K K, Savage S B, Jeffrey D J, et al. Kinetic theory of granular flow: Inelastic particles in couette flow and slightly inelastic particles in a general flow field[J]. Journal of Fluid Mechanics, 1984, 140(6): 223-256.
Numerical simulation of velocity field of sand grains in backwashing process of sand filter layer in micro-irrigation based on granular flows theory
Li Jinghai1, Liu Qingxia1, Zhai Guoliang2※, Cai Jiumao2, Zhang Wenzheng2
(1.,,455000,; 2.,,453002)
The velocity distribution of sand grains in the backwashing flow field is key to the backwashing performance of sand filter layer, such as the expansion height, distribution uniformity and the stability of fluidized state. To analyze the velocity distribution of sand grains in the backwashing process and find out the optimal backwashing speed, numerical simulation was used in this paper. Moreover, a geometric model of sand filter was established and the mesh division of the geometric model was carried out through Gambit software. Because the backwashing process of quartz sand filter layer is a solid-liquid multiphase flow system composed of water and quartz sand, we can conclude that the Eulerian model is suitable for the numerical simulation of the velocity field of sand grains by comparing the applicability of the current multiphaseflownumericalsimulationmodels such as Eulerian model, Mixture model and VOF(volume of fluid) model. At the same time, because the backwashing process of quartz sand filter layer is both a dynamic and a stable process, the transient simulation solver was adopted. Additionally, the granular flow theory was used to seal the momentum equation of the model, because of the formation of granular flows in the backwashing process. The simulation objects was the quartz sand filter layer whose thickness was 400 mm, and the equivalent grain diameter was 1.06 mm. In order to verify the reliability of simulation results, laboratory experiments of backwashing were conducted in Farmland Irrigation Research Institute, Chinese Academy of Agricultural Sciences, Xinxiang, China. The parameters such as the backwashing speed and the total height of the filter layer were measured during the experiments. And the simulation results were compared with the experimental results. Comparison results showed that the maximum simulation error of the sand grains velocity was 9.8%. So the numerical simulation results were proved to be reliable. On this basis, three cross-sections, with the height of 15, 25 and 35 cm, were selected in the filter layer and the axial velocity distribution of sand grains was analyzed. The fluidization ratio of backwashing for this simulation was 1.3, 1.5, 1.7 and 1.9 respectively. Based on the magnitude and direction of the velocity of sand grains in the three cross-sections, we can figure out whether the sand filter layer is completely fluidized or not. The stability of the fluidization state of the filter layer can be estimated by the consistency of the movement trend of sand grains in the three cross-sections and the stability of the rising zone of granular flows. The results showed that the bigger the fluidization ratio of backwashing is, the less time needed for completely fluidizing the filter layer. As a consequence, only if the fluidization ratio of backwashing is not less than 1.7, the filter layer might reach a stable state of fluidization. In a stable flow, the rising zone and the descending zone formed a stable circulation in the filter layer. As the grains swarm moved along a relatively fixed path, the ideal backwashing effect was achieved. It can be seen from the above that the optimal fluidization ratio of backwashing of the filter layer is 1.7. The research provide not only a theoretical basis and technical support for the study of the sand filter but also a reference for the determination of performance parameters for the backwashing.
models; computer simulation; irrigation; quartz sand filter layer; backwashing; multiphase flow
李景海,刘清霞,翟国亮,蔡九茂,张文正. 基于颗粒流理论的微灌砂滤层反冲洗过程砂粒速度场模拟[J]. 农业工程学报,2018,34(22):78-83. doi:10.11975/j.issn.1002-6819.2018.22.010 http://www.tcsae.org
Li Jinghai, Liu Qingxia, Zhai Guoliang, Cai Jiumao, Zhang Wenzheng. Numerical simulation of velocity field of sand grains in backwashing process of sand filter layer in micro-irrigation based on granular flows theory [J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(22): 78-83. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2018.22.010 http://www.tcsae.org
2018-05-11
2018-10-01
“十三五”国家重点研发计划(2016YFC0400202)
李景海,博士,高级工程师,主要从事微灌过滤器及水资源配置研究。Email:649923670@qq.com
翟国亮,研究员,博导,主要从事节水灌溉设备研究。 Email:275580557@qq.com
10.11975/j.issn.1002-6819.2018.22.010
S275.6
A
1002-6819(2018)-22-0078-06

