环境敏感变量优选及机器学习算法预测绿洲土壤盐分
王 飞,杨胜天,丁建丽,魏 阳,葛翔宇,梁 静
环境敏感变量优选及机器学习算法预测绿洲土壤盐分
王 飞,杨胜天,丁建丽※,魏 阳,葛翔宇,梁 静
(1. 新疆大学资源与环境科学学院智慧城市与环境建模自治区普通高校重点实验室,乌鲁木齐 830046; 2. 新疆大学绿洲生态教育部重点实验室,乌鲁木 齐 830046)
基于机器学习预测干旱区(如新疆)土壤盐分的研究目前较少涉及且敏感变量的筛选还需深入探讨。该研究比较5种机器学习算法(套索算法,The Least Absolute Shrinkage and Selection Operator-LASSO;多元自适应回归样条函数,Multiple Adaptive Regression Splines-MARS;分类与回归树,Classification and Regression Trees-CART;随机森林,Random Forest-RF;随机梯度增进算法,Stochastic Gradient Treeboost-SGT)在3个不同地理区域(奇台绿洲,渭-库绿洲和于田绿洲)的性能表现;参与的变量被分为6组:波段,植被相关变量集,土壤相关变量集,数字高程模型(digital elevation model, DEM)衍生变量集,全变量组,优选变量组(全变量组经过算法筛选后的变量集合)。通过算法筛选,以示不同研究区的盐度敏感变量。同时借助以上述6组结果评判算法的性能。结果表明:综合分析6个变量组的2和RMSE,预测精度排名如下:优选变量组>植被指数变量组>土壤相关变量组>波段>DEM衍生变量组。由于结果不稳定,全变量组未参与排名。在所有变量中,植被指数(EEVI,ENDVI,EVI2,CSRI,GDVI)和土壤盐度指数(SIT,SI2和SAIO)与土壤盐度相关性高于其他变量。综合评价以上5种算法,Lasso和MARS的预测结果出现极端异常值,但其预测结果能基本呈现土壤盐分空间分布格局。CART的结果能清晰分辨灌区和非灌区土壤盐分的分布态势,但二者内部并无太多变化且稳定性较差。RF和SGT的结果显示,二者在3个绿洲的土壤盐分值域范围和土壤盐分空间分布格局相似,纹理信息相对其他3个算法更为丰富。更为重要的是,算法在各个地区的结果都较为稳定。二者相比,SGT验证精度相对最高,其次为RF。
土壤盐分;遥感;机器学习;绿洲;Landsat OLI;数字高程模型;新疆
0 引 言
2014年,新疆的盐渍化耕地占灌溉面积约为37.72%,比2006年高出6个百分点[1],严重制约当地的经济发展和生态保护。许多学者利用地面采样数据结合环境变量探讨土壤盐渍化与地理环境之间的关系,并建立相应的土壤盐度预测模型评价其分布范围和土壤盐度严重状况[2-8]。数据挖掘被定义为通过自动化或半自动化训练并发掘大型电子数据集中存在的模式,进而基于此模式提取新数据中目标信息的过程[9]。目前,越来越多的机器学习算法被开发利用,但是基于该方法的土壤盐碱化模拟预测研究尚处于前期阶段。Taghizadeh-Mehrjardi等[10]基于分类和回归树(classification and regression trees, CART)分析环境变量与土壤盐分之间的关系并建立相应模型预测待定深度和区域的土壤盐渍化分布。该方法的优势在于不需要假定变量符合某种分布且能够处理缺失数据。在Muller和Van Niekerk的研究中[11],使用CART建立图像特征和土壤电导率之间的关系。Vermeulen和Van Niekerk将数字高程模型衍生因子作为机器学习算法(-最邻近(K-NN),支持向量机(support vector machine,SVM),CART和随机森林(random forest,RF))的输入变量,预测研究区土壤盐害影响的地区和范围[12]。结果显示,相比较而言,CART的精度最高。
纵观目前土壤属性制图研究,多半采用统计学方式,原因在于机理性模型需要的参数过多,且应用的尺度太小,推广至大尺度比较困难。土壤景观模型是结合机理模型中的关键因素,同时有能借助统计学模型将其推广至大尺度。但由于地理环境的差异性,即便是宏观上相似的干旱区,随着自然环境的变化(地貌,母质,植被和水资源等),模型的通用性会受到考验。为了能尽量准确地反演本地区的土壤盐分空间分布特征,合适的变量尤为重要。所以本研究通过选择新疆3个典型绿洲为研究靶区,检测哪些变量在干旱区识别盐分含量方面具备较高的通用性。同时,目前未有研究涉及比较不同机器学习算法在干旱区多个绿洲灌区预测盐分的性能。
综上所述,本文的研究目的主要包括以下两点。一是筛选出新疆典型绿洲(奇台绿洲,渭干河-库车河绿洲(以下简称渭-库绿洲)和于田绿洲)地区土壤盐度敏感性较高的变量。二是对比5种机器学习算法(套索算法-Least absolute shrinkage and selection operator,LASSO;多元自适应回归样条函数-Multivariate Adaptive Regression Splines, MARS;CART;RF,随机梯度增进算法-Stochastic Gradient Treeboost-SGT)的实际表现并评选出适用于绿洲土壤盐度反演的最优算法。
1 材料与方法
1.1 研究区域
奇台绿洲(89°13′~91°22′E,43°25′~49°29′N)位于新疆天山山脉东段博格达山北麓。南部为山地,中部为冲积平原,北部为戈壁沙漠区。海拔范围568~978 m。年平均降水量184.8 mm,年平均蒸发量2 141 mm,年平均气温约5.1~6.1 ℃。大部分降水发生在6-8月,年均降水量为176 mm。天然植被包括芨芨草((.)),骆驼刺(),盐爪爪((.))盐节木(()),猪毛菜()。奇台绿洲盐渍地面积11 090 hm2,占农业总面积的31%。
渭-库绿洲(80°37′~83°59′E,41°06′~42°40′N)位于塔里木盆地西北部。该范围包括新和、库车和沙雅3个县,总面积523.76×104hm2。海拔范围892~1 100 m,由西北向东南递减。该区气候异常干旱,年平均降水量51.6 mm,年平均潜在蒸散量2 356 mm,年平均气温10.5~14.4 ℃。自然条件下植被覆盖较低,优势植被群落包括芦苇()柽柳(),骆驼刺(),花花柴(),盐爪爪()等。灌区内盐碱化面积达到50%以上,其中严重盐碱化面积达30%。
于田绿洲(81°09′~82°51′E,35°14′~39°29′N)属克里雅河流域。地处塔克拉玛干沙漠南缘,昆仑山中部北坡,地势南高北低,海拔1 180~5 460 m。多年平均降水量47.1 mm,年平均气温12.4 ℃和年平均潜在蒸散量为2498 mm。绿洲土壤母质以棕漠土为主。主要的植被有胡杨()、柽柳()、芦苇()等。
1.2 遥感数据和野外采样
本研究中3个绿洲所用的卫星图像均为Landsat OLI(奇台绿洲,行列号为141/29,获取时间为2016年8月29日;渭-库绿洲,行列号为145/31,2014年9月14日,于田绿洲,行列号为145/34,获取时间为2015年9月17日)。使用ENVI 5.3 中的FLAASH模型进行大气纠正,并将数字信号转化至反射率(0~1)。纠正后的反射率数据用于计算环境变量(指数)。
采样点设计考虑了本地土壤类型,景观特征,植被类型,地貌类型和交通可达性(图1)。在野外样品采集过程中,选取样点(30 m×30 m)的土壤性质尽量相对一致,环境因素相似,异质性相对较小,每个样点用五点梅花的方式取土,随后将测试的数据进行平均作为本样点的实际观测值。奇台绿洲的采样深度为0~20 cm,样本量为101个,采样时间为2016年8月26日至9月1日。同样的采样方法应用于渭-库绿洲,样本数量189个,采样深度同样为0~20 cm,采样时间为2016年9月26日至9月1日。于田地区则选择了5种地类,代表本地不同的景观类型。分别为克里雅河岸边的农田及荒地;植被覆盖度低的沙漠;河流末端的洪水冲积平原;农田的盐碱化矮草地;绿洲内部的农田。共采集100个样本,采样深度为0~20 cm,采样时间为2015年9月13日至9月21日。将采集的土壤样品风干,研磨,并用2 mm筛网过滤。参照《土壤农业化学分析方法》[13],测定土壤中的八大离子(Ca2+,Mg2+,K+,Na+,CO32-,HCO3-,Cl-,SO42-),并用离子加和法计算土壤中的盐分含量。

图1 奇台绿洲,渭-库绿洲和于田绿洲样点分布图
1.3 环境协变量
在本研究中,基于SCORPAN公式选择用于预测土壤盐分预测的环境变量[14],涉及母质(Parent material, PM)、气候(Climate)、生物(Organism)、地形(Relief)、土壤(Soil)等多个因素。具体指数参见表1。其中地形衍生变量集源于8个空间分辨率(因研究地区地形较为平坦):30,60,90,120,150,180,210和240 m。
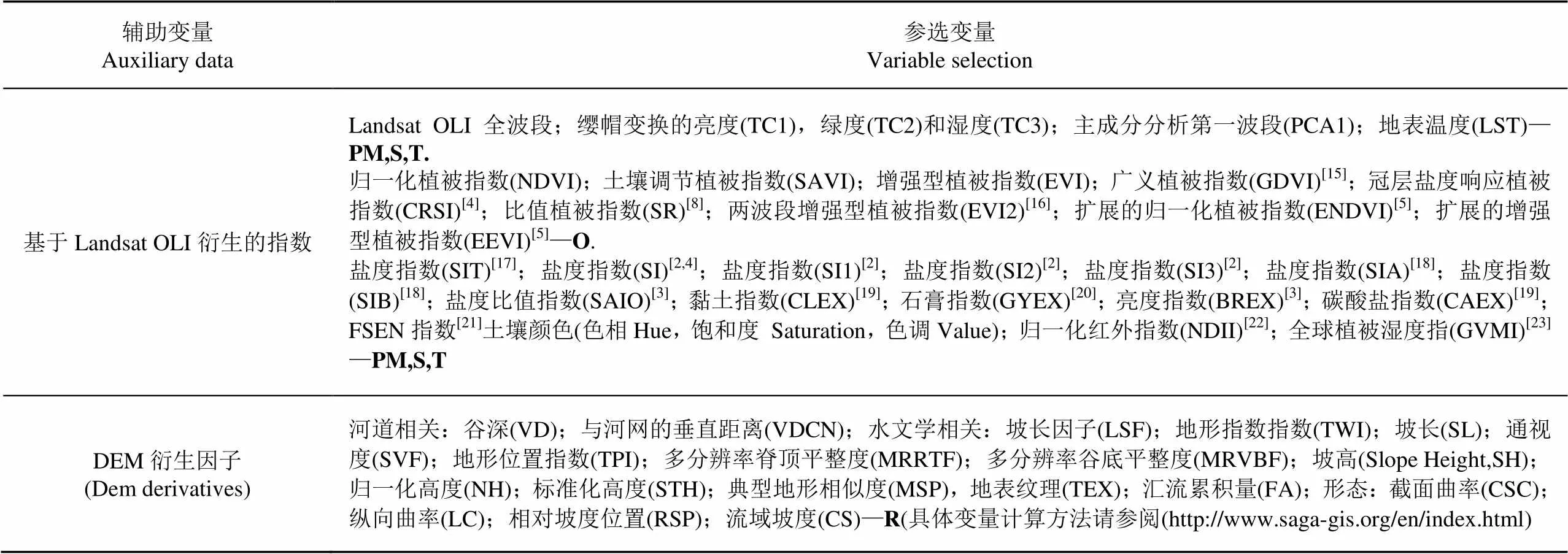
表1 基于Landsat OLI和DEM衍生的环境变量
注:PM:母质;O:生物;S:土壤;T:时间;R:地形
Note: PM: Parent material; O:Organism; S: Soil; T:Time; R:Relief
1.4 最优变量的选择
本文选择的算法都具备筛选变量的能力,但策略和方式各有不同。研究并没有限定变量个数,而是通过不同算法内在的机制进行自适应选择,以最大化算法的精度。
已有研究表明基于迭代删除潜在不相关的预测变量,有利于减少不确定性,进而提高预测精度[24-25]。本研究中,参与的变量被分为5个基本组和1个最优组:波段,植被相关变量集,土壤相关变量集,数字高程模型(digital elevation model, DEM)衍生变量集,全变量组。每个组根据迭代过程计算都会产生最优变量集合。研究之所以把变量分组在于从多个角度(各组变量数目以及变量与土壤盐之间的相关性各不同)考察算法的挖掘能力。变量优选策略源于Svetnik等[24]和Heung等[25]的研究成果:
1)首先以Landsat OLI全波段为例,将其全部输入机器学习算法。各个算法依据平均精确率减少(Mean decrease accuracy, MDA)法,将预测变量的重要性进行排序(值域范围0~100,其中100代表相对最重要,0代表最不重要)。
2)重要性排名最后一位的预测变量会被删除。剩余的变量进入下一轮排序,之后再删除最后一位变量,依次类推。直到参与的变量只剩下最后两位,循环结束。每次运算都会产生均方根误差(root mean square error,RMSE)和2。最后根据RMSE和2判断最优变量数目,原则上以RMSE最小为最优。
3)循环步骤1-2,直到遍历所有变量组,得到每个变量集的最优组合。
1.5 算法介绍及建模参数初始化设置
除MARS使用Matlab(2014)计算外,其他4种机器学习方法皆使用R语言实现,分别为Lasso的“glmnet”[26],CART的“caret”[27],RF的“randomFForest”[28]和SGT的“gbm”[29]。根据文献记载和本地试验,调整合适的初始化参数,以输出相对客观的结果。
在建模之初,为了尽量减少因缺失重要变量而出现模型偏差,通常会选择较多的自变量。然而,这可能会给建模过程带来更多的不确定性,因此需要寻找最具有强解释力的自变量集合。Lasso算法是一种集合岭回归和最小二乘法且能够实现变量集合精简的估计方法。该方法通过构造罚函数改进通用最小二乘法(OLS)技术,压缩变量系数并设定一些系数为0,同时融合岭回归核心思想保留处理共线性数据的有偏估计。因此,Lasso同时实现变量选择和回归建模[30]。在Lasso中,需要设置3个参数,分别是损失函数(此研究中设置为最小二乘法),point值设为200和steps值设置为5000。
MARS是由Friedman提出,该方法通过样条函数模拟复杂非线性关系,将其划分为若干个区域,在每个特定区域由基函数回归模型拟合。该方法是经典线性回归,样条函数和二元回归的技术组合,且可自动模拟非线性变量之间的相互作用[31]。每个区间都会产生最为合适的基本函数(Basis function)。特定范围内的基础函数是独立存在的,范围内的初始和结束点称为结(Knot)。结表示函数行为发生变化的重要结点。因此,Knot和Basis function对于在MARS中获得最佳结果具有重要作用。MARS具备以下特点:1)处理复杂的非线性变量关系时,不需要假设预测变量和预报因子的线性关系、指数关系及正态假设;2)是一种泛化能力较强的专门针对高维数据的回归方法,以“前向”和“后向”算法逐步筛选因子,具有较强的自适应性。根据Friedman的建议,Knot的初始值设为3,最大化基函数设为15。
CART采用一种二分递归分割的技术,将当前的样本集分为两个子样本集,使得生成的的每个非叶子节点都有两个分支。基本思想为:一是基于递归划分将训练样本进行分割建树,二是基于交叉验证数据进行剪枝。该方法对于输入变量分布不需要假设(即分布和独立残差),抽取规则简便且易于理解,对于异常点的容错能力好,面对存在缺失值、变量数多等问题时健壮性较高,具备一定数据噪声的抑制能力而得以广泛应用。此外,为了抑制噪声,可以通过设置节决策树深度来改进,最大深度被设置为5[27]。
随机森林是将多棵树集成的一种算法,它的基本单元是决策树。该算法的优势在于具备非线性挖掘能力;数据分布不需要符合任何假设;同时处理等级和连续变量;防止过度拟合;有效抑制数据中存在噪声;训练速度快;定量描述变量的贡献度;只需要率定少量参数。该算法仅需定义两个参数[25]:终端节点树(ntree值设置为1 000)和每个节点随机选择的变量的数量(由m定义,设定为自变量数目的1/3,平方根或者2*平方根)。后者经过重复的计算和比较,研究将其设置为2*平方根[25]。
SGT是回归树和Boosting的集成。Boosting的核心思想是:初始状态下为每个训练样本赋予一样的权重值,每次迭代训练提高错分样本的权重,降低分对样本的权重。在减少残差梯度方向上不断建立新的模型,直到误差不再降低为止。迭代次之后,得到个弱分类器,最终通过权重加和的方式集合成强分类器[32]。该算法不需要变量的先验假设,比传统的广义线性或加权模型提供更大的灵活性[32]。存在空间异质性和异常值时,SGT依然能获得较高的预测精度。该算法需要设置以下三个参数:抽样比例,树的最大化子节点个数和每次生成的树的数量。抽样比例为1时,每次迭代的样本集相同,小于1时,抽取的训练样本集都不同,有助于过拟合,这里设置为0.75[33]。树的最大化子节点个数设定6[34]。每次生成的树的数量设置为1 000。
1.6 模型验证
交叉验证对于人工智能,机器学习,模式识别,分类器等研究都具有很强的指导与验证意义。其基本思想是把原始的数据(original dataset)分成为训练集(train set)和验证集(validation set or test set)。K-fold Cross Validation(记为K-CV)是交叉验证中较为常用的方法。Taghizadeh-Mehrjardi 等[35]建议将设置为5,其优势在于计算所获结果具备无偏估计和稳定可靠的特征。同时,该验证过程需要反复的迭代而不是单次的训练-验证。该验证方法更适合规模较少的数据集。将训练数据集随机分为5个子集,其中4/5的观测值用于模型训练,1/5用于模型验证。对于文中使用的5种算法(Lasso,MARS,CART,RF和SGT),其验证过程重复10次,再求其平均值。研究使用平均方根误差(RMSE)和决定系数(2)量化最终的精度。当模型的2值趋近于1和RMSE值向零递减被认为逐步趋于最佳。
2 结果与讨论
2.1 土壤盐度分布特征
表2列出了3个绿洲野外样品土壤盐分统计特征。值域范围与前人研究结果相近[36-38],侧面验证了本研究中样本的代表性。奇台绿洲变异系数(variable coefficient, VC)说明该地表层土壤盐分含量属于中度变异性。土壤盐渍化分类标准:非盐渍土壤(<7 g/kg),低盐渍土壤(7~9 g/kg),中度盐渍土壤(9~13 g/kg),重度盐渍土(13~16 g/kg)和盐渍土(>16 g/kg))[39]。渭-库绿洲样品统计结果显示,约50%的样本属于非盐化土壤,37.57%属于极端盐碱地,VC值等于1.23,表明该绿洲土壤含盐量属于强变异性。在于田绿洲,52%的样品属于盐渍土类型,土壤盐分呈中等变异性。

表2 奇台绿洲,渭-库绿洲和于田绿洲土壤盐分统计特征
2.2 土壤盐分变化及其与环境变量的相关性
图2显示了3个绿洲土壤盐分和遥感数据衍生变量之间的相关性。由于地理环境的差异性导致土壤盐分与环境变量之间的相关性各有不同。通过初步对比得到以下结果:1)整体而言,植被指数对于3个绿洲土壤盐度空间变异的指示作用位居首列,二者呈负相关性;4组变量相关性的平均绝对值:奇台绿洲:植被指数变量组(=0.49),波段(=0.45),土壤相关指数变量组(=0.36),DEM衍生变量组(=0.08);渭-库绿洲:植被指数变量组(=0.56),波段(=0.45),土壤相关指数变量组(=0.36),DEM衍生变量组(=0.08);于田绿洲:植被指数变量组(=0.48),波段(=0.38),DEM衍生变量组(=0.18),土壤相关指数变量组(=0.16)。2)基于DEM计算的衍生指数的解释力相对薄弱,相关性显著的变量其空间分辨率都较为粗糙。3个绿洲其气候变化、土壤类型、母质、植被群落构成、农业管理方式、土地利用方式和强度各有不同,进而影响到水资源在空间上的分布方式。根据“盐随水来,盐随水走”的定律,土壤盐度的空间变异性与环境之间的响应程度表现出一定的差异性。

图2 研究区环境变量与土壤盐度之间的相关性
2.3 较为敏感的土壤盐分变异指示变量
综合对比3个绿洲发现(表3),基于Landsat OLI衍生的变量中,ENDVI,EEVI,EVI2,GDVI,CSRI,EVI2,SAIO,SIT,SI2与土壤盐分存在较为密切的关系,揭示上述指数在干旱区具备一定的通用性。植被指数ENDVI和EEVI首次应用于中国的黄河河口地区,结果表明,与土壤盐分呈显著性相关(=−0.73,=113,土壤盐分范围为0.80~35.2 g/kg)[5]。EVI2和SAIO首次用于推断干旱区土壤盐分,结果表明在干旱区该指数具备一定的盐分探测能力。在Allbed等的研究中,3个研究子区(位于沙特阿拉伯)的SIT与土壤盐分的相关性分别为=0.51,0.67和0.78[8]。本研究中SIT与土壤盐分的相关系数为0.58,在上述范围内。SI2的值为0.50(<0.01),略高于Douaoui等(=0.44,ECe>4 dS/m;=0.33,ECe>8 dS/m)[2]与Allbed等[8](=0.35,<0.01)的研究结果。GDVI(该指数的形式为(b4-b3)/(b4+b3)),当=1,等于NDVI,当=2时,对土壤盐度具有很好的预测能力(=20,=−0.87)[7],该指数在本研究中的值等于−0.63(=189)。CSRI是近年来新建的植被指数,最初应用于农业富集地区的土壤盐分评价。该指数的制定是经验性的,与任何植物生理性质无关,但与一般植物健康相关。Scudiero等[4]表明,CRSI与土壤盐度呈线性关系,2=0.56(=267,来自22个农田),高于渭-库绿洲,=−0.598(=189)。与奇台绿洲和于田绿洲相比,CSRI的表现并不突出,部分原因是由于渭-库车绿洲48%的样品(属于非盐渍化,植被覆盖度较高)来自农田,由此可见,CSRI可能更适合于植被密度较高的农田,但需要进一步验证。
DEM优选衍生变量组中筛选后的指数与本地水资源分布方式有关。观察3个研究区的结果后发现,奇台绿洲DEM衍生变量最优变量与水文有关的占多数。渭-库车绿洲以河道和地形形态衍生变量为主,于田绿洲受水文和地形形态学衍生变量双重影响。据奇台绿洲田间调查,当地多数农作物广泛采用漫灌方式(生长季节开始和收获季结束尤为常见)。次生盐渍化和水污染问题较为严重。张芳等[36]指出,奇台绿洲海拔680 m以下缓坡区为盐积区,此结果与地形衍生变量组中SH,STH和MSP的出现相一致。在渭-库绿洲,从1978年至今,为了应对人口增长和提升田间产能的需求,建成了大量的水利工程,平原水库和灌溉渠道。该地盐渍化地区的分布深受水资源再分配的影响。于田绿洲地区水文相关的地形变量占主导地位,其次是河道和地形衍生变量,这与样点的位置(大部分靠近河流)和较高的样点密度有关。因此,高分辨率的变量更敏感。

表3 基于5种机器学习筛选的奇台绿洲,渭-库绿洲和于田绿洲/的优选变量集及各指数重要性(%)
2.4 变量迭代对精度影响
图3显示了以SGT为例,变量选迭代过程和精度轨迹曲线。奇台绿洲,当变量数量等于7(2=0.49,RMSE=11.65),12(2=0.49,RMSE=11.57)和16(2=0.49,RMSE=11.59)时,预测精度相似。然而,当变量按照重要性排序从7到16连续增加时,精度不会显着提高。考虑到模型的稳定性和不确定性,使用7个变量(即=7)被认为是合适的。在渭-库绿洲,当变量的数量迭代到7和10时,这2种模型在该地的精度都比较高。因此,按照上述原则,7个变量被认为是最佳组合。于田绿洲的结果表明,当变量的数量从初始集迭代到最后2个指数时,精度最高,随着变量的增加,精度单调递减。
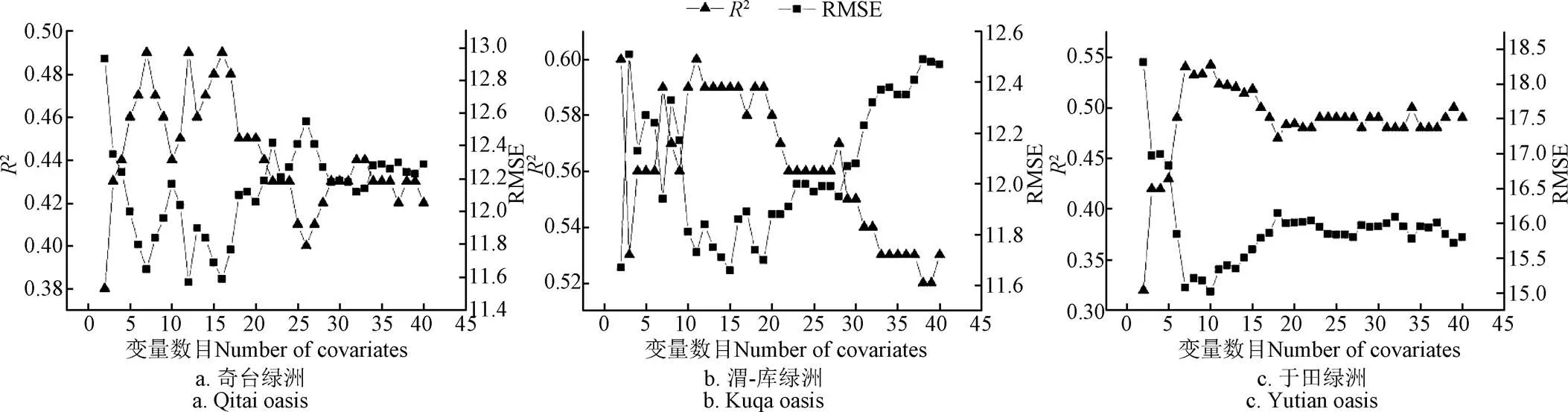
图3 研究区基于SGT的变量迭代过程和精度轨迹(重要性排名第40的变量到最后2个)
将所有变量输入算法后,与其余5个分组的结果相比,精度并没有提升,但经过变量优选后,解释力显著提高(表4)。对比5种算法,奇台绿洲的精度提升范围最大值为88%,渭-库绿洲最小值为−8.3%,最大值为35%,于田绿洲最小值为−8.3%,最大值为58%。奇台绿洲优选变量集合的最大解析力2=0.49,渭-库绿洲2=0.54,于田绿洲2=0.60。此外,研究发现优选变量组的覆盖类型(植被,地形和土壤相关变量)较为全面。以最大解释力数据集为例,奇台绿洲的前4个变量涉及植被(ENDVI),土壤(SI2)和地形(MSP 90 m);库车绿洲最优变量集涉及土壤相关(SAIO),植被(EVI2),与植被和土壤信息皆相关的B1和地形相关(VD180m)。于田绿洲最优变量组合为EEVI和EVI2,前者中的波段几乎覆盖了Landsat OLI可见光,近红外和中红外,后者对于地物背景具备一定识别性[5]。

表4 基于不同变量数据集和机器学习算法的奇台绿洲,渭-库绿洲和于田绿洲土壤盐度预测精度验证
2.5 算法挖掘效率
土壤盐分预测的准确程度主要取决于变量对土壤盐分的响应性,其次是算法的挖掘能力[4,6-7,10]。首先,观察各绿洲5组变量的结果发现,如果变量与土壤盐分之间的相关性越强,预测与实测土壤盐分之间的一致性越高。其次,机器学习算法涉及的变量个数较少时,验证精度差异不明显。当变量的数量增加后且与各土壤盐分相关性较低时,如DEM衍生变量组,较其他模型而言,SGT和RF从复杂变化环境中挖掘有用信息的能力高于其他模型。全变量组使用变量迭代优化后,各算法的精度都得以提升,其中各绿洲SGT预测精度最高且提升最为明显,3个绿洲的表现较为一致,其次是RF。LASSO是基于相对最优秀的变量建模,而MARS则考虑了非线性关系,采用分段拟合的方式,是线性和非线性的融合。SGT是不断改进一棵树,而RF则是取多棵树的平均值,从结果上看SGT的建模方式相对更适合土壤盐渍化-环境变量模型。此外,研究还针对目前机器学习中应用较广的SVM和BP神经网络与本文选择的五种方法对比,结果显示,3个绿洲中SVM和BP在5组数据对比中,2值较高,但是RMSE也较高。原因在于上述算法的学习策略中不提供变量重要性排序,无法进行迭代运算,以减少不确定性变量。
图4展示了基于5种算法预测的土壤盐度分布图。奇台绿洲南部以农田为主,整体土壤盐分含量较低。向南随着海拔高度的降低,地下水位上升,盐渍化土地以面状分布于绿洲荒漠交错带和点状分布于灌区农田分布区。研究区北部半固定沙丘地带,地下水位下降,土壤盐渍化水平相对过渡带而言有所减缓,但依然高于农田种植区。对比以上实地调查结果,基于SGT的预测结果更符合实际情况,其次是RF。CART的结果并未显示出土壤盐分的空间分布格局。LASSO的结果虽然能体现土壤盐分的分布格局,但极端异常值分布较为明显。MARS的结果显示沙漠地区和农田的土壤盐分存在趋同现象,不符合实际情况。渭-库绿洲的盐渍化土壤主要分布于灌区外围的绿洲-荒漠交错带,灌区内部亦有出现(点状)。对比5种算法,SGT和RF的预测结果更符合我们对该区盐渍化土壤分布的认知。CART的预测结果二值化现象明显,且土壤盐分含量值域区间相近的地区其内部缺少纹理信息。LASSO和MARS的预测结果中出现极端异常值,但保留相对清晰的土壤盐度分布格局信息。于田绿洲,盐渍化土壤主要出现于灌区外围的裸地以及河流两侧。5种算法的预测结果从格局分布上而言,都符合该调查事实,但SGT和RF的结果更接近实地情况。剩余3种算法都有负值出现。综上所述,结合2和RMSE的结果,研究认为SGT的预测结果更符合实际情况,是干旱区土壤盐分的首选算法,其次为RF。

图4 基于LASSO, MARS, CART, RF和SGT预测的奇台,渭-库和于田绿洲土壤盐度空间分布
为了对比本文研究结果与已有成果,本文检索近些年使用Landsat数据模拟和验证土壤盐分相关研究,并总结如下:研究区包括伊拉克中部地区,美国加利福尼亚州西部的圣华金河谷,中国北方内蒙古河套灌区,黄河三角洲,阿尔及利亚,土耳其,新疆北部的玛纳斯绿洲,新疆南部的渭-库绿洲等。采样深度包括0~30 ,0~20,0~10 cm。2值等于0.874,0.483,0.78,0.45,0.65,0.93,0.92,0.44。研究方法包括线性和非线性模型。关键变量或者指数包括GDVI,EEVI,SI,NDVI,CRSI,SAVI等。回顾上述研究,由于取样深度,敏感变量,研究法方法,验证方法和研究区域的地理环境的差异,可以看出结果是多样的。此外,基于机器学习的土壤盐分预测在新疆3个研究区涉及较少。所以本文的研究结果是对机器学习对该领域的知识实践和内容补充。
3 结 论
1)总体而言,根据2和RMSE,5个变量组的预测精度排名如下:优选变量组>植被指数变量组>土壤相关变量组>波段>DEM衍生变量组。
2)研究发现以下变量对于本地盐度变化具有较强的指引性和普适性:EEVI,ENDVI,EVI2,CSRI,GDVI,SIT,SI2,SAIO。
3)综合对比3个绿洲的测试结果,基于回归树结构的机器学习(随机梯度增进算法SGT和随机森林RF)总体性能优于分类与回归树CART,多元自适应回归样条函数MARS和套索算法LASSO。其中,SGT的预测精度相对最高(2=49,RMSE=11.65;2=0.54,RMSE=15.08;2=0.60,RMSE=11.67)。其次为RF(2=0.48,RMSE=12.02;2=0.46,RMSE=16.79;2=0.60,RMSE=12.38)。基于土壤盐渍化发生机理的复杂性,以及其与变量之间的非线性关系,更多呈现出的是弱关联。如何将弱关系组合成鲁棒性更好的模型正是RF和SGT的强项,而MARS和Lasso在这一方面稍显不足。
[1] 田长彦,买文选,赵振勇. 新疆干旱区盐碱地生态治理关键技术研究[J]. 生态学报,2016,36(22):7064-7068.
Tian Changyan, Mai Wenxuan, Zhao Zhenyong. Study on key technologies of ecological management of saline alkali land in arid area of Xinjiang[J]. Acta Ecologica Sinica, 2016, 36(22): 7064-7068. (in Chinese with English abstract)
[2] Douaoui AEK, Nicolas H, Walter C . Detecting salinity hazards within a semiarid context by means of combining soil and remote-sensing data[J]. Geoderma, 2006, 134(1): 217-230.
[3] Metternicht GI, Zinck JA. Remote sensing of soil salinity: Potentials and constraints[J]. Remote Sensing of Environment, 2003, 85(1): 1-20.
[4] Scudiero E, Skaggs T H, Corwin DL. Regional-scale soil salinity assessment using Landsat ETM+canopy reflectance[J]. Remote Sensing of Environment, 2015, 169: 335-343.
[5] 陈红艳,赵庚星,陈敬春,等. 基于改进植被指数的黄河口区盐渍土盐分遥感反演[J]. 农业工程学报,2015,31(5):107-114.
Chen Hongyan, Zhao Gengxing, Chen Jingchun, et al. Remote sensing inversion of saline soil salinity based on modifiedvegetation index in estuary area of Yellow River[J]. Transactions of the Chinese Society of Agricultural Engineering(Transactions of the CSAE), 2015, 31(5): 107-114. (in Chinese with English abstract)
[6] Scudiero E, Skaggs TH, Corwin DL. Regional scale soil salinity evaluation using Landsat 7, western San Joaquin Valley, California, USA[J]. Geoderma Regional, 2014(2/3): 82-90.
[7] Wu W, Mhaimeed AS, Al-Shafie WM, et al. Mapping soil salinity changes using remote sensing in Central Iraq[J]. Geoderma Regional, 2014, 2-3: 21-31.
[8] Allbed A, Kumar L, Aldakheel YY. Assessing soil salinity using soil salinity and vegetation indices derived from IKONOS high-spatial resolution imageries: Applications in a date palm dominated region[J]. Geoderma, 2014, 230-231: 1-8.
[9] Witten IH, Frank E, Hall MA. Data Mining: Practical Machine Learning Tools and Techniques, Second Edition (Morgan Kaufmann Series in Data Management Systems)[M]. San Francisco: Morgan Kaufmann Publishers Inc. 2011: 206-207.
[10] Taghizadeh-Mehrjardi R, Minasny B, Sarmadian F, et al. Digital mapping of soil salinity in Ardakan region, central Iran[J]. Geoderma, 2014, 213: 15-28.
[11] Muller SJ, Van Niekerk A. Identification of WorldView-2 spectral and spatial factors in detecting salt accumulation in cultivated fields[J]. Geoderma, 2016, 273: 1-11.
[12] Vermeulen D, Van Niekerk A. Machine learning performance for predicting soil salinity using different combinations of geomorphometric covariates[J]. Geoderma, 2017, 299: 1-12.
[13] 鲁如坤. 土壤农业化学分析方法[M]. 北京:中国农业科技出版社,1999.
[14] Mcbratney A B, Santos M L M, Minasny B. On digital soil mapping[J]. Geoderma, 2003, 117(1): 3-52.
[15] Wu W. The generalized difference vegetation index (GDVI) for dryland characterization[J]. Remote Sensing, 2014, 6(2): 1211-1233.
[16] Mondal P. Quantifying surface gradients with a 2-band Enhanced Vegetation Index (EVI2)[J]. Ecological Indicators, 2011, 11(3): 918-924.
[17] Tripathi NK, Brijesh KR. Spatial modelling of soil alkalinity in GIS environment using IRS data[C]. Kualalampur: Paper presented at the 18th Asian Conference in Remote Sensing, 1997.
[18] Abbas A, KhanS. Using remote sensing techniques for appraisal of irrigated soil salinity[C]. New Zealand: MODSIM 2007 International Congress on Modelling and Simulation, 2007.
[19] Boettinger J L, Ramsey R D, Bodily J M. Digital Soil Mapping with Limited Data [M].Dordrecht: Springer, 2008: 193-202.
[20] Nield SJ, Boettnger JL, Ramsey RD. Digital mapping gypsic and nitric soil areasvusing Landsat ETM data[J]. Soil Science Society of America Journal, 2007(71): 245-252.
[21] Yu R, Liu T, Xu Y, et al. Analysis of salinization dynamics by remote sensing in Hetao Irrigation District of North China[J]. Agricultural Water Management, 2010, 97(12): 1952-1960.
[22] Hardisky M S, Klemas V, Smart MR. The influence of soil salinity, growth form, and leaf moisture on the spectral radiance of Spartina Alterniflora canopies[J]. Photogrammetric Engineering and Remote Sensing, 1983, 48(1): 77-84.
[23] Ceccato P, Gobron N, FlasseS, et al. Designing a spectral index to estimate vegetation water content from remote sensing data: Part 1[J]. Remote Sensing of Environment, 2002, 82(2): 188-197.
[24] Svetnik V, Liaw A, Tong C, et al. Random forest: A classification and regression tool for compound classification and QSAR modeling[J]. Journal of Chemical Information and Computer Sciences , 2003, 43(6): 1947-1958.
[25] Heung B, Bulmer CE, Schmidt MG. Predictive soil parent material mapping at a regional-scale: A Random Forest approach[J]. Geoderma, 2014, 214: 141-154.
[26] Friedman J, Hastie T, Tibshirani R. Regularization paths for generalized linear models via coordinate descent[J]. Journal of Statistical Software, 2010, 33(1): 1-22.
[27] Kuhn M, Leeuw JD., Zeileis A. Building predictive models inusing the caret package[J]. Journal of Statistical Software, 2008, 28(5): 1-26.
[28] Liaw A, Wiener M. Classification and Regression by randomForest. R News, 2002, 2: 18-22.
[29] Ridgeway G. gbm: generalized boosted regression models R package version 2.1.1, 2015. https://CRAN.R-project.org/package=gbm.
[30] Robert T. Regression Shrinkage and Selection via the Lasso[J]. Journal of the Royal Statistical Society: Series B Statistical Methodology, 2011, 73(3):273-282.
[31] Friedman JH. Multivariate Adaptive Regression Splines[J]. The Annals of Statistics, 1991, 19(1):1-67.
[32] Friedman JH. Stochastic gradient boosting[J]. Computational Statistics & Data Analysis, 2002, 38(4): 367-378.
[33] Angileri SE, Conoscenti C, Hochschild V, et al. Water erosion susceptibility mapping by applying Stochastic Gradient Treeboost to the Imera Meridionale River Basin (Sicily, Italy)[J]. Geomorphology, 2016, 262: 61-76.
[34] Schillaci C, Lombardo L, Saia S, et al. Modelling the topsoil carbon stock of agricultural lands with the stochastic gradient treeboost in a semi-arid Mediterranean region[J]. Geoderma, 2017, 286: 35-45.
[35] Taghizadeh-Mehrjardi R, Nabiollahi K, Kerry R. Digital mapping of soil organic carbon at multiple depths using different data mining techniques in Baneh region, Iran[J]. Geoderma, 2016, 266: 98-110.
[36] 张芳,熊黑钢,田源,等. 区域尺度地形因素对奇台绿洲土壤盐渍化空间分布的影响[J]. 环境科学研究,2011,24(7):731-739.
Zhang Fang, Xiong Heigang, Tian Yuan, et al. Impacts of regional topographic factors on spatial distribution of soil salinization in Qitai oasis[J]. Research of Environmental Sciences, 2011, 24(7): 731-739. (in Chinese with English abstract)
[37] Gong L, Ran Q, He G, et al. A soil quality assessment under different land use types in Keriya river basin, Southern Xinjiang, China[J]. Soil & Tillage Research, 2015(146): 223-229.
[38] 张飞,塔西甫拉提·特依拜,丁建丽. 渭干河-库车河三角洲绿洲土壤盐渍化现状特征及其与光谱的关系[J]. 环境科学研究,2009,22(2):227-235.
Zhang Fei, Tashpolat Tiyip, Ding Jianli. Relationships between soil salinization and spectra in the delta oasis of Weigan and Kuqa Rivers[J]. Research of Environmental Sciences, 2009, 22(2): 227-235. (in Chinese with English abstract)
[39] 新疆维吾尔自治区土壤普查办公室. 新疆土壤[M]. 北京:科学出版社,1996:52.
Environmental sensitive variable optimization and machine learning algorithm using in soil salt prediction at oasis
Wang Fei, Yang Shengtian, Ding Jianli※, Wei Yang, Ge Xiangyu, Liang Jing
(1.,,,830046,; 2.,/,830046,)
The salt-affected cultivated land in Xinjiang accounts for about 37.72% of the irrigated area, which seriously restricts local economic development and ecological stability. In order to evaluate the distribution and severity of soil salinization, many scholars establish a corresponding soil salinity prediction model based on ground sampling data and environmental variables. The research on predicting soil salinity in arid areas (such as Xinjiang) based on machine learning is less involved. And the screening of sensitive variables needs to be further explored. Sensitive variables contribute to reduce the uncertainty of machine learning algorithms, and thus improve the prediction accuracy. The study aims to compare 1) Performance of five machine learning algorithms (The Least Absolute Shrinkage and Selection Operator-LASSO; multivariate adaptive regression spline function, Multiple Adaptive Regression Splines-MARS; Classification and Regression Tree, Classification and Regression Trees-CART; Random Forest, Random Forest-RF; Stochastic Gradient Treeboost-SGT) in three different geographic regions (Qitai oasis, Kuqa oasis and Yutian oasis); 2) The variables involved are divided into five groups: bands, vegetation-related variable dataset, soil-related variable dataset, digital elevation model (DEM) derived variable dataset, full variable group, optimized variables group(screening in full variable group by algorithm to show salinity-sensitive variables in different study areas). Then, the performance of the algorithm is judged by the results of each dataset. According to2and RMSE, the prediction accuracy of the five variable groups is ranked as follows: optimized variable group > vegetation index variable group > soil related variable group > bands > DEM derived variable group. Among all variables, vegetation index (EEVI, ENDVI, EVI2, CSRI, GDVI) and soil salinity index (SIT, SI2 and SAIO) are more correlated with soil salinity than other variables. When the number of variables involved is scarce, the difference in verification accuracy of each algorithm is not obvious. When the number of variables increases and the correlation with soil salinity is low, such as the DEM derived variable group, SGT and RF have higher ability to mine useful information from complex environments than other algorithms. Based on the algorithm selected, the prediction results of Lasso and MARS have extreme abnormal values, although they basically show the distribution of soil salinity. The results of CART showed that the distribution of soil salinity in irrigation and non-irrigation areas can be clearly distinguished, but there is not much change inside. The results of RF and SGT show that soil salinity range and spatial distribution of soil salinity in the three oases are similar, and the texture information is more abundant than the other three algorithms. More importantly, the results of this these 2 algorithms in each region are relatively stable. Among 5 algorithms, SGT verification accuracy is highest,followed by RF.
soil salt; remote senseing; machine learning; oasis; landsat OLI; digital elevation model; Xinjiang
王 飞,杨胜天,丁建丽,魏 阳,葛翔宇,梁 静. 环境敏感变量优选及机器学习算法预测绿洲土壤盐分[J]. 农业工程学报,2018,34(22):102-110.doi:10.11975/j.issn.1002-6819.2018.22.013 http://www.tcsae.org
Wang Fei, Yang Shengtian, Ding Jianli, Wei Yang, Ge Xiangyu, Liang Jing. Environmental sensitive variable optimization and machine learning algorithm using in soil salt prediction at oasis[J]. Transactions of the Chinese Society of Agricultural Engineering (Transactions of the CSAE), 2018, 34(22): 102-110. (in Chinese with English abstract) doi:10.11975/j.issn.1002-6819.2018.22.013 http://www.tcsae.org
2018-04-10
2018-09-12
国家自然科学基金联合基金项目(U1603241),国家自然科学基金(41661046)、自治区科技支疆项目(201591101)、新疆大学博士启动基金(BS150248)、新疆维吾尔自治区重点实验室专项基金(2014KL005)、国家自然科学基金(新疆联合基金本地优秀青年人才培养专项(U1503302))
王 飞,博士,主要从事遥感应用研究。Email:volitation610@163.com
丁建丽,博士,教授,主要从事干旱区环境演变与遥感应用研究,Email:watarid@xju.edu.cn
10.11975/j.issn.1002-6819.2018.22.013
S153
A
1002-6819(2018)-22-0102-09

