基于扩展的低阶多元广义线性模型的脑节点识别方法

杨雅倩，唐绍婷

(1.数学、信息与行为教育部重点实验室(北京航空航天大学)，北京 100191；2.北京航空航天大学 大数据科学与脑机智能高精尖创新中心，北京 100191；3.北京航空航天大学 数学与系统科学学院，北京 100191)(*通信作者电子邮箱tangshaoting@buaa.edu.cn)

0 引言

功能性磁共振成像(functional Magnetic Resonance Imaging, fMRI)技术是一种通过检测血管中血氧水平变化来测量大脑活动的技术，它因其无创性和高空间分辨率而被广泛运用于大脑活动的研究当中，现已有多篇相关文章，其中一个重要研究方向是比较不同条件下的大脑反应。具体而言，在许多心理fMRI实验中，研究人员对两次实验中的大脑反应进行比较，旨在找出不同环境下对某一刺激具有不同反应的大脑区域。

一种常见的fMRI实验数据分析方法是广义线性模型(General Linear Model, GLM)[1]，它通过血液动力学响应函数(Hemodynamic Response Function, HRF)反映不同大脑节点对不同类型刺激的响应情况。在此基础上又发展了参数模型、非参模型、半参模型等多种HRF估测方法，其中参数方法主要利用有限模型参数来刻画不同HRF之间的差异特征，具体包括泊松模型[2]和经典血液动力学响应函数模型(Canonical HRF, Canonical)[3]等；非参数方法通常将HRF表示为一系列基函数线性组合的形式，因此在衡量不同大脑区域HRF函数特征时更加灵活，其主要包括平滑有限脉冲响应(Smooth Finite Impulse Response, SFIR)[4]和正则化和广义交叉验证(Tikhonov-regularization and Generalized-Cross-Validation, Tik-GCV)[5]；此外，基于大脑活动的群体一般性和个体特异性，Zhang等[6-7]建立了更为灵活的半参数模型。

上述基于GLM框架的HRF计算模型都是单节点方法，即一次只对一个大脑节点的fMRI时间序列进行分析。由于空间上相邻的节点往往具有相似的fMRI数据，因此将大脑的空间信息并入HRF计算中将提升模型效果。基于同一区块大脑节点享有共同的函数形状而仅仅在振幅上有所不同这一假设，Vincent等[8]在大脑区块贝叶斯模型[9-10]的基础上提出HRF振幅空间先验；Chaari等[11]进一步提出了同一大脑区块中随空间变化的HRF振幅先验，并开发了联合分割检测估计程序。同时，fMRI研究向多个体、多维度数据发展，例如Degras等[12]提出了多个体功能磁共振成像HRF估计的贝叶斯模型，Zhang等[13-14]建立了适用于fMRI时间序列中复杂时间空间相关性的贝叶斯方法。

现有的基于GLM框架的模型在进行大脑反应比较实验时，通常需要提取HRF的某些低维特征(如高度等)，利用假设检验对这些低维特征进行比较，进而获取两次实验中反应不同的大脑节点。然而这种方法只能比较HRF某一特征(如高度)的差异而忽略了其他特征(如函数形状)的差异，导致估测结果具有很大的不确定性。而假设检验本质上是对每一个节点进行分析，因此忽略了fMRI数据的空间特性，导致被识别节点的准确度较低。针对这一缺陷，Zhang等[15]提出了综合所有脑节点空间信息的低阶多元广义线性模型(Low-Rank Multivariate General Linear Model, LRMGLM)，该模型利用空间矩阵灵活描述了HRF的变化，识别节点准确率更高，但fMRI数据的低信噪比和高变异性导致其计算复杂、计算效率低下。此外，由于LRMGLM只能对同一实验的大脑反应进行比较，因此在比较不同实验的大脑反应时，需要额外设置一组相同的刺激作为参考项，适用范围有限。

对此，本文提出一种基于扩展的LRMGLM(Extended LRMGLM, ELRMGLM)的脑节点识别方法。该方法建立了可同时处理两次实验所有节点数据的ELRMGLM模型，该模型通过将血液动力学响应函数(HRF)的特征矩阵转化为两个低阶矩阵相乘的形式，在实现脑节点灵活比较的同时简化参数运算。模型参数利用基于fMRI数据时空特性的优化函数和迭代算法进行估测，同时为降低模型对fMRI数据高变异性和低信噪比的敏感度，开发了基于K-means的快速选择策略来实现两次实验中反应不同大脑区域的快速选择。

1 本文模型建立

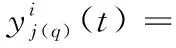
(1)

其中:

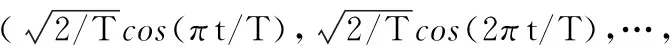
以往基于GLM框架的方法一次只对一个大脑节点或一次实验数据进行单独处理，本文提出一个可以同时处理两次实验所有节点数据的联合模型，以更多的时空信息来减少fMRI数据中噪声的干扰。由于不同个体大脑节点的HRF形状不同，首先利用B-样条插值对其进行拟合：

(2)

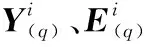
(3)

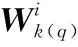
(4)

相较于LRMGLM，ELRMGLM可以直接处理两次实验所有节点的数据信息，不仅比原模型适用范围更广，而且可以利用更多的时间空间信息来提高识别的准确度。相较于传统的单节点模型，ELRMGLM可以通过保持相应Uk(q)不变，对Vk(q)进行比较的方法来实现对HRF灵活而全面的比较。例如，在计算过程中可以令U2(1)=U2(2)，比较V2(1)和V2(2)的估计值来识别两次实验中对第二种刺激有不同反应的大脑区域。

2 参数估计

2.1 优化函数

在利用上述模型对数据进行分析时，通常希望估计得到的Y值尽可能地接近真实值，令

q=1,2}

则有如下代价函数：

SSE(Θ)=

由于HRF在时间上连续，为避免过度拟合，得到矩阵Uk(q)上的时间平滑惩罚项：

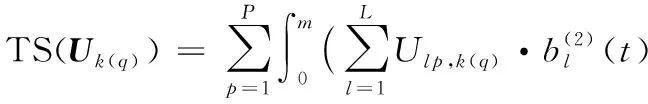
(5)

同时由于空间上相邻的大脑节点通常有相似的fMRI时间序列和HRF函数，因此得到矩阵Vk(q)上的空间平滑惩罚项：

(6)

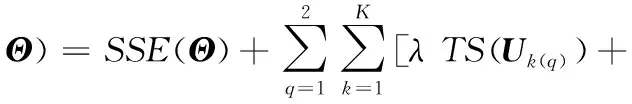
τPS(Vk(q))]

(7)

2.2 迭代算法

1)给定V，找到U、β，最小化

2)给定U、β，找到V，最小化

上述迭代算法的计算效率主要取决于两个最优子问题的计算效率，由于步骤1)、2)中的目标函数均为二次函数且存在最优解析表达式，因此可对其进行直接求解，具体推导过程在此不多作赘述。当数据量较大、数据维度过高时，直接求解可能耗时较长，此时可利用最速梯度下降法加速运算。

3 基于K-means的快速选择策略

惩罚参数λ和τ分别控制着HRF的时间平滑性和空间平滑性。在惩罚优化问题中，普通交叉验证(Ordinary Cross Validation, OCV)和广义交叉验证(Generalized Cross Validation, GCV)[18]是选择惩罚参数的经典方法；在成像数据分析中，文献[19-20]提出了基于GCV的选择过程，同时文献[21]对约束最大似然法(Restricted Maximum Likelihood, REML)进行了研究。由于本文节点数量较多且有两个惩罚参数，OCV耗时过长而REML不能直接适用，因此提出了基于K-means的快速选择策略。

由于本文的研究重点是比较两次实验中反应不同的大脑节点而非计算HRF的具体值，即只需要选择能清楚区分反应相同和反应不同脑节点的惩罚参数组合，因此可利用聚类方法加快惩罚参数和大脑节点的选择过程，将轮廓系数作为选择标准，在提高模型对惩罚参数容忍度的同时保证所选节点的准确性，具体过程如下：

1)对每个惩罚参数，在e-1～e5范围内选取大量候选参数值，利用2.2节中提到的迭代算法对带有不同惩罚参数组合的ELRMGLM进行模型参数估计，得到相应的时间矩阵Uk(q)和空间矩阵Vk(q)。

2)计算每组惩罚参数对应矩阵Vk(q)在两次实验中的差值S=|Vk(1)-Vk(2)|，其中k为所要比较的刺激类型。

3)对每组惩罚参数，利用K-means聚类将所有节点的S值分为两类，选择轮廓系数最大的惩罚参数组合和聚类结果，其中S均值较大的群组为两次实验中对刺激k反应不同的大脑节点集合。

上述快速选择策略的原理在于两方面：首先，大部分惩罚参数组合对应的大脑节点S值可以被自然地分为两部分，一部分在一个较小值附近上下浮动，另一部分的S值则显著较大，它们分别代表了由生理噪声引起的低频漂移和两次实验中不同的大脑反应，因此可通过聚类方法加以区分；其次，不同的惩罚参数组合影响了两组节点S值的差异性以及各组节点S值的稳定性，从而影响了聚类结果的准确性，而轮廓系数是一种评价聚类效果好坏的方式，它衡量了个体相较其他群集与其所属群集的相似程度，其范围从-1到1，轮廓系数值越大表明聚类效果越好，因此可将轮廓系数作为惩罚参数的选择标准。一组轮廓系数较高的惩罚参数组合会使大脑节点的S值具有高差异性和高稳定性，聚类效果较好，从而保证了被选节点的准确性和可靠性。

聚类方法提高了算法对不同惩罚参数组合的容忍度，高轮廓系数保证了所选节点的准确性，通过采用基于K-means的快速选择策略，利用聚类加快惩罚参数和大脑节点的选择过程，可以在保证准确性的同时快速找到两次实验中反应不同的大脑区域。

4 实验分析

4.1 实验数据

本文采用与文献[22-24]中真实fMRI实验相同的实验设计进行分析，该实验使用了以频率27.9%、21.1%、50.8%和0.2%随机出现的4种不同刺激，共有106个受试者，每个受试者的fMRI时间序列包含205次扫描，每次扫描时间为2 s。考虑到LRMGLM只适用于存在参考项的实验数据，本文采用文献[15]中使用的实验数据集。该数据集共含有三组fMRI数据，分布在15×15×15的大脑网格上。在组1中，HRF函数服从经典形式且前两种刺激的HRF在振幅和延迟上均不同；在组2中，HRF函数形状改变，其余与组1保持相同；在组3中，改变第二种刺激的振幅使得前两种刺激的HRF仅仅在延迟时间上有所不同，其余与组2保持相同。此外，该数据集中与第二种刺激有关的HRF参数只针对中心9×9×9的节点网格，其余大脑节点的HRF参数与第一种刺激相同。为比较实际问题中大脑节点在两次实验的中不同反应，本文增设含三组相同fMRI数据的实验二，并令其中与第二种刺激有关的HRF参数只针对中心偏右的5×9×9大脑网格，其余与实验一保持相同。此时约9.6%的大脑节点在两次实验中对第二个刺激反应不同。

值得注意的是，本文采用的实验设置并不完全遵循提出的ELRMGLM，尽管如此，实验结果将表明ELRMGLM方法能够超越更适合该实验数据的单节点分析方法和LRMGLM。

4.2 实验结果与分析

本文将提出的ELRMGLM运用于实验数据，为保持运算简洁，令P=2来刻画不同个体大脑节点HRF在振幅和延迟上的差异。图1展示了两次实验中对第二种刺激反应不同的大脑区域，其中深色区域表示被选中节点，白色区域表示未选节点，X、Y、Z分别表示大脑节点的三维坐标。可以看到，ELRMGLM方法选中了大脑中心偏左的4×9×9网格，准确度较高。

图1 被选中节点图像Fig. 1 Image of selected voxels

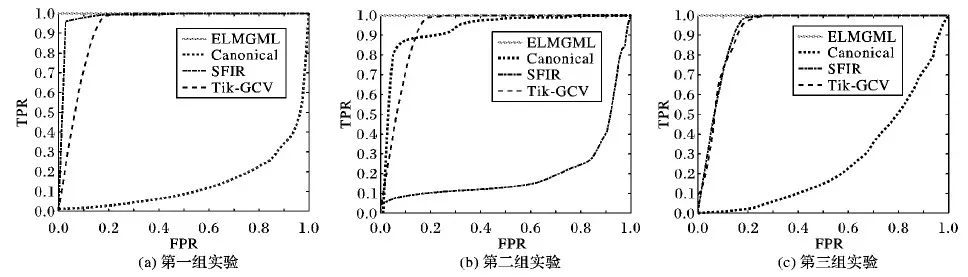
图2 三组实验数据的ROC曲线Fig. 2 ROC curves of three experimental datasets

下面将ELRMGLM分别与canonical方法[3]、SFIR方法[4]和Tik-GCV方法[5]进行比较。在进行计算时，先用上述单节点方法对HRF进行估计，再提取得到的HRF低维特征(如高度)，通过t假设检验对提取的低维特征进行比较，进而获得两次实验中反应不同的大脑区域。通过改变t检验中的P值，得到了显示不同临界值对应的真正类率(True Positive Rate, TPR)和负正类率(False Positive Rate, FPR)组合的受试者工作特征曲线(Receiver Operator characteristic Curve, ROC)。为进行比较，本文还通过使用不同的惩罚参数组合画出了ELRMGLM的ROC曲线，具体如图2所示。

从图2可知：Canonical方法在第一组和第三组实验数据中表现较差，但在第二组实验数据中表现较好，其TPR和FPR分别达到了约80%和4%。与之相反，SFIR在第一组和第三组数据中表现较好，其TPR和FPR分别达到了约95%、3%和99%、20%，但在第二组数据中表现一般。Tik-GCV在所有单节点分析方法中表现最为稳定，其TPR和FPR在三组数据中均达到99%和20%左右。通过使用第3章基于K-means的快速选择策略，本文提出的ELRMGLM在三组实验数据中均表现优异，其TPR和FPR均实现了99%以上和1%以下 (其TPR和FPR分别达到99.73%、0.44%，99.99%、0.09%和99.99%、0.01%)，比以上三种方法的最优结果分别提升了约20%、8%、20%，不仅实现了高敏感度(sensitivity)和高特异度(specificity)，同时在不同的数据集上表现稳定。

下面以第一种刺激作为参考项，对ELRMGLM和LRMGLM方法进行比较，其结果如表1所示。可以看到在三组实验中，ELRMGLM对两次实验中反应不同的大脑节点识别准确度略高于LRMGLM。在计算时间上，ELRMGLM的平均迭代次数少于100而LRMGLM需要迭代上万次；同时ELRMGLM的单次迭代时间为8 s，远小于LRMGLM的单次迭代时间60 s。不难算出，ELRMGLM的计算时间是LRMGLM的1/750，算法效率大幅提高。

表1 ELRMGLM与LRGMLM方法比较Tab. 1 Comparison of ELRMGLM and LRGMLM

5 结语

本文提出了一种用于识别两次实验中反应不同大脑区域的扩展的低阶多元广义线性模型(ELRMGLM)。该模型同时综合了两次实验的数据信息，通过带惩罚项的优化函数考虑了fMRI数据的时空特性，并利用K-means聚类提高了模型对参数的容忍度，进而实现了对大脑节点的快速准确识别。通过在三组实验数据集上的分析，该模型在准确度、计算效率和稳定性方面均高于现有模型。ELRMGLM主要用于群体大脑活动的评估，对个体大脑反应的比较还稍有欠缺，因此如何扩展ELRMGLM使其适用于大脑活动的个体差异将成为下一步的研究重点。