空间调制系统下改进的QRD-M检测算法

周 围,郭梦雨,2,向丹蕾,2

(1.移动通信技术重庆市重点实验室(重庆邮电大学),重庆 400065; 2.重庆邮电大学 通信与信息工程学院,重庆 400065)(*通信作者电子邮箱1342373012@qq.com)

0 引言

作为无线移动通信领域的重大突破,多输入多输出(Multiple Input Multiple Output, MIMO)天线技术分别在收发两端配置多根天线,在不增加系统带宽和发射功率的情况下,多倍地提高频谱利用率和系统信道容量,同时也可以提高信道的可靠性[1]。但是随着天线数量的增多存在需要额外的计算量来提供天线间同步(Inter-Antenna Synchronization, IAS)信息、相同的时频资源内同时并行传输数据会产生信道间干扰(Inter-Channel Interference, ICI)、多个射频(Radio Frequency, RF)链路带来的高昂的设计成本等问题[2]。

对于以上问题,在2006年,Mesleh等[3]提出了一种名为空间调制(Spatial Modulation, SM)技术的新型多天线传输方案。该技术仍然基于MIMO系统,但不同的是SM技术在每一发送时隙只激活一根天线用来发送数据,它利用激活天线位置对应的索引值来映射一部分输入信息比特,扩展了空间维度,构成了新型三维星座调制图，因此可以有效避免天线间同步和信道间干扰的问题；又因为SM 技术的单射频特性,所以还可以有效地降低RF链路的成本开销。SM技术的这些优势,使其受到业界研究人员的高度关注。

与传统MIMO技术的解调不同,在SM系统中解调器不仅需要检测发送符号,还需要检测天线序号。其中最大似然(Maximum Likelihood, ML)检测算法虽然可以获得最佳的误码率,但由于遍历搜索所有的激活天线索引和调制符号，因此会导致非常高的计算复杂度,很难应用到实际工程中[4]，因此一些复杂度较低的次优检测算法被人们相继提出,如最大比合并(Maximum Ratio Combining, MRC)检测算法[5]、迫零(Zero-Forcing,ZF)检测算法、最小均方误差(Minimum Mean Squared Error,MMSE)检测算法[6]、球形译码(Sphere Decoding, SD)检测算法[7]和匹配滤波(Matched Filters, MF)检测算法[8]等。在文献[9]中则提出将M算法运用到SM系统的检测当中。

为了降低计算复杂度,文献[10]在MIMO系统中提出了基于QR分解的M算法(M-algorithm based on QR decomposition, QRD-M),该算法在进行检测前先对信道矩阵进行QR分解(QR-decomposition),然后将信号检测变为一个树形结构搜索。基于上述思想,为降低计算复杂度,本文将QRD-M检测算法运用到SM系统中。传统的MIMO系统中,QRD-M检测算法只需检测发送符号,而在SM系统中不仅需要检测发送符号,还需要检测天线的索引,最小分支度量会受到发射端天线数和调制阶数两方面影响。针对上述问题,对树形搜索的结构作相应的调整,本文提出一种适用于SM系统的QRD-M信号检测算法。由于传统的QRD-M检测算法中每层固定的保留M个节点,会造成计算量的增加，因此通过对累积分支度量设计阈值提出一种具有动态M值的低复杂度的动态M值QRD-M检测算法,即LC-QRD-dM(Low-Complexity QR-Decomposition M-algorithm with dynamic value ofM)算法,减小计算复杂度。同时为了使改进算法在信道深度衰落时具有相对较好的检测性能,则对LC-QRD-dM算法在低信噪比(Signal to Noise Ratio, SNR)时,对保留节点的判断条件作出了相应的调整, 进一步提出一种基于信道状态的动态M值QRD-M检测算法,即CS-QRD-dM(QR-Decomposition M-algorithm with dynamic value ofMbased on Channel State)，改善检测性能。

1 系统模型

图1为一般的空间调制系统模型。与传统的调制方式不同,在空间调制系统中,每发送时隙激活一根发射天线,同时该激活天线也用于传输符号。假设发送端天线数与接收端天线数分别为Nt、Nr,数字调制方式为L阶的正交幅度调制(L-order Quadrature Amplitude Modulation, L-QAM)。如图1所示比特流b分成两个部分：一部分用于确定激活天线索引,另一部分用于传统的星座点调制。其中lb (L)位比特由调制符号携带,lb (Nt)位比特由激活天线索引携带,则空间调制系统发送一个符号可携带总的数据比特流为lb (Nt)+lb (L)。

在准静态平坦瑞利衰落情况下,假设H为Nr×Nt维的信道矩阵,则接收端的接收信号[11]可以表示为：

y=Hx+n=hjsl+n

(1)

其中:接收向量y=[y1,y2,…,yi,…,yNr]∈CNr×1;x=[x1,x2,…,xNt]T∈CNt×1是发送信号向量且只有一个非零元素sl(sl为星座点集合中的第l个星座点);n∈CNr×1为加性高斯白噪声(Additive White Gaussian Noise, AWGN)向量,里面各元素之间相互独立,且服从均值为0、方差为σ2的复高斯分布。hj表示信道矩阵H∈CNr×Nt的第j列,同时H中的每一个元素hij服从均值为0、方差为1的复高斯分布。

当接收端信道状态信息已知时,根据化简后的接收信号模型,SM系统中的ML检测算法[12]可表示为:

(2)

从式(2)可以看出,ML检测算法穷举搜索了所有天线索引与星座调制符号的组合,虽然性能达到最优,但是当天线数目与调制阶数增大时,复杂度非常高,不适用于实际工程中。文献[10]在传统MIMO系统中提出了一种QRD-M检测算法,该算法通过减少搜索点数来降低复杂度,同时性能达到近似最优。因此本文将QRD-M算法应用到SM系统的信号检测中,并结合SM系统的特点,针对QRD-M算法的不足,提出了一种基于SM系统改进的QRD-M检测算法。

图1 SM系统模型Fig. 1 SM system model

2 SM系统下传统QRD-M检测算法

在SM系统中,本文利用QRD-M算法进行信号检测,该算法利用QR分解将信号检测转换成一个完美的倒置树形搜索,加上M算法,以广度优先方式进行搜索,对每一层的保留节点进行限制,避免搜索所有节点。

在进行信号检测之前,先进行预处理。把信道矩阵H分解成一个Nr×Nt维的酉矩阵Q和一个Nt×Nt维的上三角矩阵R,即H=QR。因此式(1)可表示为:

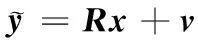
(3)

(4)

因此,式(3)可以表示为:

(5)

其中:rj为上三角矩阵R的第j列。

因此,式(5)可等价为对一个(Nt+1)层的倒置树结构进行搜索。具体搜索过程如图2所示,以调制阶数为4-QAM、收发天线为4×4的SM系统为例。其中第5层为4根发射天线序号;每根发射天线分别引出对应4-QAM调制符号集合的4个节点{s1,s2,s3,s4};黑点表示保留的节点,实线表示累积分支度量值最小的路径。

由图1可知,第i层第j分支的分支度量为:

(6)

第i层第j分支的累积分支度量为:

(7)

QRD-M检测算法从上往下进行搜索,将每层累积分支度量值进行排列,保留最小的M个分支,其余分支则删除,同时将保留下来的M个分支对应的天线索引与调制符号作为下一层的候选节点,进行扩展。到i=1时停止搜索,将M条路径中最小累积分支度量所对应的天线索引与调制符号作为估计值。

图2 QRD-M检测算法树形结构(4×4,4-QAM,M=2)Fig. 2 Tree structure diagram of QRD-M detection algorithm (4×4,4-QAM,M=2)

3 改进的QRD-M算法

传统的QRD-M检测每层都保留固定的节点数,但是每层所保留的节点数直接影响计算的复杂度及性能。当保留的节点数少时,计算复杂度会变小,但同时性能会变差;相反如果保留节点数大时,性能会变好,然而复杂度就会变高。因此关于对保留节点数的选择至关重要,只有选择合适的保留节点数,才能在性能和复杂度之间取得较好的折中。但是目前对于保留节点数的选取并没有明确的标准,一般都是通过大量的仿真得到。基于此种现象,本文对QRD-M算法作出一些改进,提出以下两种算法。

3.1 LC-QRD-dM算法

为了在性能和复杂度之间取得较好的折中,提出一种动态值M的低复杂度的动态M值QRD-M检测算法,即LC-QRD-dM算法。该算法在每一层检测时,设计一个阈值来决定保留的节点数。该阈值用最小累积分支度量和噪声方差来确定,因此第i层的阈值可以被表示为：

(8)

3.2 CS-QRD-dM算法

基于上述改进来说,无论信道好坏与否每层保留的节点最大都不超过M,因此当信道衰落较深时会产生较大的误码率(Bit Error Rate, BER)。为了使信号检测算法在信道衰落较深具有较好的检测性能,进一步提出一种基于信道状态的动态M值QRD-M检测算法,即CS-QRD-dM算法。同样利用LC-QRD-dM算法的思想进行判断,但不同的是,在信噪比较低时,如果候选节点大于M时,则保留全部候选节点数,而小于M时,则保留M个节点;而在信噪比较高时,则按照LC-QRD-dM检测算法进行检测。本文以信噪比15 dB为例:在低于15 dB时,如果候选节点大于M则保留全部候选节点数,而小于M时则保留M个节点；在高于15 dB时,用LC-QRD-dM检测算法进行检测。由于信噪比计算较复杂,可以将其转化为对信道矩阵范数的计算。

4 复杂度分析

4.1 ML检测算法

根据文献[13], ML检测算法计算复杂度为：

CML=6NtNrL

(9)

4.2 QRD-M检测算法

CQRD-M=6[NtL+M2(Nr-1)]

(10)

4.3 改进的QRD-M检测算法

假设在改进的QRD-M检测中,对于提出的LC-QRD-dM检测算法和CS-QRD-dM检测算法,它们每层保留节点数分别表示为Mi、Mj,则计算复杂度分别为：

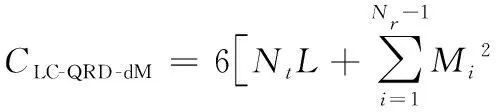
(11)

(12)

由上面的分析可见,ML检测算法的复杂度最高。由于LC-QRD-dM检测算法每层保留的节点数最大不超过M,因此计算复杂度远低于传统QRD-M检测算法。对CS-QRD-dM检测算法来说，其复杂度表达式与LC-QRD-dM检测算法相同,但是在低信噪比时,由于保留的节点数大于传统QRD-M算法与LC-QRD-dM检测算法,因此复杂度相对传统QRD-M检测算法来说有所提高；而在高信噪比时,其保留的节点数与LC-QRD-dM检测算法相同,因此计算复杂度远小于传统QRD-M检测算法。

5 仿真结果与分析

在Matlab环境下对上述算法进行软件仿真,并在不同的条件下进行性能的比较。仿真过程中,信道状态信息已知,且采用准静态平坦瑞利衰落信道。

如图3所示,在收发天线分别为4×4、8×8,且Mi最大值为4,采用4-QAM调制的情况下,对LC-QRD-dM算法在不同X值的条件下进行的仿真。由图3可知,在不同的收发天线配置下,LC-QRD-dM算法依然适用,且当X不同时,提出的LC-QRD-dM算法性能会有所差异,X值越大,检测的性能越好,搜索的节点数越多。值得注意的是,随着X的增大,性能改善的程度将缩小。因此可以根据实际应用中的不同要求,在检测性能与计算复杂度之间取得较好的折中。

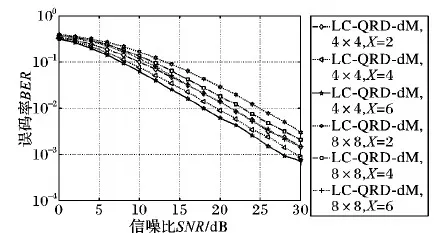
图3 LC-QRD-dM算法中不同X值的误码率比较Fig. 3 BER comparison for different X values in LC-QRD-dM algorithm

图4给出了在4×4系统下,采用4-QAM调制对ML算法、传统QRD-M算法及LC-QRD-dM算法进行仿真的结果。为了有效地进行算法的验证,在计算复杂度与性能之间取得较好的折中,在4×4系统下,本文选择X为8。对于传统QRD-M算法分别选择保留节点M为2和4,同时为了更好地与传统QRD-M检测算法相比,LC-QRD-dM算法的最大值M,即Mmax分别取2和4。当Mmax为4,BER=10-2时,LC-QRD-dM算法与传统QRD-M算法和ML算法仅相差2 dB和5 dB。LC-QRD-dM算法与传统QRD-M算法相比检测性能略有下降,但是此时LC-QRD-dM算法的计算复杂度远远低于传统QRD-M算法。当取Mmax为2时,LC-QRD-dM算法性能近似于传统的QRD-M算法,虽然与ML检测算法相比性能有所下降,但是LC-QRD-dM算法的计算复杂度远远低于全搜索的ML检测算法。

图4 ML、QRD-M和LC-QRD-dM算法的误码率对比Fig. 4 BER comparison of ML, QRD-M and LC-QRD-dM

图5给出了在4×4系统下,采用4-QAM调制,对传统QRD-M算法、LC-QRD-dM算法及CS-QRD-dM算法进行性能仿真，其中传统的QRD-dM算法选择的保留节点M为4。由图5可知,以信噪比15 dB为界,在信噪比低于15 dB时,所提出的CS-QRD-dM算法以增加一定计算量为代价,其检测性能明显优于传统QRD-M算法,特别是在误码率为10-2时,信噪比提高了约1.3 dB;在信噪比高于15 dB时,CS-QRD-dM算法与LC-QRD-dM算法类似,以牺牲少量性能为代价,大幅降低了计算的复杂度。

图5 CS-QRD-dM、QRD-M和LC-QRD-dM算法的误码率对比Fig. 5 BER comparison of CS-QRD-dM, QRD-M and LC-QRD-dM

6 结语

在SM系统中,由于ML检测算法穷举搜索所有的天线索引与数字调制符号组合,导致计算复杂度过高，由此提出了QR分解与M算法结合的QRD-M检测算法———LC-QRD-dM。该算法将信号检测变为树形结构搜索的过程,采用宽度优先的方式进行检测,避免了对所有节点的搜索；但是由于在不同的信噪比下,每层都保留固定的M个最小累积分支度量值,一定程度上会造成计算量的增加。因此,本文针对上述问题对M值的选择设计一个阈值,动态地选择保留节点数,使保留节点数最大为M,这样可以有效地降低计算复杂度,同时性能接近QRD-M检测算法;但信道无论在任何状态下,每层所保留的节点数都不大于M,因此在信道衰落较深时,会产生较大的误码率。针对该问题,又引入基于信道状态的动态M值QRD-M检测算法——CS-QRD-dM，该算法在低信噪比时,相对于传统QRD-M检测算法性能明显得到提升；在高信噪比时,其性能和复杂度与低复杂度的动态M值QRD-M检测算法相同。