不同姿态解算在平衡车中的实现与应用

贵阳学院电子与通信工程学院 古 训 陈 红

双轮平衡车是一种基于“动态稳定”的两轮机器人，它利用车载陀螺仪和加速度计传感器实时检测车身姿态，控制电机的转速使平衡车保持动态稳定。利用MPU6050常用的姿态解算有一阶互补滤波、二阶互补滤波、匹配滤波以及卡尔曼滤波等算法。本文分别对四种算法进行分析以及实验验证，获取最佳的姿态解算方案，完成平衡车姿态角度的最佳估计，实现平衡车直立的动态稳定。

0 引言

随着城市经济的发展，城市交通需求迅速增长。为了解决城市交通的问题，引进了新的代步工具——平衡车，它体积小，便于携带，同时采用电能驱动，节能、环保，提高了人们出行的效率。平衡车主要利用车载传感器检测车体姿态角度的变化，然后通过控制系统驱动电机，达到两轮直立自平衡的效果。

本文通过MPU6050模块（赖义汉,王凯.基于MPU6050的双轮平衡车控制系统设计[J].河南工程学院学报(自然科学版),2014,26(01):53-57）获取加速度和角速度，对车体姿态进行识别。MPU6050模块为整合性6轴运动处理组件，内置3轴陀螺仪，3轴加速度计，如图1所示。其中陀螺仪输出的角速度积分就可以得到角度值，但是由于角速度存在微小的偏差和漂移，经过积分运算之后就会形成累积误差。加速度计恰好和陀螺仪特性相反：没有累积误差。但是由于平衡车在运动时，极易受到外部的干扰，采集加速度值时会产生很大的噪声信号。所以单独使用陀螺仪或加速度计估计平衡车的姿态是很难实现的。因此需要采用滤波算法将其加速度计和陀螺仪之间的数据进行融合，计算出平衡车偏转角度的最优估计值，完成平衡车的姿态解算。

图1 MPU6050模块

本文采用四种不同的姿态解算算法对平衡车姿态进行解算，对比不同姿态解算的效果以及在平衡车上的应用，选出平衡车姿态的最优估计，完成平衡车的姿态解算。

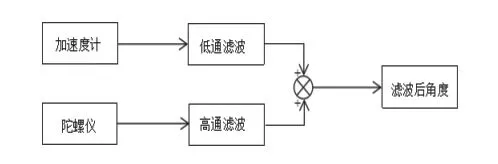
图2 一阶互补滤波算法框图

1 四种姿态解算的应用

1.1 一阶互补滤波

一阶互补滤波（付勇杰,丁艳红,梁义维,行阳阳.动态倾角传感器及其传递特性的研究[J].仪表技术与传感器,2012(09):6-8）融合了陀螺仪提供的高频角速度信号和加速度计提供的低频角度信号，采用高通滤波算法抑制陀螺仪的积分漂移,低通滤波算法除去加速度计短时间快速变化的信号，分别滤出相应的噪声信号，补偿陀螺仪的累积误差和加速度的动态误差，得到平衡车姿态的估计值。算法框图如图2所示。

一阶互补滤波的表达式（梁光胜,杜梦楠,周子豪,刘春旭,文月.基于互补滤波的两轮自平衡车姿态控制[J].测控技术,2015,34(05):72-74）如公式(1)所示。

上式中，anglen为第n次滤波后的角度，anglen-1为第n-1次滤波的角度，a为加速度取值的权重，其取值范围为0～1，angle_m为加速度计的采样值，gyro_m为陀螺仪的角速度采样值，dt为采样时间。

经过参数调整，最终得到当a=0.08时，其滤波效果如图3所示。其中曲线1表示滤波前的角度量纲值，曲线2为滤波后的角度量纲值（图5、7、9中曲线1和曲线2的含义同图3）。

图3 一阶互补滤波前后曲线

1.2 二阶互补滤波

二阶互补滤波算法（南余荣,宛冬晴,潘帅,姚亚楠.二阶互补滤波姿态求解器的设计[J].浙江工业大学学报,2017,45(04):416-420）主要是在一阶互补滤波算法的补偿环节加入积分器，消除陀螺仪漂移误差，其原理框图如图4所示。

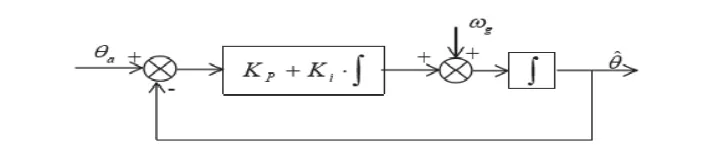
图4 二阶互补滤波原理图

其中，ωg为陀螺仪测量的角速度，θa为加速度计测量的角度值，Kp为比例系数，Ki为积分系数，其中。

时域微分形式如公式(2)所示。

经过参数整定，最终当加速度计取值的权重k=0.78时，其滤波效果如图5所示。

1.3 匹配滤波

匹配滤波（龚晓辉,薄祥岑.基于MC9S12XS128的二轮直立车设计与实现[J].电子设计工程,2014,22(02):137-139）主要是利用加速度计所获得的角度θg与陀螺仪积分后的角度θ进行比较，将比较的误差信号经过比例Tg放大，然后与陀螺仪输出的角速度信号叠加，再进行积分。对于加速度计给定的角度θg，经过比例、积分环节使产生的角度θ最终等于θg。这样就可以消除陀螺仪的累积误差，其算法框图如图6所示。

图5 二阶互补滤波前后曲线

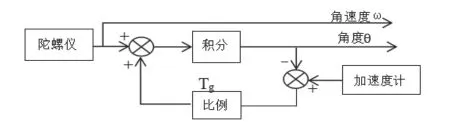
图6 匹配滤波算法框图

通过修改Tg，改变其滤波的效果，最终当Tg=0.08时，得到最佳的滤波效果，如图7所示，其中曲线1为滤波前的角度量纲值，曲线2为滤波后的角度量纲值。

图7 匹配滤波前后曲线

1.4 卡尔曼滤波

卡尔曼滤波（彭丁聪.卡尔曼滤波的基本原理及应用[J].软件导刊,2009,8(11):32-34）（Kalman filtering）是利用线性系统状态方程通过系统输入输出观测数据对系统状态进行最优估计的算法。其主要思想是：以最小均方误差作为最优估计准则，利用信号与噪声的状态空间模型，利用前一时刻的估计值和当前时刻的观测量，更新对状态变量的估计，并计算当前时刻的估计值。

卡尔曼滤波的递推过程（杨凌霄,李晓阳.基于卡尔曼滤波的两轮自平衡车姿态检测方法[J].计算机仿真,2014,31(06):406-409）如公式(3)所示。

上式中，AK为系统矩阵，BK为控制输入矩阵，HK为测量矩阵，KK为卡尔曼增益，PK为误差的协方差矩阵，Q为过程噪声协方差矩阵，R为测量噪声协方差矩阵。

卡尔曼滤波的系统模型框图如图8所示。

图8 卡尔曼滤波系统模型框图

通过调节Q_angle、Q_gyro、R_angle三个系数，可以修改其滤波效果，经过一系列的参数调整、实验最终得到如表1所示的参数，其滤波效果如图9所示。

表1 卡尔曼可调参数

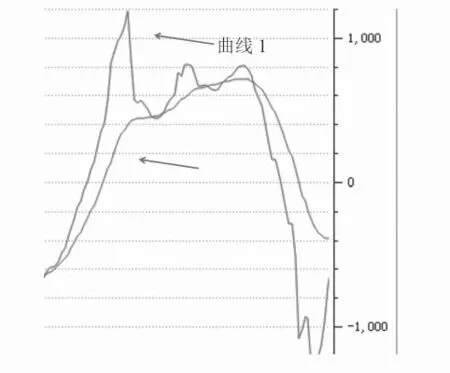
图9 卡尔曼滤波前后曲线

2 四种姿态解算在平衡车上的实际对比

2.1 四种姿态解算的滤波曲线

图10至13是四种滤波方案在相同情况下的滤波效果比对，曲线1为一阶互补滤波，曲线2为二阶互补滤波，曲线3为匹配滤波，曲线4为卡尔曼滤波方案。

将平衡车快速倾斜，静止，然后快速回位，得到图10的曲线。采用这种方式主要是为了测试平衡车倾角在剧烈变化时，曲线的平滑效果。从图上可以看出，四条曲线的收敛速度差不多，但是从平滑效果上看，曲线1与曲线3的平滑效果不是很好，有严重的超调现象，其中平滑效果最好的是曲线2，曲线4的平滑效果比较适中。

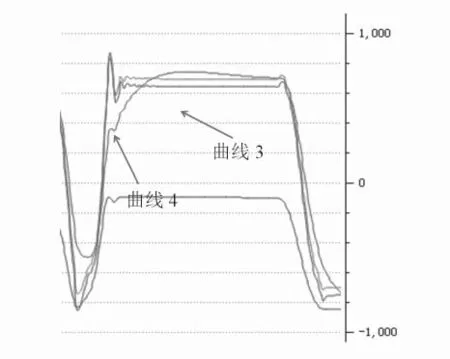
图10 快速倾斜、静止、回位

将平衡车缓慢倾斜，静止，然后缓慢回位，得到图11的曲线。采取这种方式主要是为了测试平衡车倾角的跟随性，即曲线的收敛速度。从图上可以看出，曲线1、3、4的收敛速度差不多，响应都很灵敏，曲线2有点滞后。

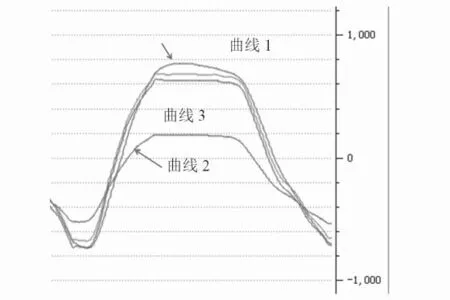
图11 缓慢倾斜、静止、回位

图12是平衡车在原地小弧度的高频抖动时，得到的曲线图。主要是为了测试平衡车直立时的高频震荡时，四条滤波的滤波效果。从图12上，我们可以发现曲线1、3的波动很大，其滤波效果很差，曲线4有小幅度缓慢的起伏，相对于曲线1、3、4，曲线2的滤波效果是最好的。

图12 小弧度的高频抖动

图13是模仿平衡车在水平面上水平移动，可以观测到曲线1、3的波动大，滤波效果相对于曲线2、4效果不是很好。

图13 水平移动

综上四个图来看，曲线1——一阶互补滤波的收敛速度虽然很快，但是其平滑效果很差；曲线2——二阶互补滤波的平滑效果虽然最好，但是收敛速度相对其他三种滤波方案要慢；曲线3——匹配滤波的滤波效果和一阶互补滤波的滤波效果差不多，收敛速度快，但是曲线的平滑效果不是很好；与之相比，曲线4——卡尔曼滤波的收敛速度和平滑效果平衡得较好，比较适中。

2.2 四种姿态解算的时间对比

表2是四种滤波方案的滤波所执行的时间表，采用定时器中断的方法，测量四种算法执行所需要的时间，由于卡尔曼滤波算法相对其它三种滤波要复杂的多，所以其滤波所需的时间相对较长，而一阶互补滤波算法是最简单的，所需的时间最短。

表2 四种滤波解算执行时长

2.3 四种姿态解算在平衡车上应用

本文利用四种姿态解算实现平衡车的动态直立稳定，观测四种姿态解算在平衡车动态直立时，突然受到外界干扰平衡车的动态效果。

通过这个实验测试发现一阶互补滤波和匹配滤波在受到外界干扰时，平衡车会在原地附近高频的前后抖动，经过一段时间后才能趋于稳定。以此说明了一阶互补滤波和匹配滤波响应速度很快，但是由于存在角度超调的现象，使平衡车在突然受到外界干扰时会产生高频的来回抖动，不能快速的回到平衡位置。相对于一阶互补滤波和匹配滤波，二阶互补滤波特性恰好与这两种滤波相反。采用二阶互补滤波时，如果平衡车突然受到外界干扰，平衡车回到平衡位置的收敛速度没有阶互补滤波和匹配滤快，但是二阶互补不会出现超调、来回抖动的现象。而卡尔曼滤波恰好融其了三种滤波的特点，在受到外界干扰时，使用卡尔曼滤波算法的平衡车能够快速的回到平衡位置。

综上，从平滑角度上看，匹配滤波和一阶互补滤波的平滑效果没有卡尔曼滤波的效果好；从收敛速度上看，二阶互补滤波的收敛速度没有卡尔曼滤波的收敛速度快；从滤波所需时间上看，卡尔曼滤波相对其他曲线所需时间较长；从动态直立的效果上看，卡尔曼滤波综合了其它三种滤波的优势，在受到外界干扰时快速的回到平衡位置。结合平滑效果、收敛速度和直立的动态效果，最终采用卡尔曼滤波的方案对角度进行滤波，完成平衡车的姿态估计，实现平衡车的动态稳定，如图14所示。

图14 平衡车的直立效果

3 结束语

本文主要对四种滤波解算在平衡车上的滤波效果做出了相应的阐述，分析其四种滤波解算的滤波原理和实验效果，以及对比四种滤波方案的滤波效果和动态平衡效果，选出了本次姿态解算的最佳滤波方 案，获得平衡车姿态的最优估计，实现了平衡车的动态稳定，为后续的相关平衡车控制系统的研究打下基础。