基准站分布对航空重力测量精度影响分析

尹伟言，陈 真，聂 晶,陈小英，赵 鑫

(1.国家测绘地理信息局第一大地测量队，陕西 西安 710054；2.国家测绘地理信息局测绘标准化研究所，陕西 西安 710054)

航空重力测量系统以飞机为平台，包括重力仪、GPS系统、姿态传感器等。其中，GPS系统用于获取时间、空间三维坐标、速度和加速度等信息，为重力传感器获取的总加速度提供各种改正[1-3]。航空重力测量中载体的动态定位、动态测速、加速度测定均需要由GPS完成。动态定位是指用于指导飞行员按照设计航线行进，由于重力异常计算时需在一定时间间隔内进行平滑，故对定位精度要求不高。重力在平面位置上的变化每km约为1～5×10-5m/s-2，因此平面精度百米级即可满足要求。动态测速是通过建立相位率测量值和载体速度之间的数学关系，利用原始载波相位值计算载体运动速度。该方法避免周跳，速度精度在垂向方向的绝对精度可达0.01～0.02 m/s。加速度测定可用两种方法:一是在位置域内对位置信息做二次微分或对速度信息做一次微分，该方法需要较高的定位精度和速度精度，利用载波相位测量技术实现；二是对载波相位观测值二次微分后获取载波相位加速度序列，建立相位加速度和载体速度之间的数学关系，求取载体加速度的估值，该方法精度高，可避免整周模糊度的确定[4-6]。

不同的基准站距离，在确定载体位置、速度和加速度时有明显差异，在计算测线高度处的重力异常时，与厄缶改正、垂直加速度、水平加速度都有着直接关系。基准站距离通过影响各项改正，进而影响航空重力测量的重力异常及其残差。本文利用航空重力实测数据从位置、速度、重力异常和交叉点不符值4个方面来分析不同基准站距离对航空重力测量的影响，为开展大规模航空重力生产和研究提供参考。

1 数学模型

航空重力测量属于相对测量的范畴，作业前需确定停机坪处的绝对重力值，并将空中观测值fh与地面重力基准值r0进行联合，其基本数学模型为

(1)

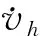
δg=δb+δg*-av-ae-ar+af-r0.

(2)

根据以上理论，航空重力测量中需要计算载体的位置、速度和加速度，而这些量均由GPS获取。

2 基准站布设

航空重力测量中，定位传感器分系统是航空重力测量系统的关键部分，利用其提供的高精度测量信息可分离出引力加速度和惯性加速度。该系统包括硬件和软件两部分，硬件由1套置于飞机上的流动站和至少3套置于测区的地面GPS基准站组成，用于高精度定位和测速，实现高精度差分定位；软件可实现GPS数据检查、处理、格式转换，并能融合姿态文件、速度文件、重力加速度文件获取测线重力异常。

2.1 位置分布

实际作业中，一般要求基准站均匀分布在整个测区内，彼此之间构成良好的几何关系，同时尽量利用测区内已有的高等级GPS点。几种基准站布设如图1所示。

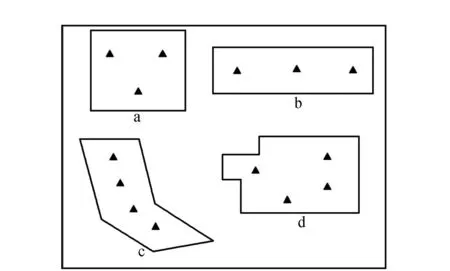
图1 GPS基准站位置分布

通常，对于规则形状的测区，基准站可以均匀分布(如a和b)，如果测区形状不规则，则需要增加基准站数量(如c和d)。

2.2 选址要求

基准站位置的选择条件和静态GPS控制网点的要求基本相同，主要考虑点位的稳固性、环境干扰等因素[11-13]。选址的一般要求见表1。

表1 基准站选址要求

2.3 数据要求

对于每个架次的基准站数据，应利用相关软件进行检查(如TEQC)，确保数据完整和有效。数据采样率应至少达到2Hz，卫星观测数至少6颗，数据可利用率不少于80%，L1、L2频率的多路径效应MP1、MP2应小于0.5 m，接收机日频稳定性不低于10-8等[14-16]。

3 实例分析

本次的实测数据来自GT-2A航空重力测量系统，该系统为莫斯科国立大学研制，属于三轴稳定平台的标量型设备，其重复线内符合精度优于0.6×10-5m/s-2，主、副测线交叉点平差精度优于1×10-5m/s-2。数据处理软件采用配备的GT-Gravity，本软件每次仅能使用1台GPS基站数据，对试验中的两个基站BAS1和NQ02逐个进行计算和分析。

理想状况下，GPS基准站的分布应满足均匀布设的原则，但当测区位于海洋中或者测区架设基准站困难时，应考虑基准站距离对测量结果的影响。本次数据分别采用机场(BAS1)和测区(NQ02)两个基准站对12条主测线和12条副测线进行处理来分析不同基线长度对航空重力测量精度的影响。BAS1基准站距离测区大约600 km，NQ02基准站位于测区内，测区大小为120 km×115 km，主测线和副测线间距均为10 km。基准站分布如图2所示。

图2 试验区基准站分布

分别利用两个基准站BSA1和NQ02获取载体的实时位置、速度信息，并采用相同的滤波方法祛除高频噪声，利用相同的前校和后校数据做漂移改正，获取自由空间重力异常；利用全部测线和检测线处交叉点不符值平差计算，评价测区总体精度。

3.1 位置分析

分别利用基准站BSA1和NQ02计算载体位置在X，Y，Z轴方向的坐标差，结果如图3—图5及表2所示。

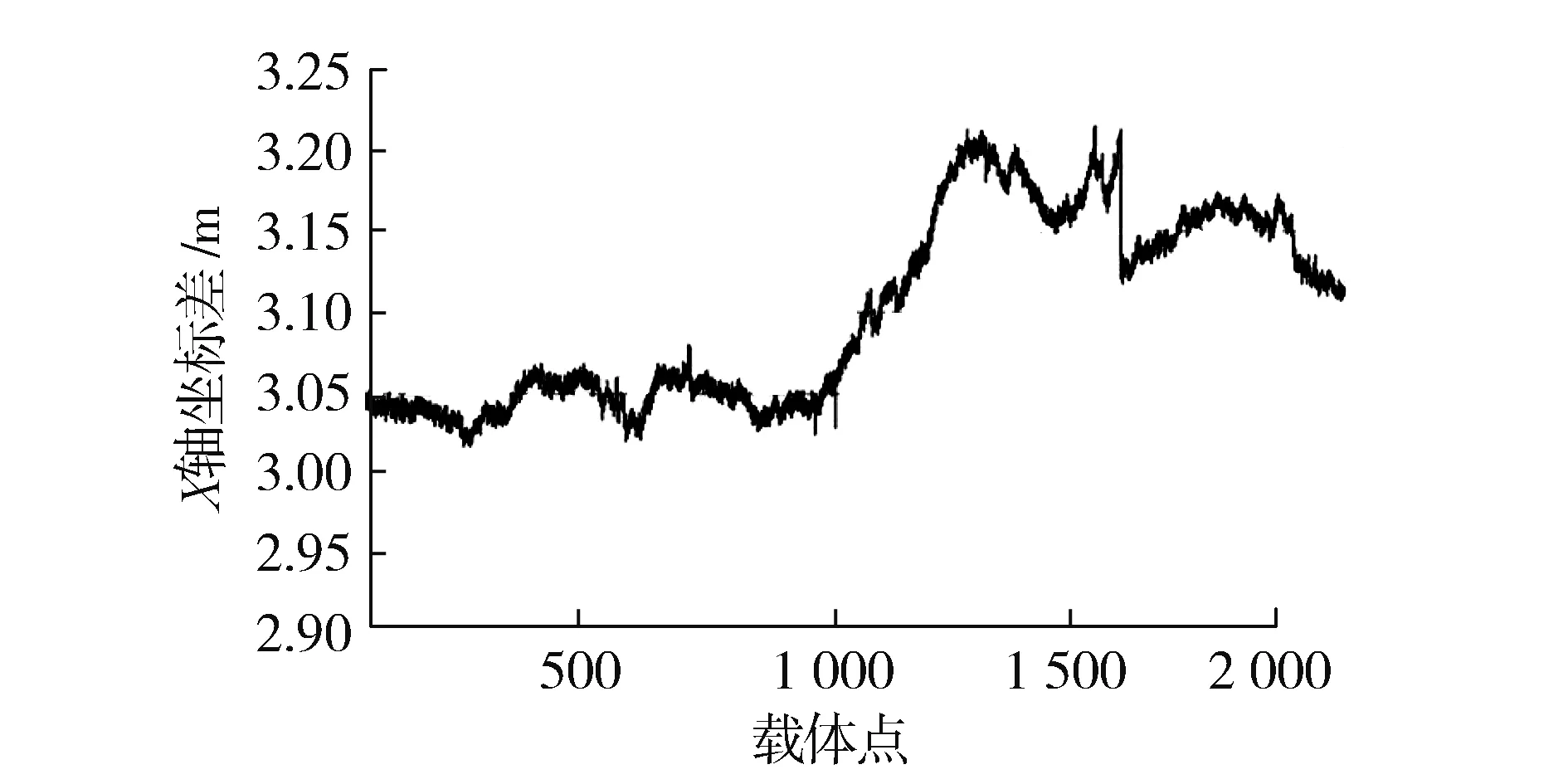
图3 两基准站在X轴方向坐标差

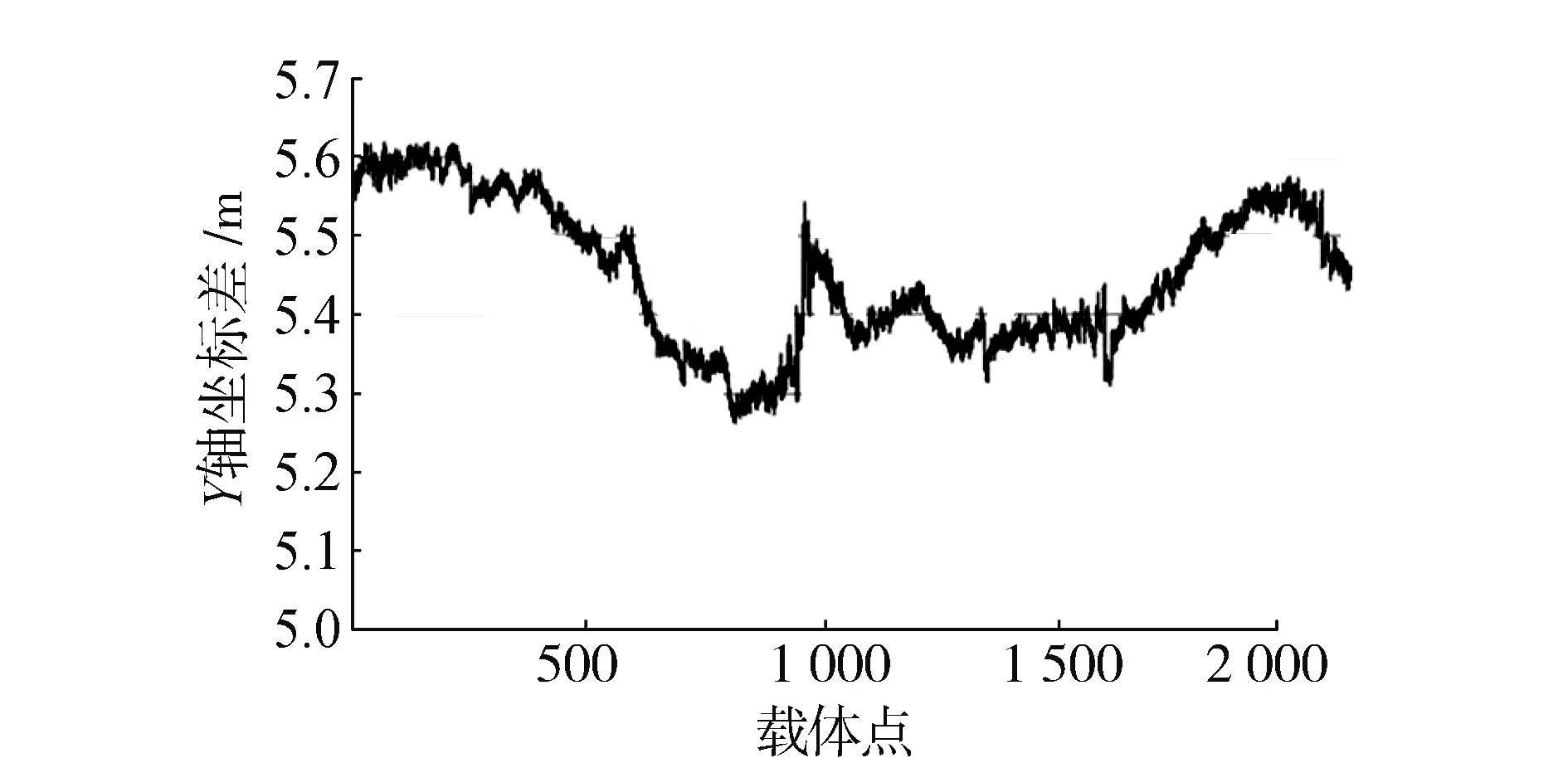
图4 两基准站在Y轴方向坐标差

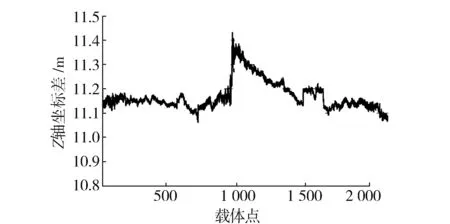
图5 两基准站在Z轴方向坐标差

从以上统计看出：在距离600 km的两台基准站中，载体实时的定位坐标在X轴方向上相差3.1 m左右，在Y轴方向上相差5.4 m左右，在Z轴方向上相差约11.2 m。这说明GPS动态定位在水平方向约4.3 m，而在高程方向要差一些，约11 m。

3.2 速度分析

分别利用基站BSA1和NQ02计算载体速度在N,E,U轴方向之差，结果如图6—图8及表3所示。

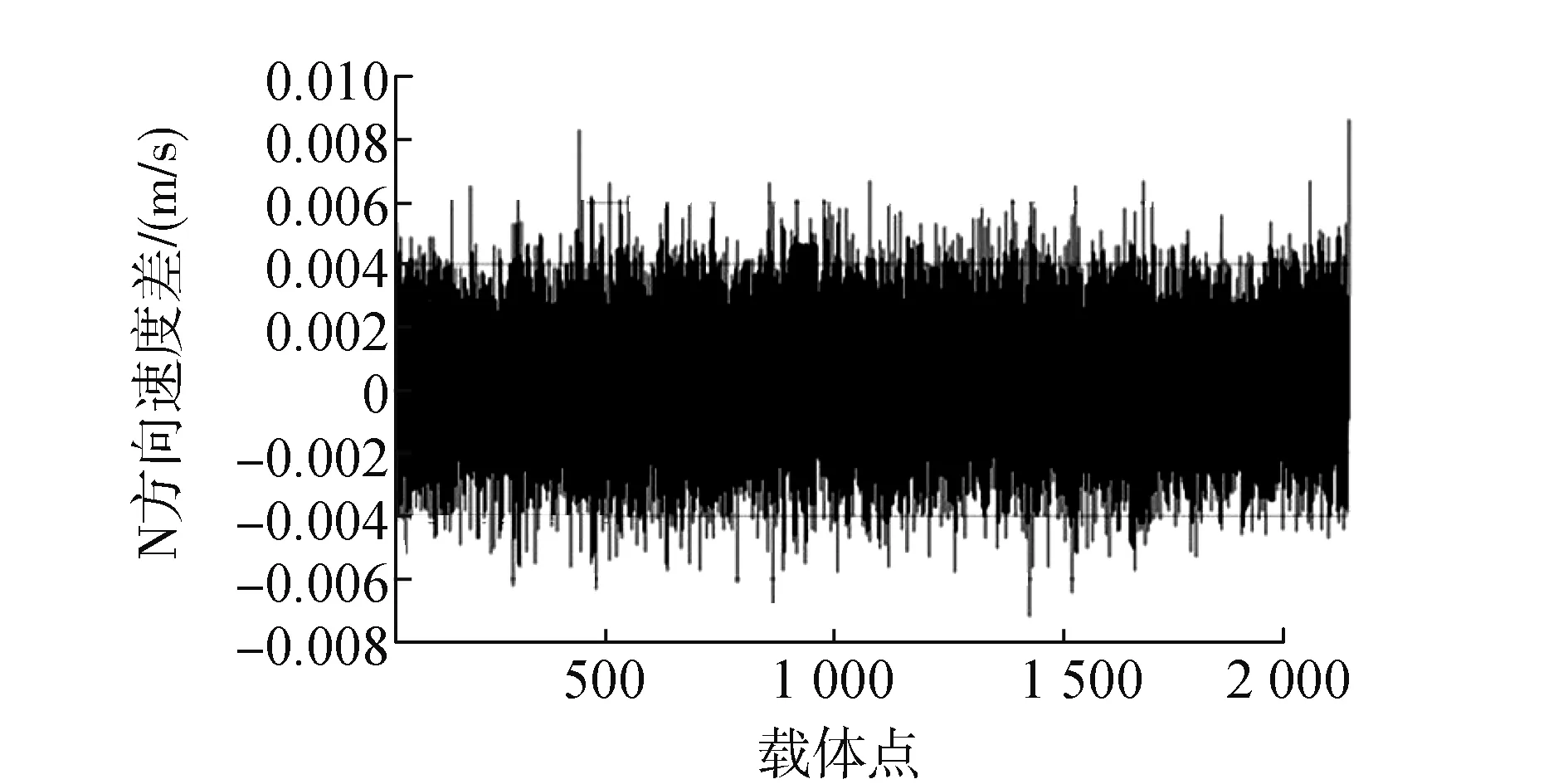
图6 两基准站在N轴方向速度差

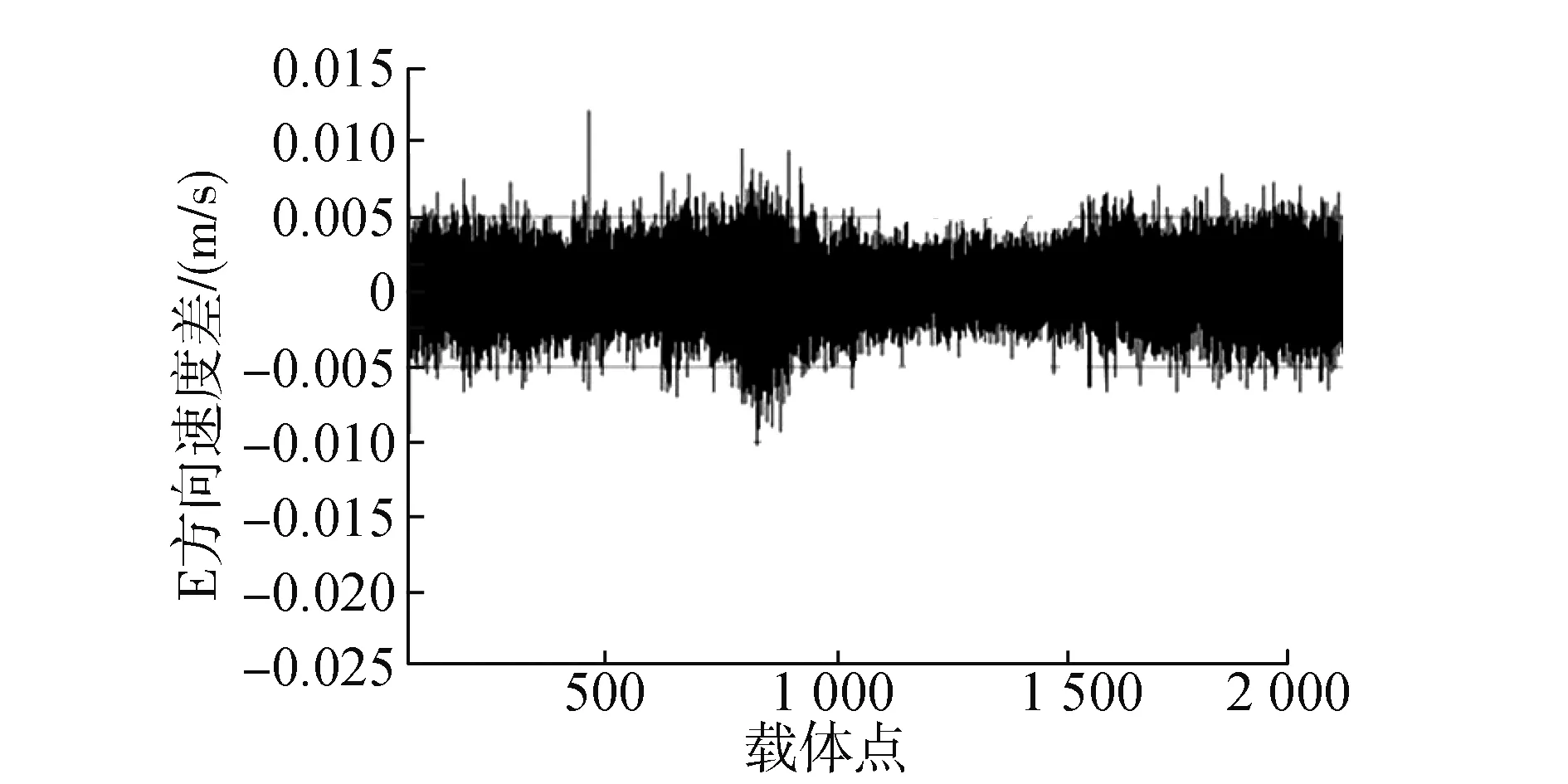
图7 两基准站在E轴方向速度差

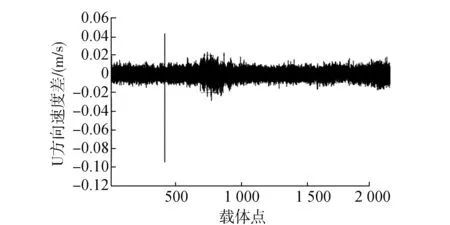
图8 两基准站在U轴方向速度差

10-5 m/s

通过以上分析可知：除了U方向存在瞬间粗差外，两台基准站获取的速度非常接近，在3个方向上相差约0.000 3 1m/s，这说明600 km远的基准站所确定的载体速度与测区内的基准站获取的速度相差不大。

3.3 重力异常分析

对于两台基准站获取的重力异常，分别利用100 s窗口的自适应Kalman滤波进行去噪处理，获得最终的重力异常，并计算滤波前后的残差值。两台基准站下最终重力异常差异以及残差差异如图9、表4和图10所示。

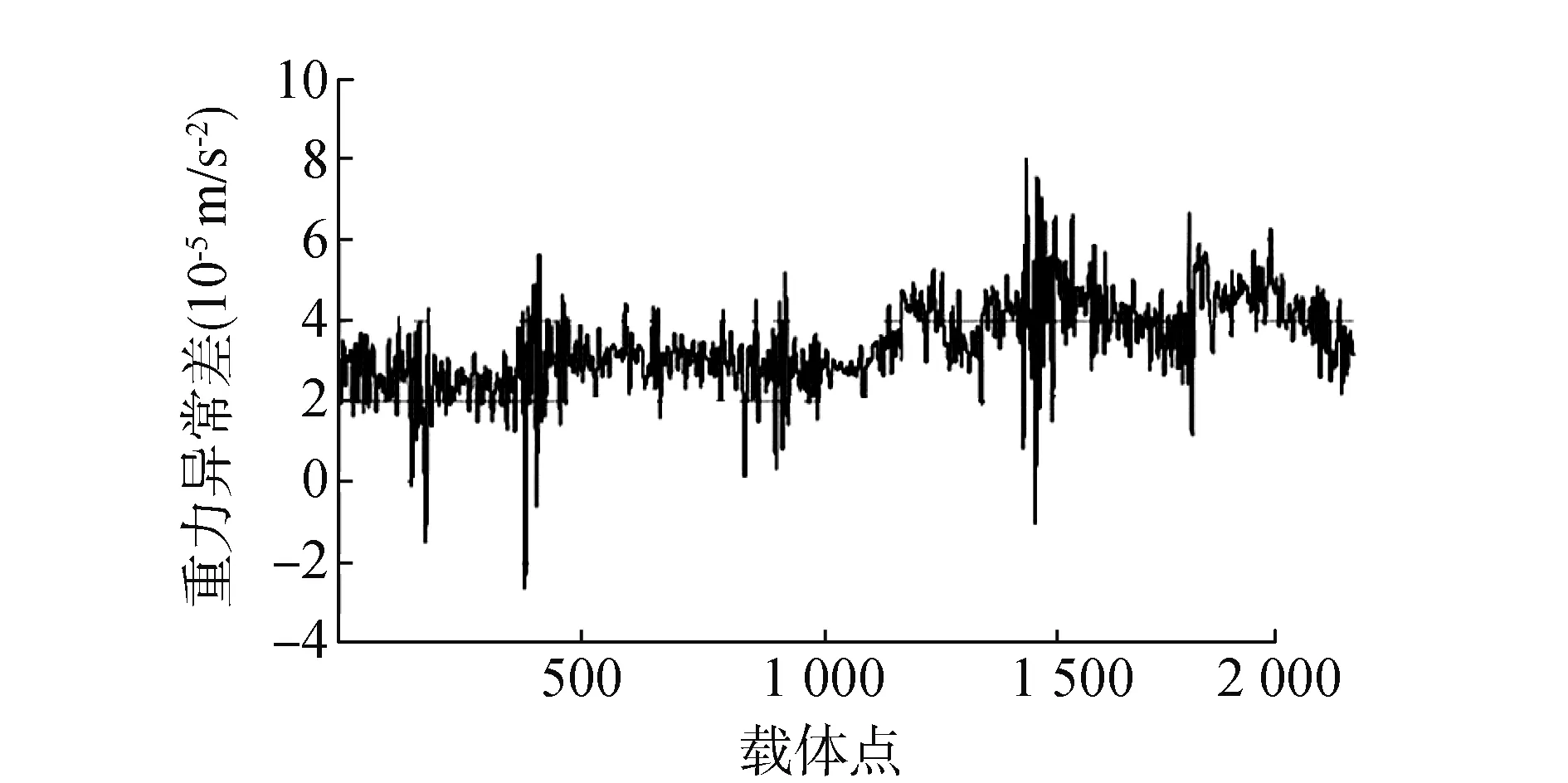
图9 两基准站重力异常差

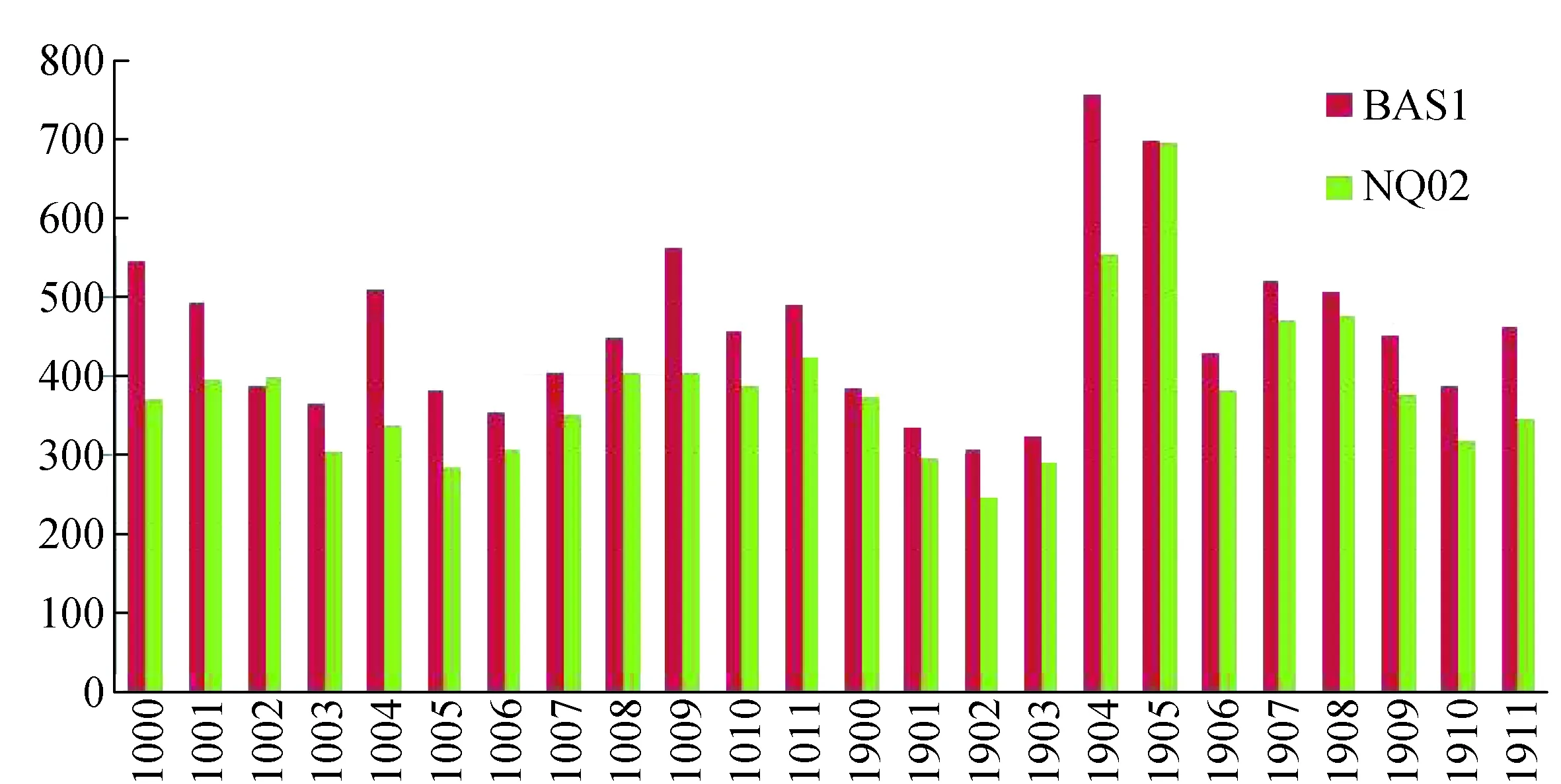
图10 两基准站下自由空间重力异常残差(10-5 m/s-2)

由以上分析可知：不同基准站下的重力异常差距明显，平均在3.4×10-5m/s-2，考虑到平差后总精度一般要求优于1×10-5m/s-2，故该量级的差距不容忽视；同时，BAS1的残差明显大于NQ02的残差，其中5条测线的差距超过100×10-5m/s-2，这说明基线的长短通过影响GPS测量，从而影响航空重力测量中各项改正的确定精度(如厄缶改正、水平加速度以及垂直加速度)，致使滤波后的残差较大。

3.4 交叉点不符值分析

分别用BAS1和NQ02完成12条测线和12条检测线自由空间重力异常交叉点不符值的计算，如图11所示。其中，黑色圆点表示<1×10-5m/s-2、红色圆点表示1～2×10-5m/s-2、绿色圆点表示2～3×10-5m/s-2、蓝色圆点表示3～4×10-5m/s-2。重力异常交叉点不符值统计见表5。

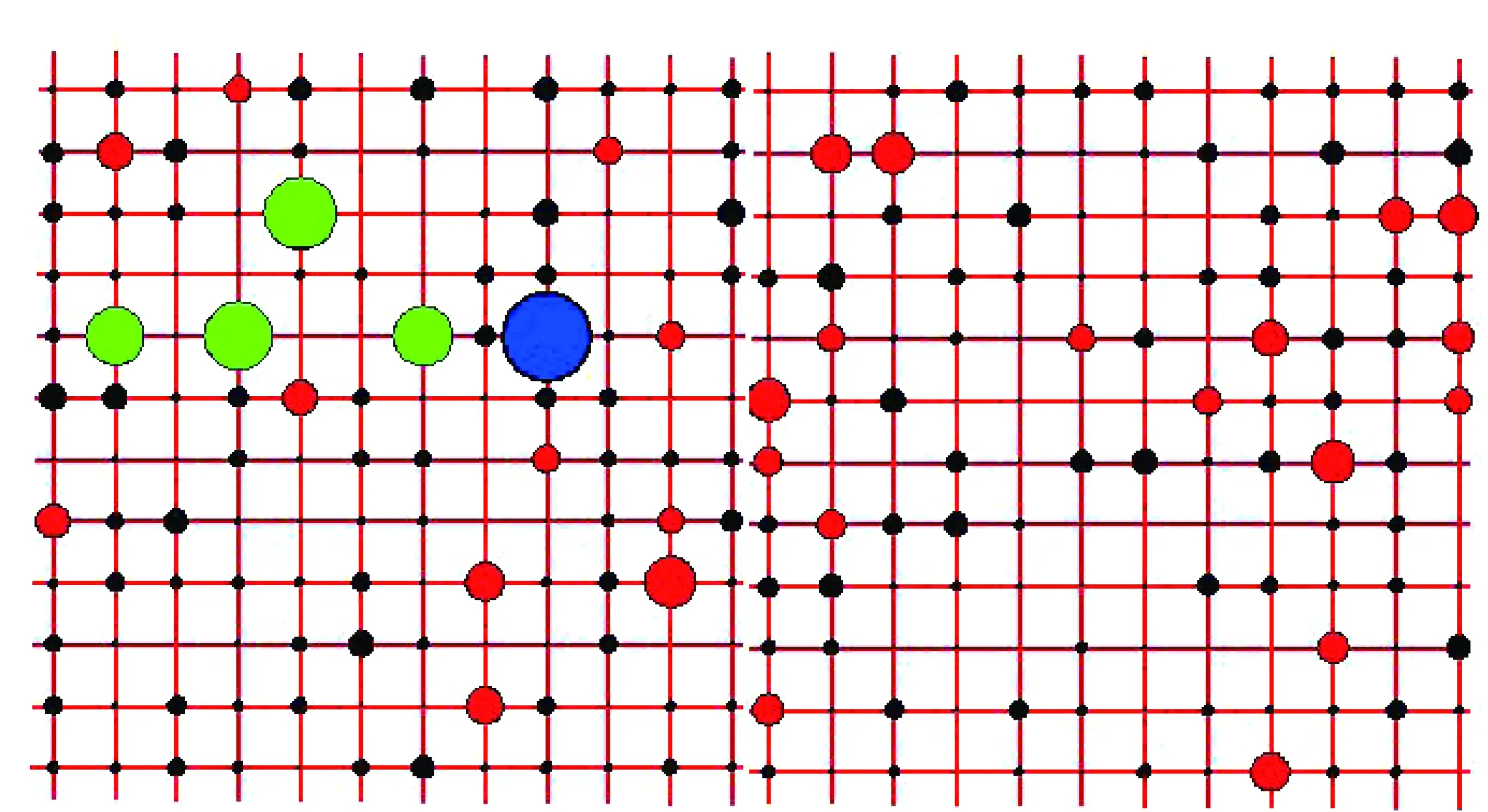
图11 BAS1(左)和NQ02(右)基准站交叉点不符值

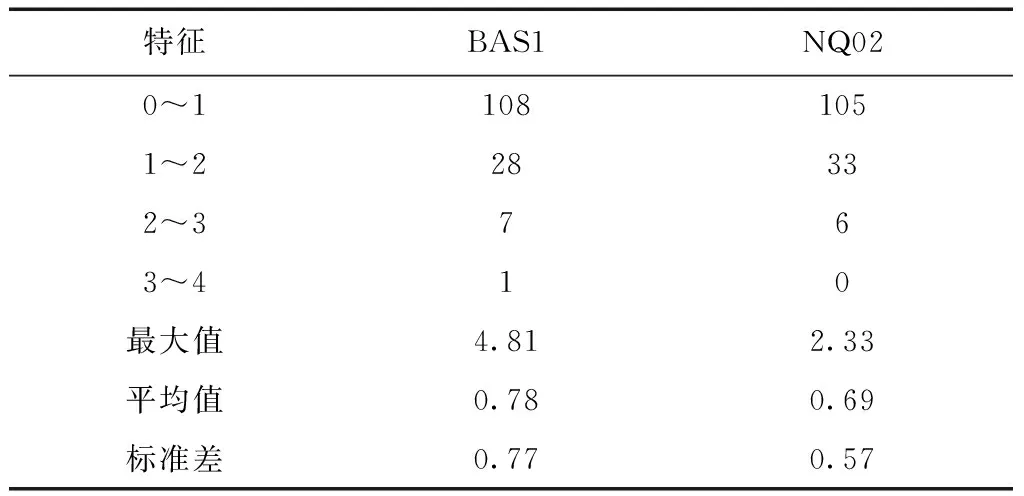
经分析，两种基准站自由空间重力异常交叉点不符值在0～1×10-5m/s-2之间的占据主要部分，且最终标准差均在1×10-5m/s-2以内，说明两种基准站解算结果均符合要求；但同时，NQ02基站中最大不符值和均值均明显小于BAS1，并且通过标准差直观反映NQ02解算精度比BAS1有明显提高。

4 结 论

利用航空重力实测数据从位置、速度、重力异常和交叉点不符值4个方面来分析不同基准站距离对航空重力测量的影响，得到如下结论：

1)GPS基准站的布设位置对航空重力测量精度有较大的影响。

2)基准站距离过长时，对实时位置的影响可超过10 m(Z轴方向)；对最终重力异常的影响为3～4×10-5m/s-2；对滤波残差的影响尤为明显，可使多条测线残差超过100×10-5m/s-2；对空间异常的影响较为显著，交叉点不符值分别为0.78×10-5m/s-2和0.69×10-5m/s-2，致使最终精度分别为0.77×10-5m/s-2和0.57×10-5m/s-2。

3)在航空重力测量项目实施过程中应着重考虑基准站布设问题，基准站优先选择在测区中央，对于较大测区或布设困难地区，可适当增加基准站数量。