车用发电机定子绕组匝间短路故障下转子弯扭耦合振动特性分析
许小伟,王红霞,严运兵,王维强
(武汉科技大学汽车与交通工程学院,湖北 武汉,430065)
增程式电动汽车是在纯电动汽车基础上加载增程器来提高续驶里程,被认为是目前最理想的电动汽车过渡类型[1]。增程器为发动机和发电机的耦合组件,大多采用三相交流永磁同步发电机,发电机一旦发生故障会影响增程器及整车的性能。发电机所有故障中定子绕组匝间短路发生率比较高,运行环境及工况变化、机械振动等因素都可能导致这一故障[2-4]。匝间短路会破坏发电机对称性,产生短路环流使线圈局部温度升高,进而引发相间短路故障,增强转子的径向振动,对发电机本身运行的稳定性造成严重影响[5-7]。因此,研究发电机定子绕组匝间短路故障下转子弯扭振动特性具有非常重要的意义。
目前,对于发电机定子绕组匝间短路故障研究大多采用有限元法,通过场路耦合理论及多回路理论建立发电机有限元模型,并借助有限元工具软件分析故障后电参数的变化。赵洪森等[8]基于场路耦合原理建立发电机有限元模型,研究了定子内部短路故障前后电磁转矩在稳态过程和瞬态过程中的变化特征,以及在不同短路匝数与短路位置时电磁转矩变化的规律性。戈宝军等[9]利用电磁场有限元分析法,研究了不同短路匝比时发电机不平衡径向电磁力幅值的变化规律。叶志军等[10]和付朝阳等[11]在定子绕组故障理论分析基础上,运用有限元模型对匝间短路故障进行诊断并分析故障后发电机相电流的故障特性。有限元法主要研究匝间短路故障系统电参数的变化,对故障系统的故障机理及机械参数的分析比较少,目前对于故障机理分析大多采用数值积分法。宋志强等[12]建立发电机转子弯扭耦合振动模型,运用数值积分法研究了弯扭电磁刚度对转子弯扭振动幅值的影响规律。苟东明等[13]利用数值分析法研究了水轮发电机定转子碰摩系统非线性动力特性与系统参数之间的关联。以上研究主要运用数值积分法分析了发电机未发生故障时转子系统的弯扭耦合振动特性,但对于定子匝间短路故障下转子的弯扭耦合振动特性研究却比较少。
为此,本文运用数值积分法,在建立发电机转子系统弯扭耦合振动模型基础上,考虑定子绕组匝间短路故障时发电机转子弯曲及扭转电磁刚度的影响,对不同程度匝间短路故障下转子的弯曲及扭转振动特性进行分析,以期为发电机定子绕组匝间短路故障的诊断提供参考。
1 匝间短路时转子系统的弯扭耦合振动模型
1.1 发电机转子系统弯扭耦合振动模型
假设发电机转子可简化为质量为m的轮盘,忽略大轴的质量,发电机转子-轴承系统示意图如图1所示。从图1中可以看出,转子在xOy平面旋转,将z轴旋转90°放平时,其旋转中心O1点的坐标为(x2,y2),转子重心点G的坐标为(xG,yG);转子质量偏心e0=O1G,振动偏心e=OO1;ω为转子旋转角频率。静止情况下定子和转子的形心重合,发电机运行过程中受到不平衡离心力、电磁力和电磁转矩等共同作用。

(a)系统动力学模型 (b) 转子坐标系
图1发电机转子-轴承系统示意图
Fig.1Schematicdiagramoftherotor-bearingsystemofgenerator
发电机两端采用导轴承支承,通常轴承油膜力可由轴颈位移及速度组合表示,当轴颈发生较小扰动时,认为轴承刚度和阻尼不变,设轴颈在x、y轴方向的位移分别为x1、y1,则x、y轴方向上的油膜力fx、fy分别为:
(1)
式中:kxx、kyy、kxy、kyx为导轴承的刚度系数,其中kxx=kyy,kxy=kyx;cxx、cyy、cxy、cyx为导轴承的阻尼系数,其中cxx=cyy,cxy=cyx。
考虑电磁刚度的发电机转子系统弯扭耦合振动微分方程组为:
(2)

为方便计算,引入无纲量变化:
Xi=xi/d,Yi=yi/d,(i=1,2),τ=ωt
其中d为单位长度,Xi、Yi分别为轴颈和转子的无量纲位移,τ为无量纲时间。
1.2 匝间短路时转子的弯曲及扭转电磁刚度计算
常采用能量法计算作用于发电机转子的不平衡电磁拉力和电磁转矩,当发生匝间短路故障时,发电机气隙磁场能量发生变化,进而作用力也会发生改变。不平衡电磁拉力是一种变载荷,不仅与转子的弯曲及扭转响应相互耦合,而且大小和方向也是随时变化的,与转子的运动位置及状态相关联。将不平衡电磁拉力和电磁转矩考虑成弯曲电磁刚度和扭转电磁刚度的形式,既可避开与转子弯曲及扭转响应相关的一系列复杂计算,又可解决激励作用方向随转子运动而随时变化等问题,是一种简单方便的处理方式。
1.2.1 气隙磁导分析


图2 发电机转子的气隙偏心示意图
Fig.2Schematicdiagramofairgapeccentricityofrotorofgenerator
发电机定转子的径向气隙长度δ(α,t)为:
δ(α,t)=δ0-ecos(α-β)
(3)
式中:δ0为均匀气隙大小。
偏心下的单位面积气隙磁导Λ(α,t)表达式为:
(4)
式中:ku为磁饱和度,ε为有效相对偏心,其中ε=e/kuδ0,Λ0为发电机均匀气隙磁导,n为泰勒级数展开阶数,μ0为空气磁导系数。
采用棣美弗定理,将气隙磁导经一系列计算变化后化为下式:
(5)
由式(5)可知,气隙磁导各分量中n=0的分量最大,n≠0的各项分量是由气隙偏心引起的,由于ε远小于1,随着n值的增大,气隙偏心引起的分量越小,故取气隙磁导的前三项即可满足计算精度要求,则单位面积气隙磁导经变换后为:
(6)

1.2.2 气隙磁场分析
正常运行时,发电机定转子合成气隙磁势与转子同步旋转[14],则合成气隙磁势f(α,t)为:
f(α,t)=Fscos(ωt-pα)+

(7)
式中:p为极对数,θ为内功率角,Fs、Fr分别为定子、转子绕组产生的基波磁势。
定子绕组匝间短路示意图如图3所示。当定子绕组发生匝间短路故障时,发电机失去对称性会产生短路电流,短路电流会引起一个围绕短路轴线波动的脉振磁场,忽略高次谐波磁势,则短路磁势表示fd(α,t)为:
fd(α,t)=Fdcos(ωt)cos(pα)
=Fd+cos(ωt-pα)+Fd-cos(ωt+pα)
(8)
式中:Fd为短路电流引起的磁势幅值,Fd+为与转子同相旋转的磁势幅值,Fd-为与转子反向旋转的磁势幅值。

图3 定子绕组匝间短路示意图
Fig.3Schematicdiagramofinter-turnshortcircuitofthestatorwindings
由式(8)可知,该脉振磁势由与转子同方向旋转的磁势和与转子反方向旋转的磁势两部分组成,第一部分不在转子绕组中产生额外的感应电势,第二部分会在转子绕组中感应出频率为电频率二倍的附加方向谐波电势,故转子励磁绕组电流中除了有短路前比较稳定的直流分量If0外,还有短路脉振磁场产生的2倍频交流分量If2,则励磁电流If(t)为:
If(t)=If0+If2cos2ωt
(9)
转子绕组中励磁电流产生的气隙主磁密分布B(t)为:
B(t)=(If0+If2cos2ωt)NΛ
=B0+B2cos2ωt
(10)
式中:N为转子每极励磁绕组匝数,B0=If0NΛ,B2=If2NΛ。
定子三相绕组感应电动势有效值E(t)为:
E(t)=2qfwkw1Blτ=KB
(11)
式中:q为每极每相槽数,f为电频率,w为单个线圈匝数,kw1为基波绕组系数,l为气隙长度,τ为极距,且K=2qfwkw1lτ。
三相绕组中的感应电势为:
(12)
由式(12)可知,三相绕组感应电势均由三个子项相加构成,第一项将形成以基频转速正向旋转的电枢反应磁势,第二项将形成以基频转速反向旋转的电枢反应磁势,第三项将形成以三倍频转速正向旋转的电枢反应磁势。故而可将定子绕组匝间短路故障下气隙合成磁势f(α,t)近似表示为:
f(α,t)=Fs1+cos(ωt-pα)+Fs1-cos(ωt
+pα)+Fs3+cos(3ωt-pα)+
Fr1+cos(ωt-pα+ψ+π/2)+
Fr1-cos(ωt+pα-ψ-π/2)+
Fr3+cos(3ωt-pα+ψ+π/2)
(13)
式中:Fs1+、Fs1-、Fs3+为电枢反应磁势幅值,且Fs3+=Fs1-;Fr1+、Fr1-、Fr3+为励磁电流产生的磁势幅值,且Fr1+=NIf0,Fr3+=Fr1-;ψ=θ+φ。
引入定子匝间短路程度表征参数v[15],各磁势幅值之间的关系为:
(14)
由式(14)可知,随v值的增大,气隙合成磁势中由短路所引起的反向旋转磁势幅值和三倍频旋转磁势幅值会增大。
1.2.3 短路时转子的弯曲及扭转电磁刚度计算
由电机学可知,发电机的气隙磁场能W为:
(15)
式中:Rg为转子半径,L′为转子有效长度。
将式(15)中气隙磁场能对转子振动位移求偏导数,得到X、Y方向上的电磁拉力分别为:
(16)
再将式(6)、(13)带入式(16)中,可得到匝间短路时作用于发电机转子上的不平衡电磁拉力,并且运用X=ecosβ=ecosωt,Y=esinβ=esinωt对其进行化简,整理后可得:
λ3+λ19+λ20+λ12+2λ7+λ8)cosωt+
(λ2/2+λ7+2λ8+λ12+λ19+λ20+λ21)·
cos3ωt-λ19cos(ωt-2ψ)-(λ4/2+λ21)·
cos(ωt+2ψ)-λ20cos(3ωt+2ψ)-(λ5/2)·
cos(3ωt-2ψ)+(λ3/2+λ12+λ21)·
cos5ωt-(λ6/2)cos(5ωt+2ψ)-(λ15+
λ18)sin(5ωt+ψ)-λ17sin(5ωt-ψ)-(2λ9
+λ13+λ14+λ11+λ17+λ15+λ18)sin(ωt+ψ)
-(λ9+λ13+2λ10+λ16+λ14+λ18)sin(ωt-ψ)
-(λ13+λ16+2λ11+λ15)sin(3ωt+ψ)-(λ10+
λ16+λ14+λ17)sin(3ωt-ψ)]
(17)
λ3-λ19-λ20-2λ7-λ8+λ12)sinωt+
(-λ2/2+λ19+λ20+λ7+2λ8-λ12-λ21)·
sin3ωt-λ19sin(ωt-2ψ)-(λ4/2+λ21)·
sin(ωt+2ψ)-λ20sin(3ωt+2ψ)-(λ5/2)·
sin(3ωt-2ψ)+(λ3/2+λ12+λ21)sin5ωt
-(λ6/2)sin(5ωt+2ψ)+(λ15+λ18)·
cos(5ωt+ψ)-λ17cos(5ωt-ψ)+(2λ9-λ13
+λ14-λ11+λ17+λ15+λ18)cos(ωt+ψ)+
(-λ9+λ13+2λ10+λ16-λ14-λ18)·
cos(ωt-ψ)+(λ13+λ16+λ11-λ15)·
cos(3ωt+ψ)+(-λ10-λ16+λ14+λ17)·
cos(3ωt-ψ)]
(18)
式(17)~式(18)中各参数变换如下:
λ8=Fs1+Fs3+,λ9=Fs1+Fr1+,
λ10=Fs1+Fr1-,λ11=Fs1+Fr3+,λ12=Fs1-Fs3+,
λ13=Fs1-Fr1+,λ14=Fs1-Fr1-,λ15=Fs1-Fr3+,
λ16=Fs3+Fr1+,λ17=Fs3+Fr1-,λ18=Fs3+Fr3+,
λ19=Fr1+Fr1-,λ20=Fr1+Fr3+,λ21=Fr1-Fr3+。

cosθ+(λ13+λ11)cos(θ+2ωt)+(λ10+λ16)·
cos(θ-2ωt)+λ17cos(θ-4ωt)+λ15·
cos(θ+4ωt)]+[(λ9+λ14+λ18)sinθ+(λ13+
λ11)sin(θ+2ωt)+λ17sin(θ-4ωt)+(λ10+
λ16)sin(θ-2ωt)+λ15sin(θ+4ωt)](-φ)}
(19)
分析不平衡电磁拉力表达式(17)、(18)可知,定子绕组匝间短路主要引起频率为1倍频、3倍频、5倍频的奇数次倍频径向振动;通过比较各项系数可知,1倍频的系数要比3倍频和5倍频的系数大,所以匝间短路故障主要引起1倍频的振动,其次是影响3倍频的振动。由电磁转矩的表达式(19)可知,定子匝间短路故障主要引起2倍频、4倍频的偶数次倍频扭转振动;各项系数中2倍频系数受短路参数影响最大,故匝间短路故障时发电机转子扭转振动的2倍频振动量变化最为显著。
将式(16)和式(19)分别取位移一次项系数可得发电机的弯曲电磁刚度Fex、扭转电磁刚度Fey、电磁转矩Me分别为:
(20)
其中:
2 数值算例与分析
采用变步长四五阶Runge-Kutta法对系统运动微分方程进行积分,积分步长为T/360。系统相关参数为:m1=2 kg,m2=30 kg,Ip=0.201 kg·m2,kw=5.2×105N/m,抗扭刚度kt=2.53×106N·m/rad,弯曲阻尼比为0.02,扭转阻尼比为0.05,kxx=4.88×106N/m,cxx=3.1×106N·s/m,e0=0.5 mm,额定转速为3000 r/min,额定功率为10 kW,δ0=0.8 mm,μ0=4π×10-7H/m,p=1,Rg=0.24 m,L′=0.3 m,Fr=101.6 A,Fs=1050 A。
2.1 发电机转子弯曲及扭转振动时域分析
图4为发电机转子水平方向的位移时域图。从图4中可以看出,随着定子发生匝间短路故障程度的加大,转子的弯振幅值波动范围逐渐增加,幅值由2.3 mm增加到3.5 mm,转子振动加强。

(a)正常 (b)短路1%

(c)短路5% (d)短路10%
图4转子水平方向位移时域图
Fig.4Timedomaindiagramoftherotorhorizontaldisplacement
图5为发电机转子扭转振动角位移时域图。从图5中可以看出,正常运行时,发电机电磁转矩受直流分量的影响,不具备振动特性,受转矩脉动激振力的影响,转子扭转振动幅值几乎不变,而定子发生匝间短路后,由于发电机电磁转矩激振力成分增加,转子的扭振幅值也增加,且随短路程度的增加幅值波动范围逐渐增大,扭转振动波形也由正弦波形变为畸变的波形。

(a)正常 (b)短路1%

(c)短路5% (d)短路10%
图5转子扭转振动角位移时域图
Fig.5Timedomaindiagramoftherotortorsionalvibrationangulardisplacement
2.2 发电机转子弯曲振动频域分析
图6为发电机转子水平方向振动频谱图,表1为各频率下转子水平方向的振动速度。从图6中可以看出,在发电机正常运行状态下,其速度振动频率主要是1倍频成分(转频为50 Hz),而发生定子匝间短路故障后,除了使1倍频振动增加外,还会引起3倍频和5倍频等奇数次倍频成分的明显变化,且随故障程度的增加,3倍频和5倍频等成分幅值会增大。从表1中可以看出,与正常运行状态相比较,定子匝间短路1%、5%、10%时,转子1倍频振动分别增加了2.3%、13%、32%,且各频率的振动量中1倍频的振动最大。以上仿真结果与定子匝间短路时发电机转子不平衡电磁拉力的理论分析相吻合,也与文献[16]中通过实验验证的理论结果相符合。

(a)正常 (b)短路1%

(c)短路5% (d)短路10%
图6转子水平方向振动频谱图
Fig.6Frequencyspectraoftherotorhorizontaldirectionvibration

表1 转子水平方向振动速度
2.3 发电机转子扭转振动频域分析
图7为发电机转子扭转振动频谱图,表2为各频率下转子扭转振动角位移。从图7中可以看出,发电机正常运行时电磁转矩为常值,扭转振动以0倍频为主,而发生定子匝间短路故障后,除了使扭转振动0倍频成分增加外,还会使2倍频和4倍频等偶数次倍频成分增加,且随故障程度的增加,2倍频和4倍频等成分幅值会增大。从表2中可以看出,随匝间短路故障程度的加大,转子扭转振动各频率中2倍频振动量的增长速度最快。以上仿真结果与定子匝间短路时发电机转子电磁转矩的理论分析相吻合,也与文献[17]中通过实验验证的理论结果相符合。
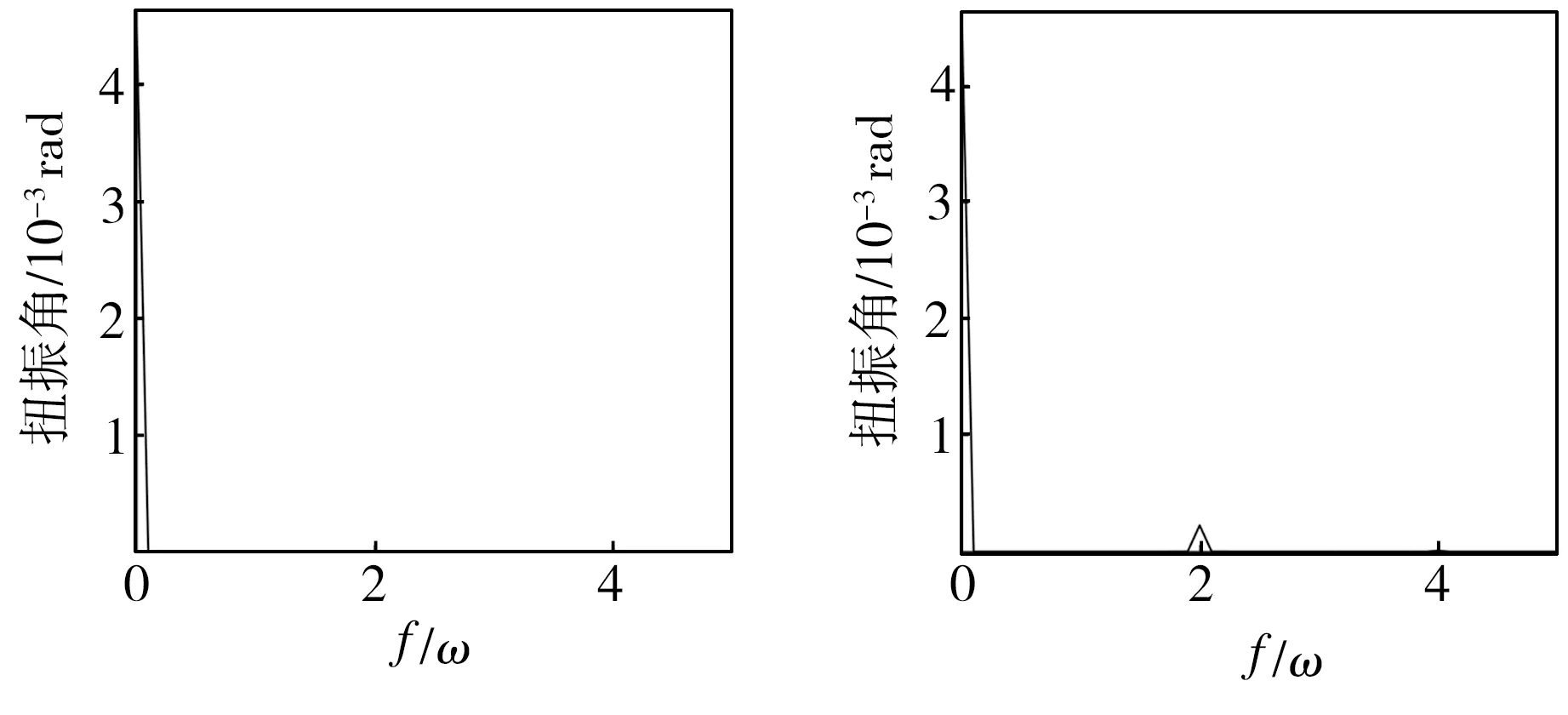
(a)正常 (b)短路1%

(c)短路5% (d)短路10%

图7 转子扭转振动频谱图
3 结论
(1)发电机定子绕组匝间短路故障不仅会使转子的弯曲振动和扭转振动幅值增加,而且还会引起转子弯曲振动和扭转振动中倍频及高倍频振动量的增加。
(2) 定子绕组匝间短路故障发生后,转子的弯振变化特征与其所受电磁拉力变化相似,1、3、5等奇数次倍频振动量增加;转子的扭振变化特征与电磁转矩变化相似,2、4等偶数次倍频振动量增加;随短路程度的增加,弯振中1倍频振动量最大,扭振中2倍频振动量变化最为显著。

