消费偏好参数估计中协整模型的选择
张 磊,喻崇武,虞 洪,张 霞
(1.四川省社会科学院,成都 610072;2.北京第二外国语学院 国际商学院,北京 102488)
0 引言
消费和偏好对于任一经济体或经济理论都极为重要。随着收入和利率的变化,消费者会面临期内不同商品间(期内替代)和相同商品不同时期(跨期替代)两种权衡选择。研究这两种关系有助于理解消费者的消费结构(如恩格尔曲线、政府支出效益等)和货币政策的影响(如跨期替代弹性等)。消费偏好参数也是很多重要经济模型(如C-CAPM模型、增长模型等)的基本要素以及估计支出弹性和价格弹性等常用变量的必要条件。因此,准确估计偏好参数具有重要的理论和现实意义。
现代经验文献一般在理性预期的生命周期理论框架下[1],采用协整方法对最优化一阶条件估计偏好参数。协整方法有两方面的优势。一方面,协整估计并不要求结构变量都是外生的,这对很多变量内生的动态随机模型十分重要。另一方面,它对测量误差、偏好冲击、流动性约束以及消费者异质性等干扰因素具有更好的包容性[2]。只要每种商品的测量误差和偏好冲击平稳,则估计结果是一致的。当每个消费者偏好参数相同且平均消费对数和消费量对数均值间的差异是平稳的,那么加总过程也不会带来任何不利影响。只要消费者最优化过程存在内解,那么面临流动性约束时估计结果仍然稳健。因此,协整方法被广泛地用于各种偏好参数估计[3-6]。但由于实际问题和模型的限制,以往研究依然存在三方面的缺陷。一是由于时间序列变量可能有多种线性组合存在协整关系,使得方程选择未必正确。二是数据本身的复杂性,使得事先假定个别偏好或商品性质并据此估计模型的方法有过度挖掘数据的嫌疑。三是大多数研究受限于两种商品的效用函数,不同类商品加总过程可能抵消商品和偏好的真实性质,使得估计有偏。
鉴于以上三个问题,本文结合以往研究对协整方法进行了三个方面的扩展:(1)引入多种商品和服务的Addilog效用函数,以减少两种商品时线性加总对商品和偏好性质的掩盖;(2)考虑了消费对时间不可分的情形,使得模型同时兼容于习惯形成效应和耐用品消费;(3)考虑了非平稳的偏好冲击和确定趋势的技术进步冲击,使得模型在长期时间序列数据中更具有适用性。在此基础上,讨论了当面临多个协整关系时模型的选择方法和依据,并总结了分析此类实证问题的一般思路。
1 时间不可分、习惯形成与耐用品
假定消费者在给定劳动收入、商品价格以及资产收益率路径外生的前提下,通过选择消费和投资路径进行终身效用最大化。即期效用函数采用Addilog形式[7]。那么消费者最优化问题为:

其中Et(·)表示基于t期可获得信息的条件期望,β∈(0,1)为主观折现因子。假定有n 种商品,Pi(t)和 Ci(t)分别为t期第i种商品价格和实际购买量。I(t)和A (t)分别表示消费者第t期劳动收入和资产存量,A0为初始资产存量,R (t)为资产净收益率。t仅起时间标识作用。Si(t)为消费服务流,当Si(t)=Ci(t)时,效用对时间可分,仅取决于当期消费。γi表示第i种商品消费的跨期替代弹性或者曲率参数。
效用对时间不可分主要缘于习惯形成效应和商品耐用性质。为了简便,本文采用Dynan[8]的方法模拟习惯形成与耐用品消费,消费服务流 Si(t)=Ci(t)-hiCi(t-1)。参数hi∈(-1,1)是衡量消费习惯形成效应和商品耐用程度的参数。如果为正,说明习惯形成因素占主导,消费者上期消费越多当期需要消费就越多,以维持同样的效用水平;如果为负,说明商品耐用性占主导,前期购买在当期仍然产生效用;如果为零,则说明该商品既不明显具有习惯形成效应也不是耐用品或者二者作用抵消[9]。
此时最优化问题的Lagrange函数为:
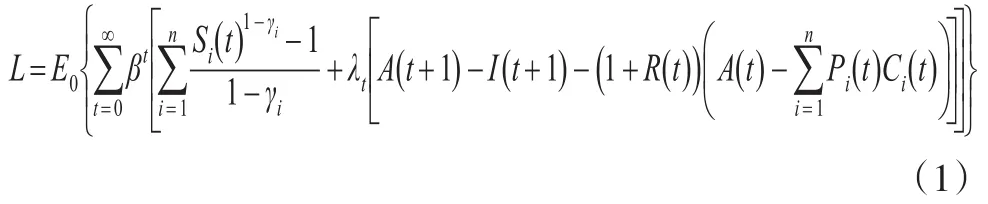
设定第1种商品为计价商品,价格标准化为1。假定存在内解,则最优化一阶条件为:

将Si(t)表达式带入,两边同时取对数,整理可得:

其中:

j=1,2,...,n,Mj和 Nj中约等号右边分别由对和作一阶泰勒展开及得来。代入式(3)整理可得:

其中:

依据 Muellbauer[10]、Croix[11]等的研究,如果 lnCi(t)、lnC1(t)和 lnPi(t)都是 I(1)过程,那么式(4)意味着一个平稳的协整关系,因为该式右边部分全是协方差平稳变量,即:

如果式(4)右边均值为零,则式(5)对应的回归方程为:

其中 εi(t)是误差项,均值为零。
因此,回归方程(6)中常数项是否显著存在以及符号正负,取决于两种商品的习惯形成效应和商品耐用性质差异。如果两种商品或服务在这两方面没有显著差异,则回归方程常数项不显著地异于零;若第i种商品消费体现出显著的习惯形成效应而第1种商品是耐用品,在以往一般经验 β→1和 γj接近为零的条件下,常数项应当显著为负;反之,则常数项显著为正。但是在效用对时间严格可分的特例中,hj=0,nj=1,...,n,式(6)中常数项为零,回归方程不应当存在常数项。
2 偏好冲击与技术进步
根据主流经济增长和结构变化理论[12],长期中均衡变化的原因主要在于需求和生产效率的变化。即消费者偏好和不同行业遭受技术冲击决定了市场出清中的均衡。实际中获取的消费数据也由这两个因素决定,因此测量长期偏好参数必须考虑这两方面干扰的影响。
传统宏观模型处理技术冲击的一般做法是引入确定性时间趋势的技术进步率。微观数据加总模型也常常如此,Amano和Wirjanto采用确定性趋势项抓取商品质量改进过程。根据以往研究,假定供给冲击随时间呈确定性趋势变化,引入对数趋势平稳的技术冲击ecit+vit。其中ci表示技术进步率中的趋势性部分,其值由行业特征外生决定,若ci>0,说明长期中第i种商品生产技术水平随时间递增;反之,技术水平随时间下降。对于两种商品和服务,若ci>cj,说明第i种商品和服务的生产技术进步比第j种商品和服务快。vit~WN(0,δ2)是一个白噪声过程,表示其他因素对技术进步的随机干扰。

同时代入φi(t)和 Si(t)的表达式,再两边取对数,整理可得:

相对于上文,Mj的表达式变为:

而Nj的表达式保持不变。进一步整理,式(8)变为:

其中:
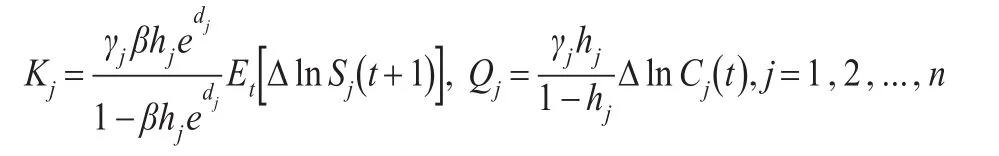
由于dj是常数,因此式(9)仍然意味着一个平稳的协整关系:

在上文对Kj和Qj的假定下,式(10)对应的协整回归方程可以表示为:

其中εi(t)是误差项,均值为零。
如果不考虑习惯形成和耐用品消费,hj=0,j=1,...,n,那么常数项仅取决于固定偏好倾向差异ai-a1。如果相对于计价商品消费者对某种商品和服务存在显著的固定偏好倾向,则方程应该有常数项;反之,常数项可能并不显著地异于零。确定性时间趋势项则取决于偏好冲击和技术变化的综合效应,如果两种商品和服务的综合效应差别显著,那么方程时间趋势项应当显著异于零。但这里更深一层含义是,如果相对于另一种商品或服务,某种商品或服务技术改善明显但并不比其更受消费者欢迎,那么趋势项也可能不显著地异于零。类似的,如果不能排除习惯形成效应和耐用品消费的影响时,常数项是否显著存在也是取决于这些干扰的综合差异,而并非其中个别冲击或多种冲击本身。
3 实践中的模型选择
通过上文的例子,不难发现回归方程的形式实际上取决于干扰类别和方程中所涉两种商品或服务遭受干扰的差异。但以往大多数文献并未意识到这一点,构建和选择回归方程时都只考虑干扰本身,而不是方程中涉及到的两种商品或服务遭受干扰的差别。
在实践中,应当首先明确对象遭受干扰的主要类型并据此比较商品间的差异。比如对于中国的消费均衡,黄桂田和赵留彦[14]发现供给冲击比需求面的影响更大,而任若恩和孙琳琳[15]发现服装及其他纤维制品制造业、木材业和家具业TFP增长率明显高于食品制造加工及饮料制造行业。因此,如果其他干扰不足够重要,那么食品类商品和服务与这几类商品和服务构成的方程应当存在显著异于零的时间趋势项。Browning和Collado[16]发现西班牙居民食品消费中外出就餐和烟酒消费具有习惯形成性质,但是衣着类和家庭小型耐用品具有耐用性质。如果偏好倾向及其他干扰并不具有相当的影响,那么外出就餐和烟酒消费与衣着类和家庭小型耐用品构建的协整方程应当存在显著异于零的常数项。
明确主要干扰后,依据商品和冲击性质进行合理分类也是非常必要的。依据Ogaki和Reinhart[17]的研究,在估计加总商品的偏好参数时,如果将耐用品当作非耐用品处理,将导致估计结果偏小甚至为负,但将非耐用品当作耐用品处理则几乎没有影响。Ogaki[18]没有考虑商品耐用性,在估计一类商品跨期替代弹性时直接将其他所有商品线性加总,掩盖了商品和偏好的真实性质,最终几组数据的参数估计结果均趋近于零。
除了运用前文阐述的方法选择回归模型外,还可以通过不同方法估计方程进行对比,以确保稳健性和可靠性。目前估计协整关系的方法主要有完全修正普通最小二乘法(FMOLS)、动态普通最小二乘法(DOLS)以及正交协整回归法(CCR)。但根据Stock和Watson[19]、Cappuccio和Lubian[20]以及Christou和Pitts[21]等的研究,这些估计方法在扰动项自相关、扰动项与解释变量相关或样本量受限时,均存在不同程度的均方根误差和二阶偏差。甚至依据Kejriwal和Perron[22]的研究,小样本时DOLS方法估计中领先项和滞后项都不易于确定。进一步地,即便这些偏差可以接受,但若一组变量存在多个协整关系时,这些估计方法仍然无助于方程的识别和选择。
4 结论性评述
本文在理性预期的生命周期理论框架和多商品Ad-dilog效用函数下,分别以习惯形成效应、耐用品消费、非平稳偏好冲击和技术冲击为例,系统地阐述了将协整方法应用于偏好参数估计时回归方程选择的问题。本文认为,方程是否存在常数项和时间趋势项应当取决于主要干扰在两种商品和服务间的差异而不是这些干扰本身。在建立协整模型和选择回归方程时,应当结合实际识别占主导的干扰类型以及其在不同商品和服务间的差异,并对商品和服务进行合理分类,以免盲目加总造成偏差。
协整方法在估计偏好参数时具有很多优越性,以往研究已经将其广泛应用于居民消费偏好测度、政府支出与私人消费之间的替代、国际贸易等领域。在数据上也从时间序列数据扩展到面板数据。经过本文对干扰的扩展和方法的规范,可以将协整方法进一步推广到多种商品但性质或遭受干扰并不统一的情况,以及给定主要干扰性质后,相关参数的进一步估计,并且使协整方程的选择更加合理,估计结果更加稳健。
尽管如此,协整方法还是存在一些缺陷。比如采用多种商品的效用函数时,由于基准组的参数将会出现多个估计值。如何在这些值之间进行取舍或者加权,需要更进一步的讨论。以往大多数研究倾向于利用协整方法与GMM法的估计结果进行比较,但是GMM法估计标准欧拉方程的基本假设是变量间存在确定性关系。这使得二者估计结果不一致,很难达到比较效果。
——从耐用品与非耐用品消费的视角

