联合信道非相干网络编码调制方法

高枫越,王 琰,李 牧,于 睿

(1.陆军工程大学 通信工程学院,南京 210007; 2.军事科学院 系统工程研究院,北京 100141)(*通信作者电子邮箱bettina211@163.com)

0 引言

网络编码(Network Coding, NC)[1-4]能够改善多用户无线网络的吞吐量和可靠性。对于双向中继网络(Two-Way Relay Network, TWRN),由于物理层网络编码(Physical-layer Network Coding, PNC)允许两个终端节点同时向中继节点传输信息,使得频谱效率翻倍。这种去噪转发(DeNoise and Forward, DNF)协议[5]的方式相对于其他转发协议有更好的性能,它是一种从无线信道的复数域到有限域的一种多对一的映射技术。对于DNF协议,大多数文献都是基于相干检测方式的研究,即假设中继节点已知所有链路的信道状态信息(Channel State Information, CSI)[6-7]。然而,相干接收机面临许多实际的挑战,需要大量的计算开销和高速的采样率来估计CSI。相比之下,非相干的双向中继系统实现复杂度更低,但其抗噪声性能也更差。为了解决这个问题,多天线的双向中继系统可以通过实现额外的分集增益来提高误比特率(Bit Error Rate, BER)性能。空间调制(Spatial Modulation, SM)技术作为一种新的多输入多输出(Multiple-Input Multiple-Output, MIMO)技术,相对于传统MIMO技术在能量、BER性能及硬件复杂度上都更有优势[8-10]。文献[11]考虑了有限字符输入系统的无线物理层安全传输问题,提出了一种SM安全传输方法。文献[12]推导了SM系统的BER上界,并通过合理配置天线数量和调制阶数,优化SM系统BER性能。差分空间调制(Differential Spatial Modulation, DSM)可以避免对信道信息的依赖,同时具有SM技术的全部优点,已经应用于点对点的传输系统[13-16]和两跳的中继传输系统中[17-18]。

由于PNC本身的差错控制能力有限,往往与信道编码结合,或称为联合译码的物理层网络编码(Joint Channel decoding and physical-layer Network Coding, JCNC),保证在提高吞吐量的同时,提高信息的可靠性。文献[19]针对差分编码的AF和DNF的双向中继系统提出了非相干的ML检测方法。文献[20]基于二进制频移键控(Frequency Shift Keying, FSK)的PNC设计了联合Turbo码的非相干接收机。

比特交织编码调制(Bit-Interleaved Coded Modulation, BICM)是一种联合二进制信道编码与多进制调制的技术,码字经过比特交织、调制,送入信道,接收机进行解调、解交织、软信息译码,得到每个比特的软信息。正是这种比特交织的方式,避免了突发错,使得BICM有很好的抗衰落性能,通过信道译码器到解调器的信息反馈和迭代检测可以改善BICM的能量效率,这种从译码器到解调器的反馈称为比特交织编码调制迭代译码(BICM with Iterative Decoding, BICM-ID)[21]。关于BICM-ID,文献[22]设计了点对点的FSK调制的接收机,文献[23]将其进一步扩展到双向中继系统中,给出PNC方案的中继非相干接收机设计思路。文献[24]则考虑了模拟网络编码(Analog Network Coding, ANC)方案下端节点非相干接收机的设计方案。

综上所述,关于BICM-ID系统中的非相干PNC接收机的研究还比较少,本文基于BICM-ID系统,提出了一种基于差分空间调制的PNC接收机设计方案。在没有CSI的情况下,中继接收机能够采用非相干解调的方式得到网络编码比特的对数似然比(Likelihood Ratio, LLR),经译码器进行软译码,再通过迭代反馈的方式进一步改善系统的抗噪声性能。同时计算机仿真结果验证了本文方案能够实现可靠的PNC非相干接收。

1 系统模型

多天线下双向中继协同传输模型如图1所示,系统由2个源节点(A和B)和1个中继节点(R)组成。两个源节点通过中继节点进行信息交换,假设由于距离、障碍物等因素影响,两个源节点之间没有直达链路。两个源节点各配备Nt根天线,中继节点配备Nr根天线,系统采用半双工的通信方式,即在某一时刻节点只能进行发送或者接收。在k时刻,从源节点到中继节点的信道分别用Nt×Nr的矩阵HA[k]和HB[k]表示。这里假设信道都服从相关的瑞利平坦衰落模型,信道矩阵Hi[k]的每个元素都是均值为0、方差为1的复高斯随机变量,即信道Hi[k]∈CNt×Nr(i=A,B)。假设衰落具有准静态特性,衰落过程足够慢,即假设信道参数Hi在两个连续的矩阵传输间隔内保持不变。因此,对所有k值,有Hi[k]≈Hi[k-1]。同时考虑到信道的时变衰落特性,信道参数之间的时间相关性服从最大的归一化多普勒频率为fD的Jakes模型。

图1 双向中继系统模型Fig. 1 Two-way relay system model

2 发射机传输方案

1)每个子时隙只有一根天线能够发送信号,也就是说,空间调制矩阵的每一列中只有一个非零元素;

2)在一个空间调制矩阵的传输期间,每根天线在Nt个连续的子时隙中仅有一次能够发送信号,也就是说,空间调制矩阵的每一行中只有一个非零元素;

3)信号的星座图是等能量的M-PSK(M-ary Phase-Shift-Keying)调制符号集Ψ={exp(j2πm/M)|m=0,1,…,M-1},也就是说,矩阵的每个元素都属于符号集合Ψ。

举个例子说明,在二进制相移键控(Binary Phase Shift Keying, BPSK)调制方式下,当源节点天线数Nt=2时,可以将两个二进制比特映射为一个2×2的空间调制矩阵。第一个比特表示发送的BPSK符号携带的信息是1还是0;第二个比特表示天线的发送顺序是正序还是逆序,即空间调制矩阵还是反对角阵。映射方案总结在表1中。

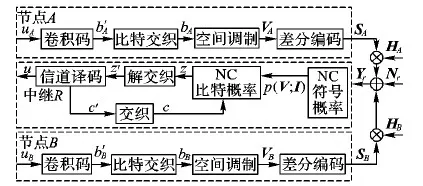
图2 发射机结构Fig. 2 Transmitter structure

表1 BPSK下源节点空间调制映射方案(Nt=2)Tab. 1 Source mapping for SM with BPSK and Nt=2

当Nt>2时,根据Nt是奇数还是偶数,分以下两种情况考虑:

1)当Nt=2L时,将2L个编码比特每两个比特分为一组,然后根据表2可以得到L个2×2的空间调制矩阵。接着将矩阵中的元素从内到外沿两条对角线扩展为2L×2L的空间调制矩阵,如图3(a)所示。

2)当Nt=2L+1时,首先将第一个比特映射为BPSK调制符号,放置在(2L+1)×(2L+1)的中心位置。其他2L个比特同样是每两个分为一组,得到L个2×2的空间调制矩阵,接着将矩阵中的元素从内到外沿矩阵(2L+1)×(2L+1)的两条对角线向四周扩展,最终得到(2L+1)×(2L+1)的空间调制矩阵,如图3(b)所示。

本文与点对点通信的空间调制矩阵不同。以Nt=2为例,在点对点通信中,两根发射天线携带的信息不同,每根天线上的调制符号均可携带1比特的信息。而本文在设计空间调制矩阵时,两根天线携带的信息相同,与点对点通信相比少传输了1比特的信息。这种设计主要是考虑到中继节点对叠加信号的处理能力有限,因此以牺牲一定的传输效率为代价,降低系统的复杂度。

图3 空间调制矩阵设计方案Fig. 3 Design scheme for SM matrix

在进行空间调制得到矩阵Vi后,将调制符号进行差分编码得到:

Si[k]=Si[k-1]Vi[k];Si[0]=INt

(1)

传输过程分为两个阶段:

在第一阶段,两个源节点分别将符号Si[k]同时发送给中继节点,为了简化分析,假设传输信号之间理想同步,则中继节点接收到的符号可以表示为:

Yr[k]=SA[k]HA[k]+SB[k]HB[k]+Nr[k]

(2)

其中:Nr[k]∈CNt×Nr是中继节点接收机处的白噪声信号。

在第二阶段,中继节点对接收到的叠加信号Yr[k]进行解调、解交织,然后进行信道译码,得到合并的网络编码比特信息序列u=uA⊕uB。得到网络编码比特序列以后,中继节点对比特信息序列u按照与源节点相同的处理方式,重新进行信道编码、比特交织和常规的差分空间调制,最后广播给两个源节点,两个源节点接收到的信号可以表示为:

Yi[k]=Hi[k]Sr[k]+Ni[k];i=A,B

(3)

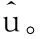
3 网络编码符号的联合概率密度函数

在k时刻,中继节点根据相邻两个时刻从源节点接收到的信号Yr[k-1]和Yr[k],联合检测网络编码信息符号。将中继节点相邻两个时刻接收的信号写成向量形式,结合时变衰落信道的准静态特性,即相邻两时刻的CSI近似不变,将式(2)进行整理得到:

(5)

其中：

(6)

令V[k]=VA[k]+VB[k],将式(5)的条件概率密度表达式经过展开得到:

((2+N0)2INt-VH[k]V[k])-1Yr[k-1]+

((2+N0)2INt-V[k]VH[k])-1Yr[k]))

(7)

进而,得到最大后验概率的表达式:

(8)

其中:Ω表示包含所有空间调制矩阵Vi[k]的集合。中继需要采用多对一的DNF映射Θ:Ω2→Ω以保证源节点能够正确译码。因此,映射必须满足排他准则[25],同时根据式(8),将网络编码符号概率转化为相应的比特概率,以BPSK调制下,源节点天线数Nt=2的映射方案为例,中继处叠加符号映射方案总结在表2中。

表2 BPSK下中继节点空间调制映射表(Nt=2)Tab. 2 Relay mapping for SM with BPSK and Nt=2

4 迭代译码算法

为了进一步改善误码性能,本章在之前推导出的PDF的基础上给出了迭代检测算法。基本思想是中继节点检测器解调接收信号,计算出两个源节点发送的联合符号的概率,通过符号概率进一步计算出发送的二进制网络编码比特的概率。将网络编码比特概率信息转化为对数似然比LLR作为信道译码器的先验信息,信道译码器通过软译码得到网络编码比特的外信息,反馈回检测器再次进行解调。经过几次迭代后,最后由译码器输出二进制网络编码信息比特序列。

下面详细介绍具体的迭代译码过程。在所有解调和译码的过程中,发送符号的概率是固定的,可以由式(7)计算得到,用p(V;I)来表示。将这里的V定义为由两个源节点信息符号VA和VB构成的联合符号,即:

V=(VA,VB);VA,VB∈Ψ;V∈Ψ2

(9)

中继节点需要针对每个联合符号计算概率p(V;I),由于集合Ψ2中元素的个数为|Ψ|2,中继节点需要进行|Ψ|2次计算。而传统的点对点传输仅需要进行|Ψ|次计算。

用p(b;I)来表示信道译码器反馈回来的二进制网络编码比特概率,将p(V;I)和p(b;I)作为检测器的输入。其中,b表示映射为联合符号V的q个二进制比特。p(b;I)={p(bk;I),0≤k≤q-1},bk=bk,A⨁bk,B,bk,i∈{0,1}表示映射为符号VA的第k个二进制比特。由于在第一次迭代检测时,没有译码器的反馈信息,假设比特概率p(b;I)相等。经过检测器解调后,得到经过估计的编码比特概率值p(b;O)={p(bk;O),0≤k≤q-1}。基于联合符号V的输入输出分布均用概率表示,而基于映射为联合符号V的网络编码比特的输入输出分布需要以LLR表示,同时LLR更便于软判决译码,因此,检测器输入的映射为符号V的第k个编码比特概率p(bk;I)的LLR可以表示为：

(10)

其中:p(bk=1;I)和p(bk=0;I)分别表示检测器输入的映射为符号V的第i个编码比特为1和为0的概率。检测器输出的映射为符号z的第k个比特概率p(bk;O)的LLR可以表示为：

(11)

其中:p(bk=1;O)和p(bk=0;O)分别表示检测器输出的映射为联合符号z的第k个编码比特为1和为0的概率。检测器输出比特概率与输入比特概率之间的关系可以表示为：

(12)

其中:{Ψ2|bk=l}代表联合符号所携带的第k个比特信息bk为l∈{0,1}的所有符号的集合。可以将式(12)改写为：

(13)

将式(13)代入式(11),得到

(14)

为了计算简便,采用max-star函数表示上面得到的结果,max-star函数的表达式为：

(15)

其中二元max-star函数可以展开为:

max*(x,y)=max(x,y)+ln(1+exp(-|x-y|))

(16)

三元以上max-star函数可以通过对二元函数进行递归的方式求出。

5 仿真结果

本文方案是针对DF的PNC,在该系统中,中继需要从两个源节点发送的叠加信号中检测出网络编码的比特信息,因此,系统的瓶颈在于中继节点的处理能力。在联合信道非相干PNC方案中,MAC阶段中继的任务是重构两个源节点比特信息的XOR,而在BC阶段中继重新进行调制编码后广播网络编码信息已经退化成点对点的通信过程,因此本文主要关心MAC阶段中继节点检测出的网络编码码字的抗噪声性能。

在本文的Monte Carlo仿真实验中,采用修改的Jakes模型模拟瑞利衰落信道,信道编码采用1/2码率的(7,5)卷积码,比特交织长度为2 000。假设两个源节点到中继的信道完全对称,两条信道的方差均为1。信道相关性由归一化多普勒频率决定,根据信道归一化多普勒频率大小,将信道分为两种情况:1)所有节点都是固定的或者慢速移动的,即所有信道都是慢衰落,fD=0.001;2)所有节点都是移动的,即所有的信道都是快衰落,fD=0.03。

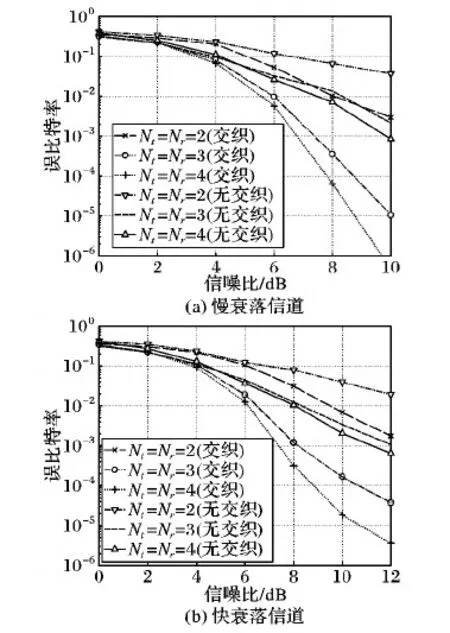
图4 BPSK调制不同天线数目中继节点处的BER性能Fig. 4 Simulation BER under different antenna numbers for DBPSK at relay

图4给出了基于BPSK调制方式,慢衰落fD=0.001信道和快衰落fD=0.03信道下相同频谱效率时不同传输天线数目的BER性能对比。从图4(a)可以看出,随着天线数目的增加,误码率下降速度也随之加快,这说明增加天线数能够提高系统的分集增益;同时,可以看出,增益越来越小。采用比特交织技术后,BER性能有所提升,在误码率为10-4情况下,Nt=Nr=4仅比Nt=Nr=3提高了1 dB左右。由于信道变化很慢,对BER的影响不明显,因此在慢衰落信道下可以有效地实现物理层网络编码的非相干传输。从图4(b)中同样能够看出,增加天线数可以提高系统的分集增益。由于节点移动速度加快,多普勒频率更大,信道的时间相关性更低,由节点移动性带来的干扰对系统BER产生了影响,在误码率为10-4情况下,Nt=Nr=4比Nt=Nr=3提高了1.5 dB左右。当Nt=Nr=4时,误码率曲线的斜率随着信噪比增加变得缓慢,说明本文对信道近似不变的假设而引入的干扰已经超过噪声,成为影响系统抗噪声性能的主要因素。对比图4(a)和(b),也可以看到相同传输天线数目的条件下,快衰落信道下系统的BER更高,抗噪声性能更差。

6 结语

本文针对双向中继信道下的差分物理层网络编码问题,提出了多天线场景下的联合信道-非相干物理层网络编码调制和检测方法。推导得到了中继节点处的最大后验概率检测表达式,利用信道编码的线形结构,结合比特交织、信道译码与软入软出检测算法,进而得到联合信道-差分物理层网络编码迭代检测方法。仿真结果表明,提出的方法能在双向中继场景下实现物理层网络编码的非相干传输与检测,有效提高了系统的吞吐量和频谱效率。下一步,将考虑差分正交空间调制与物理层网络编码的结合问题。