手臂抓取时空协调神经网络模型构建方法研究

张少白，施梦甜

(南京邮电大学 计算机学院，江苏 南京 210023)

0 引 言

近年来，行为和认知神经科学迅速发展，不仅深化了人类对大脑行为功能机制的理解，而且推动了其与神经计算科学的结合，有力地促进了机器智能的发展。神经解剖学、神经生物学的研究成果为阐明人类认知机理提供了大量的实验证据和理论观点，如何利用这些研究发现构建新的认知计算模型，将其应用于3D手势跟踪人机交互，是目前许多学者研究的重点，其中包括了手臂运动协调控制模型。

Jeannerod针对手臂抓取运动提出的概念模型指出，抓取运动由延伸(运动)和抓取(操作)组件构成，两个组件具有独立的视觉运动通道，并由一个统一的中心时间机制进行协调[1]。针对手臂运动形式和手部预成型之间有关的时间协调问题，Hoff和Arbib通过剩余时间(time-to-go)预估的形式构建了一个基于最小加加速度(minimum jerk)最优标准的控制模型[2]，解释了手臂运动以及手部预成型相关过程的运动学原理，但未考虑组件间的空间协调，线性确定最大抓取孔径(maximum grip aperture，MGA)的方式不能准确反映实验结果。Haggard和Wing指出手部抓握形状很大程度上取决于手臂移动的空间位置，并构建了一种在线误差轨迹驱动纠正模型用于实现组件间的空间状态交流[3]。后来，基于Bullock的VITE(vector integration to endpoint)手臂运动轨迹生成模型[4]，Ulloa提出了一种通过不断更新向量位置命令以实现运动协调的神经网络模型[5]。Vilaplana等利用最大抓取孔径更新变换和中心协调函数统一控制的方法实现了抓取延伸组件的时空协调[6]，但模型需要人为设定MGA，对实验的真实性具有不确定影响因素。文献[7-8]在手臂抓取的时间和空间维度分别提出了一种轨迹优化算法。文献[9]利用小脑超前状态学习和剩余时间预测构建了一种运动协调控制模型。鉴于此，文中期望构建一种无需人为干预的、能自动调节抓取孔径再现抓握过程的时空协调神经网络模型。

手臂抓取运动要求各组件能协调、同步和变速，既需要不同肌群之间具有较好的协同性，且在抓取过程中速度是可以被改变的[10]。VITE模型较好地满足了以上特性，其门控(GO)信号与大脑基底神经节(basal ganglia)的作用基本相符。文献[10-11]指出基底神经节具有相当多类型的认知调节作用，不仅协调运动、锥体系功能，支持条件反射、空间知觉、注意转换等简单的认知和记忆功能，而且参与启动效应、言语记忆、逻辑推理等复杂的认知和记忆功能。

基于此，文中借鉴Bullock VITE模型的构建理念，在利用基底神经节对手臂抓取运动进行时间协调的基础上，设置组件间状态信息交流的耦合单元用以实现空间协调，并且针对目标物体距离、位置变化等实验扰动情况，增设了本体感受和目标物体内部表示差异的监督细胞，构建了一个具有神经生物学意义和较好认知功能的时空协调抓取模型。不同于Vilaplana模型，该模型无需人为指定最大抓取孔径，采用运动速度自动调节抓取孔径的方式能更好地生成最大抓取孔径并指导手势合拢，避免手指与物体产生抓取冲突。

1 手臂抓取运动

手臂抓取过程主要涉及三个组件(延伸、抓取和方向)之间的协调。其中，手臂延伸组件处理手/手腕从起始位置移动到抓取目标物体位置的全部过程；抓取组件包含手指的预成型和合拢阶段；方向组件则用于调整手掌朝向，使之最终与目标物体对齐。

1.1 组件协调

根据Jeannerod的视觉运动通道假说，抓取动作涉及组件分别位于独立的运动通道，通过一个统一的中心控制机制进行时间协调，以维持组件间相对时间的不变性。相对时间不变性，除了指通道运动几乎同时开始和结束，还包括最大抓取孔径基本上发生在运动过程的60%～70%时刻；同时该时刻也时常对应于延伸组件运动加速度最小时刻。文献[2]的最小加加速度模型便是通过指定固定的合拢时间来预估运动所需总时间实现组件在关键时刻的一致性。

抓取运动组件间不仅满足时间协调，还存在空间状态信息的交流。Haggard等对同一目标物体进行了不同速度的抓取，以探讨延伸和抓取组件间的空间影响。结果表明手臂运动速度越快，最大抓取孔径也越大[12]。因此，Haggard构建了一个基于耦合位置反馈的空间协调抓取模型来描述组件间存在的空间状态交流，模型的矩阵方程如式1所示，下标t和a分别表示延伸和抓取组件。

(1)

其中，Ti为组件i的目标状态，Pi为当前状态，ΔPi表示组件i对应的增量，增量矩阵元素Cij表示组件i对组件j的影响。一旦增量矩阵确定，算法将反复更新Pi，使其不断向Ti靠拢，完成抓取动作。

1.2 VITE模型

Bullock等根据点对点手臂运动动力学构建了一个描述手臂运动轨迹的计算模型VITE。VITE不包含自适应学习过程，是一种能描述人类抓取运动特性(如钟形速度曲线、速度精度权衡法则)的生物上可行的机制，具体生物背景参见文献[4]。模型实现了抓取运动组件间的时间等效性[5]。在VITE模型中，不同组件并行运动执行器的起始时间可以不同，但通过一个共同的增量信号可以保证时间的等效性。模型结构如图1所示。TPV代表理想位置，可表示目标物体的体心坐标位置；PPV是当前手臂的位置描述；DV是以上两者的误差向量；G(t)是用于时间协调的门控信号函数。给定目标TPV和初始位置PPV，门控信号开启时，PPV开始不断地对DV和G(t)的乘积进行积分，并输出一个理想速度命令到手臂，使得PPV不断逼近TPV，直到DV为0，此时手臂到达目标位置，延伸动作完成。

Vilaplana指出手指抓取组件同样可采用VITE模型实现，并把抓取孔径看作是由不同自由度(DOF)组成的系统，以模拟抓取过程中拇指和食指之间的距离变化[6]。考虑到抓取的阶段性，即手指先张开到最大角度然后合拢，对应着孔径曲线单调增大到MGA后再减小为物体的实际大小。Vilaplana将目标抓取孔径TA设置为两个连续的目标值(GA1,GA2)。其中GA1表示最大抓取孔径，GA2为实际物体大小。模型通过式2指定TA的连续变化。其中β为积分比例系数，i等于{1,2}。

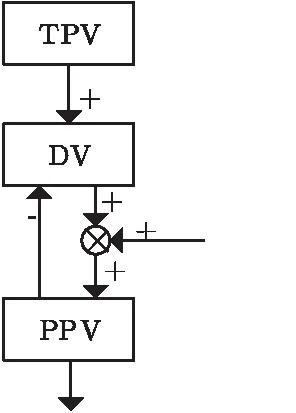
图1 VITE模型示意图

dTA/dt=β(-TA+GA(i))

(2)

由于延伸组件加速度最小时刻对应于抓取角度最大时刻，即手腕移动加速度最小时刻是手指合拢的起始时刻，Vilaplana设置了一个神经元CP用来监测手腕移动的速度和加速度，使得当加速度最小时，有关GA2的信息可以被有效写入，指导手指完成合拢动作。

Vilaplana的工作是卓有成效的，但存在一点问题，那就是对于抓取组件，他所采用的二目标值给定法需要人为设定MGA，这对组件间时空协调的真实性和有效性具有不确定性影响，不能实时地体现抓取过程中手臂运动组件对抓取孔径的空间影响。因此针对这一问题，文中拟通过设置耦合神经元来代替最大抓取孔径的更新转换，实现空间协调，以再现最大抓取孔径形成过程中呈现的各种动态特征。

2 模型构建

文中构建了一种新的解释手臂延伸和抓取过程时空协调的神经模型，参见图2，左侧的VITE模型用于解释抓取运动的运动学特征。模型考虑了手臂延伸(T)、抓取角度(A)和抓取方向(O)三个组件的协调，其中T,D,P分别表示目标、误差和当前的位置向量，下标对应各自的组件。原始VITE中的门控信号G(t)则由右侧的基底神经节丘脑皮层环路表示，基底神经节结构参见文献[13-15]。不同于文献[14]，模型所有组件通过同一个基底核环路门控调节以实现时间等效。神经元Cij表示组件i对组件j的耦合影响，体现组件间的空间协调。针对实验条件发生扰动的情况，模型增设了监督神经元Ei，负责记录本体感受和目标物体内部表示之间的差异，进而进行运动调节。运动前区和辅助运动区(supplementary motor area，SMA)接受感官输入的环境信息，并投射给VITE和基底神经节从而控制运动，同时VITE生成的速度命令也被传递回SMA用于激发后续组件的连续工作。

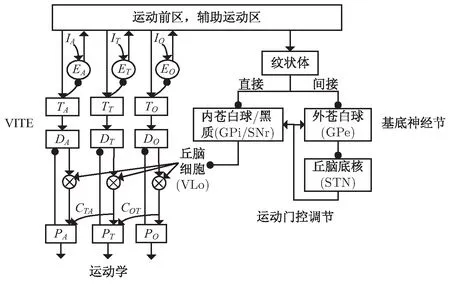
图2 手臂延伸和抓取运动模型

(左侧的VITE模型模拟抓取运动，右侧基底神经节的输出用来调节抓取速度。箭头表示正连接，圆点表示负连接)

参考Bullock的VITE工作等式，设置的抓取组件遵循如下等式：

dDA/dt=α(-DA+TA-PA)

(3)

dVA/dt=αV(-VA+VLo[DA]+)

(4)

dPA/dt=VA+CTA

(5)

dTA/dt=αEA

(6)

其中，TA为目标物体大小，PA为当前抓取角度，DA是以上两者的差值。VLo表示丘脑细胞活度，起着运动初始化和调节速度的作用。CTA表示延伸组件对抓取角度的影响。EA为本体感受IA和内部表示TA之间的差，代表着扰动条件下目标物体大小的变化。α和αV为积分比例系数。延伸组件和方向组件遵循的等式与抓取组件相似，只是在耦合神经元Cij的个数上有所不同，在此不再复述。

不同于Vilaplana的二目标值给定法，新模型采用耦合神经元Cij进行组件间状态信息交流，其中CTA表示延伸组件对抓取组件的空间影响，使之生成最大抓取孔径和合拢过程，COT则用于表示抓取方向变化对延伸组件的影响，进而影响抓取组件。神经元遵循如下等式，其中Vi为Di×VLo的产物，指明了当前通道的运动速度。

dCTA/dt=α(-CTA+ρVT)

(7)

dCOT/dt=α(-COT+ζVO)

(8)

针对目标物体位置、大小、方向发生扰动的情况，模型设置差异细胞Ei完成组件目标(TT,TA,TO)的更新，等式如下：

dET/dt=α[-ET+abs(IT-TT)]

(9)

dEA/dt=α[-EA+abs(IA-TA)]

(10)

dEO/dt=α[-EO+abs(IO-TO)]

(11)

模型右侧的基底神经节电路参见文献[13]。基底神经节的直接通路(direct pathway)和间接通路(indirect pathway)分别表现为削弱和增强苍白球(GPi/GPe)对丘脑VLo细胞的抑制作用。模型遵循的非线性常微分方程如下所示：

dSK/dt=βK[-AKSK+(BK-SK)EK-(DK+SK)IK]

(12)

(13)

其中，SK分别表示壳核(K=1)、内苍白球(GPi,K=2)、外苍白球(GPe,K=3)、丘脑底核(STN,K=4)和丘脑VLo(K=5)的神经元活性；EK和IK分别表示SK受到的兴奋性和抑制性输入。

当运动前区或SMA投射一个运动命令到纹状体，纹状体神经元兴奋后便会释放一种抑制性神经递质GABA，使得直接通路中的GPi对丘脑的抑制作用减弱。丘脑神经元VLo的活动强度也相应增强。式13中，NJ表示直接(J=1)和间接(J=2)通路可用的神经递质的数量。可用神经递质的最大值BNJ是多巴胺水平的函数(BNJ(DA)=1,DA=1,J={1,2})。

相比于文献[6]设置固定的G(t)函数进行运动调节，新模型基于神经解剖学和生物学构建的基底神经节丘脑皮层环路使得手臂抓取运动更具生物学意义，增设的耦合神经元也更能反映抓取过程的各种动态特征，有效地解决了手臂运动跟踪的问题，具有更好的运动协调功能。

3 仿 真

文中将对新模型进行多种情况的仿真，包括不同抓取速度、实验条件扰动等。仿真中基底神经节丘脑模块涉及的参数为：βK=(1,2,1,1,5),AK=(10,3,3,10,2),BK=(1,3,2,2,2),DK=(0.0,0.8,0.8,0.8,0.8),K=(1,2,3,4,5)。网络的兴奋性EK和抑制性IK输入分别为：E1=I(t)+Iach+f(S1),E2=10S4+f(S2),E3=10S4+f(S3),E4=IS+f(S4),E5=0.2;I1=0.0,I2=50S1N1+0.2S3,I3=50S1N2+0.2S2,I4=10S3,I5=0.5S2,其中f(x)=x3/(0.3+x2)。

3.1 基本抓取动作

为了测试新模型的抓取性能，对Vilaplana模型的抓取实验进行了仿真，设置目标物体直径TA为2 cm，起止点位置距离TT为30 cm。仿真结果如图3所示。手腕运动速度呈现钟形曲线，抓取孔径的变化表明了抓取过程中手指先是张开到最大角度然后合拢收缩直至完成抓取。两个组件在基底神经节丘脑环路的时间协调下同时开始、同时结束，最大抓取孔径的产生也表明了组件间的空间耦合神经元CTA发挥了作用。相较于Vilaplana的二目标值给定法，新模型利用耦合神经元进行抓取协调，使得手臂运动的延滞时间缩短7.57%，上升时间缩短7.47%，调节时间缩短10.4%(假定稳态误差为±5%)。抓取孔径的最大超调量增加了21.4%(速度加快使得孔径增大)，延滞时间缩短23.9%，上升时间缩短26.1%，调节时间缩短了13.3%。

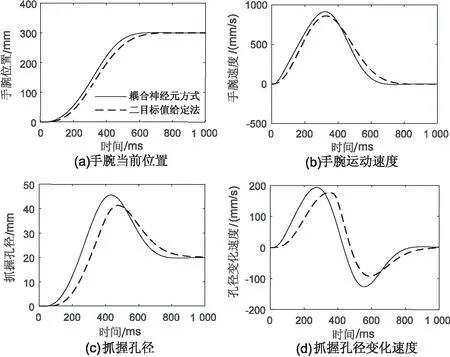
图3 基本抓取动作的对比仿真

3.2 不同速度的仿真

图4是不同速度下抓取运动的仿真，(a)、(b)分别表示抓取过程的运动速度和孔径变化，(c)、(d)为VLo和GPi细胞的活动强度。仿真中，基底神经节网络的输入I初步分为3个等级，即I=0.1表示低速运动的轨迹，I=10对应于高速运动，I=1则是上述两者之间的轨迹。纹状体的输入来自运动或运动前区。由图可知，随着纹状体输入强度的增大，手腕运动速度的峰值也逐渐增大，运动时间也相应变短。同时最大抓取角度随着手腕速度的增大而增大，体现了组件间的空间协调。基底神经节中，GPi和VLo细胞的活动强度呈现出一定的反比关系，运动皮层输入强度增大，纹状体对GPi的抑制作用增大，导致GPi对丘脑细胞的抑制作用减弱，VLo活动强度也相应增大。

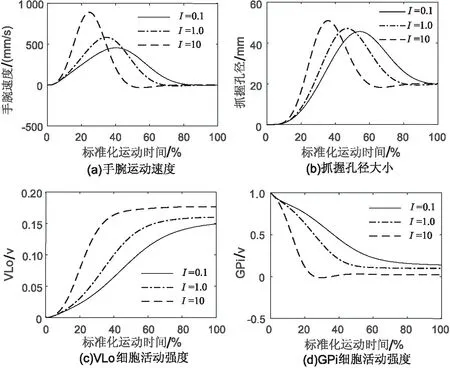
图4 3种速度下的抓取动作仿真

3.3 目标距离扰动实验

图5是目标抓取物体距离变化情况下的抓取动作仿真，实验设置目标物体直径TA为1.5 cm，起止点位置距离TT初始15 cm，100 ms后增大为45 cm，目标方向TO为0°，表示当前物体方向与手肘对齐。仿真结果的第一、二列分别表示延伸和抓取组件各个指标的当前状态，第四行表示耦合神经元发挥的作用。从图中可以看出，目标距离TT的扰动使得当前距离PT和手腕速度VT曲线发生改变。同时由于CTA的耦合影响，抓取角度曲线PA出现了合拢张开再合拢的过程。由于TO初始设置为0°，且未发生方向扰动，方向组件暂未发挥出实际作用。

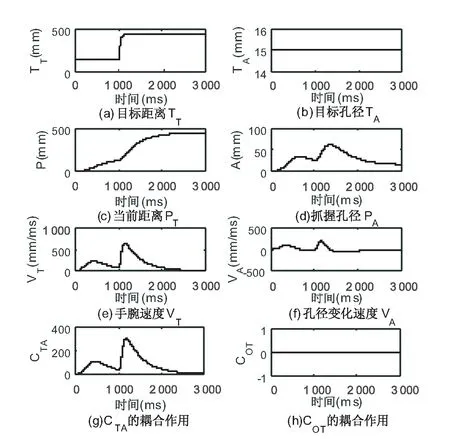
图5 目标距离扰动实验

3.4 目标位置扰动实验

图6是目标物体位置变化情况下的抓取动作仿真，实验设置目标物体直径TA为1.5 cm，起止点位置距离TT初始15 cm，目标角度TO初始为0°，100 ms后TT增大为45 cm，TO偏离手肘15°。仿真结果显示，目标物体位置扰动不仅使得延伸和抓取组件发生变化，同时方向组件也开始工作，并通过耦合神经元COT影响着抓取运动。实验数据对比发现，相较于距离扰动实验，目标位置扰动情况下的手腕抓取速度略微加快，以补偿方向扰动带来的影响。

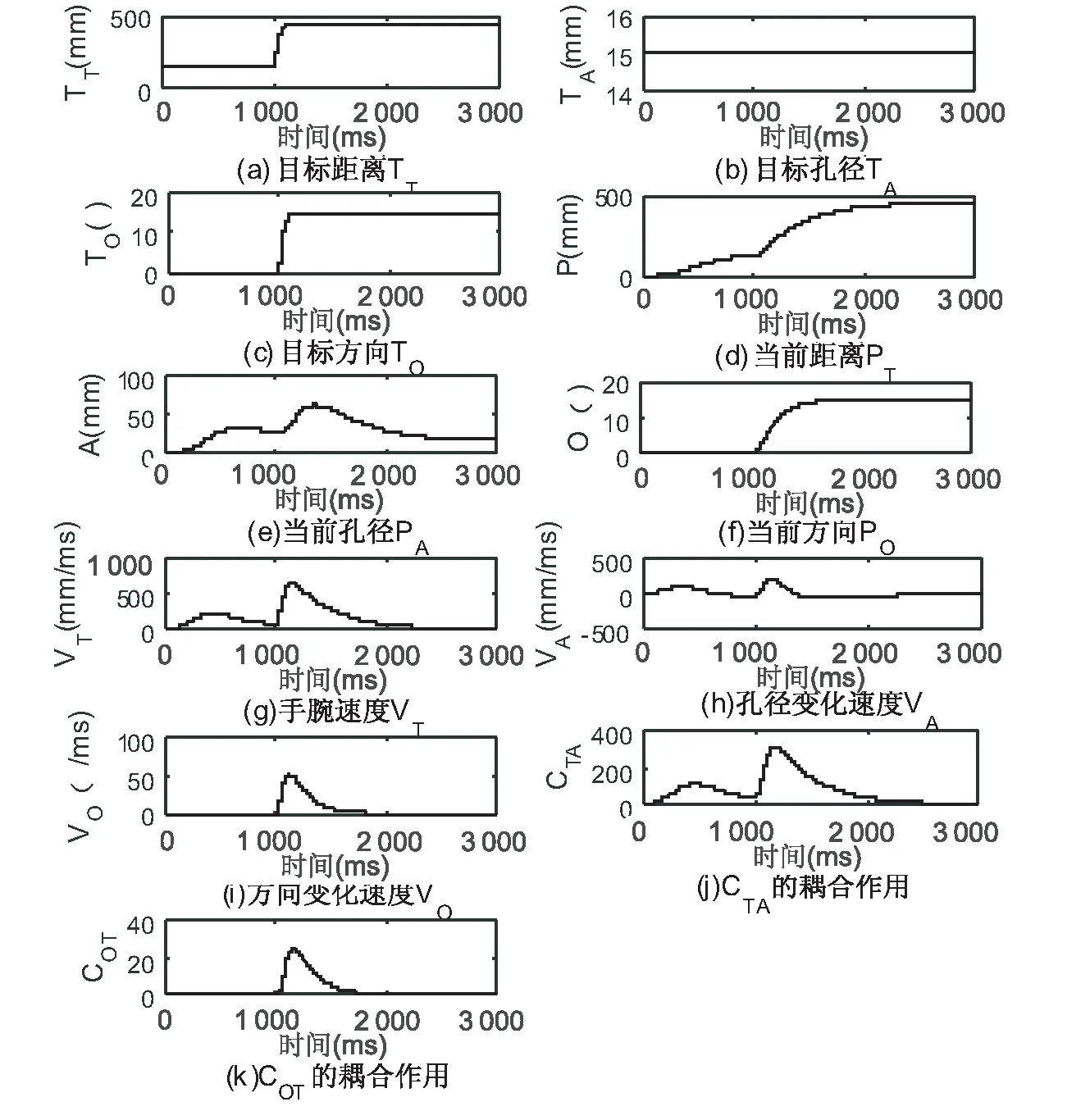
图6 目标位置扰动实验

3.5 模型对比

新模型以Jeannerod提出的人类抓握概念模型为基础，设置三个由基底神经节定时机制统一协调的、独立运行的视觉运动信道(移动、抓取和方向组件)，并利用具有生理表征的VLo信号和耦合神经元改进了前人处理组件时空协调的方法。

基于相同假设条件下，新模型与其他计算模型存在某些概念上的相似和差异性。这些模型共同指出，抓取运动的不同信道间仅存在着唯一的一个时间交互，通过建立一个时间片来表示抓握初始张开阶段的结束以及手指最终合拢阶段的开始。而模型间的具体差异是时间片的决定方式。Vilaplana模型中，这种时间片主要来源于与手部移动加速度相关的假定的传入信号(假设CNS能够从主要的身体感受信号中得到这种信号)。Hoff-Arbib模型是在运动开始前，对手指预成型组件进行预计算以及利用假定的时间运动组织单元确定合拢时间常量。而新模型则是利用速度和方向的单相控制调节来代替抓握角度的双相控制，大大简化了抓取任务假定在大脑F5区域所进行的过程。

在抓取方面，文中将抓取孔径定义为食指和拇指之间距离相关的理想标量，而Vilaplana等基于主成分分析法仅用两个参数低维控制手指关节协调，为手势库的建立提供了新思路[16]。因此，在具体手势跟踪应用方面，模型可参照该手势协同控制方案完成手指关节角度的生成与手势建模，指导多指灵巧机械手的运动与抓取。

在文献[17]中，笔者提出了一种控制模拟仿生机械臂延伸运动的小脑学习模型。该模型利用脊髓反射线路的伺服机制，将神经网络嵌入模拟哺乳动物的控制系统，用以控制6肌肉块2关节的平面手臂，真正从生物学意义上实现了并行分层控制的方法。文中将新模型作为轨迹生成器嵌入该控制系统，使其快速学会精确轨迹控制。仿真结果表明，通过将脊髓层次上的轨迹误差检测与小脑中的记忆轨迹相结合，嵌入的控制系统能对快速手臂延伸运动进行精确的鲁棒控制。

4 结束语

针对手臂延伸和抓取运动的时空协调问题，提出了一种基于基底神经节丘脑皮层环路结构进行时间协调、通过耦合神经元进行空间协调的神经网络模型。模型再现了基本抓取动作的基本特征，保证了并行组件间的时间等效性，生动地描述了抓取孔径受其他组件影响的空间因素，且无需对运动时间进行预计算，无需人为干预最大抓取孔径的生成过程，增设的耦合神经元也更能反映抓取组件间的空间状态关联性。通过对模型进行不同速度和扰动情况的仿真，结果表明，该模型具有良好的运动协调性和抗干扰性。然而，模型只考虑了基底神经节这一生理结构，忽略了小脑与基底神经节、丘脑的生物联系以及小脑对躯体运动的调节作用[18]。笔者也曾在文献[9]中探讨了小脑对手臂抓取的时间协调功能，因此下一步研究方向是结合小脑和基底神经节，研究两者对手臂抓取运动的共同调节和认知指导作用。