压裂作业效果多元线性回归模型及措施技术经济界限

梁甲波 卢岩 姚佳杉

1.中国海洋石油伊拉克有限公司油井作业中心；2.中国海洋油服中东公司；3.中石油华北油田公司第一采油厂

国内某油田三类储层有效厚度小、渗透率低且层间及平面非均质性严重［1-2］，在高含水后期剩余油分布高度分散，主要通过压裂增油［3］，准确地预测压裂增油效果及确立合理技术经济界限尤为重要。

目前油田压裂增油效果预测主要通过2种途径：一种是采用油田认可的经验公式法，主要为logistic curve模型与递减模型相结合的办法，这种方法更适用于宏观预测开发指标的变化规律，落实到各井网及单井增油效果的评价就明显不适用［4］；另一种是从渗流机理出发，构建数学模型，同时结合解析法进行增油预测，为了模型的准确性和全面性而引入的参数较多，在现场实际应用时获取难度较大［5-7］，适用性受局限。而对于高含水期油田措施技术经济界限的研究，最新实施模式是首先结合经济效益确定目标增油量，再应用统计法，根据绘制的已措施井初期增油量与各指标分布图版，确定该增油量下的各指标界限值［8］。

多元线性回归模型预测压裂增油效果在油田已有应用［9-10］，但考虑到各项指标与增油效果并非都是线性分布规律，同时压裂措施在不同井网收效差异较大，故提出先应用函数关系将两者非线性规律转换成线性规律，再引入多元线性回归模型，进而结合油价确定不同井网主控因素的实施界限。

1 压裂增油数学模型

1.1 多元线性回归模型

考虑到不同措施井之间的增油量实际值存在较大差异，将各井措施增油量与该井措施前产油量的比值，即增油幅度作为因变量。应用多元线性回归法，将各因素对增油幅度的影响作为线性空间的一组基，则因变量增油幅度ΔQ/Q可以表示为n维线性空间。将各项指标对增油幅度的影响X1，X2，…，Xn作为一组基，其中ai（i=0，1，2，…，n）为回归系数，则增油幅度n维线性空间ΔQ/Q可表示为［11］

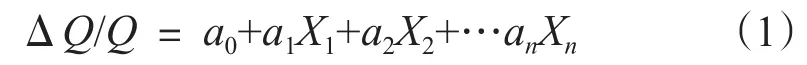
多元线性回归分析要求各影响因素之间相互独立，且每个因素与整体均呈线性分布规律［12］，但实际压裂效果与各影响因素通常并不呈线性分布规律，故提出先用压裂井的增油数据与措施前该井生产数据计算出实际增油幅度作为因变量，每口井的各增油影响因素作为自变量，分别进行分布规律函数拟合。通过拟合出的函数关系，将各因素与整体的非线性规律通过此函数转换成线性规律，即

最后利用最小二乘法求多元线性回归方程需进行显著性检验［13］。通过查表确定显著性水平α下的临界值Fα，当计算的F值大于临界值时，认为所建立线性回归方程是显著的。

1.2 各因素与增油幅度关系

根据压裂增油机理及措施工艺要求，确定了5项与压裂效果相关的影响因素，包括：砂岩厚度、有效厚度、措施井含水率、层段渗透率变异系数、措施前产液量。根据多元线性回归模型建立条件，首先应用无重复双因素分析判断各因素与增油幅度是否相关，在两者相关的基础上再用不同类型函数进行拟合，将相关系数最大的作为两者分布规律函数类型。下面以砂岩厚度为例进行说明。

措施砂岩厚度是影响压裂增油效果的一项重要参数，根据产能公式，油井产能与储层厚度呈正比。在进行压裂措施时，因三类储层厚度较小，压裂裂缝高度通常能覆盖整个储层厚度，因此措施砂岩厚度越大，压裂后所改善的储层厚度就越大，增油效果越好。为了消除其他因素对增油幅度的影响，对该油田除了措施砂岩层厚度外其他指标接近的30口已压裂井进行统计，作为该研究的特征点，具体见表1。

为了判断压裂目的层的砂岩厚度和增油幅度是否存在相关性，首先对两者进行了无重复双因素分析，结果表明在显著性水平α=0.05的条件下，计算得到F=64.7349，远大于临界值Fcrit=4.183；同时，P值为7.14×10-9，远小于显著性水平，所以认为两者具有显著相关性。绘制增油幅度-措施砂岩厚度散点图，去除败点，分别用对数型、二次型、幂函数型和指数型趋势线进行拟合（图1），从相关系数的角度来看增油幅度与措施砂岩厚度更符合对数型规律。

同样，选取不同压裂井作为特征点，对其他各项可能的影响因素，如压裂层措施有效厚度、措施前产液量、目的层渗透率变异系数和措施井含水率，与油井增油幅度分布规律进行拟合，具体结果见图2。经函数拟合得知，增油幅度分别与上述各影响因素分别满足指数型分布规律、二次型分布规律。

表1 样本井基本数据Table 1 Basic data of sample well

图1 增油幅度与措施砂岩厚度拟合曲线Fig. 1 Fitting curve between oil increment amplitude and stimulated sandstone thickness

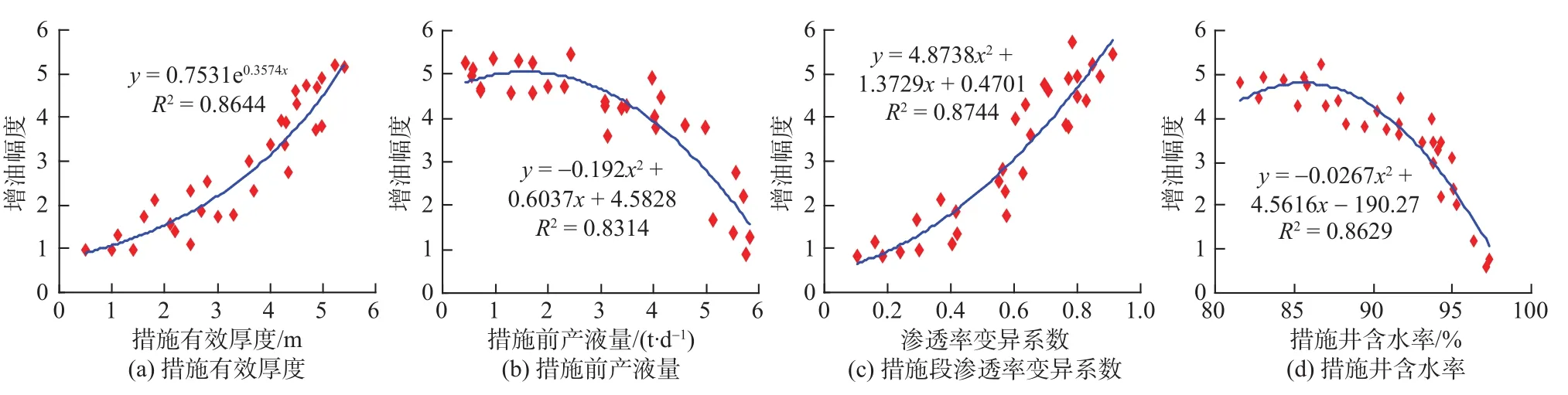
图2 增油幅度与不同影响因素拟合曲线Fig. 2 Fitting curve between oil increment amplitude and in fluential factors

1.3 多元线性回归模型的建立

经过上述分析和函数拟合，找出了压裂增油幅度与各项因素之间的分布规律，然后在此基础上建立了压裂增油效果的多元线性回归模型。

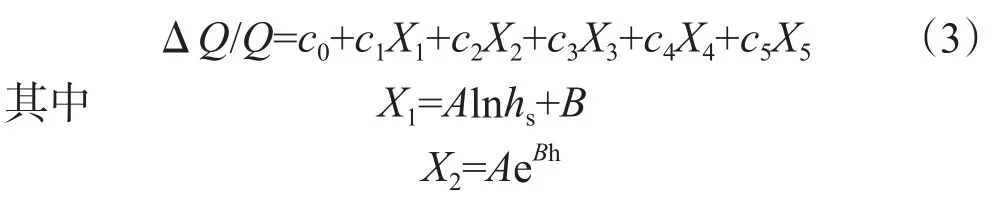
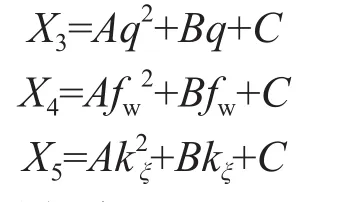
式中，ΔQ/Q为增油幅度；X1、X2、X3、X4、X5分别为砂岩厚度、有效厚度、措施前产液量、全井含水率、层段渗透率变异系数的回归公式；c1、c2、c3、c4、c5分别为砂岩厚度、有效厚度、措施前产液量、全井含水率、层段渗透率变异系数对增油幅度贡献率；hs为措施砂岩厚度，m；h为措施有效厚度，m；q为措施前日产液量，t/d；fw为全井含水率，%；kξ为层段渗透率变异系数。

1.4 增油模型在国内某油田的应用

考虑到压裂措施在不同井网受效不同，导致根据实际数据回归出的增油模型也不同，为了细化研究，统计了国内某油田已进行压裂井的各项指标实际数据，建立了不同井网的压裂增油模型。同时由于压裂措施主要针对薄差储层，故以该油田的二次井网压裂井实际数据为例，建立其增油模型。

将二次井网压裂施工井各项指标的实际数据进行统计，并将压后增油幅度与这些指标公式之间的系数进行回归，通过拟合函数将各指标与增油幅度之间的非线性关系转换为线性关系之后，应用回归分析法确定各项指标对增油幅度的贡献率，建立二次井网压裂增油模型，结果为

对所建立的压裂效果多元回归模型进行显著性分析，在显著性水平α=0.05的条件下，计算的F值为27.51，大于临界值F0.05（4，5）=5.19，同时P值为8.398×10-10，远小于0.01，认为所回归的模型具有显著性。

应用二次井网多元线性回归增油模型计算各特征井增油幅度并与每口井实际增油幅度进行对比，如表2，实际平均增油幅度1.95，应用增油模型计算的平均增油幅度为1.93，误差为1.03%；单井对比增油幅度平均误差为7.43%。

2 压裂界限研究

目前压裂措施界限研究主要是结合油价计算盈亏平衡点，根据初期增油量统计学结果，给出不同油价下的措施井次［14-16］。提出应用各井网已建立的增油模型，结合影响各井网压裂措施效果的主控因素，根据不同油价计算盈亏平衡点处的最小增油幅度，反算各井网主控因素的技术界限。

表2 二次井网措施井实际增油幅度与计算值对比结果Table 2 Comparison between actual oil increment amplitude and calculation value of stimulation well in secondary well pattern

2.1 各井网主控因素的确定

利用不同井网所建立的增油模型反算措施实施界限是对本文增油模型的一项创新性应用。然而，对于每项指标的界限都一一给出对现场施工制约性较大，故提出要根据模型中回归系数的意义，即各项影响因素对增油幅度的贡献权重大小，将回归系数最大的2项指标作为该井网的主控因素，各井网只给出2项主控因素的经济界限值。结合该油田实际数据，各井网增油模型系数回归结果见表3。

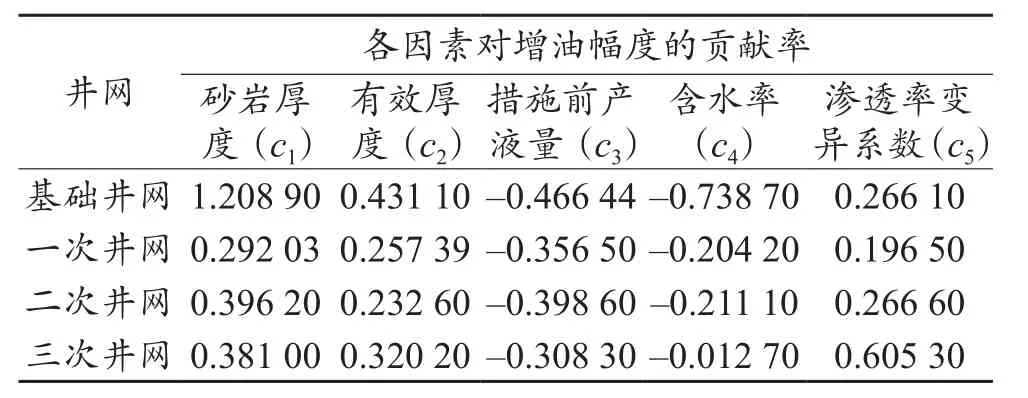
表3 各井网增油模型系数回归结果Table 3 Coef ficient regression results of each well pattern in oil enhancement model

在表3各井网增油模型系数回归结果基础上，通过比较各项指标的权重值，确定各井网的主控因素，可以看出，压裂层位的措施厚度是影响压裂效果的主要因素，在各个井网权重值都最高，但是各井网另外一项主控因素存在差异：基础井网挖潜对象的储层物性好，投产也最早，含水率普遍高于其他井网，因此含水率是基础井网的第2个主控因素；对于一次井网和二次井网，因为储层物性较基础井网略差，但仍有开发潜力，故措施前产液量较低的，压裂效果更好；对于物性最差、多为表外储层的三次井网，压裂目的层的差异对压后生产效果影响最大，所以渗透率变异系数是该井网的第2主控因素。

2.2 不同井网技术界限的确定

由于所建立的增油模型是增油幅度与多项影响因素回归而成，不能直接应用增油量计算其中某一项主控因素界限值，但考虑到井网内部各影响因素之间差异不大，因此在反算某一项指标技术界限时其他指标采用样本点平均值，同时用平均措施前产油量和最小增油量确定最小增油幅度。各井网技术界限计算结果见表4。

表4 不同油价下各井网技术界限Table 4 Technical limit of each well pattern at different oil prices

3 模型应用效果

所建立的增油模型是应用国内某油田各井网已压裂井的实际数据进行回归的。根据增油模型建立的技术界限划分方法指导了该油田示范区在控水提效项目期间的压裂实施，并结合压裂井动、静态数据，进行了增油效果预测。考虑到截至目前示范区控水提效项目期间压裂措施量较小，为了增大样本数量，统计了示范区与示范区相邻区块2016年初至2018年6月间二次井网所进行的14口压裂井实际数据，应用公式（4）预测每口井增油幅度，并与实际相比，验证增油模型预测效果的可靠性（见表5）。

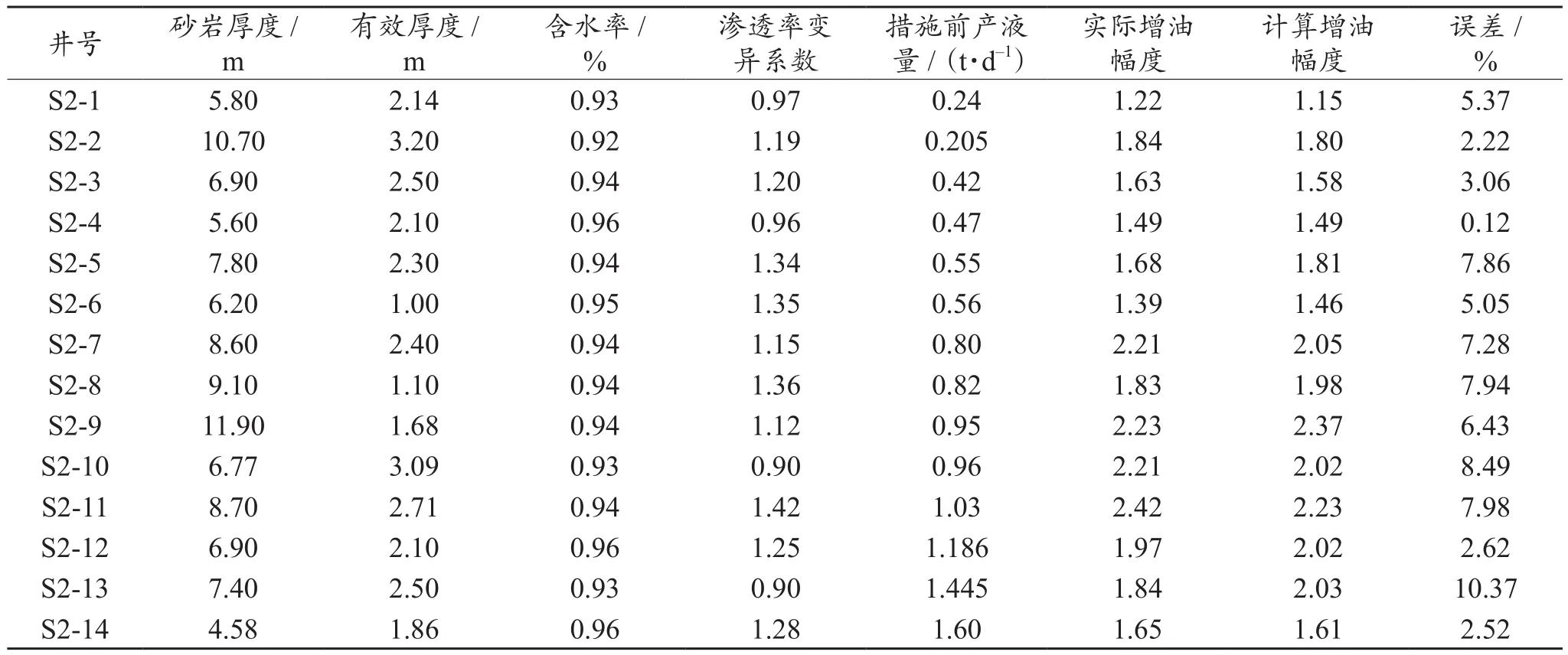
表5 模型应用效果Table 5 Application effect of the model

由表5可知，应用增油模型计算的增油幅度与现场实际增油幅度对比，拟合程度较高，平均单井增油幅度计算误差仅为5.52%。这是由于此模型的建立是应用该区块之前已压裂井的大数据进行回归的，因此接下来预测相同区块压裂井措施效果适应性明显较强。

4 结论

（1）根据压裂增产原理，筛选了与压裂增油量相关的压裂目的层砂岩厚度、有效厚度、措施前产液量、油井含水率、储层渗透率变异系数等5个指标，并结合实际数据，建立了包含这5项指标的各井网压裂效果多元线性回归模型。

（2）将国内某油田以往压裂井的实际储层及生产数据作为特征点，通过研究5项指标与压后增产幅度之间的函数关系，建立了该油田的二次井网压裂增产多元线性回归模型，并通过了显著性检验。

（3）提出基于不同井网的压裂效果预测模型，确定了影响不同井网的主控因素，并且根据不同的油价给出了技术界限。同时结合现场实际数据，验证了模型的可靠性。