一类非线性时滞系统的状态反馈跟踪控制

关涌涛，贾永锋

(1.安阳师范学院 软件学院，河南 安阳 455000；2.安阳市中等职业技术学校，河南 安阳 455000)

0 引言

控制系统中，时滞常表现为信号传递的延时等，这种不确定性会对整个控制系统的性能造成不利影响[1]。对线性系统控制，常常采用线性矩阵不等式(Linear Matrix Inequalities, LMI)[2-3]来处理系统中的时滞，但这种方法难以应用到非线性系统中来。近年来，非线性系统时滞问题的处理常借助构造合适的Lyapunov-Krasovskii泛函处理，并取得了一些重要的成果[4-9]。

模糊逻辑系统也常常被应用于非线性系统的控制问题中[10-12]。初期，模糊逻辑控制(FLC)被发展为一种模型无关的控制器，尽管在许多工业应用中获得了巨大的成功，但由于缺乏严格的系统化的稳定性分析和控制器设计准则而受到很多质疑。接着，模糊逻辑系统被证明为一种良好的非线性逼近器[10]，继而也被越来越多的被应用于基于模型的自适应控制中，闭环系统的稳定性和控制性能都可以得到严格的证明。与神经网络(NN)相比，FLS由于可以建立IF-THEN规则而可以同时利用数值信息和专家信息，因而具有更快的收敛速度。文献[11-13]针对未知非线性系统，利于FLS逼近其中的不确定项，并根据Lyapunov理论建立了稳定的控制器。上述文献虽然针对非线性时滞系统控制问题进行了研究，但就笔者所知，针对含有完全未知时滞的系统展开讨论的结果并不多见。

本文研究了一类含有完全未知时滞的非线性系统的温度控制问题。模糊逼近器处理含有未知时滞的非线性函数，放松了对非线性时滞函数的要求；利用参考信号代换未知时滞，避免了对未知时滞信号的微分，从而使控制器是不依赖于时滞的。此外，本文还对未知的Lipschitz常数采用了自适应的方法处理。上述代换产生的辨识误差和代换误差则在自适应Backstepping设计过程中采用自适应边界技术处理。

1 问题描述

考虑以下SISO非线性时滞系统

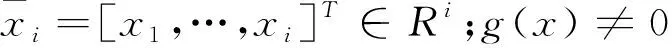
控制目标：设计无记忆自适应模糊控制器，使闭环系统所有信号半全局一致最终有界，同时跟踪误差能够收敛到原点附近的小邻域内，即

(2)

其中ω>0为一常数且可以为任意小。

假设1[14]：目标轨线yr(t)及其前n阶导数已知，且在区间t∈(-∞,∞)上一致有界。

2 模糊辨识

考虑如下模糊推理规则

R(t):IFx1isF1land…andxnisFnlTHENyisGl

(3)

其中x=[x1,…,xn]T∈X=X1×…×Xn⊂Rn和y∈Y⊂R分别是模糊逻辑系统的输入输出，Fil和Gl分别是定义在语言变量Xi和Y上的模糊子集，l=1,2,…,M指M条规则中的第l条。当上述规则表示的FLS采用单点模糊化、乘积运算的模糊蕴涵、重心法解模糊和高斯函数的隶属函数时，可以表示为[5]

(4)

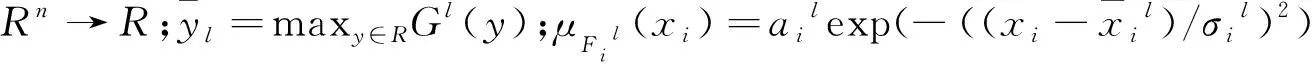
(5)

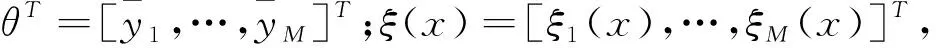
(6)

FLS满足如下Lipschitz条件[11]，其中的l为Lipschitz常数：

|y(xl|θ)-y(x2|θ)|=|ξ(x1)Tθ-ξ(x2)Tθ|≤‖x1-x2‖l

(7)

不等式(7)在自适应控制器的设计过程中起到了非常重要的作用。

引理1 (一致逼近定理)[10]：对于在紧集X⊂Rn中的任意实值连续函数f(x)和任意ε>0，存在一个由(5)定义的y(x|θ)，使得d∞(f,y)=supx∈X|f(x)-y(x|θ)|<ε。

根据引理1，在紧集Xi⊂R上，(1)式中的hi(y(t-τi))可由以下有qi条规则的FLS逼近

hi(y(t-τi))=ξi(y(t-τi))Tθi+εi(y(t-τi))

(8)

其中ξhi=[ξhi,1,…,ξhi,qi]T为(5)式定义的模糊基函数向量，θi∈Rqi的定义见式(5)，εi为逼近误差。将上式(8)代入(1)式，得

其中

θ=[θ1T,…,θnT]T

εi=εi(y(t-τi))

假设2[10]：在紧集Xi⊂R,i=1,…,n上，模糊辨识误差小于某一未知常数ψ1≥0：

|εi|≤ψ1

(10)

由于采用了模糊逼近，本文仅要求系统(1)中的非线性时滞函数连续，这样便放松了文献[8-9]对非线性时滞函数的要求。然而完全未知的时滞τi仍然存在于(9)式的矩阵函数φi中。众所周知，在应用Backstepping的思想对式(9)进行控制器的设计过程中，需要对φi求导，因此φi中的未知时滞便构成了控制器设计的主要障碍。为了解决这个问题，本文采用时滞代换的方法处理未知时滞。将时滞信号y(t-τi)用yr(t)来代换，那么式(9)变成

其中，ei=[φi(y(t-τi))-φi(yr(t))]Tθ为时滞代换误差。比较(1)和(9)式，(11)式中所用的技巧只是加减了一项φi(yr(t))Tθ，但正是这种技巧避免了对未知时滞信号的微分，从而可以使无记忆控制器的设计成为可能。

在得到(11)式之后，无记忆控制器设计的主要障碍转化为对时滞代换误差ei的处理。设pi=[φi(y(t-τi))-φi(yr(t-τi))]Tθ，ωi=[φi(yr(t-τi))-φi(yr(t))]Tθ，那么有ei=pi+ωi，这样时滞代换误差被分成两项。根据(7)式，pi和ωi满足下述不等式

对于上式(12)中的第二个不等式，根据假设1，可知|yr(t-τi)-yr(t)|有界，又因bi为常数，因此可得ωi有界。取Ψ2为大于或等于max{sup(|ω1|),…,sup(|ωn|)}的常数，则有

|ωi|≤Ψ2

结合上式，定义误差vi=εi+ωi，并令Ψ=Ψ1+Ψ2，则有

|υi|=|εi+ωi|≤|εi|+|ωi|≤Ψ1+Ψ2=Ψ

(13)

这里需要说明的是，由于函数hi不满足所示的Lipschitz条件，因此不能直接对其进行上面的时滞代换，因此需要先进行FLS逼近。不等式将在下式中用于处理误差项。将yr(t)简记为yr，系统可进一步写为

虽然含有不确定的项υi和pi，(14)式已经可以利用Backstepping思想进行控制器的设计。不定项υi和pi将在下一节基于Backstepping 思想设计控制器的过程中，利用自适应边界技术以及在稳定性分析中通过构造Lyapunov-Krasovskii泛函的方法予以消除。

3 自适应控制器设计

首先定义系统误差向量z=[z1,…,zn]T和坐标变换

其中αi-1为待选的稳定化函数。

Step1：从(15)式，有

(16)

沿(14)式对z1求导，得

(17)

其中w1=φ1(x1),ζ1=υ1,P1=p1

选择的第一个稳定化函数是

(18)

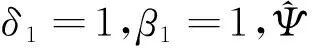
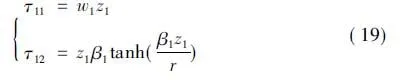
Stepi(i= 2,…,n): 从(15)式，有

xi+1=zi+1+αi+yr(i)

(20)

i可以取n是因为，如果做以下定义，则最后一步i=n将包含在(20)式中[14]

αn=g(x)u-yr(n),zn+1=0

(21)

沿(14)式对zi求导，得

(22)

其中

调节函数选择为

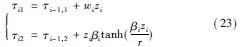
稳定化函数选择为

(24)

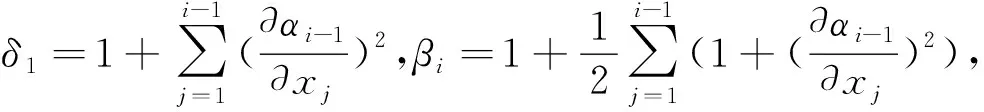
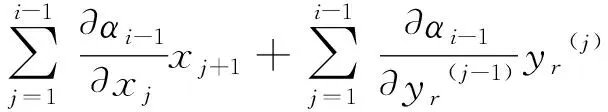
σj2=0

参数自适应律选择为

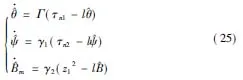
控制律u可根据(21)式计算如下，其中的an由(24)式确定

(26)

由于(24)式中的an已经和输出时滞y(t-τi)完全无关，因此(26)式表示的控制律u和输出时滞y(t-τi)完全无关，因此本文得到的控制器(26)是完全不依赖于时滞的，即无记忆的。

4 主要结果

根据上文，可得闭环系统如下

(27)

利用|η|≤ηtanh(η/r)+κr，κ=0.2785中的辨识误差ζi可以处理如下[6]

(28)

由式(12)可得

pi≤|y(t-τi)-yr(t-τi)|bi=|z1(t-τi)|bi

(29)

利用Young不等式(29)，(27)不等式中的时滞项pi可以处理如下

(30)

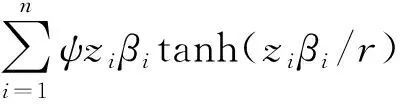
定理2：在假设1-2的条件下，系统(1)，控制律(26)和参数自适应律(25)组成的闭环系统具有以下特点：

2) 跟踪误差满足

(31)

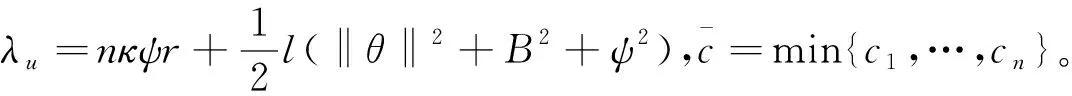
证明：定义Lyapunov-Krasovskii泛函如下

V=V1+V2

(32)

其中，V1和V2的定义如下

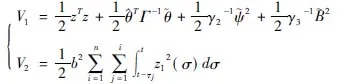
对V1和V2求导，可得

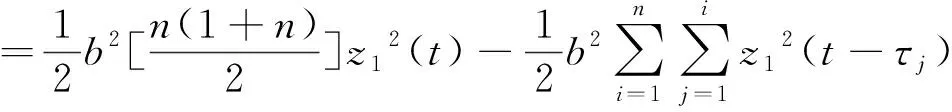
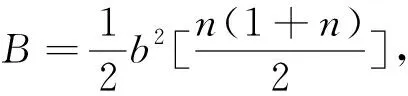
-τj)+L+nψκr

(34)

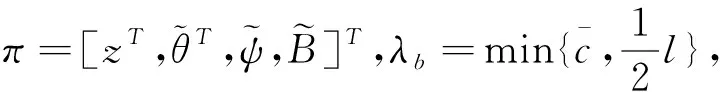
(35)

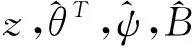
2) 根据(34)式，有

由(36)式可以证明式(31)成立。从(31)式可以看出，通过调节设计参数r,l和ci，可以使跟踪误差能够收敛到原点附近的一个任意小的邻域内。

5 仿真研究

考虑以下未知非线性时滞系统

(37)

其中，未知时滞τ1=5，τ2=2；控制器的设计目标是跟踪参考信号(sin(t)+sin(0.5t))/2。在设计过程中，控制器中并不出现时滞项，因而与时滞τ1、τ2完全无关。

模糊集的语言值取为：正大(PB)，正小(PS)，零(ZO)，负小(NS)，负大(NB)。对h1、h2，可定义模糊隶属函数为μNB=e-10(x+1)2，μNS=e-10(x+0.5)2，μZO=e-10x2，μPS=e-10(x-0.5)2，μPB=e-10(x-1)2，如图1所示。

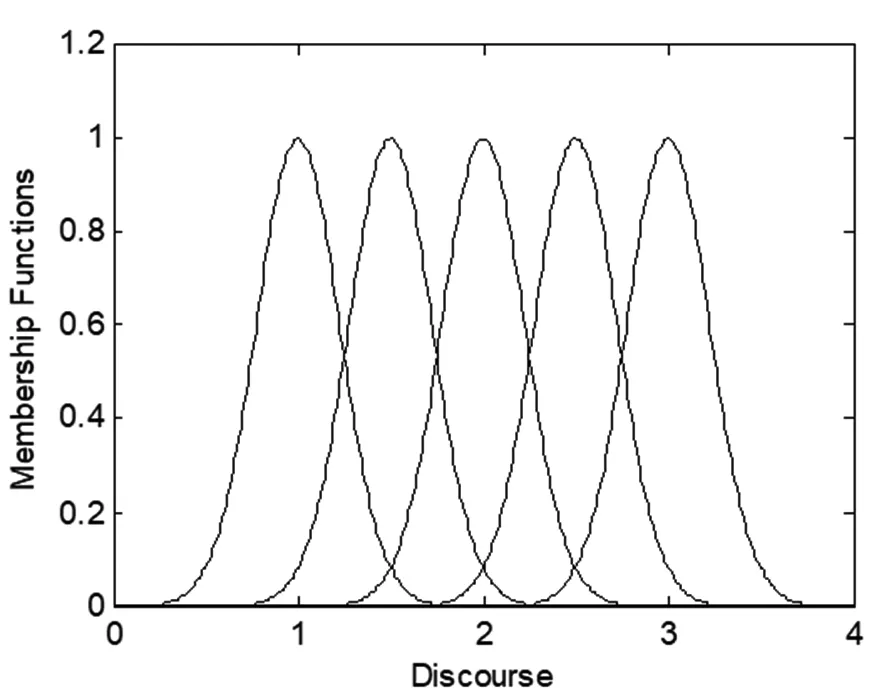
图1 模糊隶属度函数

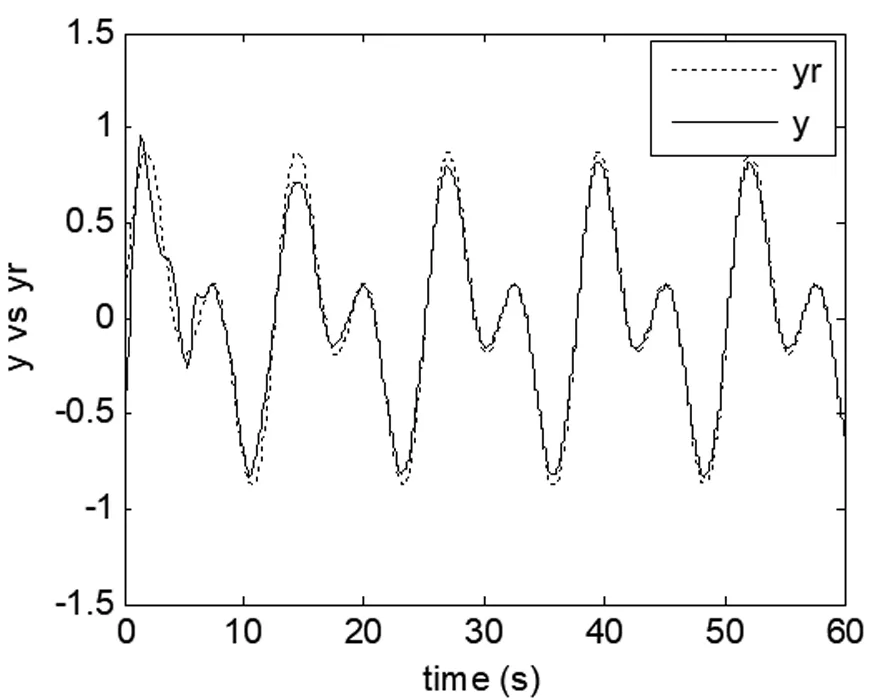
图2 系统输出y,参考信号yr

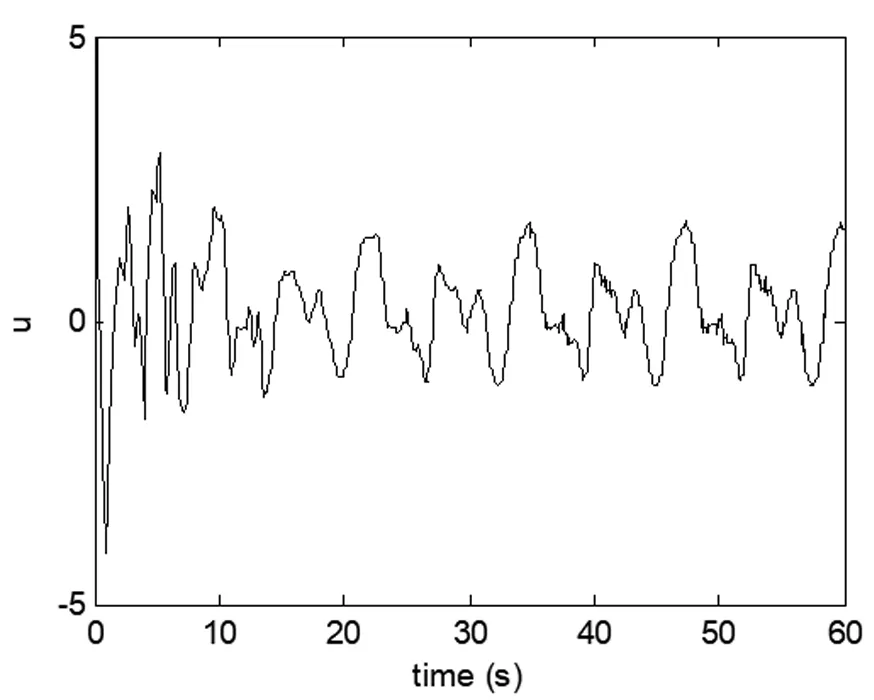
图3 控制输入u

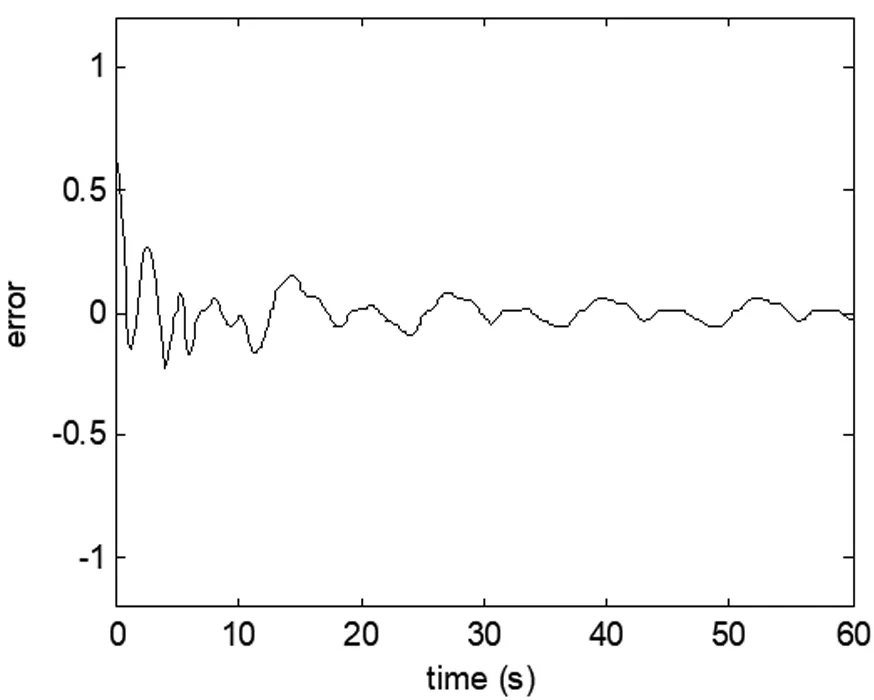
图4 跟踪误差

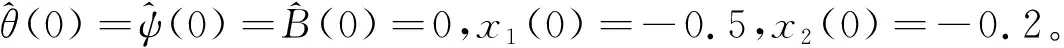
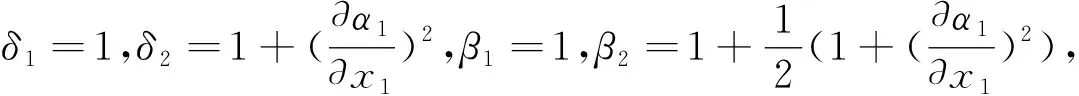
参数自适应律为

仿真结果如图2-4，图中可以看出所设计的控制器能够实现很好的控制效果。

6 结论

本文解决了一类非线性时滞系统的自适应模糊跟踪控制问题。模糊逼近器和时滞代换技巧的使用，使得所设计的控制器是不依赖于未知时滞的，这扩大了本文方法的应用范围，便于推广。如何将本文算法推广到输出反馈的系统中，得到不依赖于时滞的自适应输出反馈跟踪控制器，仍然是一个值得进一步研究的问题。