地震荷载作用下确定土的阻尼比的频域分析法

马倩倩， 刘保健， 吴明玉，3， 韩 珏

(1.南阳理工学院， 河南 南阳 473000； 2.长安大学 公路学院， 陕西 西安 710064；3.西北农林科技大学， 陕西 杨凌 712100； 4.商洛学院， 陕西 商洛 726000)

1 研究背景

土的阻尼比是土的一个重要动力特性参数[1]，它的确定一直是土动力学研究中的重要问题。现行土的动阻尼比室内试验确定方法，仅适用于周期荷载作用下土的阻尼比的确定，并且这些确定土阻尼比的方法都依据单自由度和阻、弹系统的有阻尼自由振动理论，将所有阻尼力产生的能量损耗都等效为土黏弹性的能量损耗；因而采用传统的方法不能合理地计算随机地震荷载作用下土的阻尼比，更不能分析地震荷载作用下的不同频率对阻尼比的影响。地震荷载是比较常见的随机荷载，在实际工程中相关场地的抗震设计要求的阻尼参数都是依据现有的参考值来确定的，与实际地震荷载作用下土的阻尼比是不相符的。为了合理确定地震荷载作用下土的阻尼比，为工程提供合理的动力特性参数，有必要对随机荷载作用下土的阻尼比的确定方法进行研究。

许多研究采用等效线性模型法计算土的阻尼比，通过试验分析动应变、循环次数、孔隙比等因素对不同类型的土的动阻尼比的影响[2-11]；李晶晶等[12]、黄志全等[13]和张雨廷等[14]采用对数衰减率法计算了共振柱试验中土的阻尼比；应怀樵等[15]采用半功率带宽法与INV阻尼计法求材料的阻尼比；刘保健等[16]提出了不考虑土性、固结类型、动载类型、频率等因素影响的互相关函数法，计算土的阻尼比。

常规的土阻尼比的计算方法没有考虑参数频率的影响，但在随机荷载作用下土的阻尼比是与频率相关的，而此方面的研究较少，因此有必要在此方面展开研究。本文将随机过程理论引入土动力学特性测试与分析中，将动应力时程、动应变时程和动孔压时程均视为随机过程，在此基础上提出一种基于傅里叶变换的频域分析法，并通过试验及数值分析手段验证了利用该方法确定土的阻尼比的可行性。

2 土阻尼比确定的频域分析法

频域分析的傅里叶变换是将一般的时域函数x(t)转化成频域函数x(f)来进行研究的，其基本关系为：

(1)

(2)

其中x(f)为复变量，可以写成：

x(f)=|x(f)|ejφ(f)

(3)

式中： |x(f)|为x(f)的模;φ(f)为x(f)的相角;x(f)为信号x(t)的频谱。

随机过程理论将动载试验所得的动应力时程、动应变时程和动孔压时程均视为随机过程。试验测试和分析出的动应力功率谱用Gxx(f)来表示，动应变功率谱用Gyy(f)来表示，其互功率谱用Gxy(f)表示。用互功率谱定义的传递函数表示为：

H(f)=Gxy(f)/Gxx(f)

=|H(f)|e-jφ(f)=A(f)-jB(f)

(4)

(5)

(6)

式中： |H(f)|为传递函数H(f)的模；φ(f)为其相位角。

公式(6)表明，输出动应变和输入动应力的相位角φ(f)在物理意义上即为动应变滞后动应力的相角，反映了土的阻尼特性。

使用频域分析法进行地震荷载下土的阻尼比求解的具体流程为：

(1)采用Matlab编程对原始时间信号(输入信号x(t)、输出信号y(t))进行自相关函数Rx(τ)、Ry(τ)和互相关函数Rxy(τ)求解；

(2)对自相关函数、互相关函数进行如公式(1)傅里叶变换求得自功率谱Gxx(f)、Gyy(f)，对互相关函数进行快速傅里叶变换求得互功率谱Gxy(f)；

(3)由公式(4)表示出传递函数H(f)，然后进一步利用公式(6)求出输出动应变和输入动应力的相位差φ(f)；

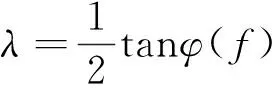
3 试验概况

3.1 试样制备

试验所用土样为取自某地铁现场的砂性土。土样的基本物理特性指标参数见表1。试样尺寸为100 mm(高)×50 mm(直径)，见图1。重塑土样的制备方法为水中落砂法。

图1 重塑砂样

3.2 试验过程

采用长安大学GDS空心圆柱扭剪试验系统的动三轴模块进行试验。

地震荷载作用下砂土的动三轴试验分为固结、动载两个阶段。固结阶段的固结应力比K(K=σ1/σ3)分别为1、1.5、2，固结围压分别为100、200、300 kPa，固结过程中当孔压消散为0且保持不变时固结完成；动载阶段的振动波形为埃而森特罗波(EL Centro)南北方向的地震波，历时为40 s，其中σd max分别为20、40、60、80、120 kPa。试验操作和数据整理均依据《土工试验规程》(SL237-1999)的步骤进行。

4 试验结果与分析

通过试验所得的EL Centro地震波的动应力时程曲线和动应变时程曲线分别如图2、3所示。

由图2、3可以看出动应力达到试验的设定值，动应变的发展趋势与动应力的基本相同；在荷载加载到20 s时动应变开始向负方向发展，这是与地震波的类型、动应力的幅值、固结围压等因素相关的。因为在均压固结的情况下，当较大的动应力幅值出现的时间比较早时，土样在拉伸阶段较大的固结围压导致试样产生较大的拉伸形变，故在接下来小的动应力幅值下会产生更大的拉伸形变，均压固结情况下，固结围压越大，轴向动应力幅值越大，则这种现象越明显；由于是均压固结，所得的动应力时程曲线和动应变时程曲线均可看做是平稳的时间过程。

在基于傅里叶变换的地震荷载作用下土的阻尼比的确定过程中采用Matlab编程对土的阻尼比进行求解，可得到阻尼比λ与频率f之间的关系如图4所示。

表1 土样的基本物理参数

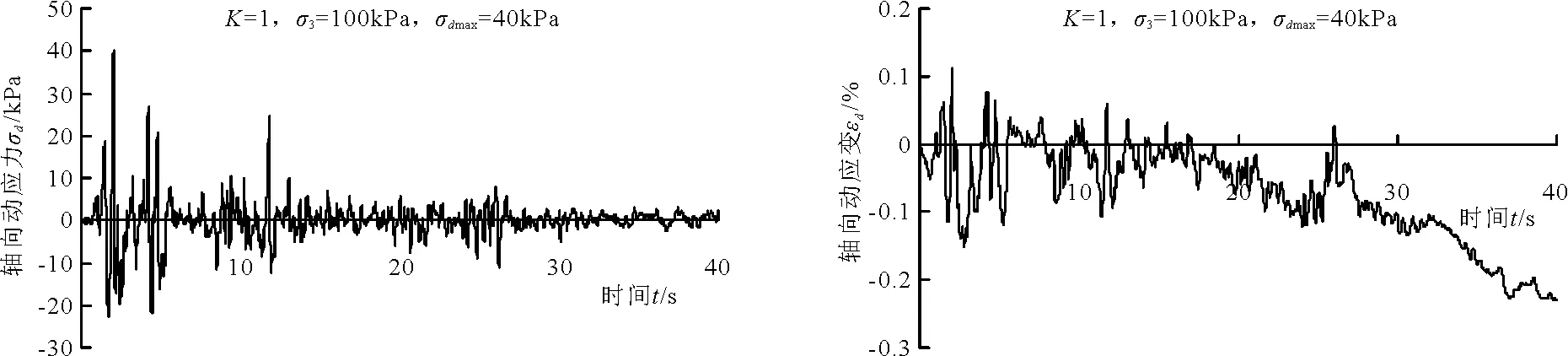
图2动应力时程曲线图3动应变时程曲线

图4 阻尼比λ与频率f的关系曲线

由图4可以看出，阻尼比不是确定值，而是随着频率的变化不断变化。在频率很小时，阻尼比受频率影响的波动较大；当频率逐渐增大，阻尼比受频率影响的波动较小，并逐渐减小。当固结围压相同时，随着固结应力比的增大，阻尼比随频率的波动情况在减弱；当固结应力比相同时，随着固结围压的增大，阻尼比随频率的波动也逐渐减弱。

(7)

动应变εd为动载时间段统计的动应变时程曲线的标准差，具体的计算公式为：

(8)

图5 阻尼比与动应变εd的关系曲线

5 结 论

将随机过程理论引入土动力阻尼比的确定过程中，将动应力时程、动应变时程和动孔压时程均视为随机过程。提出了一种基于傅里叶变换的频域分析法，并通过试验及数值分析手段验证了利用该方法确定土的阻尼比的可行性。有如下结论：

(1)采用基于傅里叶变换的频域分析法得到地震荷载作用下土的阻尼比λ是关于频率f的函数。任意一种土及地震波均可得到一条“阻尼比-频率谱”。

(3)工程应用上，建议将土阻尼比看作随地震波输入过程而动态变化的参数。只要通过频域分析法找到每类土、每种地震波作用下的“阻尼比-频率谱”，即可真正实现阻尼比参数的动态输入。并以此来考虑随机动荷载效应对土动力特性参数的影响。