初中数学常见最短距离问题及解法

余 立

（广东省广州市越秀外国语学校，广东 广州）

初中数学中，几何最短距离问题一直是重点题型之一，主要考查学生的综合运用能力，现以近几年常见的试题为例，介绍一些常用的方法。

一、利用“两点之间，线段最短”求最值

例题1：如图1，已知A、B两点在直线l同侧，在直线l上找一点P，使得PA+PB最小。

解：作点A关于直线l的对称点A′，连接A′B交直线l于点P，则点P即为所求的点（如图2）。

图1

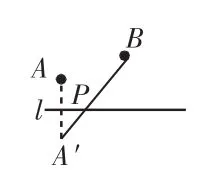
图2

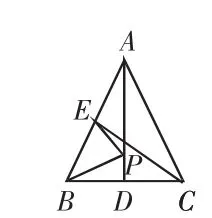
图3

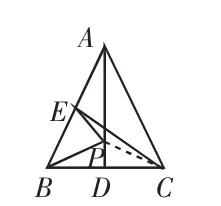
图4

几何最值问题通常为最短路线问题的引申，会与三角形、正方形、圆等图形结合，通过几何变换，找到关于动点所在直线的对称点，运用数形结合思想解决问题，这类题解答的关键在于“平面内两点之间线段最短”这一基本原理。

例题2：如图3，在△ABC中，AB=AC，AD、CE是△ABC的两条中线，P是AD上一个动点，则哪条线段的长度等于BP+EP最小值？

解：连接 PC（如图 4），

∵AB=AC，BD=CD

∴AD⊥BC

∴PB=PC

∴PB+PE=PC+PE

∵PE+PC≥CE

∴P、C、E共线时，PB+PE的值最小，最小值为CE的长度。

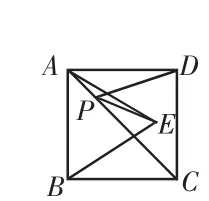
图5

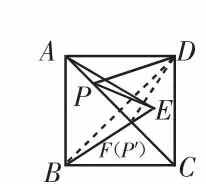
图6

例题3：如图5所示，正方形ABCD的面积为12，△ABE是等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，求PD+PE的最小值。

解：设 BE 与 AC 相交于点F（P′），连接BD（如图6）；

∵点B与点D关于AC对称

∴P′D=P′B

∴P′D+P′E=P′B+P′E=BE 最小

即P在AC与BE交点处时，PD+PE最小，为BE的长度。

∵正方形ABCD的面积为12

∵△ABE是等边三角形

由以上例题可知，解决这类最值问题，要认识到动点所在直线为对称轴，轴对称的作用在于改变点的位置关系，利用轴对称的性质和两点之间线段最短解决问题。当所求最小距离的两个点不在同一平面内时，则需要通过将曲面进行铺平处理，先求平面展开图，将曲面问题转换为平面问题。

图7

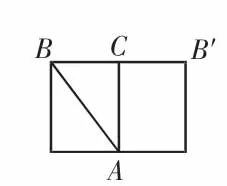
图8

例题4：如图7，圆柱的底面周长是14，圆柱高为24，一只蚂蚁如果要沿着圆柱的表面从下底面点A爬到与之相对的上底面点B，需要爬行的最短距离是多少？

解：将此圆柱展成平面图（如图8）得：AB即为所求。

∵圆柱底面周长为14，高为24，

即 BB′=14，AC=24

例题5：如图9是长为5，宽为4，高为3的长方体，一只蚂蚁从顶点A沿长方体的表面爬行到顶点B的最短距离是多少？

【分析】：A、B在同一平面，长方体展开图有三种可能（如图10），然后分别求出AB的长度，比较大小即可求得最短路程。

图9

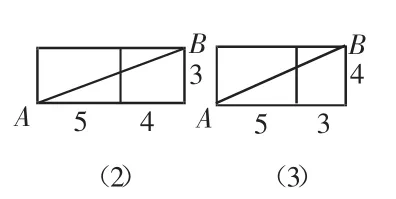
图10

二、利用“垂线段最短”求最值

例题6：如图11，在四边形ABCD中，∠B=∠C=90°，AB＞CD，AD=AB+CD；

（1）利用尺规作∠ADC的平分线DE，交BC于点E，连接AE（保留作图痕迹，不写作法）；

图11

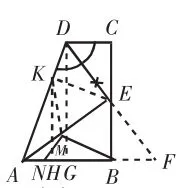
图12

（2）在（1）的条件下，

①证明：AE⊥DE；

②若CD=2，AB=4，点M，N分别是AE，AB上的动点，求BM+MN的最小值。

【分析】：②作点B关于AE的对称点K，连接EK，作 KH⊥AB 于 H，连接 MK；由 MB=MK，推出MB+MN=KM+MN，根据垂线段最短可知：当K、M、N共线，且与KH重合时，KM+MN的值最小，最小值为KH的长（如图12）。

例题7：如图13，矩形ABCD的对角线AC，BD相交于点O，△COD关于CD的对称图形为△CED；连接AE，若AB=6cm，

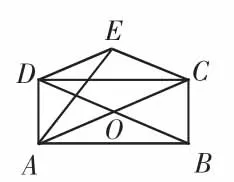
图13

求：①求sin∠EAD的值；

②若点P为线段AE上一动点（不与点A重合），连接OP，一动点Q从点O出发，以1cm/s的速度沿线段OP匀速运动到点P，再以1.5 cm/s的速度沿线段PA匀速运动到点A，到达点A后停止运动，当点Q沿上述路线运动到点A所需要的时间最短时，求AP的长和点Q走完全程所需的时间。

【分析】：②作 PF⊥AD 于F，已知 PF=AP·sin点Q的运动时间当 O、P、F 共线且PF⊥AD时，OP+PF最短。

综上所述，利用图形变化解决最短途径问题，基本解题思路是在不改变线段长度的前提下，运用对称变化把对称轴同侧的两条线段转化为对称轴的两侧，根据“两点之间线段最短”或“垂线段最短”原理，把“折线”转“直”，找出最短位置，求出最小值。