电离层延迟及其特性的公式推导
周晓慧,黄劲松,徐晓华,郭斐
(武汉大学 测绘学院,湖北 武汉 430079)
0 引 言
电离层延迟是影响GNSS导航定位精度的重要因素,尤其是对于理解“到底是测距码测短了,还是载波测长了?”这样的问题,在本科教学过程中,教师较易出现难以解释清楚,学生容易出现无法接受既成事实的现象.本文从载波、测距码信号的本质出发,通过较为严密的公式推导,回答上述问题,并且为本科教学电离层延迟及其特点提供一种讲解思路,供同行参考.
1 基本概念
1.1 相位的概念
GNSS的信号是由测距码和导航电文调制后依附在正弦波形式的载波上从卫星端播发的.单一的信号在播发的过程中,通常用正弦波/余弦波,如图1所示,在时间域内进行描述,其数学表达式为
y=Acos(ωt+φ).
(1)
式中:A为振幅;ω=2πf是角频率;φ为初相;t为某一时刻. 而相位的定义是某一时刻波上点的位置,对应的图1中黑点的位置.
1.2 相速度及其计算
相速度,是指相位在空间中传播的速度.因此,需要在空间域内描述信号,可采用波动方程表示为
ξ=Acos(ωt-kx).
(2)
式中:ω含义同式(1);k=2π/λ,称为波数;(ωt-kx)为相位. 对应于图2中的实心原点与空心圆点两点,分别对应的是不同时刻的相位.
根据相速度的定义,选择波动方程中的任意相位(ωt-kx)=c,如图2中菱形点所示,可以得到其从t1到t2时刻的传播距离为dx,相应地,相速度可以表示为
(3)
而(ωt-kx)=c,对时间求导:
(4)
整理可得,
(5)
结合相速度及角频率定义,可得相速度的表达式为
(6)
可见,单一的电磁波在媒介中传播是波长和频率的函数.
1.3 合成波及包络的概念
GNSS信号由测距码、导航电文和载波组合而成,如图3所示,可以看作是一种组合波.采用最简单的两个余弦波合成为例,来讲解合成波及包络的概念.
假设分别有2个单一的正弦/余弦波,其波动方程可以分别写作
ξ1=Acos(ω1t-k1x),
ξ2=Acos(ω2t-k2x),
(7)
式中,ω1、ω2、k1、k2含义同式(3). 利用三角公式的和差化积,可得到合成波的表达式:
ξcom=ξ1+ξ2
(8)
实曲线中相邻波峰波谷的虚线即为包含着高频信号的低频曲线,也是常说的包络线,它是能量传播的基本单元,如图4所示.
1.4 群速度及其计算
GNSS载波信号是以合成波的形式传播的,因此,通过包络在空间传播的速度来进行描述,即群速度是包络的相速度.根据1.3节内容,包络方程为
(9)
与相速度推导过程相似,群速度可写作
(10)
2 电离层传播距离计算
2.1 相、群速度之间的关系
结合式(7)、(10)及波数的定义,可得相、群速度之间的关系为
(11)
2.2 相、群折射率之间的关系
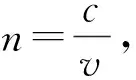
(12)
结合式(12)和式(13)可得,
(13)
又因ε为小数时,(1+ε)-1=1-ε,顾及λ=c/f,可得相、群折射系数之间的关系:
(14)
对于GNSS信号而言,截断的电离层折射系数是频率f的函数:
(15)
式中:Ne为电子密度;qe和me分别为电子电荷和质量,将其代入式(14)和式(15),分别可得
(16)
2.3 电离层中信号传播距离
信号在电离层中的传播时间为
(17)
信号在电离层中传播的距离为
(18)
此式即著名的依据Fernet’s定理.
3 电离层延迟计算及其特性
3.1 GNSS测距基本思想
GNSS通过距离交会实现定位、导航和授时的主要功能.距离交会可通过测距码或载波进行距离测量实现,其基本思想是获得信号传播时间,乘以速度.而在接收机内部,通常采用光速作为信号的传播速度,即
S0=c×t.
(19)
式中:S0为理论计算的信号传播距离;c为光速;t为信号的传播时间.
3.2 电离层延迟的计算及特性
(20)
对测距码和载波而言,结合式(16)、(18)和式(20),它们对应的电离层延迟分别为
(21)
即,
(22)
因此公式(22)可写作:
(23)
从式(23)不难看出,电离层具有以下特性:1)电离层延迟大小与总电子含量成正比;2)电离层延迟大小与频率的平方成反比;3)码伪距和载波相位受到的电离层延迟大小相等,符号相反.
4 结束语
GNSS原理相关课程已成为众多开展大地测量、工程测量等方向的核心课程,作为影响定位效果的误差源-电离层,它对测距码和载波信号造成的测距误差出现大小相等、方向相反的结论一直未能较好地给予形象解释.本文试图从GNSS信号的本质出发,通过较为严密的公式推导,证明了相应的结论.

