一题多解拓展视角,弃“量”从“精”提升能力*
——以一道证明线段相等的几何题为例
☉福建省厦门大学附属实验中学 林运来
☉福建省泉州市丰泽区教育局 周玉宝
一、问题提出
培养中小学生智力灵活性最简单的办法就是求多解的练习.以一题多解为例,从各种规律中找出规律,便能举一反三,比盲目多做题的效果要好得多[1].习题教学切不可就题论题,“一解而过”,而要引导学生从不同视角进行深度探究,充分挖掘习题背后隐性的价值和内涵,拓展学生数学思考的视角,提升学生的数学能力.因此,如何弃“量”从“精”,切实减轻学生过重的作业负担,全面提升学生分析问题的能力,便成为了习题教学的主旋律和一种高境界的追求[2].
习题教学就其目标而言,除了巩固知识,主要还是培养学生的解题能力和完善学生的思维方式[2].因此,习题教学中如何才能最大限度地提高课堂教学的有效性,让学生掌握数学知识的本质,领悟数学思想方法的精髓,提升数学思维品质,提高数学素养,的确是一个值得探索与急需解决的问题.数学对人的作用是以促进人的逻辑思维为首要的,而这一重要作用又与数学证明有着密切联系.笔者以一道“证明线段相等”的几何题为例开展一题多解训练,有一些心得体会,现写出来与大家交流,希望能抛砖引玉.
二、原题呈现
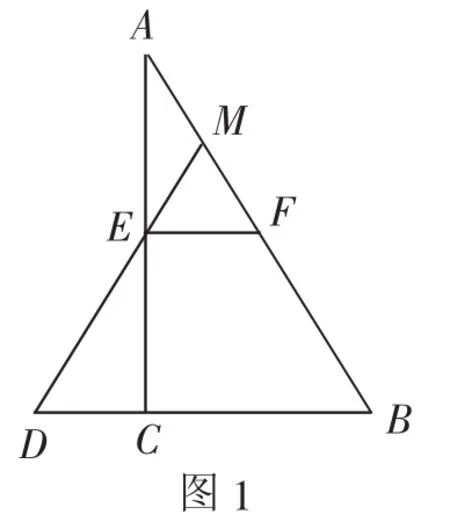
如图1,在Rt△ABC中,∠ACB=90°,点E、F分别是边AC、AB的中点,延长BC到点D,使2CD=BC,连接DE并延长交AF于点M.求证:点M是AF的中点.
三、教学片段呈现
[片段1】
师:从题目中你读出了哪几个条件?
生1:Rt△ABC,AE=CE,AF=BF,2CD=BC.
师:题目需要我们解决什么问题?
生2:证明点M是AF的中点.
师:这个问题还能怎样表示?
生3:证明AM=MF,或证明AF=2AM,或证明AF=2MF.
师:还有其他不同表示吗?
师:你能直观得出△AEF是什么三角形吗?
生5:直角三角形.
师:根据要证明的结论,我们可以选择组合方案“直角三角形AEF(已知可证)+M是AF的中点(结论)”,于是可以利用“直角三角形斜边上的中线等于斜边的一半”的逆定理进行证明.
思路1:利用“直角三角形斜边上的中线等于斜边的一半”的逆定理.
证法1:如图1,因为E、F分别是边AC、AB的中点,所以,即,所以,所以MD=3ME=ME+ED,则DE=2EM.
因为AE=EC,∠AEF=∠ECD=90°,EF=CD,所以△AEF △ECD,所以AF=DE=2EM.即M是AF的中点.
[片段2】
师:类比证法1的分析,你能提出解决问题的其他“已知+结论”的组合方案吗?
生6:选择组合方案“E是AC的中点(已知)+M是AF的中点(结论)”,可以利用三角形中位线定理的逆定理进行证明.
思路2:利用三角形中位线定理的逆定理.
证法2:如图2,连接CF.
因为E、F分别是边AC、AB的中点,所以EF∥BC,且2EF=BC.
又因为2CD=BC,且B、C、D三点共线,所以EF∥DC,EF=DC.
所以四边形DCFE是平行四边形,则EM∥CF.因为E为AC的中点,所以M是AF的中点.
[片段3】
师:有没有考虑使用条件“2CD=BC”的?
生7:根据已知“点F是AB的中点”,结合要证明的结论,我发现2MF=BF,于是选择组合“2CD=BC(已知)+2MF=BF(结论转化)”,可以利用平行线分线段成比例定理进行证明.
生8:根据已知涉及线段中点较多,考虑延长CD到点G,使得CD=DG,可知“D为CG的中点,C为BG的中点”,刚好与“M为AF的中点,F为AB的中点”对应,于是可以利用平行线分线段成比例定理的逆定理进行证明.
思路3:利用平行线分线段成比例定理.
证明3:如图2,连接CF.
因为E、F分别是边AC、AB的中点,所以EF∥BC,且2EF=DC.
又因为2CD=BC,且B、C、D三点共线,所以EF∥DC,EF=DC.
所以四边形DCFE是平行四边形,所以DM∥CF.
所以M是AF的中点.
思路4:利用平行线分线段成比例定理的逆定理.
证明4:如图3,延长CD到点G,使得DG=CD,连接AG、CF.
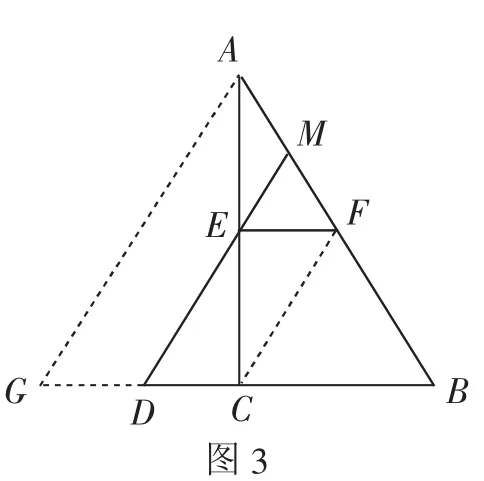
因为D、E分别是CG、CA的中点,所以DE∥AG,即DM∥AG.
因为C、F分别是BG、BA的中点,所以CF∥AG.
所以CF∥DM∥AG.
因为D为GC的中点,所以M是AF的中点.
[片段4】
师:以上几种证明思路都非常棒!利用了直角三角形的性质、三角形的中位线、平行线的相关结论解决问题,解题思路稳中求胜.
师:问题涉及直角三角形,即有直线与直线垂直,还可以从什么角度进行探索?
(教师从另外一个角度提出问题,旨在引导学生再次进入新的探究活动中)
生9:还可以构造相似三角形,利用对应边成比例进行证明.
生10:还可以“戴上笛卡尔眼镜”,通过建立直角坐标系,利用代数方法“以算代证”.
(生10把教师平常教学中常说的话惟妙惟肖地演绎出来,全班同学不禁会心一笑)
思路5:利用相似三角形的性质.
证明5:如图4,作MH⊥BC,垂足为H.
由已知得MH∥AC,所以△BMH △BAC,△DCE△DHM.

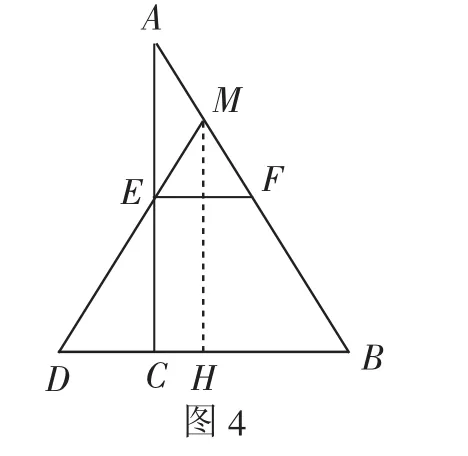
所以M是AF的中点.
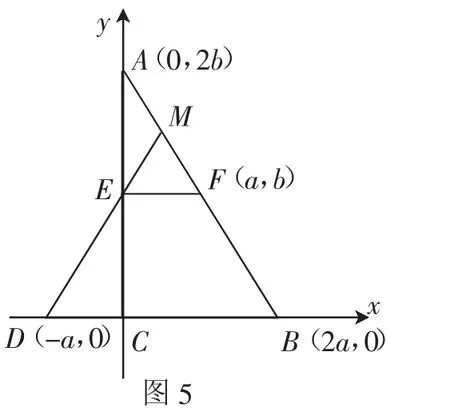
思路6:利用中点坐标公式.
证明6:如图5,以C为坐标原点,以CB为x轴,建立平面直角坐标系xOy. 设点A(0,2b)、B(2a,0),则点D(-a,0)、E(0,b)、F(a,b).

四、写在最后
1.解题教学要引导学生打通问题的条件与结论之间的“通道”
美国著名教育心理学家奥苏伯尔曾经说过:“假如让我把全部教育心理学仅仅归纳为一条原理的话,那么,我将一言以蔽之曰:影响学习的唯一最重要的因素,就是学习者已经知道了什么,要探明这一点,并应据此进行教学.”[4]当面对一个新问题时,教师要引导学生明确思考方向,通过联想问题的结论与已经学过的相关内容之间的联系,并对这种联系加以认真思考,打通问题的条件和结论之间的“通道”,由此找到解决问题的思路和方法.
当然,以上几种解题思路并没有穷尽问题的思考方法,重要的是,以上不同解法涉及了几何中许多重要的定理,覆盖了多个几何知识点,多进行这样的解题训练,有助于减轻学生的学习负担,使学生学会梳理几何知识间的因果关系,了解需要理解哪些数学知识才能更好地解决任务,培养学生的逻辑思维能力,提高几何思维水平,进而培养学生的探索精神和创新能力.
2.解题教学应促进学生深度思考
良好的数学教育是促进学生可持续发展的教育.在解题教学中,要从不同的认识层次、观察角度、知识背景和问题特点出发进行一题多解、一题多变[1].一题多解有助于培养学生深度思考的能力和发散性思维.这里的一题多解就是基本活动经验,相同的方法就是数学的思想方法,数学思想方法是在基本活动经验中累积和提升的[3].面对一题多解,既要多解归一、揭示实质,也要比较优逆势、择善而从.笔者让学生课后整理题目的不同解法、并对解法进行评鉴,既有助于学生把握解题实质,又培养了学生的辩证思维和选择能力.
解题教学要培养学生的深度思考能力,教师要克服将知识“大餐”端上来而不讲烹饪方法的倾向,要站在知识体系的高度去思考,善于发现和揭示问题的本质规律,结合具体问题将学科知识融会贯通、刨根问底,结合学生实际,对问题的深入思考与拓展做到自然而然、深入浅出,以问题为载体引导学生不断思考、不断优化,不断给学生以点点滴滴的思维启迪,培养学生的知识迁移能力,以及善于研究、实证的精神,培养和提升学生解决问题的能力,使学生成为学习的主人.真正将教师“教案中的方法”变成学生“头脑中的智慧”.

