浮绳式围网水动力特性研究

崔 勇，关长涛，黄 滨，贾玉东

(农业部海洋渔业可持续发展重点实验室，青岛市海水鱼类种子工程与生物技术重点实验室，中国水产科学研究院黄海水产研究所，山东 青岛 266071)

中国海洋资源丰富，离岸海域大多未经开发，而海水养殖由近岸向离岸深远海区域拓展成为“十三五”渔业发展的重要方向。离岸大型围网作为一种新型养殖模式，相对于传统的网箱养殖，可有效利用海域的饵料生物，促进鱼类摄食平衡；同时，依托围网设施建立鱼、贝及藻类的立体混养系统可起到净化周围海域环境、降低养殖污染的作用[1]。离岸大型围网设施可布置于开阔水域，由于围网结构规格较大，受到海水潮汐、风浪等作用明显。通过开展围网水动力特性研究，可为其设计选型、海上安装等提供依据。

目前，国内已建立的大型围网设施主要分为柱桩式、堤坝式、网格式与浮绳式等，网衣材料多采用聚乙烯或铜合金。石建高[2-3]开展了多种围网设施的系统研究，实现了超高分子量聚乙烯网衣、铜合金网衣等新型网衣材料在大型围网设施上的应用，获发明专利多项；王磊等[4]分析了柱桩式铜合金围网养殖设施的发展现状；桂福坤等[5]对一种桩柱式围网网片的波浪力学特性开展研究，着重分析了不同网片尺度和固定方式下单元网片的网线张力分布、结节偏移和桩柱系缚点受力特性；陈天华等[6]采用集中质量点法和网目群化法，结合数值模拟技术探讨桩柱式围网网片单元在水流作用下的力学特性；叶卫富等[7]结合实际生产需要，设计模型水槽试验，开发出适宜于水深5～10 m的养殖浮绳式围网设施。

本研究以布设于莱州湾海域的一种大型浮绳式围网为研究对象，通过水池模型拖曳试验，以及基于有限元分析软件提供的参数化建模技术，对其在波流作用下的水动力特性进行研究，研究结果可为浮绳式围网工程设计提供理论参考。

1 材料与方法

1.1 试验设备

围网模型试验在中国水产科学研究院东海水产研究所网具模型试验水池进行。试验静水池主尺度90 m×6 m×3 m；拖车拖速0.1～4.0 m/s，相对精度P≤0.1%；测力系统使用自行研制的经防水处理后的LH-S02微型力传感器，量程0～20 kg，测力仪器的线性误差小于满量程的0.5‰；利用ROV水下摄影机获取网衣变形情况[8]。

1.2 围网原型及模型规格参数

浮绳式围网原型规格为长100 m×宽50 m，网片选用聚乙烯材料，网目尺寸60 mm，网线直径6 mm。网片为L型，立网20 m，底网2.5 m，立网底部与木桩绳子连接固定于海底。泡沫浮子固定在上口网纲上，浮子规格直径500 mm×长900 mm，共333个浮子可提供59 t浮力(图1)。围网模型选用大尺度比λ为50、小尺度比λ′为2进行制作。网衣材料为PE经编网，网目尺寸30 mm，网线直径3 mm。上纲总长6 m，由直径6 mm PE绳穿80个直径46 mm×长60 mm的圆柱形泡沫塑料浮子构成，实物网具设计配备浮力换算为模型为77 N。下纲与直径20 mm不锈钢管焊接成的矩形框(2 m×1 m)按缩结系数均匀绕结而成。

图1 浮绳式围网现场图

1.3 试验方法

根据渔具模型试验准则1(田内准则)进行[9-11]。浮绳式围网模型上纲可自由变形，下纲绕结于不锈钢矩形框。试验时固定不锈钢矩形框于导流杆，固结点为水面下0.4 m，上纲上取迎流面矩形直角对应上纲的2点各作为测力点，测力传感器固定于拖杆与上纲两角之间，测力方向与运动方向平行，试验连接见图2。

根据运动转换定律，拖车车速等同于水流速度。模型试验速度分别为0.18、0.36、0.55、0.73和0.91 m/s，对应实际流速为0.26、0.51、0.77、1.02和1.28 m/s。围网阻力的测试通过LH-S02微型力传感器进行采集，由电脑软件读取。测力试验分别针对围网迎流面边长为1 m和2 m两种情况下进行。

图2 模型试验布置图

1.4 数值模拟

根据有限元动力分析方法，浮绳式围网整体结构在波流场中的运动可由公式(1)表示[12]：

(1)

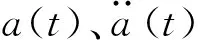
F(t)和R(t)分别是流体静载荷和动载荷效应引起的等效节点力矢量。

围网主要由浮子与柔性的网衣组成，围网结构离散后形成不同的结构单元，首先获取不同特性单元的质量矩阵、刚度矩阵和节点力矢量，然后组装形成围网总体结构的质量矩阵、刚度矩阵和节点力矢量。

围网离散后的浮子单元用管单元来模拟，其单元质量矩阵形式与三维梁单元相似[13]，其中，

(2)

(3)

式中：A、I分别为单元的横截面积和惯性矩；D、d分别为单元的外径和内径；围网离散后的网衣和锚绳单元用管单元模拟时，仅考虑单元轴向拉伸效应，单元内径d设置为0，其单元的刚度矩阵与质量矩阵与三维杆单元相同。单元载荷通过Morison方程计算[14-15]：

(4)

通过有限元软件力学计算模块内置的管单元模拟离散单元[16]。管单元可模拟拉、压、弯作用，并且能够模拟受海洋波流作用下的单轴单元，可以用来计算位于水中的圆管形构件的浮力、波流力的静载荷与动载荷，其中对于围网浮子系统可简化为管单元来模拟。如果单元位于水中，其水动力载荷自动施加；如果单元位于水面以上，则只有重力载荷。因此，数值模型可针对结构单元的位置对其水动力进行自动调节。

2 结果与讨论

2.1 围网水阻力

图3为当迎流面分别为长边(L)和宽边(W)两种条件下，在试验流速范围内，围网实物整体阻力随流速变化的关系曲线。由图可知，围网整体阻力与流速呈幂函数关系，其回归函数分别为：

FL=35.69v2.031 4，相关系数R=0.997 6

(5)

FW=29.16v2.079 7，相关系数R=0.997 6

(6)

式中：FL、FW为围网迎流面分别为长边和宽边两种条件下的整体阻力，kN；v为相对流速，kn。

从图3可以看出，在相同流速下，当迎流面为长边时的围网总阻力均大于迎流面为宽边时，这是由于迎流面为长边时围网阻流面积较大所致。当迎流面为宽边时，在0.26～1.28 m/s的流速范围内，围网的阻力由6 900 N增加到196 060 N，增加了约27倍。

图3 围网阻力随流速变化

2.2 围网变形

在试验拖速下，利用ROV水下摄影机可见，当迎流面长度为1 m、拖速为0.51 m/s时，所有的浮子可浮于水面上方。随着拖速的上升，迎流面网片在水平方向弯曲成弧形，在垂直方向也呈弯曲状。随着拖速的增加，网片弯曲程度有所加剧，浮绳式围网的网衣高度逐渐缩小，浮子向水面下降。当拖速达到1.02 m/s时，与拖曳方向垂直的迎流面网衣上的浮子均下降至水面以下，前侧下降的幅度强于后侧，但侧面的浮子未见沉于水面以下(图4)。就网形而言，由于下纲形状固定，上纲由多点系泊，围网受流后网片从中间弯曲，从而使网衣的有效高度下降。

图4 围网变形水下观察

2.3 波浪作用仿真结果

利用有限元方法建立围网结构的数值模型，模型具体参数与水池试验模型一致。围网结构采用四点锚泊法，迎波面边长1 m，测边2 m，网衣高度0.4 m。为提高计算效率，网衣系统采用网目群化方法[17-18]。波浪工况取波高为9 cm，周期1 s为例进行计算[19-20]。图5为波浪作用下第5秒的围网瞬时变形情况。计算机模拟的结果显示，围网的浮子与网衣系统随着波浪作周期性的往复运动。

为比较不同位置的浮子运动幅度，选取围网上纲四角与四边中点处的浮子，顺序按逆时针方向依次编号为1～8(图5)。图6为不同位置处浮子的最大横向位移和纵向位移比较值。从图6可以看出，浮子的最大横向位移出现在迎波面两边的中点处，而两侧边中点处的浮子横向位移最小。此外，与锚绳相连的四角处的浮子最大横向位移介于前两者之间。在纵向位移比较中，各点浮子的最大位移值差距不大，上纲四角处的浮子略大于迎波面两边中点处，而两侧边中点处浮子的纵向位移依旧为最小。从图中还可以看出，除了迎波面两边中点外，其余6个位置点浮子的纵向位移均大于横向位移。由此可见，浮子在波浪作用下的运动较单纯水流作用下更为复杂。

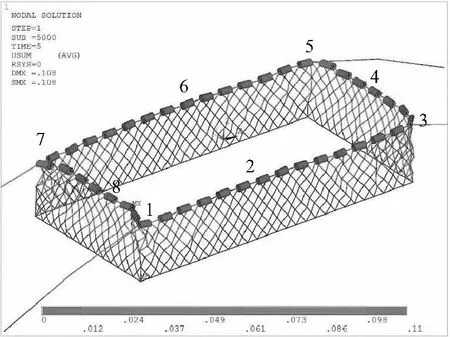
图5 波浪作用下围网变形

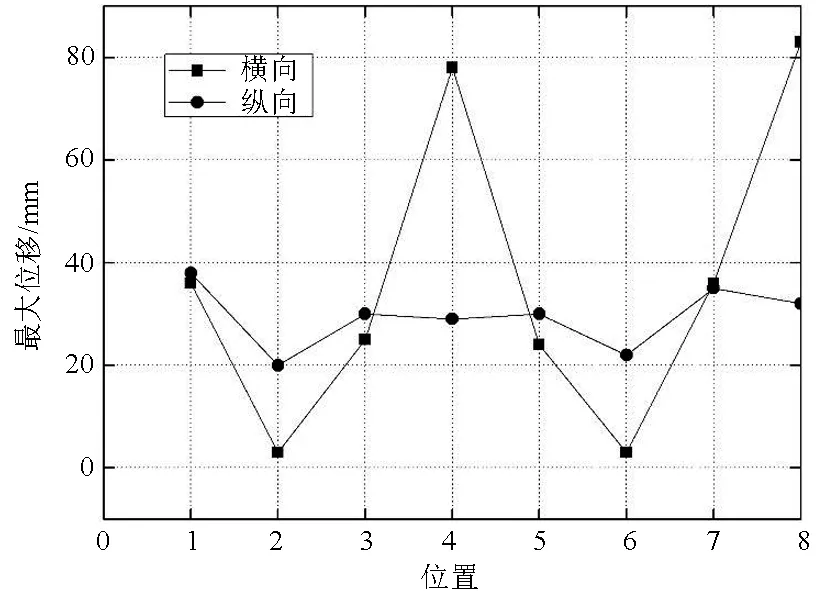
图6 不同位置浮子运动幅度比较

图7为不同位置处围网上纲与下纲网衣连接点网线的最大张力，其中下纲所选取1～8点位置与上纲垂直对应。从图中可以看出，不同位置处网衣网线的最大张力差别较大。上纲各点中编号1、3、5、7点与锚绳相连接处网线的张力明显大于其它位置点处。下纲中与网底固定的四角连接处的网线张力为最大。在上纲与下纲中，编号2、6代表的与波浪顺向的侧边中点处连接的网线张力值为最小。文献[5]对桩柱式围网网片的波浪力学特性研究中，发现网片与桩柱的系缚点最大受力出现在上端点，其次是下端点，且数值上均远远大于桩柱中间的系缚点，此结果与本文的计算结果基本一致。此外，由图中还可看出，在1、3、5、7四角处的位置点，与上纲连接的网线张力要小于与下纲连接的网线张力。

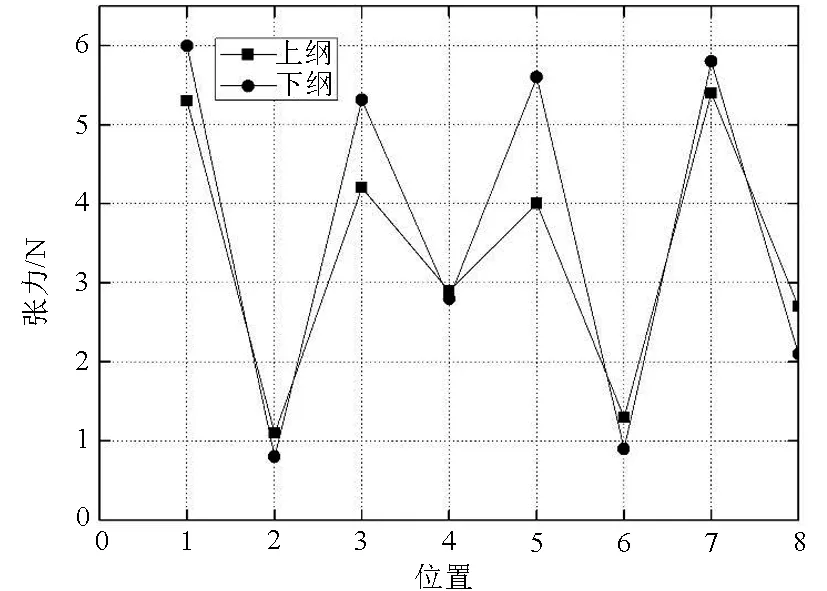
图7 不同位置网线最大张力比较

3 结论

浮绳式围网主体由网片和浮子组成，由浮子提供浮力来使网衣展开，网衣所包围区域可为鱼类提供生长空间。从围网结构组成可以看出，此类结构整体的柔性比较大，当围网设施布置于开阔海域时，受波浪与海流作用的影响比较大，因此，确保整个围网系统的稳定性十分重要。通过水池模型试验，研究了围网实物阻力与流速变化的关系，得出围网整体阻力与流速呈幂函数关系。研究发现，围网整体阻力与其迎流面积相关。随着流速上升，迎流面的浮子下降于水面下方，浮力不足明显。建议适当增加迎流面网衣所配备的浮力，以使围网在较高流速时能够保持一定的网形。当浮绳式围网在波浪作用下，上纲中迎浪面中点处浮子的位移最大，而顺浪侧浮子的位移较小。在网衣张力模拟中，发现网片与锚绳连接点及下纲四角连接处的网线张力较大，因此在实物网衣的制作中，此处的网衣应做加固处理。此外，有关锚泊方式对浮绳式围网水动力学特性的影响也十分重要，今后将进一步开展研究。

□