流媒体系统中内容分发网络的服务器部署优化
徐锡健,邬惠峰,吴海列
(杭州电子科技大学 计算机学院,浙江 杭州 310018)
0 引 言
近年来随着流媒体的应用和普及,如何保证用户体验及降低成本成了研究热点。袁小群等[1]提出并分析了服务器优化部署对流媒体系统的重要性。
内容分发网络(content delivery network,CDN)被广泛应用到流媒体的内容分发研究中。CDN网络中服务器的放置至关重要,曾明霏等[2]就P2P服务器如何放置以满足尽量多节点进行了研究,郑晶晶等[3,4]分别提出分布式交互应用中服务器放置问题的模拟退火、禁忌搜索和改进遗传算法的解决方案。此外,Hamid Jabraili等[5,6]也研究了服务器部署中提高延时性能,优化服务质量的启发式算法。Darothi Sarkar等[7,8]调查了多种CDN网络中副本服务器的放置算法并概括了他们的特点。时延性能是他们的主要研究问题,但是在流媒体CDN中,带宽保证比时延更重要,只要能保证分发给用户的流内容最低吞吐量,流媒体播放器的缓冲机制就能控制延迟抖动在一个有界范围内,从而保证用户体验[9]。同时考虑时延性能和带宽约束的数学模型太过复杂,不易处理,本文建立了考虑服务器部署成本、网络租用成本、带宽约束和用户流量需求的MCMF(minimum cost maximum flow)模型[10],并用模拟退火遗传算法求解该模型,同时与文献[10]中该问题的混合整数规划模型求解结果进行了比较,确定了算法的可行性和有效性。
1 数学模型
1.1 问题描述
流媒体内容服务器部署问题可以描述为:在给定的网络拓扑图中,有N个网络节点,其中有M个消费节点。从网络结构模型中选择一部分网络节点,在其上一对一的部署流媒体内容服务器。提供的部署方案需要使得媒体流从内容服务器经过一些网络节点和链路到达消费节点。两个网络节点之间最多仅存在一条链路,每条链路有相应的带宽限制和单位带宽租用费,求满足所有消费节点的流量需求下总成本最低的服务器部署方案。
1.2 符号说明
设G=(V,E)为赋权图,V={0,1,2,…,N-1},{v0,v1,…,vn-1}为顶点集,E={e1,e2,…,en}为边集,xi-j为节点vi和vj之间的链路总带宽,wi-j为该链路的单位带宽租用费,fi-j为从i到j的流量,每个服务器的部署成本是cost。为了符合MCMF模型,需要在图上添加一个虚拟源节点和一个虚拟汇节点,源节点序号为N,与所有服务器节点相连,假设所有流量都从源节点输出;汇节点序号为N+1,与所有消费节点相连,假设所有流量最终都传输到汇节点,设V’={0,1,2,…,N+1}{v0,v1,…,vn+1}为包含源汇节点的顶点集,以源节点和汇节点为端点的链路带宽无限制,网络租用费为0。对于第i个节点,设
(1)
设有M个消费节点的集合为VU={vu1,vu2,…vuM},其中VU⊆V,每个消费节点的需求是NE={nu1,nu2,…,nuM}。
1.3 目标函数及约束条件
本文综合考虑服务器部署成本,网络租用费,链路带宽限制,用户流量需求,如下双目标规划模型
(2)
(3)
其中,pi表示第i个节点是否是服务器节点,约束条件1说明这是一个二值项,cost为每部署一个服务器的成本,wi-j与fi-j的乘积是一条链路的实际网络租用费,条件2表示每条链路的实际流量不会超过该链路的流量上限,条件3表示每个消费节点的流量需求都恰好被满足,条件4表示除了源汇节点的其它节点的流量入度和初度总和是相等的,以此确保从服务器输出的流量能全部传输到消费节点。
原网络拓扑图的一个实例如图1所示:正方形代表服务器节点,三角形代表消费节点,圆圈代表普通节点,链路上的标记(x,y)中,x表示链路总带宽(单位为Gbps),y表示每Gbps的网络租用费(千元)。添加了源汇节点的网络拓扑图如图2所示,流量从源点S出发经过若干服务器节点,普通节点和消费节点最终到达汇点E。

图1 原网络拓扑图

图2 带源汇节点网络拓扑图
2 算法设计
2.1 算法描述
本文提出的问题是一个多目标优化问题,相对于单目标优化,多目标的主要特征是权衡各个目标使其达到综合的最优解,此类问题多采用启发式算法解决,本文采用自适应模拟退火遗传算法解决此问题。
2.1.1 遗传算法
遗传算法(genetic algorithm,GA)的定义请参见文献[11]。遗传算法的全局搜索能力强,但是存在早熟问题,详情请参见文献[12],需要进行优化,因此本文根据适应度的变化,自适应地变化种群交叉概率pc和变异概率pm,而适应度的集中程度用最大适应度fitmax、最小适应度fitmin和适应度平均值fitave这3个变量来衡量。可以利用如下公式对pc和pm进行自动调整
(4)
(5)
实验表明,本文的问题中a取0.78,b取0.66可以达到很好的效果。自适应遗传算法虽然运行效率上比改进前算法有了显著的提高,但其局部搜索能力还有改进空间。
2.1.2 模拟退火算法
模拟退火算法(simulated annealing)的定义及原理请参见文献[13]。模拟退火算法的局部搜索能力强,但对于基本的模拟退火算法,在问题规模很大时想要得到一个高度接近最优解的结果需要花费的时间过长。
2.1.3 模拟退火遗传算法
模拟退火遗传算法是在遗传算法的基础上引进模拟退火思想的一种改进算法,能有效避免两者的缺点,结合两者的优点。模拟退火遗传算法分内外两层,外层从一个较高温度开始逐渐下降,期间运行遗传算法,内层进行子种群的寻优,当温度到达下限或者连续若干代迭代的最优解一直没有变化时,算法结束。
2.1.4 SPFA算法
SPFA算法是一种对任意有向图求单源最短路径的算法,夏正冬等对其正确性和效率都有分析[14]。本文的图结构的链路中实际流量的流动方向是不确定的,因此若将一个方向作为正向,该边就是正权边,其反向边就是负权边,这时一些最短路径算法如Dijkstra算法等就无法处理了,而Bellman-Ford算法的复杂度过高,因此本文选用了SPFA算法。
2.2 算法实现
2.2.1 编码
遗传算法将实际问题抽象成染色体编码的方式进行求解,每一条染色体对应一个该问题的解决方案。遗传算法的编码方式有多种,本文采用二进制编码,一条染色体是一条0/1序列,分别对应非服务器节点和服务器节点两种情况,序列下标代表网络节点序号。
2.2.2 产生初始种群
初始种群是利用随机数函数生成若干条染色体组成的,种群规模跟网络节点个数存在一定联系,起初网络节点越多,种群规模越大,随着网络节点不断增多,计算单个染色体方案的路径搜索耗时急剧增加,此时需要减小种群规模以保持迭代速度。初始种群可表示为A={X1,X2,…,Xn},其中Xi是种群中的第i条染色体。
2.2.3 适应度函数设计
针对本文多目标优化求最小代价问题,代价越高,个体适应度越差,同时为了提高算法效率,将代价设置上界,当且仅当在所有消费节点都部署服务器时,代价达到可接受的最大值max,此时所有消费节点的流量需求都被满足,再增加一个服务器都是多余的,适应度函数构造如下

(6)
其中,P(x)为当前方案的代价。
2.2.4 选择
每次迭代需要从种群中挑选出适应度高的个体用以进行后续操作。本文采取的选择策略是锦标赛选择法,每次从种群中随机抽出两个个体,适应度较大者遗传到下一代,另一个个体以模拟退火的方式按一定的概率接受,这个概率为
(7)
式中:dE是适应度的变化量(负数),取该个体的适应度与fitmax的差值,与fitmax相差越小,表示该个体适应度较优,P(dE)越大,由于dE总是小于0,所以P(dE)取值在0到1之间。k为常数,T表示温度,为正数,设定初始值后,迭代过程中T按一定比率降低,算法初期温度高,P(dE)一般较大,保持种群多样性,后期温度低,P(dE)小表示种群靠近最优解邻域,逐渐稳定。
2.2.5 自适应交叉

2.2.6 自适应变异

模拟退火遗传算法的基本流程如图3所示。

图3 模拟退火遗传算法流程
2.3 MCMF模型与SPFA算法
遗传算法过程中计算个体适应度的时候需要根据服务器的分布状况确定网络中各节点间的流量大小和流向,使得网络租用费最小,这是一个MCMF问题,寻路过程中存在负权边,因此选用SPFA算法。
2.3.1 MCMF问题求解
MCMF问题是结合网络流的费用和流量问题,寻找最优解的问题[16],在一个网络的每段路径都受容量和费用限制的条件下,该模型试图计算出从一个点到另一个点的流量最大,费用最小的解决方案。本文中,MCMF的实现步骤如下:
步骤1 初始化图中所有边xi-xj之间的当前流为0,xi,xj为图中任意连通的两个点,初始化每条边的剩余流量带宽bw,费用流总代价totalCost和当前流大小为0。
步骤2 调用SPFA算法搜寻到一条从起始节点S到终止节点E的增广路径,按顺序记录路径上从S到E的网络节点{x0x1…xi…xj},若找不到增广路径,跳到步骤4。
步骤3 从步骤2中记录的路径中找出限制可行流大小的关键边xi-xi+1,若此边的当前流为负,则以此当前流的绝对值作为这条路径可行流的大小minf,否则,以此路段的剩余流量带宽bwi-(i+1)作为这个可行流的大小minf。修改残留网络信息并更新totalCost和currentFlow。
步骤4 重复步骤2和步骤3,直到找不到新的增广路径为止。此时若所有消费节点需求都被满足,则方案合法,否则非法。
2.3.2 SPFA算法实现
求解过程中的寻路算法采用SPFA算法,该算法可分为初始化和松弛两步操作,其实现步骤为:
步骤1 初始化。建立源点S到图中各点的距离数组distSPFA[N+1],S到本身距离为0,到其它所有点距离初始化为正无穷。然后建立访问数组visited[N+1],表示一个节点是否正在队列中,每个元素都初始化为false。路径记录数组parentSPFA[N+1]用于记录每个节点在路径中的前驱节点,所有元素初始化为-1。建立一个队列queue,初始时队列里只有源点S。进队次数记录数组enterQueueCount[N+1]用于记录每个点的进队次数,所有元素初始化为0。
步骤2 松弛操作。queue非空时,队首元素i出队,对以i为尾节点的所有边ei,j的头结点进行松弛操作:若distSPFA[i]+ei,j比distSPFA[j]小,则将前者赋值给后者,若j不在队中,则j入队,其入队次数enterQueueCount[j]加1,记录路径中j点的前驱为i,parentSPFA[j]=i,visited[i]设为1。若队列为空,结束算法。
2.4 实例分析
图4是一个实例的网络拓扑图。

图4 实例网络拓扑图
图4中圆圈为网络节点,三角形为消费节点,网络节点间链路上的标记(x,y)如章节1.3所述。每个消费节点只与一个网络节点直接相连,其对应的链路带宽租用费为0,链路上的数据表示该消费节点的带宽需求。本文算法需要从网络节点中选出部分节点部署服务器,以满足所有消费节点的带宽需求,同时使服务器部署成本及网络租用成本之和达到最小。
以上网络拓扑结构以文本文件形式记录下来作为程序的输入,文件格式如下:
网络节点数x1 网络链路数x2 消费节点数x3
单个视频内容服务器部署成本
链路起始节点ID链路终止节点ID总带宽 租用费
……(如上链路信息x2-1条)
消费节点ID相连网络节点ID视频带宽消耗需求
……(如上消费节点信息x3-1条)
以图4为例其输入文件形如:
28 45 12
100
0 16 8 2
……(如上链路信息44行)
26 27 19 1
……(如上消费节点信息11行)
由于输入文件篇幅过长,部分相似信息省略。文件输出格式如下:
网络路径数Line
(空行)
从服务器节点到消费节点的路径路径所占带宽
……(如上路径信息Line-1条)
cost:成本(千元)
算法耗时(毫秒)
图4实例的解决方案如图5所示。

图5 解决方案
解决方案给出19条路径,对应图5中的19行输出路径,每行第一个数据是服务器节点序号,后跟若干普通网络节点序号,倒数第二个数据是消费节点序号,最后一个数据是该条路径所占带宽。从图5中第3,4行可以看出,0号消费节点的带宽需求可由0号和22号服务器节点满足,带宽路径为0->8->0(分配了36 Gbps)和22->21->8->0(分配了4 Gbps),其它消费节点以此类推,如图6所示,0,3,22号网络节点为服务器节点,它们满足了所有消费节点的带宽需求,删去不必要的链路,剩下每条链路都标明了带宽大小和方向。该方案成本为783(千元),算法耗时26 ms。
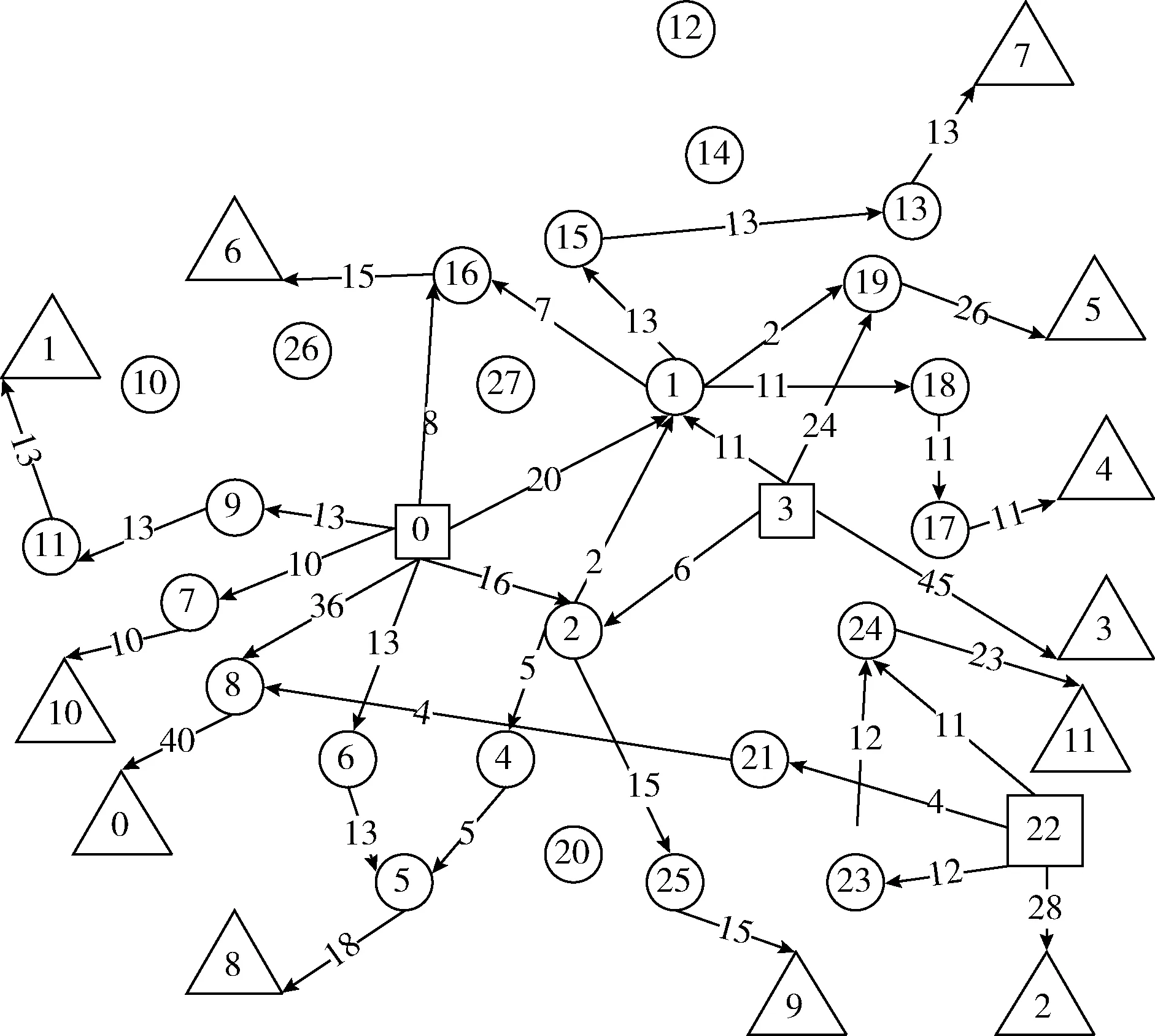
图6 解决方案
3 实验与结果分析
3.1 实验环境
本文使用的编程语言是C++,仿真环境如下:
CPU:intel(R) Core(TM) i3 CPU 550 @ 3.20 GHz 3.19 GHz
内存:2.00 GB
内核:单核
编译器:gcc 4.8.4
操作系统:linux Ubuntu 14.04.4 LTS 64位,内核版本Linux version 4.2.0-27-gineric
为了保证客观性和普适性,本文的实验数据来自第三届华为软件精英挑战赛提供的案例。
3.2 实验步骤
(1)输入:算法需要的输入数据从文件中读取,文件格式请参见2.4节,本次实验采用了4组不同规模的用例,分别是初级用例:50个网络节点,97条网络链路,9个消费节点;
低级用例:160个网络节点,606条网络链路,72个消费节点;
中级用例:300个网络节点,1134条网络链路,135个消费节点;
高级用例:800个网络节点,2939条网络链路,360个消费节点。
(2)输出:实验结果输出到文本文件中,文件格式请参见2.4节。
(3)结果分析:对上述多个案例的实验结果进行统计,并将计算结果与文献[9]提出的混合整数规划模型的计算结果进行性能比较。
3.3 仿真结果对比与分析
在不同规模下计算出的部署方案总成本(千元)和消耗的时间(ms)见表1和表2。

表1 两种模型在不同规模用例下的成本

表2 两种模型在不同规模用例下的耗时
由表1可以看出,初级,低级,中级,高级用例中MCMF模型分别比MIP模型减少了0%,1.1%,2.7%,4.3%的成本。可见对于小规模用例,前者与后者求取的最优解相差不大,随着规模的增加,MCMF的优势越趋明显,这个由图7更能直观地表现出来。
由表2可以看出,MCMF模型耗时比MIP模型多,这是因为前者求解最优解使用了模拟退火遗传算法,为了避免过早陷入局部极值,后期继续搜寻全局最优解而耗时增加,而后者在算法后期最优解成本已没有下降的空间。

图7 两种模型在不同规模下代价比较
图8为两种模型在相同规模案例的运算过程中成本随着时间变化的曲线。可以看出两者在算法前期寻找更优解的效率很高,随着当前最优解越来越接近全局最优解,效率逐渐降低。图中t时刻MCMF模型的代价有个小幅的下降,这是因为算法在寻优过程中跳出了某个局部极值,成功避免了早熟现象,而MIP模型无法寻找到更优解,过早地结束了算法,这与表1和表2的记录相吻合。

图8 代价-时间变化
4 结束语
本文基于流媒体服务器部署问题中服务器数量和位置不确定性,以及网络结构中每条链路都有带宽和租用费双重限制的特性,将多源点多汇点的网络结构改造成单源单汇的结构,建立了MCMF模型。设计了模拟退火遗传算法求解该问题,并与前人提出的基于MIP模型的贪婪分解算法进行比较。实验结果表明,该模型在求解最优解方面胜过MIP模型,用例规模越大,前者的该项优势越明显,作为代价,算法耗时有所增加,因此在算法效率方面有待进一步研究。

