地铁隧道结构变形监测中的奇异谱分析

王 涛 田林亚 王文峰 毕继鑫 黄岩松

(1. 河海大学地球科学与工程学院， 211100， 南京； 2. 绍兴市上虞区规划分局,312300,绍兴//第一作者，硕士研究生)

为保证地铁结构的安全，应对其进行全方位的安全监测[1-3]，掌握既有地铁工程结构在新建项目施工过程中所发生的变化，为建设单位及地铁单位提供及时、可靠的信息。其中，自动化、智能化监测是今后地铁安全监测的主要发展方向[4]。如何实时准确处理大量监测数据，获取地铁结构变形趋势和变形周期，是一个值得研究的问题。相关学者采用了自适应卡尔曼滤波、时间序列、小波时间序列等方法进行沉降数据处理[5-7]，但其在预测变形周期等方面存在一定的不足。地铁监测环境具有一定的特殊性，监测人员只能在列车停运以后进入隧道进行监测，一般只有3～4 h可以利用[8]，且需提前一个月将监测计划报备地铁管理部门。因此，需制定合理的监测计划，保证监测工作既能监测到隧道的变化，又不会造成人力和资源的浪费。奇异谱分析是当前处理时间序列十分有效的数学分析方法[9-10]，能够根据不同应用目的将信号分解为趋势项、周期项、噪声项等不同成分，可以有效去除观测数据中的噪声，获取变形趋势和变形周期。本文将奇异谱分析方法应用于地铁沉降监测数据处理，并将处理时间序列数据十分优异的小波分析方法应用其中作为对比，以证明本方法的有效性。

1 奇异谱分析理论

奇异谱分析是近年来兴起的用于研究非线性时间序列十分有效的数据分析方法[11]。其核心思想为：将一维时间序列转换为多维空间序列进行主成分分析，分解为多个有效成分，并根据需要选择若干分量进行重构，提取出信号的变化趋势、周期和噪声等不同成分。

首先，将一维时间序列xi=x1,x2,x3，…，xN转化为时滞矩阵X：

(1)

式中：

M——嵌入维数，代表窗口大小。

其次，对X进行时间经验正交函数展开(TEOFs)，得到滞后协方差阵D：

(2)

然后，求解D的特征向量Ek和特征值λ1≥λ2≥…≥λM，这些特征值被称为时间序列xi的奇异谱，对奇异谱进行重建的运算称为奇异谱分析。λk对应的特征向量Ek为时间经验正交函数(TEOF)，定义第k个时间主分量(TPC)为序列xi在Ek上的正交投影系数，aik代表权重，则：

(3)

奇异谱分析中最重要的步骤是重建[12]。重建的过程，就是由TEOF和TPC重建一个与原始序列等长的序列，其公式为：

(4)

所有重建成分之和等于原始序列[13]。

随着自动化监测工作的实施，必须采用新的方法处理大量的监测数据，将已有数学模型应用于监测数据的处理是十分有益的一个方向。本文以沉降监测为例，研究奇异谱分析在地铁监测数据处理中的应用。

2 工程概况

2.1 工程背景

由于地铁附近新建项目，必须实时监测地铁隧道受到基坑开挖及项目建设过程的影响，以保障地铁运营安全。地铁监测具有如下特点：① 监测时间短，受到地铁运营时间的限制，隧道监测只能在地铁停运以后进行，一般情况下只有3～4 h可以利用；② 隧道环境特殊，相对于一般的监测项目，隧道监测在狭长、黑暗的环境下进行，对监测手段和方法有更高的要求；③ 精度要求高，地铁隧道埋深大，周边建筑物多，结构内应力大，整体变形量小，所以对监测精度有更高的要求；④ 提前制定监测计划，为保障地铁每日正常、安全运行，监测工作的实施受到地铁部门的管理，一般需要提前一个月制定监测计划，包括监测的日期和拟监测的内容等。新建建筑为酒店式公寓楼，设置二层联体地下室。其中，基坑面积约18 540 m2，周长约560 m，开挖深度约为9.2 m。基坑位于地铁隧道北侧，对应地铁里程大概为K21+017～K21+145，长度约为128 m，基坑围护结构边线距地铁隧道结构边线最近约为25.4 m。基坑垫层底比隧道顶部高1.88～4.84 m。图1为基坑与地铁的平面位置关系及沉降监测点的分布。

2.2 监测方法

如图1所示，在地铁两端布设4个沉降监测基准点(JZ1～JZ4，JY1～JY4)。沉降监测基准点布设在远离地铁变形区120 m的轨道底板上；在基坑边线正对的隧道区间内，左线约每10 m布设一个监测点，右线约每20 m布设一个监测点。监测采用Trimble DINI03电子水准仪，在夜间配合铟瓦条码尺和照明灯具，采用科傻平差软件根据相关规范以测站数为权进行严密平差。基准网初期进行2次独立观测，误差范围内取均值确定各基准点的初始高程。每月定期对基准网进行复测，并将检测高程值与原采用值进行比较，若检测的高程值与原值的较差大于2倍高程中误差时采用新值，否则采用原值。平时采用附和水准路线，从基准点JZ2(JY2)测至JZ3(JY3)，获得各期点位沉降值和累计沉降值。

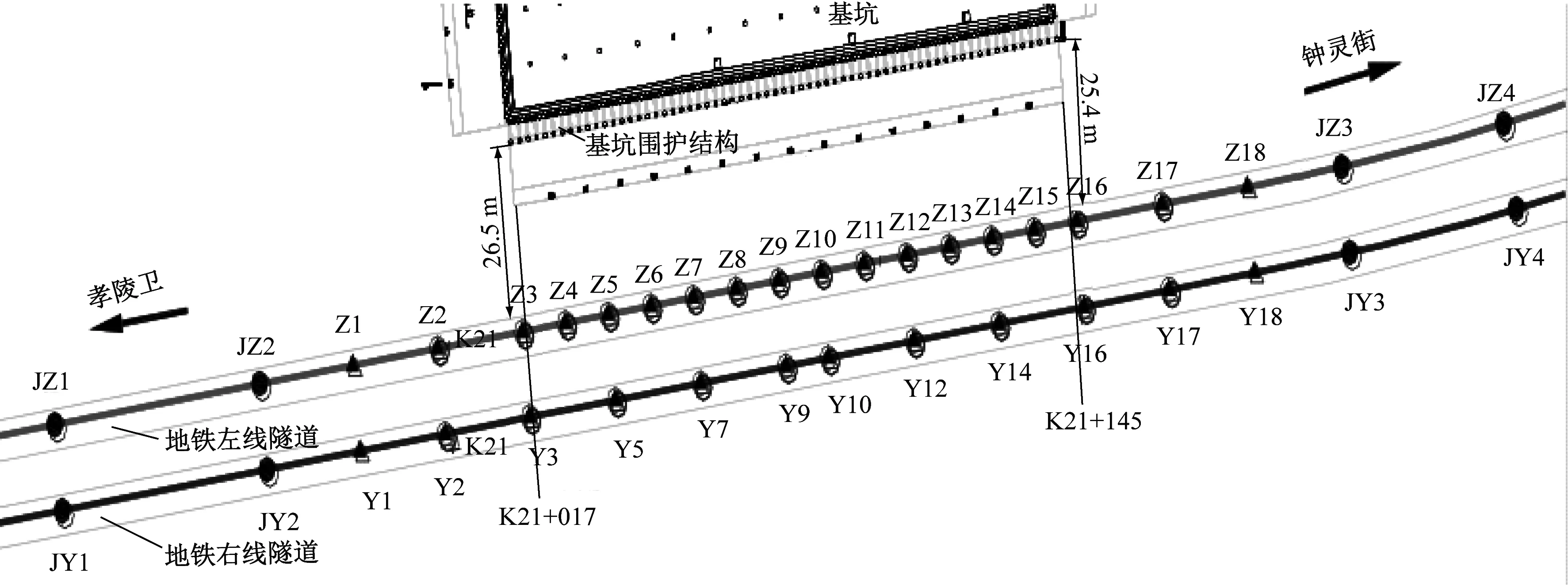
图1 基坑与地铁平面位置及沉降点布置示意图

3 试验分析

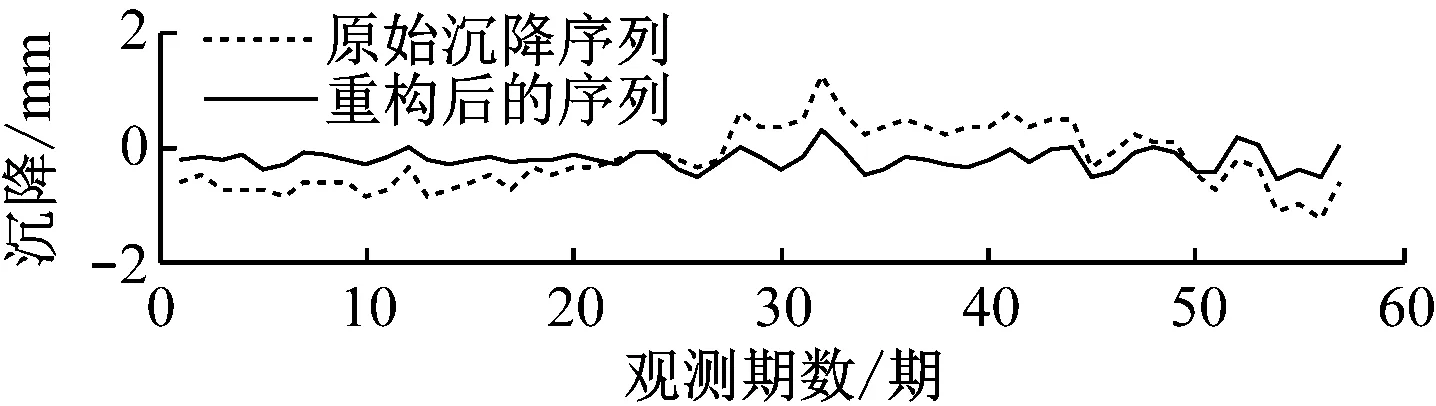
自监测工作开始，共监测了57期。本文选择左线有代表性的Z4、Z10、Z15三个监测点。三个监测点的原始沉降序列如图2所示。可以看出，自监测实施以来，三个监测点的沉降变化趋于一致，但无法获取观测点的变化趋势和变形周期，给衡量地铁安全状态带来困难。本文利用具有优异时频特性的小波分析对原始数据进行处理，获得观测数据的变化趋势作为参考；然后利用奇异谱分析处理(利用了MATLAB软件编程实现)监测数据，将获得的结果与小波分析结果对比分析。

a) Z4原始沉降序列

首先采用小波分析方法处理数据，选择去噪效果好的sym3小波基进行3层小波分解，并采用全局阈值的方法进行小波阈值降噪[14]，然后进行小波重构，得到去噪后的沉降序列(见图3)。由图3可见，经小波去噪后沉降序列变得光滑，且变化趋势明显。整体上看，Z4、Z10、Z15三个监测点的变化趋势基本相同，可以认为基坑开挖对地铁线路最大影响区段Z3～Z16的沉降影响基本一致。此外，Z15沉降序列的第55期观测值表现异常，经对比原始数据，发现该点前后两次观测值较差较大，判断其为粗差，应给予剔除。小波分析能有效获得沉降变形趋势，但不能获得地铁的沉降周期，本文利用奇异谱分析方法对此进行研究。

奇异谱分析中一个重要的因素就是窗口大小的选择。根据选择窗口的大小不大于原始沉降序列1/3的原则，选择窗口M=18进行奇异谱分析，获得原始沉降序列的趋势项和周期项。图4和图5分别表示了奇异谱分析后原始沉降序列的趋势和周期。从图4中可以看出，奇异谱分析较好地拟合了沉降序列的变化趋势，呈现出了地铁沉降的变化特性。对比图3、图4可知，小波分析和奇异谱分析在变化趋势的表现基本一致，奇异谱分析结果更光滑，拟合效果更好。但是，奇异谱分析过滤掉了可能存在的异常值信息，细节表现不如小波分析好，不利于异常值的判断。

a) Z4原始沉降序列小波去噪

a) Z4奇异谱分析趋势图

观察图4可知，沉降序列在前20期表现为在0值下方小位移量沉降，之后慢慢反弹至0值上方，可以认为在观测初期基坑尚未开挖，工程设备进场地面负重增加，使得地铁出现沉降，随着基坑的开挖，地面负重减少，沉降点慢慢反弹。沉降序列在20至50期表现为上升的趋势，监测到该时期基坑进行了大量的开挖，并且地铁内部出现渗漏的情况，说明这个时期基坑开挖使得隧道底部出现反弹，基坑开挖对地铁的影响明显。图6为地铁隧道中几处明显渗漏处，显示了受基坑影响的地铁现状。监测时需要特别注意此阶段的沉降量，并加强监测的频率。沉降序列在51期以后表现为逐渐下降到0值以下的趋势，说明地铁线路在受到基坑影响上升后又随着建筑物基础的建设逐步下沉。以上表现均符合相关工程的一般变化规律。

a) Z4奇异谱分析周期图

图5为奇异谱分析提取出的周期项，这是小波分析不具有的数据处理特性。从图5中可以发现，3个观测点振动的幅度和周期整体变化情况一致，都表现为前期振幅偏小，后期振幅变大。说明前期地铁受基坑开挖影响较小，在30期以前监测点振幅较为稳定，因为此阶段基坑稳定持续的开挖，地铁受到的影响较为稳定。随着基坑开挖深度的增加，地铁受到的影响增加，在30期以后监测点振幅变大，此时基坑开挖深度接近地铁埋深。在51期受基坑回填的影响，监测点振幅偏大。图5中显示的变形情况与真实情况基本一致。在地铁监测时可据此了解监测周期和频率，制定合理的监测计划。以图5中Z4监测点为例，可以将变形周期分为3段：第一段为前20期，由于振幅较小且周期稳定，监测时较少的监测次数就能获得点位变化，可以据此减小监测频率，以减少监测成本；第二段为21～50期，此时振幅和周期偏大，监测频率相应增加；第三段为51～57期，沉降值明显变大，说明当下的监测频率已不能完全表现地铁变形，需要增加监测频率，获得更详细的变化情况。

4 结语

为了保证地铁隧道结构的安全，对地铁隧道进行常规的结构监测和定点的保护区监测十分必要。在对地铁的沉降、水平位移、隧道收敛和隧道断面等进行监测时，数据量大，可利用的时间短，一般当天的监测数据第二天就要给出监测报告，所以利用新的方法准确处理监测数据，获取变形趋势和异常值，预测变化趋势和周期，对地铁监测工作的实施和安排十分有益。本文将当前处理时间序列十分有效的奇异谱分析理论应用于地铁安全监测中，并以某地铁的沉降监测数据为例进行分析，获得了较好的处理结果，发现了奇异谱分析在获得变形周期方面的能力，可为监测人员评估变形情况和制定监测计划提供参考。存在的问题是，在奇异谱分析时对其中的周期变化机理研究不多。下一阶段将对其进行研究。

里程：YK21+067