基于谐波分量系数控制的低电压穿越策略研究
祝兴星,郑伟华,刘境雨
(湖南工业大学电气与信息工程学院,湖南 株洲 412007)
0 引言
现如今随着化石能源消耗的快速增长,全球各地频繁出现异常突出的气候、环境问题,全世界对清洁无污染的可再生能源都无比青睐。风能便是其中之一,它作为一种清洁无污染的能源,具有可再生、储量大、无污染、能量大、前景广等优点。随着世界各国把风力发电作为战略选择,风力发电产业和技术都得到了跳跃式发展。因此,不管是在规模化开发、商业前景层面,还是在成熟的技术层面,风力发电都逐渐成为了时代的宠儿[1-4]。
DFIG的控制系统受电网电压方均根值的快速变动而影响较大,当电网电压降落时不能保证设备正常所需的电功率也无法维护电感电容的磁场平衡,这样会使得电网电压的情况每况愈下。如果这一现象无法得到有效的控制将有可能使得整个风电场的脱网,甚至造成局部电网的瘫痪。所以解决低电压穿越问题已经成为风力发电人的一个共同目标。
针对电压跌落时DFIG的电磁响应,目前的研究成果都是建立在交流电机动态行为分析基础之上。当定子的并网电压下降时,在电动机内部激励强电磁瞬态过激励过程。这导致定子和转子上的瞬态过电压和过电流。文献[5]分析了DFIG故障过程中转子侧变流器对控制系统的影响。给出了短路电流的解析表达式,但这种表达式更复杂,难以应用于实际工程中。文献[6]提出了一个解决电压跌落故障的方法,引入其它的电压分量(转子上的电压分量)控制,通过对时间常数的推导,表明此控制方法可以加快暂态的过渡过程。本文从控制策略的角度出发,针对 DFIG在电网电压跌落时的暂态电磁特性,提出了一种令谐波分量系数为零的控制策略,用于消除过渡期间谐波电流的影响。采用这种控制策略,使得在过渡过程中的并网侧定子电流中只存在直流分量和基波分量,削弱了电流、有功和无功的剧烈波动;对电压跌落深度与电流、有功和无功进行的解析表明,DFIG在该控制策略下能够保持不脱网运行的同时也向电网注入了无功功率,有助于电网电压的恢复。仿真结果证明了理论分析的正确性,同时表明,该控制策略消除了电压跌落过渡过程中的定、转子侧谐波电流,实现了保护并网转换器的目的,可以有效提高双馈风力发电机的低电压穿越能力。
1 DFIG及其在电网电压跌落下的特性分析
1.1 DFIG的数学模型
DFIG的系统结构图如图1所示。采用绕线式异步电动机,定子绕组直接挂网,并流过工频的三相对称交流电。产生角速度的旋转磁场,转子绕组通过双PWM转换器连接到电网,并流过频率可调的三相交流电。产生相对于转子[7]以滑动角速度旋转的磁场。DFIG输出到电网的总功率包括定子侧输出功率和通过逆变器的转子侧输出之和。

图 1 DFIG的系统结构图Fig.1 DFIG system structure diagram
假设定、转子三相绕组对称且不考虑零轴分量,在三相对称条件下,建立两相同步旋转的dq坐标系,采用电动机惯例,则两相同步速旋转的dq坐标系中DFIG数学模型可表示为:
磁链方程:

式中,Ψsd、Ψsq、Ψrd、Ψrq分别为定、转子磁链的d、q轴分量;isd、isq、ird、irq分别为定、转子电流的d、q轴分量;Lm为dq坐标系中的等效绕组间的互感;Ls为dq坐标系中两项绕组自感(定子上的等效自感),Ls=Lm+Lls;Lr为dq坐标系中两项绕组自感(转子上的等效自感);其中,
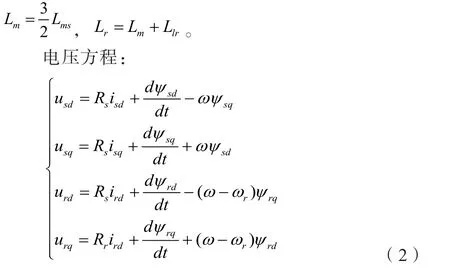
显而易见usd、usq、urd、urq分别为两轴上的电压分量。
DFIG的运行控制主要是功率控制,在电网出现故障时实施的就是对有功功率的有效控制,而无功功率的控制在确保电网电压稳定和满足系统无功功率需求时也是十分重要的控制目标[8],因而必须对DFIG的有功、无功功率关系作出分析。以标幺值表示的DFIG的瞬时有功功率和无功功率的表达式如下。
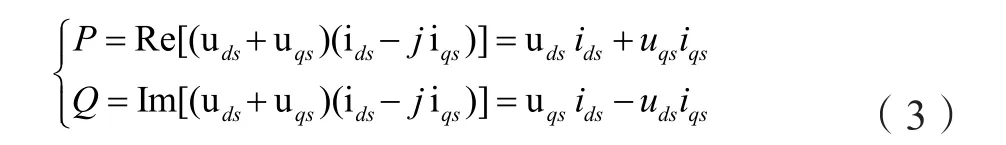
1.2 DFIG在电压跌落下的过渡过程
当电压下降时,消除谐波分量的控制策略必须考虑电网电压下降时发电机的电磁转换过程。在过度过程的影响上还需考察转励磁电压。如果在电网电压下降的同时改变转子激励电压,则可以根据叠加原理执行转子励磁控制下的电网电压降的转变过程。它被认为是在下降之前的稳定操作状态和具有一定下降深度的反向电压的过渡过程的叠加。
(1)与电压跌落前一样的稳态运行过程。稳态运行时,在同步速旋转的dq坐标系中的电流分量和电压分量均为常量。根据公式(1)和(2)得到以电流为变量所描述的DFIG电磁暂态过程的状态空间方程为:

其中A和B是状态空间方程的系数矩阵,当前电流列向量是:I=[idsiqsidriqr]T,电压列向量为:U=[0 1 udruqr]T。
(2)k倍反向电压的转换过程。如果电压降时的转子激励电压与下降之前相同,则当加上k倍反向电压时,DFIG的状态空间方为:

式中,电压列向量为:U=[0 k udruqr]T。
对式(4)和(5)可以得到,把对电压跌落下的数学模型的分析转换成了与电压跌落前一样的稳态运行时数学模型的分析和加反向电压时过渡过程数学模型的分析的叠加。
2 消除谐波电流的控制策略
2.1 定子电流推导
基本思路为:对公式(5)进行拉氏变换形成矩阵形式的代数方程,在此代数方程中求得定子电流和转子电流的解。然后通过拉氏逆变换从而求得在dq坐标系中的电流。最后再通过dq0到ABC的坐标变换即可求得在电压跌落时定、转子电流。为此对式(5)进行拉氏变换并进一步带入并化简得:
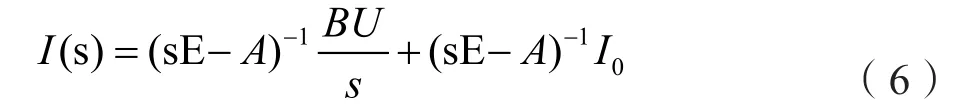
其中:E为单位阵,I(s)复域里的电流列向量;I0复域电流列向量的开始值。
等式(6)中复域中电流的dq分量是状态变量,状态方程通过拉普拉斯变换转换为复域中矩阵形式的代数方程。并与式(4)的解进行叠加,即可以得到在加反向电压的同时改变转子励磁电压的过渡过程在复域内的数学模型如下式所示。

其中Afk(s),Cfk(s)为与电机参数和电压跌落深度有关的矩阵。
上述模型是矩阵形式的代数方程,其中由定子电流的dq轴分量和转子电流的dq轴分量形成的当前列向量是未知变量,可以利用矩阵的运算直接对其进行求解。所求结果再经坐标变换后即可得到在加反向电压时定、转子的电流表达式,此结果再与跌落前稳定运行的初始电流相叠加,即可求得电压跌落时同时改变转子侧励磁电压下定、转子电流的解析表达式。
电压跌落下的定子电流为:
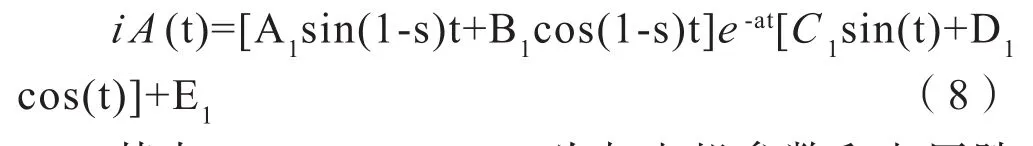
其中A1,B1,C1,D1为与电机参数和电压跌落深度有关的矩阵。
2.2 转子励磁电压控制策略
本文拟采取对谐波分量系数进行控制的方法,通过控制转子侧励磁电压,令谐波分量的系数为零,从而消除谐波电流对暂态过程的影响。其中转子侧d轴分量为额定值的kd倍;q轴分量为额定值的kq倍[1]。
令谐波分量的系数为零,则可以得到:

通过对上式的求解,则可以得到:

所以,在电网电压发生跌落时,为了消除谐波电流的的影响,DFIG在转子侧需要施加的励磁控制电压为:

其中udrc和uqrc分别为此控制策略下的转子侧励磁电压的给定值。
2.3 计及控制策略影响的电流瞬态特性
在电网发生电压跌落故障时,通过给定满足式(11)的转子励磁电压给定,可得在该控制策略下的DFIG定子电流为:

式(12)表明,在计及控制策略时的转子励磁电压控制下,定子电流中不存在谐波分量,只有恒定的基波分量和直流分量,并且其幅值取决于发电机的具体参数、发电机的运行状态及电压跌落深度。因此对并网端来说,无谐波分量影响即低电压穿越时对电网无谐波污染,不会影响电网的电能质量。
2.4 计及控制策略影响的功率瞬态特性
在同步旋转dq坐标系中,根据P=iqs(t)、Q=ids(t),现对电压跌落前注入电网的瞬时有功功率和无功功率的分析分别如下所示:
在本文所采取的控制策略下,由于消除了暂态过渡过程中谐波电流的影响,使得DFIG向电网注入的有功功率和无功功率中包含了两种分量:基波分量和直流分量。由于基波分量在一个周期内的平均值为零,所以低电压故障的运行方式下,双馈电机注入电网的平均有功和无功功率经推导如下所示:

从式(13)~(14)中可以看出,两种运行方式下存在如下的关系:
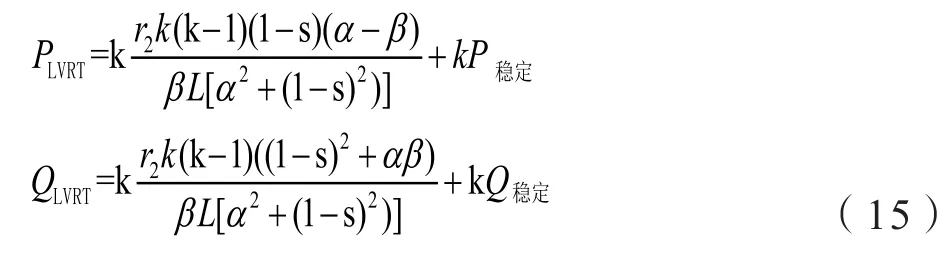
在本文的分析中,DFIG采用的是电动机惯例,因此在稳态运行时的P稳<0和Q稳<0。由于L1Lm和L2Lm,故有α β。而且电压跌落深度0<k<1,所以由式(15)可知即在 QLVRT<0,即在本文采取的低电压穿越控制策略下,DFIG在保持不脱网运行的同时也向电网注入了无功功率,这将有助于电网在低电压故障下的恢复。
3 仿真分析
为了验证该低电压穿越控制策略的有效性和理论分析的正确性,对其进行了基于MATLAB/Simulink平台的仿真,选用一台1.5 MW的双馈感应电机,具体仿真参数如下:额定电压690 V,L1=0.18,L2=0.16,Lm=2.9,r1=0.03,r2=0.016。 本文选取电压跌落深度系数k为0.3,即从电网的额定电压跌落到额定值的30%。
设稳定运行时,电机定子电流为额定电流,转差率s=0.05,转子侧的励磁电压为udr=0.0185,uqr=0.0474。在上述稳定运行的条件下,电网发生电压跌落故障,此时保持电网电压跌落前后的转子侧的励磁电压不变,即不采用本文所提控制策略。可得在电压跌落下的到定子A相电流,如图2所示。
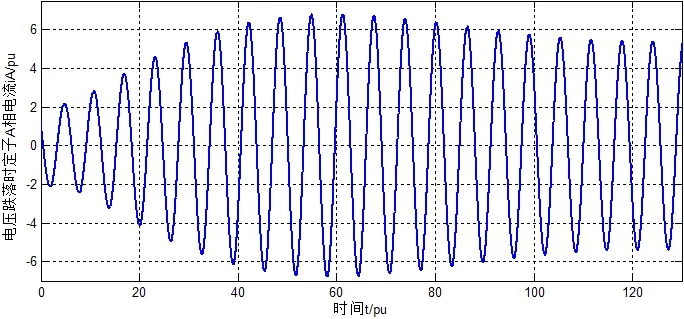
图 2电压降落时定子A相电流Fig.2 A phase current of the stator voltage drop
从图2可以看出,在电网发生电压跌落故障时,定子绕组中产生较大的冲击电流,而且冲击电流的持续时间比较长。若对此不采取必要的抑制措施,继续保持发电机的并网运行不仅会对电网产生很大的冲击,而且还会有大量的谐波电流注入电网,将严重影响电网的电能质量和运行安全。所以必须在电网发生电压跌落故障时对DFIG进行可靠有效的控制。
本文所提出的低电压穿越控制策略是通过给定满足式(11)的转子侧励磁电压以消除过渡过程中的谐波电流影响。设在电网发生电压跌落故障时,采用所提控制策略,其转子和定子的相电流仿真结果分别如图3、图4所示:

图 3 改用控制方法前后转子a相电流Fig.3 Before and after the control strategy of rotor phase current a
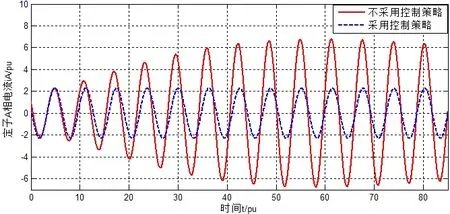
图 4 改用控制方法前后定子A相电流Fig.4 Before and after the control strategy of stator phase current A
从图3可以看出,若不采用消除谐波分量的控制策略,转子电流的冲击幅值将达到6~7 pu,约经过16个周波才稳定下来,稳定后电流的幅值仍可达5 pu之多;而在采用该控制策略后,转子电流的幅值大大下降仅为2 pu,约10 ms即趋于稳定,大大缩短了过渡过程,满足了并网技术规范的要求,因此DFIG能够保持不脱网运行。从图4的定子A相电流可以看出,在该控制策略下,低电压故障的过渡过程只包含恒定的基波电流分量,使得保持并网运行的同时不会向电网注入谐波电流。另外,对比图3和图4可以看出,转子电流的幅值和定子电流的幅值基本大小相等,相位相差180°左右,这是由于DFIG在结构上类似于绕线式异步电机,其励磁绕组的阻抗值很大,可以忽略不计的原因[9]。
取有差别的电压下降程度k,对在转子侧励磁电压把控下的有功和无功搭建仿真分析,可用功率和电压降深度系数之间的关系如图5所示。

图 5 功率与电压跌落深度的关系Fig.5 Power relationship with the depth of the voltage drop
从图5中可以看出,当电压降落系数为0.5左右时,在该控制策略DFIG对电网馈送的无功功率将达到最大值,而有功功率则一直呈线性,这也有利于对有功功率的控制。由于文中数学模型的建立是以电动机惯例的,因此当电机向电网输出有功功率和无功功率时,其幅值始终是负值,
4 结论
本文分析了在电网电压跌落时DFIG的电磁暂态特性,并由此得出了电压跌落产生的机理以及电流、功率特性。通过对定子全电流表达式的定性分析,提出了一种令谐波分量系数为零,从而消除暂态过程中的谐波分量影响的控制策略,理论分析及仿真结果表明:该控制策略在电压跌落的暂态过度过程中,消除了定、转子侧的谐波电流分量,平缓了暂态电流和功率的剧烈波动,实现了对网侧变换器的保护;DFIG在保持不脱网运行的同时也向电网注入了无功功率,这提高了DFIG的低电压穿越能力,将有助于电网电压的恢复。双馈风电机组对无功功率的支持能力将在以后的研究中继续进行,并拟在一台WT 1500-D88的风电机组上进行无功功率支持能力和低电压穿越的实验验证。

