药协调臂刚柔耦合动力学仿真
,,
(南京理工大学机械工程学院,江苏 南京 210094)
0 引言
在对药协调臂进行现场实验时发现,在运动过程中药筒有非常明显的振颤,这与多刚体模型进行动力学分析得到的结果对比差异很大。
工程上对臂架系统进行研究时,往往只是把臂架系统作为刚性体进行分析,忽略了臂架的弹性变形以及柔性体变形对整个系统的影响;但是,在较大的加速度及大载荷的情况下,臂杆会发生一定的变形,而关键零件的微小变形以及弹性振动都可能会对系统产生巨大的影响;因此,不能忽略臂架的柔性变形及弹性振动对整个系统的影响[1]。
因此本文准备将药协调臂模型中的双连杆、上连接板、上支杆做成柔性体模型,将相应的刚性杆件换成柔性杆件,然后组成刚柔耦合模型;将仿真的结果与刚性模型仿真得到的结果进行对比,从而为后来的进一步优化提供了理论依据。
1 药协调臂的结构与工作原理
当火炮准备射击时,药协调臂在协调油缸的驱动下绕耳轴转动至固定取药位置从药仓接取药块,之后在协调油缸的驱动下使药协调臂的大臂转动至与身管轴线平行的位置,然后在翻转油缸的驱动下,药协调臂上的四连杆机构翻转伸出,使药筒的轴线与身管的轴线重合,然后电机转动,驱动协调臂上的链条将药块输送至炮膛。本文研究药协调臂在翻转油缸的驱动下使药筒的轴线与身管的轴线平行这一过程。对药协调臂的三维模型用三维模型软件Creo2.0画出并组装成总装配图,如图1所示。

图1 药协调臂的初状态
2 药协调臂多刚体动力学仿真分析
2.1 刚性模型的动力学仿真
将药协调臂零件的三维模型在Creo2.0里装配完成后,将模型保存为*.x_t格式文件并导入Adams中生成多刚体模型。这里要求Creo2.0中模型的单位与Adams中的单位保持一致。
在Adams中给模型添加运动副和载荷;为翻转油缸设置驱动函数,设定的仿真时间为0.9 s,驱动油缸的规律运动:0~0.2s速度由0加速到124 mm/s,0.2~0.7 s速度保持不变,0.7~0.9 s速度由124 mm/s减速到0;得到刚性模型运动过程中药筒质心的速度和质心的角速度,如图2、图3所示。

图2 刚性模型药筒质心的速度

图3 刚性模型药筒质心的角速度
2.2 仿真的结果分析
从图2可以发现,药筒质心点在X和Z方向的速度变化平稳,并没有明显的突变,在Y方向的速度为0;从图3可以发现,质心点角速度是一条光滑的曲线,并没有明显的突变。所以对多刚体模型进行分析的时候,得到的结果是符合理想状态。
3 药协调臂刚柔耦合动力学仿真分析
3.1 刚柔耦合系统动力学的建模原理
现在学者们对刚柔耦合系统建立模型时,运用的方法可能不同,但是基本原理都是一样的,包括刚体运动和变形的运动学描述以及使用哪一种力学原理来建立模型等方面。
大范围的刚体运动的准确运动学描述以及相对小的变形是研究刚柔耦合首要解决的问题,运动学的描述取决于选择哪一种坐标系,常用的有浮动标架法、共旋标架法和惯性标架法,3种方法有个共同点,那就是要求刚柔耦合模型在没有变形的情况下依然能转化为刚体动力学以及在没有刚体运动的情况下能够退化为变形体力学[2]。
对刚柔耦合模型建立动力学模型有很多种方法,最常用的有第二类拉格朗日方程、哈密尔顿原理、牛顿-欧拉方程等;对于臂架系统主要采用的是第二类拉格朗日方程,因为这个方法可以方便借助计算机进行计算。将臂架系统的动能Ek及势能Ep相差定义为拉格朗日函数为:
L=Ek-Ep
(1)
因此,系统的拉格朗日方程可表示为:
(2)

3.2 刚柔耦合模型的建立
用Adams建立刚柔耦合模型一般都是先使用功能强大的有限元分析软件如ANSYS、ABAQUS等来建立复杂零件的柔性体,生成格式为.mnf的模态中性文件,然后在原有刚体模型的基础上,将相应的刚性体用已生成的柔性体替换,再重新施加载荷和约束便得到了刚柔耦合模型。
将文中已在Creo2.0中建立好的零件模型导入ANSYS中,设置模型的密度、弹性模量、泊松比等参数,对零件进行网格划分。在零件需要与其他零件相连接的部位建立刚性区域,刚性区域定义了各铰接点与相关节点之间的力与位移关系,以实现在Adams刚柔耦合仿真中运动与力的传递[4]。
(3)
Fij=ljFi,i=x,y,z,j=1,2,,n
(4)
Ui表示刚性节点的总位移;Uij表示j节点在i方向的位移;kj表示j节点对Ui的影响因数,该因数与刚性节点周围节点的位置相关;Fi为刚性区域在i方向上的受力;lj为j节点对刚性节点受力的影响因数,该因数与刚性节点与周围节点的位置相关;i表示三维坐标系的3个坐标方向;j表示刚性节点相连接的节点数[5]。其中,构件的模态决定了kj与li,各个节点的实际位移和实际受力是模态的按照一定比例的叠加,通过系数kj与系数li描述这种比例关系,如果系数kj与系数li越大,则模态对构件总位移或受力的贡献量就越多[6]。这样通过ANSYS计算就可以得到Adams所需要的格式为.mnf的模态中性文件,如图4~图6所示。这里需要保证在ANSYS中生成的模态中性文件的单位与Adams中单位相统一。将生成的模态中性文件导入Adams中替换相应的刚性零件,就得到刚柔耦合模型。

图4 上连接板柔性体及刚性区域模型
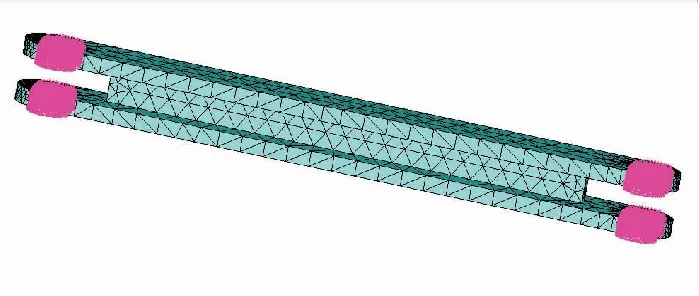
图5 上支杆柔性体及刚性区域模型

图6 双连杆柔性体及刚性区域模型
3.3 刚柔耦合模型的仿真
对刚柔耦合模型施加与多刚体模型同样的驱动,得出的结果,如图7和图8所示。
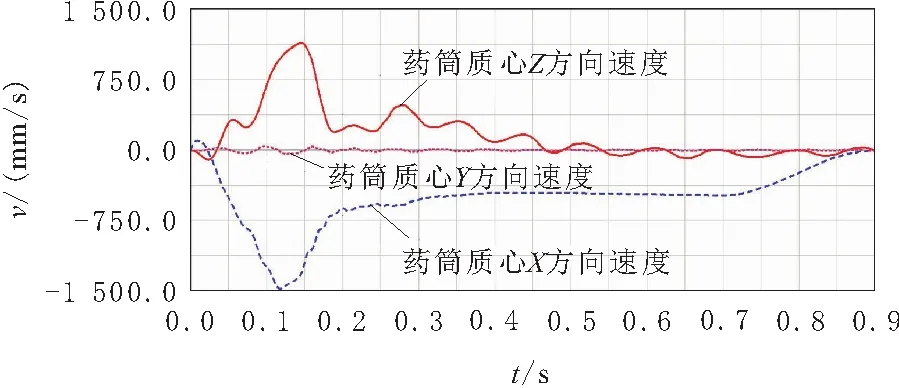
图7 刚柔耦合模型药筒质心的速度

图8 刚柔耦合模型药筒质心的角速度
3.4 多刚体与刚柔耦合模型仿真结果对比分析
将图2和图7对比,在同样的驱动下,多刚体模型和刚柔耦合模型的药筒质心的速度的整体变化规律相同,但是在刚柔耦合模型下的Z方向(竖直方向)的速度波动明显比较大,这也解释了药协调臂在实际试验过程中的振颤现象。图3和图8分别表示刚性模型下药筒和刚柔耦合模型下药筒的角速度,由对比看出,刚性模型下药筒角速度变化非常平稳,刚柔耦合模型下的药筒角速度变化频率非常高,波动幅度非常大,有非常明显的突变。
仿真结果表明,臂杆实际运动过程中弹性变形和弹性振动对整个系统的影响是非常大的,因此在对臂架系统进行分析的时候最好把关键部位的零件作为柔性体来考虑;同时结果也表明刚柔耦合模型与工程实际更加接近。
4 结束语
通过联合三维建模软件Creo2.0、有限元分析软件ANSYS以及多体动力学分析软件Adams对某药协调臂进行了刚柔耦合动力学仿真分析,得到了药协调臂在刚柔耦合状态下的运动规律;对比发现,如果把机械系统简化为多刚体模型,则得到的仿真结果是理想化的与实际情况相差较大,而运用刚柔耦合模型更加接近实际工程情况。对药协调臂采用刚柔耦合分析,后续可以输出ANSYS所需要的载荷文件(.lod文件),载荷文件记录了运动过程中柔性体的运动状态和受到的载荷,将载荷文件导入到ANSYS中得到各个零件的动态应力分布及时变的节点力,为结构分析及优化提供了理论依据。

