基于CEEMD的滚动轴承振动信号自适应降噪方法
,
(西南交通大学机械工程学院,四川 成都610031)
0 引言
作为旋转机械设备中最易发生故障的部件之一,滚动轴承的故障诊断对设备的正常运行和生产安全具有重要意义。在实际工况下,由于受到工作环境和传输路径等因素的影响,滚动轴承振动信号中的故障特征信息往往被噪声所掩盖,难以准确提取出来[1]。因此,采取合适的方法对故障振动信号进行降噪处理对提取滚动轴承的故障特征至关重要。
CEEMD对非平稳、非线性的滚动轴承振动信号有很好的处理效果,但是没有提出判断信噪分量分界点的方法。同时,采用传统阈值函数的小波阈值降噪方法并不能很好地提取低阶固有模态函数分量中的高频有效信息。因此,本文在信号自相关函数特性的基础上,提出了利用固有模态函数分量归一化自相关函数曲线的单边波峰宽度与峰宽占比自适应确定CEEMD信噪分量分界点的方法,并对噪声分量进行改进小波阈值降噪以提取其中的高频有效信息。该方法较好地弥补了原有方法的不足,同时保留了滚动轴承振动信号中的突变细节,在抑制随机噪声的同时保证了重构信号的完整性。
1 CEEMD原理
互补集合经验模态分解(complete ensemble empirical mode decomposition,CEEMD)[2]是在经验模态分解(empirical mode decomposition,EMD)[3]和集合经验模态分解(ensemble empirical mode decomposition, EEMD)[4]的基础上改进的一种信号自适应分解方法,本质上还是属于EMD。CEEMD的具体实现过程如下[5]:
步骤一,向原始信号中加入N组正、负成对形式的辅助白噪声,由此得到的集合信号的个数为2N。辅助噪声是均值为0,幅值系数k为常数的高斯白噪声ni(t)(i=1,2,,N)。当N取100~300时,值选取0.01~0.5倍信号的标准差。
(1)
x(t)为原始信号;ni(t)为辅助白噪声;xi1(t),xi2(t)为添加噪声后的信号对。
步骤二,对得到的2N个信号进行EMD分解,每一个信号都可以得到一组IMF分量,记第i个信号的第j个IMF分量为IMFij,将残余分量作为最后一个IMF分量。
步骤三,将对应的IMF分量进行平均运算,就可以得到信号x(t)经CEEMD分解后的各阶IMF分量:
(2)
IMFj表示原始信号经CEEMD分解后得到的第j个IMF。
2 CEEMD自适应降噪方法
在应用CEEMD方法时,根据信号的自相关函数特性可以对分界点进行粗略判定,但因为它是基于经验知识的,存在一定的主观性,误差较大。在此基础上,本文进一步提出了利用自相关函数的单边波峰宽度自动确定CEEMD信噪分量的分界点,并结合改进小波阈值降噪方法,提出了基于CEEMD的滚动轴承振动信号自适应降噪算法。
2.1 自相关函数单边波峰宽度
信号xt的自相关函数Rx(τ)反映了信号在不同时刻t1和t2取值的相关程度,常用的是归一化自相关函数:
(3)
τ=t1-t2表示时间差。
如图1所示,由于随机噪声在各个时刻表现出弱关联性和较大的随机性,其自相关函数曲线变化陡峭、曲线尖锐,具体体现在其自相关函数值在零点处最大,在其他点处会迅速衰减到极小值。对理想的高斯白噪声而言,它的归一化自相关函数值在零点处等于1,在其他点处等于0。一般信号在各个时刻都存在着较强的关联性,因此其自相关函数曲线变化缓慢、曲线平滑,虽然自相关函数值仍然在零点处取得最大,但在其他点处并没有迅速衰减到很小的值。
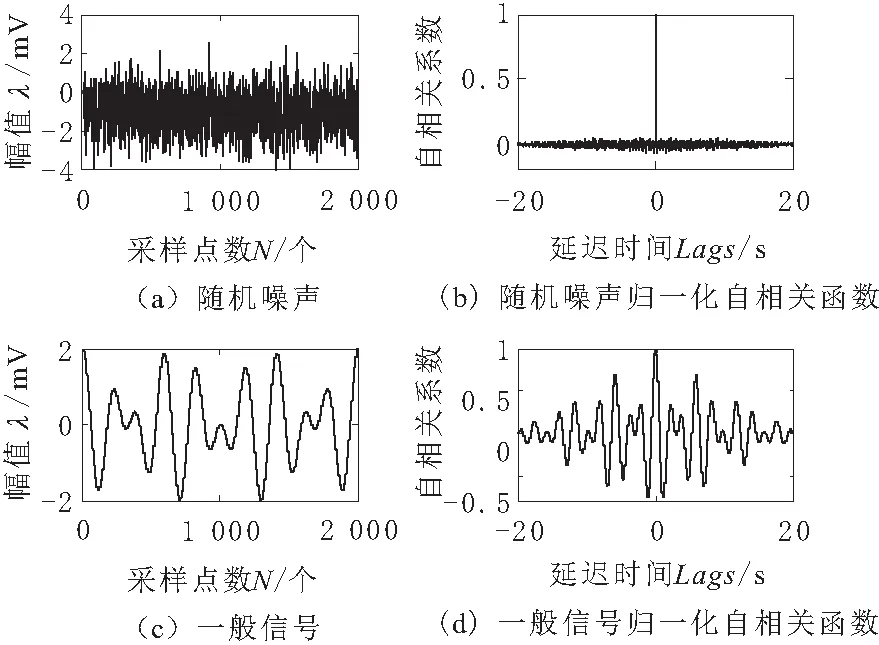
图1 随机噪声与一般信号及其归一化自相关函数
将CEEMD各IMF分量归一化自相关函数曲线的波形特点及其在各个时刻的函数值变化作为信噪分量分界点的判断准则,并不能保证重构的精度。在此基础上,本文采用归一化自相关函数曲线的单边波峰宽度来表征曲线的尖锐程度。由于ρx(τ)为实偶函数,关于纵坐标轴对称,因此将ρx(τ)的值从1降到0.5时所对应的宽度定义为单边波峰宽度[9]。若ρx(τ1)=1,ρx(τ2)=0.5,则归一化自相关函数曲线的单边波峰宽度定义:
d=|τ2-τ1|
(4)
为定量确定分界点,进一步计算单边波峰宽度与最大延迟时间τmax的百分比,称为峰宽占比。
(5)
将图1中的随机噪声与一般信号相叠加得到仿真信号,计算仿真信号IMFs归一化自相关函数的单边波峰宽度与峰宽占比,可以得到如图2所示的单边波峰宽度与峰宽占比的变化规律曲线,从图2中可以看出,随着分解尺度的增大,IMFs分量归一化自相关函数单边波峰宽度整体上呈增大的趋势,且增大的速度越来越快,并且前五阶IMF分量归一化自相关函数的波峰宽度很小,均小于0.04,峰宽占比λd<0.5%。
根据仿真信号归一化自相关函数曲线单边波峰宽度与峰宽占比的变化规律,设定峰宽占比的临界值为0.5%,即将λd<0.5%对应的IMF分量视为噪声分量,第一个满足λd≥0.5%且其后的峰宽占比呈递增趋势的IMF分量所对应的阶数即为信噪分量的分界点。
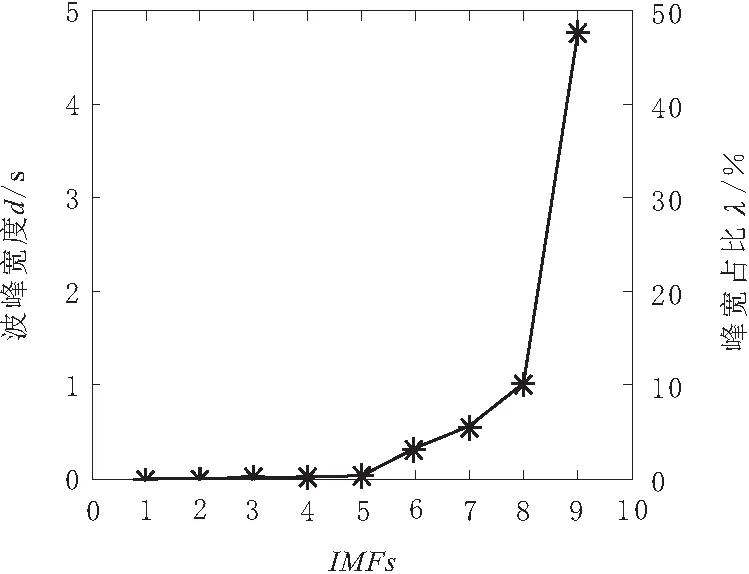
图2 IMFs归一化自相关曲线波峰宽度与峰宽占比
2.2 阈值函数的改进
小波阈值降噪的基本原理是对信号进行多层小波分解,得到近似系数和细节系数。确定阈值后利用阈值函数对小波系数进行处理,接着对阈值化后的小波系数进行重构即完成降噪过程。滚动轴承振动信号经小波分解后,一般认为大于阈值的小波系数重构后为有效信号,小于阈值的小波系数重构后为噪声。小波阈值处理的好坏直接影响信号降噪的最终效果。传统的小波阈值函数主要包括硬阈值函数和软阈值函数[10],表达式为:
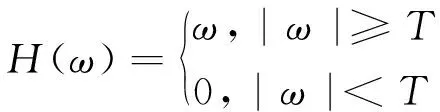
(6)

(7)
T为设定的阈值;ω为原始信号的小波系数;H(ω)为硬阈值函数处理后的小波系数;S(ω)为软阈值函数处理后的小波系数。
硬阈值函数和软阈值函数各有其优势,但存在间断点和信号失真等问题。本文提出的改进阈值函数对两种函数的缺陷进行了弥补,表达式为:
(8)
a>0,b>1;I(ω)为改进阈值函数处理后的小波系数。T1,T2表示设定的阈值,T2=bT1,T1可由下式计算得到[11]:
(9)
N为采样点数;σ为第k层噪声的标准差,可按下式进行估算:
(10)
median(|ω|)表示第k层分解小波系数的绝对值取中值。
调整改进阈值函数中的参数a,b就可以使函数达到不同的效果。3种阈值函数如图3所示,横坐标为原始信号的小波系数,纵坐标为经过阈值函数处理后的小波系数,且均为无量纲参量。
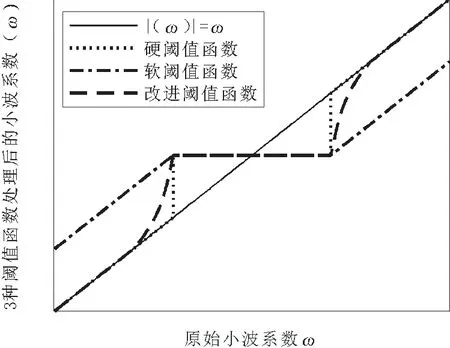
图3 3种小波阈值函数对比
2.3 基于CEEMD的振动信号自适应降噪算法
应用信号自相关函数单边波峰宽度特性与改进的小波阈值函数,提出的基于CEEMD的滚动轴承振动信号自适应降噪算法具体步骤如下:
步骤一,对原始信号x(t)进行CEEMD分解,得到信号的各阶IMF分量IMFj与残余分量。
步骤二,画出各IMF分量的归一化自相关函数曲线。
步骤三,根据各IMF分量自相关函数曲线,计算对应的单边波峰宽度和峰宽占比。根据设定的λd≥0.5%判断有用信号分量与噪声分量的分界点j。
步骤四,对分界点前面的j-1个IMF分量进行改进小波阈值降噪,以获得其中的高频有效信息。
步骤五,将降噪后的IMF分量与剩下的IMF分量以及残余分量进行重构,完成降噪过程。
3 实验分析
将本文所提出的降噪方法应用于滚动轴承内圈故障振动信号的分析。数据来自于美国西储大学实验平台,该平台包括1个1.5 kW的电机,1个转矩传感器,1个功率计和电子控制设备。实验中使用加速度传感器采集振动信号。选用型号为6250-2RS JEM SKF的轴承作为实验对象,被测试轴承支承电机轴。该轴承的基本参数为:内圈直径25 mm,外圈直径52 mm,节径39.039 8 mm,滚动体个数9个,滚动体直径7.937 5 mm,接触角为0°。使用电火花加工技术在轴承内圈上布置单点故障,故障直径为0.035 56 cm,深度为0.027 94 cm。采样频率12 kHz,电机转速1 772 r/min。
根据式(11)可以得到该实验轴承的内圈故障频率fi为157.92 Hz。
(11)
n为转速;Z为滚珠个数;d为滚动体直径;D为轴承节径;α为接触角。
图5为滚动轴承内圈故障振动信号的时域波形图,采样点数为1.2×104,时间为1 s。对该信号进行CEEMD分解,得到10个IMF分量与1个残余分量。图6为IMFs分量归一化自相关函数曲线的单边波峰宽度与峰宽占比变化规律曲线,表1为各IMFs分量对应的峰宽占比计算数据。
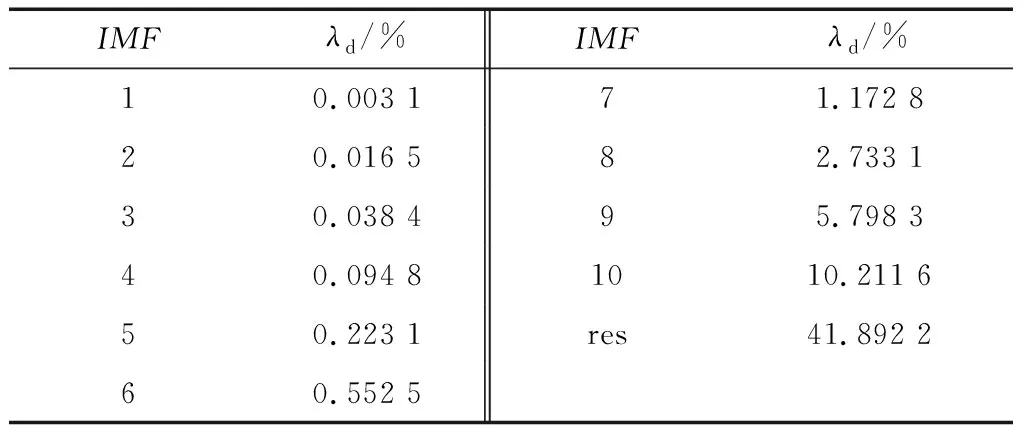
表1 振动信号IMFs自相关函数曲线峰宽占比
根据设定的判断准则λd≥0.5%,结合图7和表1可以判定CEEMD信噪分量的分界点为IMF6。从图7中可以看出,从第五阶IMF分量开始,归一化自相关函数单边波峰宽度突然增大并急剧上升,验证了以λd≥0.5%为准则判断CEEMD信噪分量分界点的有效性与合理性。

图5 滚动轴承故障振动信号
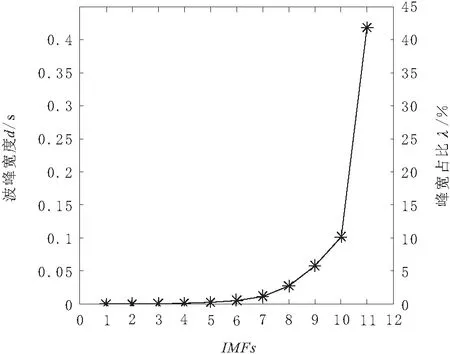
图6 振动信号IMFs自相关曲线波峰宽度与峰宽占比曲线
为了验证本文降噪方法对滚动轴承故障振动信号降噪的可行性与有效性,将本文方法的降噪结果与 CEEMD强制降噪、小波阈值降噪的结果进行对比。在使用本文降噪方法和CEEMD强制降噪方法时,对筛选出的信噪分量进行不同的处理。3种降噪方法对滚动轴承故障振动信号的降噪效果如图7所示。从图7中可以看出,滚动轴承故障信号经3种方法降噪处理后,噪声均得到了明显的抑制。由于CEEMD强制降噪完全丢弃了高频IMF分量,使得重构后的信号不完整,故障信息也因此丢失。传统小波阈值降噪方法和CEEMD改进小波阈值降噪方法的重构信号都具有非常明显的周期性冲击,两者仅从波形上看相差不大,因此继续对重构后的信号做快速傅里叶变换,得到的频谱如图8所示。
本次实验所用到的轴承的内圈故障频率fi为157.92 Hz,分析振动信号与降噪信号的频谱图可以发现,CEEMD强制降噪方法将高频IMF分量和有效信息一并丢弃,只保留了振动信号中的低频部分。传统小波阈值降噪方法虽然保留了有效信息,但降噪不彻底,使得有效信息和一部分高频噪声重叠在一起。CEEMD改进小波阈值降噪方法不仅有效滤除了高频噪声,频谱图中最大幅值所对应的频率为159.7 Hz,这与理论上计算的滚动轴承内圈故障频率157.92 Hz相差很小,验证了该方法的有效性与可行性。
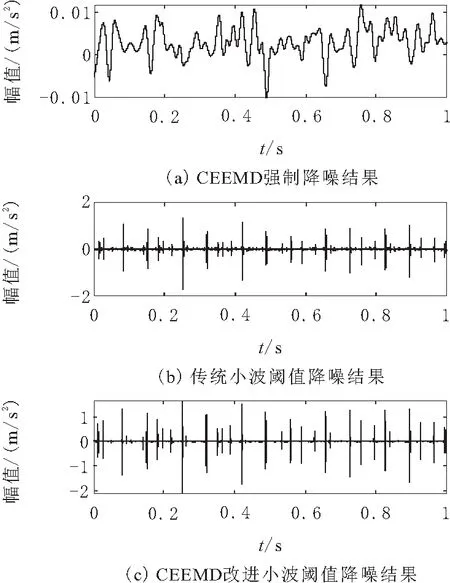
图7 3种降噪方法的降噪效果对比
4 结束语
CEEMD方法能够有效抑制模态混叠现象并提高计算效率。在应用CEEMD降噪时,在信号自相关函数特性的基础上,设计了依据自相关函数单边波峰宽度与峰宽占比自适应确定CEEMD信噪分量分界点的方法。为了保证重构信号的完整性,进一步采用改进的小波阈值降噪方法提取高频IMF分量中的有效信息。通过应用本文方法对滚动轴承内圈故障振动信号降噪,得到降噪后信号的故障频率为159.7 Hz,与理论计算的故障频率157.92 Hz相差较小,验证了该方法的有效性和可行性,为滚动轴承振动信号降噪提供了一种新方法。

