基于某种生物启发式算法的无人机航迹规划
,,, ,
(南京航空航天大学自动化学院,江苏 南京 211106)
0 引言
无人机航迹规划是指在一定的约束条件限制下,按照某种评价标准寻找从起点到目标点的最优路径[1]。航迹规划过程中最为核心的内容就是航迹规划算法,针对无人机航迹规划算法,国内外许多学者做了大量的研究,具有代表性的航迹规划算法有:A*算法、动态规划法、人工势场法、遗传算法、粒子群算法、人工蚁群算法等,这些算法都有其各自的特点,但是也存在缺点与不足。对于无人机航迹规划,通常会根据具体的情况,结合实际应用对算法进行改进,如郭忠同、扈宏杰[2]等人针对人工势场法易陷入局部最优的缺点,提出了改进后的算法,将其应用于航迹规划中,提高了算法的收敛速度;于霜[3]等人针对传统人工蜂群算法常见的缺点,提出用自适应搜索机制、一种新的概率选择方式和混沌搜索策略对算法进行改进;刘丽峰[4]等人以人工免疫算法为基础,针对算法搜索效率差的缺点,对算法进行了改进。这些经过改进之后的航迹规划算法,在一定程度上提高了算法寻优速度,但是依旧存在很多不足:如算法的通用性较差,容易陷入局部最优等。
针对上述问题,本文提出一种樽海鞘群智能算法(salp swarm algorithm,SSA),该算法模拟了海洋生物樽海鞘在海洋中导航和觅食时的群集行为。算法通过随机初始化种群解,选用合适的适应度函数进行个体评价,根据位置更新策略进行迭代,最终得到最优解,SSA算法具有良好的全局搜索能力和快速收敛的特点。同时,本文对威胁空间进行了建模,选取了合理的评价函数,通过仿真实验,验证了算法的优越性。
1 约束条件与威胁建模
无人机在执行任务的过程中,需要综合考虑各种因素,包括飞行区域的地形信息、威胁信息、飞行限制和无人机自身性能等内容[5]。因而在无人机航迹规划时,需要对约束条件和各类威胁进行分析与建模,通过评估综合代价,得到指标函数最优的航迹。
1.1 约束条件
1.1.1 最短航迹段
无人机在某些航迹段飞行时,需要一定的时间调整姿态,以便到达下一个指定位置时完成机动动作。为了保证飞行安全与质量,无人机在飞行姿态调整时的前后一段距离,需要直飞,直飞的这段距离为最小步长,记作lmin,则飞行过程中任意航迹段都不能小于最小步长,如式(1):
li≥lmin,(i=1,2,,n)
(1)
1.1.2 最大航程限制
无人飞行器的最长飞行距离受其所携带的燃料量限制。在从起点飞向终点的过程中,无人机需要回避障碍物与威胁,由于燃料有限,为保证飞行安全,必须将航程限制在一定的范围内。假设最大航程为lmax,一条航迹分为n个航迹段,li表示第i个航迹段,则总航程满足以下约束:
(2)
1.1.3 最大转弯角限制
无人机受机动性能限制,其转弯角和爬升/俯仰角不能过大,本文是在二维环境下对无人机航迹规划进行研究的,因此只考虑无人机飞行时的最大转弯角。在无人机航迹规划时,每个航迹段之间的夹角都不能大于预先设定的最大转弯角。
如图1所示,θ为最大转弯角,假设第i个航迹点坐标表示为(xi,yi),i-1个航迹点坐标表示为(xi-1,yi-1),则第i条航迹段表示为ai=(xi-xi-1,yi-yi-1),该约束可表示为:
(3)
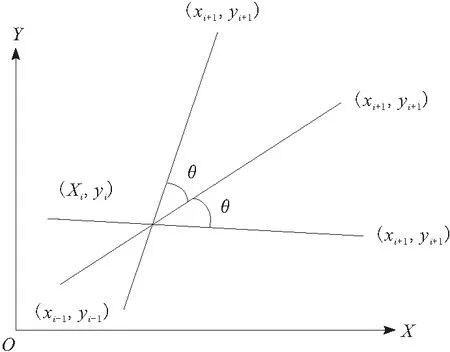
图1 最大转弯角
1.2 威胁建模
1.2.1 山峰威胁
无人机飞行过程中受地形因素影响,而山峰是主要地形因素,对于单个山峰地形来说,可以用如下表达式来模拟:
(4)
z0为山峰地形的基准高度;(x0,y0)表示山峰的中心坐标;a,b反映x轴,y轴方向地形衰减速度,衰减越快则该轴地形越陡峭。本文假设无人机以固定高度飞行,即Z(x,y)为常数,则山峰影响区域可以用圆形表示,无人机不能在圆形区域内飞行,obs表示无人机受山峰威胁的区域范围,其表达式如下:
obs={(x,y)|(x-x0)2+(y-y0)2≤max(a,b)2}
(5)
1.2.2 雷达威胁
雷达是军事作战中的重要装备,其主要是利用电磁波理论,通过接收目标反射的回波信号进行探测,雷达是否能截获目标取决于接收信号的质量,简化的雷达接收功率方程为[6]:
(6)
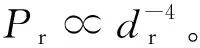
(7)
一条航迹共有n个航迹段,则整条航迹受到的雷达威胁可表示为:
(8)
经过对山峰威胁和雷达威胁的分析,可以发现,山峰威胁可以近似用雷达威胁模型反映,将山峰模型用与雷达相同的量化方式进行量化,则第i条航迹对于威胁源j的代价可表示为:
(9)
假设飞行过程中有m个威胁存在,则总的威胁代价为:
JT=JT,1+JT,2++JT,m
(10)
1.3 航迹代价评价指标函数
综合无人机飞行的约束条件和执行任务可能面临的威胁,可得到无人机航迹规划的代价函数,代价函数需要反映出航程长短、避开威胁的程度、时间长短等指标。航迹代价评价函数如下:
J=ωJL+(1-ω)JT
(11)
J为航路的总代价值;ω为代价权重系数,其大小根据实际规划需要确定;JL为航程代价,JL=Li,即第i条航迹的总长度,总长度越长航程代价值越大;JT为威胁代价。
2 SSA算法
2.1 算法描述
SSA算法模拟了海洋生物樽海鞘在海洋中导航和觅食时的群集行为。樽海鞘的身体呈桶状,身长在1~10 cm范围,是一种远海胶质脊索动物,它们靠不断吸入和喷出海水在海里完成移动。樽海鞘有一个显著的行为,是它们的蜂拥行为,这种行为主要是由于樽海鞘可以通过快速协调的改变和觅食来实现更好的运动。在SSA算法中,解群相当于樽海鞘群,樽海鞘位置变化的过程相当于解群不断更新的过程。
为了解决寻优问题,本文提出樽海鞘链模型[7]。樽海鞘群中有两种类型的个体:领导者和追随者。领导者会直接或间接的引导链条中追随者的运动。一个由M个樽海鞘组成的樽海鞘链X可以由一个二维矩阵表示,这个群体的目标是搜索空间中的一个食物来源,记作F。
(12)
SSA算法的数学描述为:设樽海鞘搜索的区域是一个N维空间,一个群体中有M个樽海鞘,其中第i个樽海鞘的位置x表示优化问题的其中一个解。每个樽海鞘个体会按照一定的规则不断调整自己的位置,最终寻得最优解,每个樽海鞘都有一个由被优化函数决定的适应度值,根据适应度值计算函数可以求出目前为止整个樽海鞘群发现的最好位置,在N维空间中,每次迭代之后,都会存在一个目前为止整个樽海鞘群发现的最好位置,记为g=[g1,g2,,gN],gd表示在d维分量中的最优解,将gd作为d维分量中的食物源Fd,即群体目标随迭代次数而更新。则第d维分量中,作为领导者的樽海鞘位置变化公式为:
(13)
k表示迭代次数;c1是一个在迭代过程中逐渐减少的变量,并按照下列方程计算:
(14)
l和L分别是当前迭代和最大迭代次数。c2和c3是[0-1]之间的随机数,它们的取值决定了将第d个维度中的下一个位置指向正或者负以及指定步长。ubd,lbd分别代表d维分量中x的最大和最小边界。d维分量中,第i个跟随者位置变化公式为:
(15)
与其他群智能算法类似,SSA是一种基于群体的算法,并从随机初始化个体开始,每一个个体都代表解决目标问题的候选方案。SSA算法保存了迄今为止获得的最佳解决方案,并将其作为群体目标,保证了群体中解的优良性。算法只更新群体中领导者相对于目标的位置,领导者可充分利用和探索其周围的空间,此过程具有快速和随机的特点,从而增加了算法的寻优效率。在足够的探索后,群体中的跟随者会逐渐向领导者移动,此过程不如探索阶段的范围大,具有缓慢改变和局部移动的特点,可避免算法陷入局部最优。
2.2 规划空间
无人机航迹规划问题可描述为在给定的飞行区间内,寻找从起始点到达目标点的最优路径。为降低航迹规划问题的复杂性,首先需要对飞行环境进行规划和建立模型,本文提出一种操作简单、易于计算的方法来构建环境模型[8]。

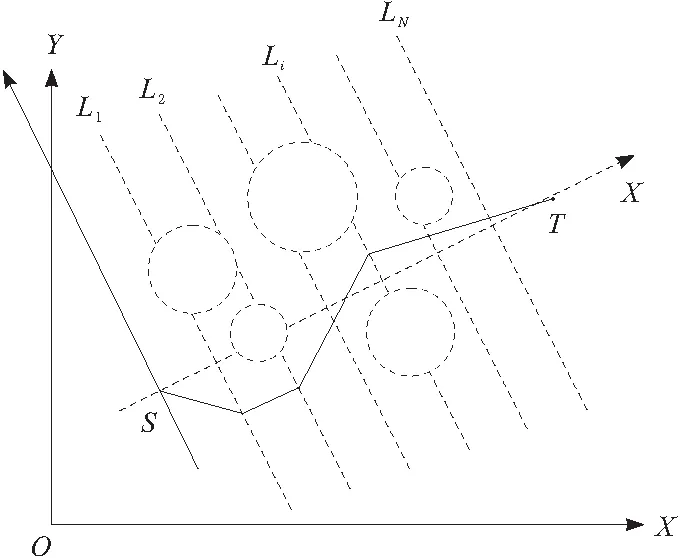
图2 路径的生成
2.3 适应度函数
适应度函数是衡量樽海鞘种群质量的重要依据,适应度函数的选取,是种群个体位置变换更新的基础,它对于算法的收敛性和快速性有着重要的影响,适应度函数是评价航迹好坏的指标。综合考虑无人机飞行过程的约束条件和威胁等影响因素,可得到适应度函数U(x)的公式:
U(x)=ε∞-J
(16)
ε∞是一个足够大的数;J为航迹总代价值,结合代价公式和适应度函数公式可以看出,航迹长度越短,航迹适应度函数U(x)越大,航迹段距离威胁越远,适应度函数越大。因此,该计算公式在满足约束条件要求下,可达到减小航迹长度和避开威胁的目的。
2.4 算法流程
SSA算法的基本流程[9]如图3所示。

图3 SSA算法流程图
3 仿真验证
3.1 仿真条件
本文设定了一个240 km×120 km的二维规划空间,设无人机飞行起始点位置为S,目标点位置为T,起点与目标点之间的直线距离为200 km,本文采用SSA算法和粒子群算法进行航迹规划,使用MATLAB R2014a进行计算和仿真分析。将整条航迹分为N+1段,取N=10,群体大小M取30,最大迭代次数L=100,代价权重系数ω取0.3,c1根据公式(14)计算,c2和c3取[0-1]之间的随机数,ub,lb为y的最大和最小边界,令ub=120,lb=0,最大转弯角度设为±45°,最大航程为400 km。
3.2 仿真结果与分析
如图4和图5所示,取无人机飞行起点作为二维坐标系的原点;三角形代表无人机要到达的目标位置;灰色圆形表示雷达区域;黑色圆形表示山峰区域;黑色线段表示规划出的无人机最优路径。仿真结果证明,采用SSA算法和粒子群算法各运行100次后,两种算法都可以找到各自的最优路径。对比图4和图5可以看出,针对复杂环境,SSA算法可充分利用威胁模型,规划出较短路径,并且可以保持较小的转弯角度,更好的体现了SSA算法的快速收敛性和鲁棒性,相比之下,粒子群算法所规划出的路径航程较长、耗时多,转弯角度也偏大。
如图6所示,利用MATLAB对所建立的适应度函数进行验证,黑色实线表示SSA算法的适应度值变化趋势,虚线表示粒子群算法的适应度变化趋势。由此可以看出,利用SSA算法求解时,算法收敛时适应度值为140,而运用普通的粒子群算法时,算法收敛时适应度函数值为80。显然,SSA算法的寻优速度和寻优效果都要比粒子群算法好。

图4 基于SSA算法的无人机航迹规划

图5 基于粒子群算法的无人机航迹规划
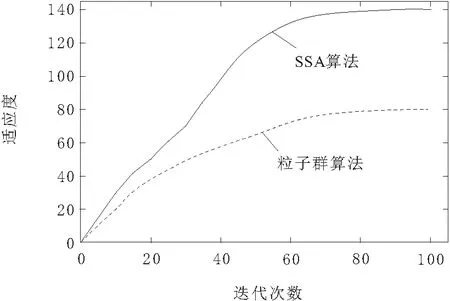
图6 适应度收敛图
如图7所示,基于两种算法规划的路径长度均随迭代次数不断变化。从图中可以看出,在基于粒子群算法的航迹规划中,最短航迹近似为260 km,收敛次数约为80,收敛区间为258~262 km。而在基于SSA算法的航迹规划中,最短航迹近似为210 km,收敛次数约为60,收敛区间为209~211 km。
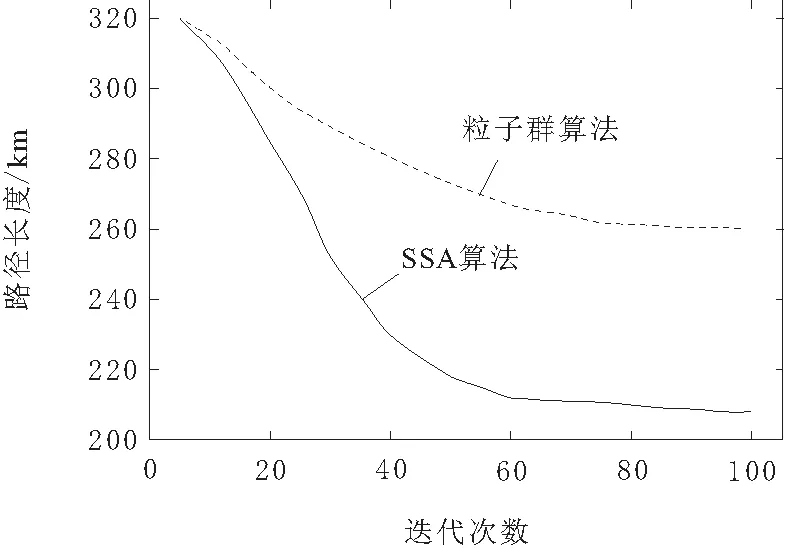
图7 路径长度随迭代次数变化图
4 结束语
本文研究了复杂环境下的无人机航迹规划问题,首先分析了飞行过程中的约束条件,建立了山峰、雷达等各类威胁模型,为算法选取了合适的适应度函数;对飞行区域进行了合理的规划,通过SSA算法,求解无人机最优路径。该算法通过位置更新策略来更新群体状态,增加了种群的多样性和寻优效率,与传统算法相比,SSA算法可避免局部最优,具有很好的全局收敛性。但本文只是考虑了二维空间中无人机航迹规划问题,并未涉及三维空间。为了使无人机更好的适应作战环境,如何将SSA算法应用到无人机三维航迹规划问题中,将是未来需要深入研究的问题。

