基于贝叶斯网络的MEC随机任务迁移算法
薛 宁 霍 如 刘 江
1 北京工业大学北京未来网络科技高精尖创新中心 北京 100124
2 北京邮电大学网络与交换技术国家重点实验室 北京 100876
引言
近年来,移动互联网和物联网两大网络得到了快速发展,对网络的时延、可靠性提出了更高的要求,而移动边缘计算(Mobile-edge Computing,MEC)由于其靠近用户的特性,可以为用户提供更低时延、更可靠的网络体验[1]。在移动边缘计算的场景下,用户和服务器的距离很近,数据的传输速率会很快,在处理任务时既可以利用服务器强大的计算能力又可以节省移动设备的资源消耗。因此,移动设备更倾向于向MEC服务器迁移任务从而提高任务的执行性能,降低任务在移动设备上的开销。这种变化使得移动设备计算任务的迁移算法变得十分重要。
学术界在任务迁移方面有一定的研究成果,文献[2]将一个应用划分为一组有数据依赖关系的子任务,通过将子任务间共同需要的数据在移动端和服务器各存一份的方式来减少传输能耗。但是,在真实环境中是无法预知子任务间共同需要的数据的。文献[3-5]则提出对多个随机任务的调度迁移策略进行优化,利用MDP理论、Lyapunov优化算法以最小化移动设备能耗和执行时延为目标来决策调度策略。然而在真实场景中部分任务需要和移动设备进行交互而必须在本地执行,并且子任务之间是存在关联性的,使得调度策略无法达到能耗和时延最小化的目标。所以本文首先将应用转换为包含多个子任务的有向图,从而表征应用本身子任务间的内在联系,在此基础上提出了一种基于贝叶斯网的随机任务迁移算法,利用子任务之间的依赖关系预估每一个子任务执行两种迁移决策所产生的能耗,并得出每个子任务执行两种迁移决策的先验概率,最后根据先验概率以移动设备能耗最小化为优化目标生成一组调度策略。
1 系统模型
本文考虑的MEC系统模型如图1所示,包含一个移动设备和一个MEC服务器。移动设备是由迁移决策单元、本地处理单元和传输单元组成,移动设备通过传输单元将一些计算密集型的计算任务迁移到MEC服务器上执行,以解决移动终端计算能力有限的问题。MEC服务器是一个部署在无线接入点处并安装了小型数据中心的虚拟机设备,可以为移动设备提供强大的IT服务[6]。
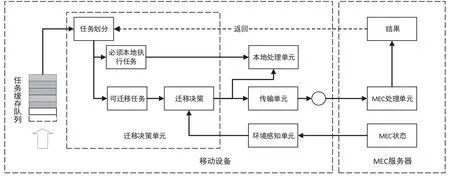
图1 单用户MEC系统场景图
1.1 任务模型
图2所展示的是一个应用的细粒度任务划分图,本文将应用划分为多个独立执行的子任务,并用一个有向图来表示[2]。图2中的节点表示分割出来的子任务,图2中的边表示任务之间的传输数据,例如:表示任务执行完成后,会传输的数据给任务而任务只有在接受到任务执行完后传输过来的数据,才能开始执行。图2中的子任务可以分成两类:一类是必须本地执行的任务,如图中的实心任务0、5表示为另一类为可迁移任务,如图中的空心任务1、2、3、4,表示为

图2 细粒度任务划分图

1.2 计算模型
由于执行任务的能耗与任务在移动设备执行还是被迁移到MEC服务器执行有关,所以本文定义表示任务执行位置:

由于执行任务的能耗与该任务的前置任务的执行位置有关,当此任务及其前置任务都在同一位置执行时,两个任务之间的数据传输消耗可以忽略不计。所以本文定义表示一个任务的前置任务的执行位置和该任务的执行位置:

假设移动设备配备单核CPU和一个数据传输单元,执行任务时CPU的频率为其功率为空闲时CPU的功率为数据传输单元发送功率为发送速率为接收功率为接收速率为MEC服务器执行任务时CPU的频率为为任务的计算量,单位为(CPU cycles)。表示任务执行完成后,会传输的数据给任务,单位为(bites)。









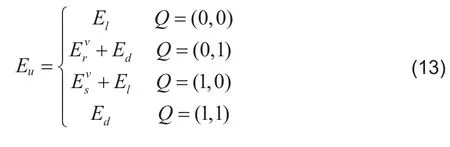
本文通过优化任务调度的迁移策略来最小化执行能耗,从而节约移动设备的能耗。
2 随机任务迁移算法
本节提出一种基于贝叶斯网络的任务迁移算法,根据子任务之间的依赖关系构造贝叶斯网,并求出最小化能耗的迁移策略。
2.1 贝叶斯网络
贝叶斯网络结合了图论、概率论以及机器学习等理论和技术,是以有向无环图的形式建模。用节点表示系统中的变量,用有向边表示变量间的依赖关系。
贝叶斯网络可以通过图形化的方式对变量间的定量依赖关系进行描述,在联合概率分布中给各个变量均赋予一个特定值于是利用贝叶斯网络中的各个节点所对应的条件概率分布表,将所需的其他概率信息计算出来[8]。表示概率,则有:
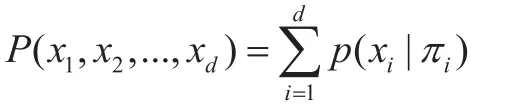
贝叶斯网络中节点之间的依赖关系由条件概率函数决定。每一个没有父节点的节点都有一个先验概率分布。这些节点都具有各自的边缘概率表,该边缘概率表显示相应节点独立的概率分布。边缘概率表中的概率数值表示了相应节点处于各个状态的概率。每一个边缘概率表中所有概率数值的和都为1。
每个具有父节点的节点都有相应的条件概率函数,该条件概率函数表示父节点和子节点之间的条件概率关系。两个节点之间的条件概率关系由条件概率表表示。条件概率表为子节点变量在给定父节点变量情况下的概率情况。
当贝叶斯网络建立后,通过一定的计算,可以获得贝叶斯网络内变量之间的依赖关系以及变量的概率分布。由此,依据贝叶斯网络中节点间的依赖关系以及变量的条件概率表,可以获得联合概率分布。此外,使用贝叶斯推理,可以利用已知的变量,通过贝叶斯网络中节点间的连接,计算出其它未知变量的信息[8]。
2.2 基于贝叶斯网络的迁移算法
根据应用的任务划分图构造一个贝叶斯网,每个子任务作为贝叶斯网的一个节点,根据子任务间的依赖关系构造贝叶斯网中各个节点之间的依赖关系。在贝叶斯网中可将不可迁移任务对可迁移任务的调度决策的影响转换为依赖前置任务的本地执行概率和依赖后置任务的本地执行概率,即当某个子任务属于不可迁移子任务,在对该子任务的前置子任务和后置子任务(均属于可迁移子任务)做调度时,考虑后置任务的执行位置是更有利于得出最优调度策略的。
当任务v有前置任务u时,任务v和任务u的条件概率表分别如表1和表2所示。

表1 任务的条件概率表
表2 任务的条件概率表

表2 任务的条件概率表
根据构造的贝叶斯网络的依赖关系可以得出贝叶斯网的联合概率:

由于有的任务被设定为必须在本地移动设备上执行的任务,所以图2中的任务0、5可以表示为其他任务则利用联合概率计算出每个任务在本地移动设备执行的概率,以任务1为例,其依赖前置任务时在本地执行的概率为:

利用动态规划对上式进行化解得:

任务1依赖后置任务时在本地执行的概率:

利用动态规划对上式进行化解得:

当获得任务v在本地移动设备执行的前置和后置概率后,若本地移动设备执行的前置和后置概率之和大于MEC服务器执行的前置和后置概率之和,则任务v在本地移动设备执行,否则,则任务v迁移到MEC服务器执行,计算式如下:

至此,可获得一组次优的迁移策略,然后对这组次优迁移策略执行一种弱穷举算法,该弱穷举算法认为每一个位置的状态与其他位置的状态是不相干的,在进行穷举时,每次只改变某一个位置的状态,并且在下一次穷举时,上一次改变的状态要恢复原样。弱穷举算法是为了解决原算法陷入局部最优解的问题,通过改变每一个位置的状态来跳出局部最优解,并且弱穷举算法具有低复杂度的特点,使得算法的能耗并没有大幅增加。在本算法中执行弱穷举算法即依次在这组次优迁移策略中选择一个位置(该位置必须为可迁移任务所在位置),将其替换为相反的迁移策略,再计算其总能耗,最后在所得的结果中选择能耗最小的迁移策略为最终迁移策略。
根据上述的方法,对可迁移子任务逐个计算在本地移动设备执行的概率,并依据前置依赖和后置概率决定任务的执行位置,再通过弱穷举算法得出一组最小化能耗的最优迁移策略。在计算最优迁移策略时,需要遍历整个任务拓扑图,其时间复杂度为而通过穷举法遍历整个解空间来找到最优解,由于所有解的数量为个,故穷举法的时间复杂度为贝叶斯迁移算法的时间复杂度是常数级别的,而穷举法的时间复杂度却是指数级的。由此得出,贝叶斯迁移算法的时间复杂度远小于穷举法,极大地减小了计算量。
3 仿真结果
在本节中,对提出的算法在python环境中进行了编码实现并且通过仿真实验对其性能进行了评估。仿真场景是:一个移动设备,一个搭载MEC服务器的基站,它们之间通过无线网络连接。移动设备和MEC服务器参数如表3所示。
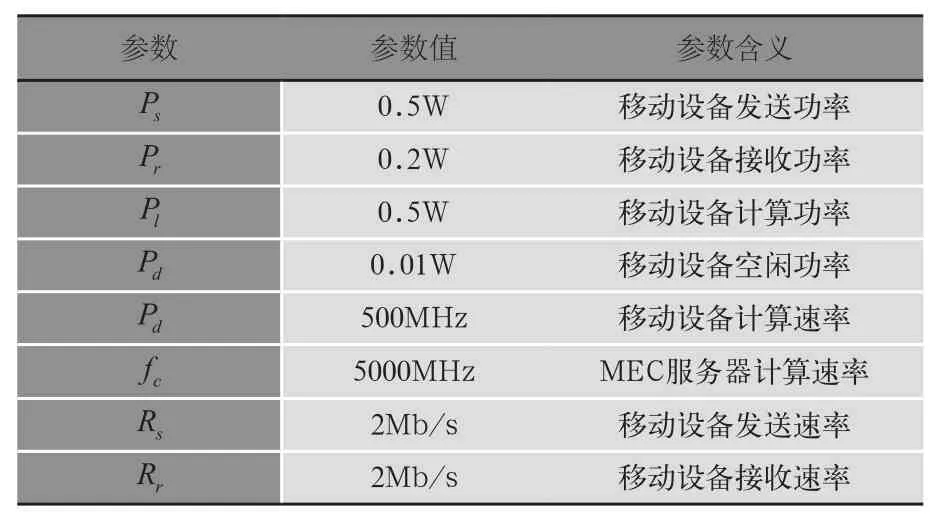
表3 移动设备和MEC服务器参数
为验证算法的有效性,引入3种基本的任务调度算法作为对比,包括随机任务随机迁移算法、MEC服务器迁移算法和移动设备本地执行算法[6]。与此同时,为验证算法鲁棒性,仿真中构建了10种不同的应用,这些应用的子任务数和子任务间的依赖关系均不相同,子任务构造如表4所示,并且任务子模块数据大小和任务的负载量服从均匀分布,即根据应用的子任务划分图,将每个子任务作为贝叶斯网中的一个节点,按照子任务间的依赖关系构造贝叶斯网中节点间的依赖关系。

表4 应用子任务构造表
图3展示了1000个任务在不同任务迁移策略下的能耗,从图4中可以看到随着任务数的增加,移动设备的能耗值呈线性增长,但是可以看到使用不同的迁移策略对能耗值的增加幅度的影响不同[10]。全部本地迁移策略由于其所有任务都在本地执行,所以它的总能耗值是最高的。全部服务器迁移策略由于其所有可迁移任务都在服务器执行,移动设备的能耗只有传输能耗,所以它的总能耗值小于全部本地迁移策略的总能耗值。随机迁移策略由于其迁移决策是随机的,对能耗产生的影响时好时坏,所以它的总能耗值介于全部本地迁移策略的能耗值和全部服务器迁移策略的能耗值之间。贝叶斯迁移策略所得出的迁移策略近似于最优解,所以它的总能耗值是最小的。
图4展示了1000个任务在贝叶斯迁移策略和穷举策略下的能耗,从图4中可以观察到在不同任务数下,贝叶斯迁移策略和穷举策略的能耗值是几乎重叠的。这说明了贝叶斯迁移策略虽然没有遍历整个解空间,但是最终得到的最优解和穷举策略得到的最优解基本一致,这也证明了贝叶斯迁移策略在降低时间复杂度的同时对能耗的优化效果没有损失。

图3 不同任务迁移策略能耗图

图4 贝叶斯迁移策略和穷举策略能耗图
4 结语
本文提出了在单用户MEC系统中基于贝叶斯网络的随机任务迁移算法,通过将应用转换为包含多个子任务的有向图,利用贝叶斯网络中对子节点的概率计算方法来计算当前子任务迁移决策的先验概率,然后根据概率以移动设备能耗最小化为优化目标生成一组调度策略,最后利用弱穷举算法对生成的调度策略进行调整来得出最佳的调度策略。该算法在一个随机任务到达时能够以常数级别的时间复杂度找到该任务的近似最优解,提高了优化效率。仿真结果表明,该算法对大量任务的迁移决策是非常有效的,使能耗得到了大幅度的减少。未来的研究工作主要包括加入对多任务能耗的优化、对移动设备无线信道传输功率的控制等。

