泌尿微创手术机器人结构设计及其运动学分析

陈林梓，管声启



泌尿微创手术机器人结构设计及其运动学分析

陈林梓，管声启*

（西安工程大学 机电工程学院，陕西 西安 710048）

传统泌尿微创手术时间长、医生劳动强度大，机器人的介入可有效提高该类手术效率、精准度及安全性.基于D-H参数法建立机器人运动学模型，进而对泌尿微创手术机器人进行正向运动学和逆向运动学分析，最后采用蒙特卡洛法在MATLAB软件中分析并生成机器人及其末端执行器的三维工作空间图.仿真结果表明，泌尿微创手术机器人结构设计合理且工作空间大，能够满足手术要求，为此类机器人的进一步研究奠定了一定的理论基础。

手术机器人；结构设计；运动学；蒙特卡洛法

0 引言

近年来，机器人技术逐步进入医疗领域并迅速发展成为一个新兴产业，微创手术机器人作为医疗机器人的一个分支也已成为研究的热点[1]，相比传统微创手术，手术机器人具有手术状态稳定、定位准确、灵活性好、工作范围大等优点[2-3]。微创手术机器人通过末端执行机构夹持手术器械并在合理的路径规划下将其伸入到人体内部，借助视觉显示系统的采样图像了解病灶信息并完成手术操作[4-6]，不仅有效滤除医生因疲劳而手颤、工作空间受限、操作难等不利影响因素，还大大降低了患者的痛苦、手术创伤及手术费用，利用手术机器人极大的提高了微创手术的效率、精准度、可靠性、操控性、稳定性[7-9]。

运动学分析可分为正向运动学与逆向运动学两部分，在手术机器人研究中占有重要地位，可为后续机器人工作空间分析及路径规划的研究打下坚实的基础[10-13]，同时，工作空间决定着机器人设计性能的好坏程度以及是否可以满足手术要求[14]。文献[15]对三指结构灵巧手进行了设计研究；文献[16-17]对微创手术机器人进行了运动学分析及建模仿真；文献[18-19]研究了手术机器人灵活工作空间的分布，尽管对微创手术机器人的研究很多，但它们都缺乏一定的针对性，不能满足具有特殊需求的手术过程。

为了使机器人能够代替医生夹持手术器械，并且在满足手术需求的条件下辅助医生顺利完成手术操作，本文设计了专门针对尿结石、前列腺肥大等泌尿类微创手术的机器人，以该手术机器人为例，通过采用D-H参数法建立运动学模型并进行运动学分析，然后利用MATLAB软件对其仿真，合理分析计算出符合泌尿类手术的工作空间。仿真结果表明，机械结构设计合理，建立的运动学模型正确，工作空间能够满足泌尿微创手术的要求。

1 泌尿微创手术机器人构型设计

泌尿类微创手术大多都是将手术器械经人体自然腔道插入，通过分析医生手部在手术过程中的动作可知，末端手术器械的运动可分为通过插入点沿自身中心轴的直线运动和转动、绕与插入点相切平面上两垂直轴线的转动，共有4个自由度，如图1所示，而要实现这样的运动，就需要手术机器人在整个手术过程中具有高灵活度，高稳定性，高精准度。

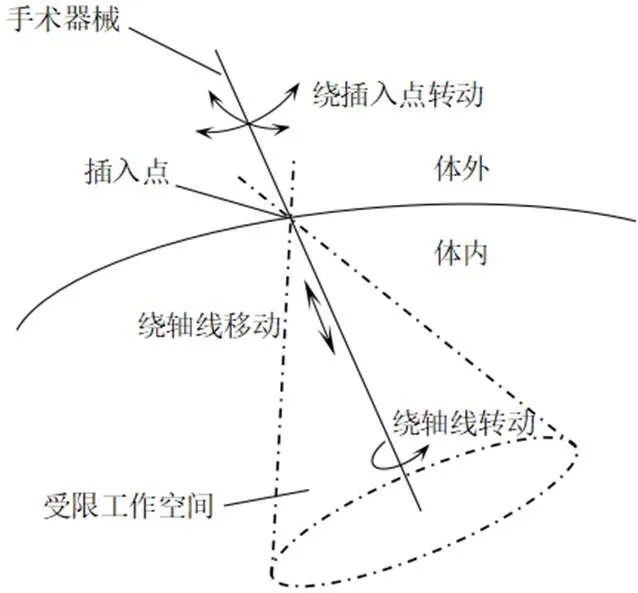
图1 手术器械工作示意图

通过对手术要求的分析，为解决医生因长时间手持器械而产生疲劳及工作空间狭小等问题，本文提出一种具有六轴六自由度的手术机器人，所有关节均为旋转关节，如图2所示。1、2、3关节为定位关节，决定机器人整体的位置，实现腕关节的定位，4、5、6关节为定向关节，用于调整末端手术器械的姿态，以适应不同的手术环境。其中关节1用于控制末端手术器械水平方向的位置，关节2与关节3用来调整末端手术器械的高度与进给量，以适应不同高度的手术台及患者不同的生理构造。当手术器械进入人体后，工作空间受自然腔道插入点的限制，1、2、3关节成为被动关节，此时为防止被动关节变化引起的末端手术器械工作幅度过大，从而导致人体内部正常组织及血管受到挫伤，可通过改变关节4、关节5来调整手术器械的姿态，保障手术安全。关节6主要使末端手术器械绕自身中心轴线转动，方便医生通过内窥镜了解病灶信息。

图2 泌尿微创手术机器人构型

2 运动学分析

2.1 D-H参数法建模

D-H参数法由Denavit与Hartenberg二人于1955年提出，是机器人学中有效表示机器人各杆件变化的经典方法。通过在机器人每个关节的坐标系建立4×4齐次变换矩阵来描述相邻杆件的位置关系，这样，通过矩阵的逐次变换，可以求出空间中末端执行器的坐标系相对于基坐标系的齐次变换矩阵[16]，从而得知末端位姿。根据图2所示泌尿微创手术机器人机构模型，采用D-H参数法建立以机座为参考坐标系的机器人运动学模型，如图3所示。

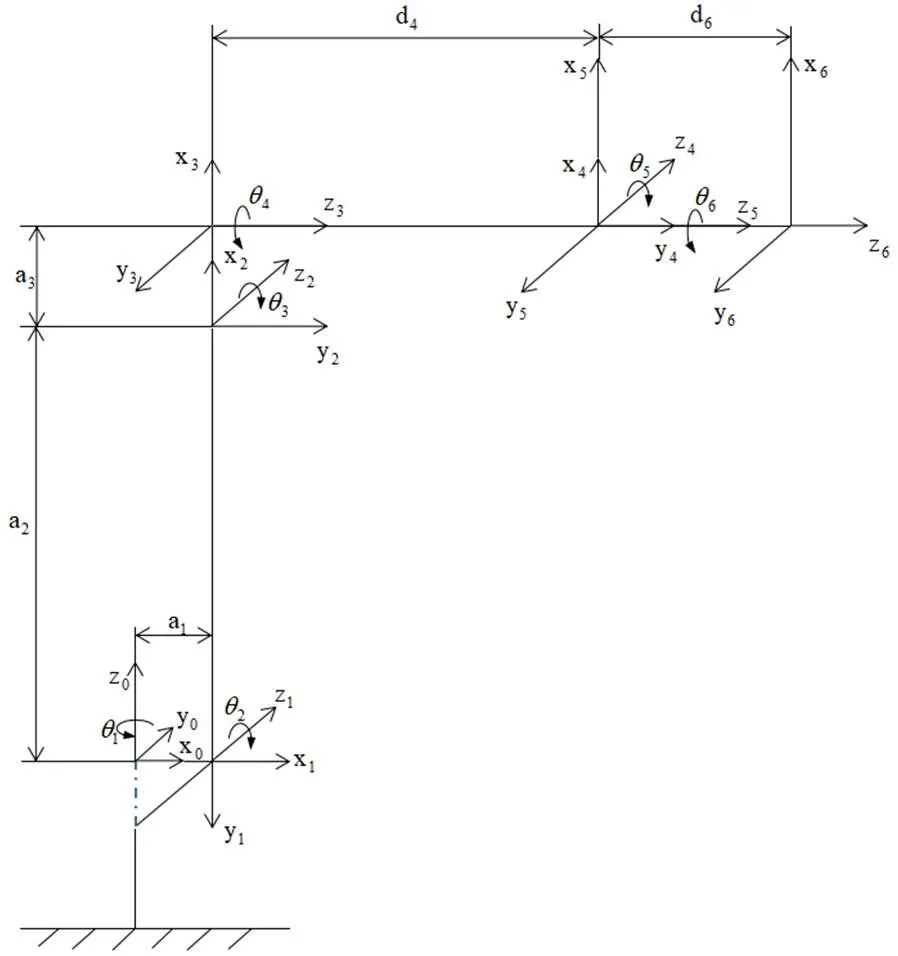
图3 泌尿微创手术机器人D-H坐标系

表1 D-H参数表

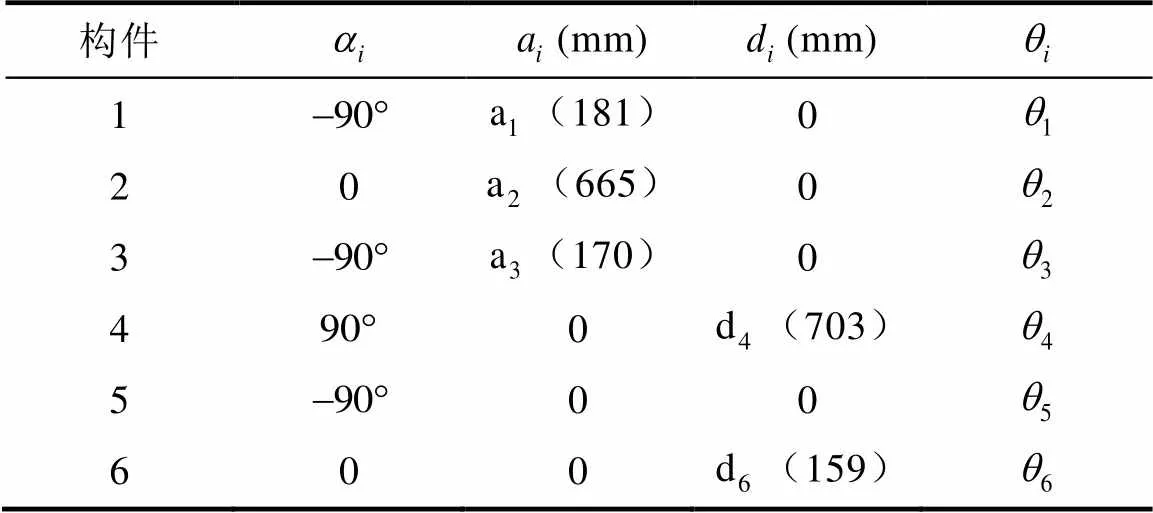
Tab.1 D-H parameter table

2.2 正向运动学分析

将表1中的参数代入式（1）中，即可求得各连杆坐标系间的齐次变换矩阵：

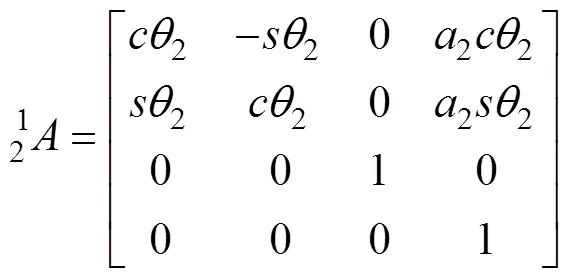
各变换矩阵连乘，得出泌尿微创手术机器人末端相对于基坐标系的位姿矩阵，如式（2）所示，其中为法向矢量，为方向矢量，为接近矢量，为位置矢量[20]。

n=s6*(c4*s1+s4*(c1*s2*s3–c1*c2*c3))+c6*(c5*(s1*s4–c4*(c1*s2*s3–c1*c2*c3))–s5*(c1*c2*s3+c1*c3*s2))

n=–s6*(c1*c4–s4*(s1*s2*s3–c2*c3*s1))–c6*(c5* (c1*s4+c4*(s1*s2*s3–c2*c3*s1))+s5*(c2*s1*s3+c3*s1*s2))

n=s4*s6*(c2*s3+c3*s2)–c6*(s5*(c2*c3–s2*s3)+c4*c5*(c2*s3+ c3*s2))

o=c6*(c4*s1+s4*(c1*s2*s3–c1*c2*c3))–s6*(c5*(s1*s4–c4*(c1*s2*s3–c1*c2*c3))–s5*(c1*c2*s3+c1*c3*s2))

o=s6*(c5*(c1*s4+c4*(s1*s2*s3–c2*c3*s1))+s5*(c2*s1*s3+c3*s1*s2))–c6*(c1*c4–s4*(s1*s2*s3–c2*c3*s1))

o=s6*(s5*(c2*c3–s2*s3)+c4*c5*(c2*s3+c3*s2))+c6*s4*(c2*s3 + c3*s2)

a=–s5*(s1*s4–c4*(c1*s2*s3–c1*c2*c3))–c5*(c1*c2*s3+c1*c3*s2)

a=s5*(c1*s4+c4*(s1*s2*s3–c2*c3*s1))–c5*(c2* s1*s3+c3*s1*s2)

a=s(2 + 3)*c4*s5 – c(2+3)*c5

p=a1*c1–d4*s(2+3)*c1+a2*c1*c2–d6*s(2+3)* c1*c5+a3*c1*c2*c3–a3*c1*s2*s3–d6*s1*s4*s5–d6*c1* c2*c3*c4*s5+d6*c1*c4*s2*s3*s5

p=–d4*(c2*c3–s2*s3)–a2*s2–d6*(c5*(c2*c3–s2* s3)–c4*s5*(c2*s3+c3*s2))–a3*c2*s3–a3*c3*s2

2.3 逆向运动学分析

逆向运动学问题即已知机器人末端的位置姿态，计算机器人对应位置的全部关节变量。逆解通常还是通过消元方法求解，但因为方程组为非线性超越方程，所以求解过程更为复杂，运算量大且解可能不唯一，或在某些点无解。

可求得：

其中，百联和阿里巴巴合作的案例中，百联包含连锁超市、购物商场等多种零售模式。从目前的形势上看，拥有近6 000家经营网点，并在2015年的时候，探究实体店铺O2O的升级与改造［8］。在 2016 年的时候，发布“i百联”全渠道电商平台，实现了线上线下业务的共同打造，满足了即时性的零售服务和体验。重构“人、货、场”等传统商业要素，并更好地为消费者和商户提供优质的物流服务。整合资源以实现线上线下协同发展，创新零售盈利模式，优化价值链网络体系，最终创新更多的企业价值。

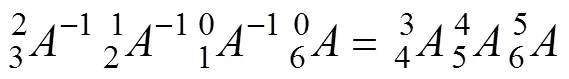
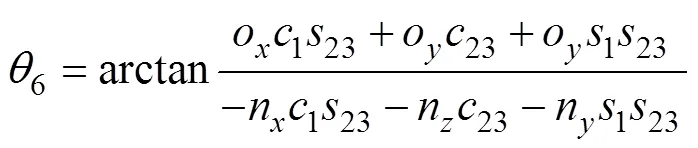
由以上结果可知，泌尿微创手术机器人的逆解存在多种情况，有些解是不能实现的，在此情况下，应当选取最优解以满足手术条件。

2.4 运动学模型仿真验证

根据表1中的参数，利用MATLAB中的Robotics Toolbox工具箱建立泌尿微创手术机器人的运动学模型，如图4所示。

在MATLAB环境下，任选几组关节角，分别将每组关节角输入到泌尿微创手术机器人正向运动学算法中，可以得到相应关节角下的机器人位置姿态；将正运动学位姿输入到逆运动学算法中，能够得到不同位姿所对应的六个关节角，再将这些关节角与任选的几组关节角对比，即可验证运动学解的正误。

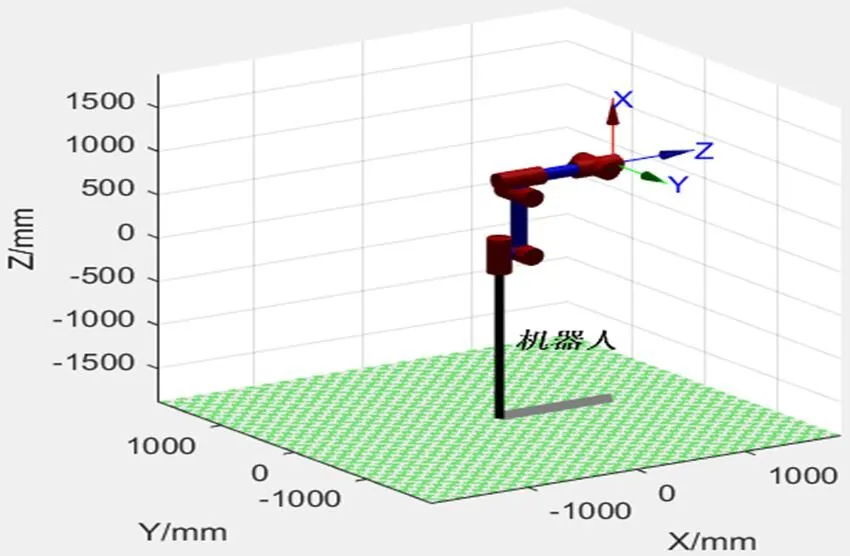
图4 运动学仿真模型

表2为任选的4组关节角，对应的末端位姿矩阵不在此列出；表3为相应末端位姿下的运动学逆解，通过对比表2、表3的关节角可知，在误差允许范围内，泌尿微创手术机器人的运动学正、逆解均正确。

表2 任选的几组关节角

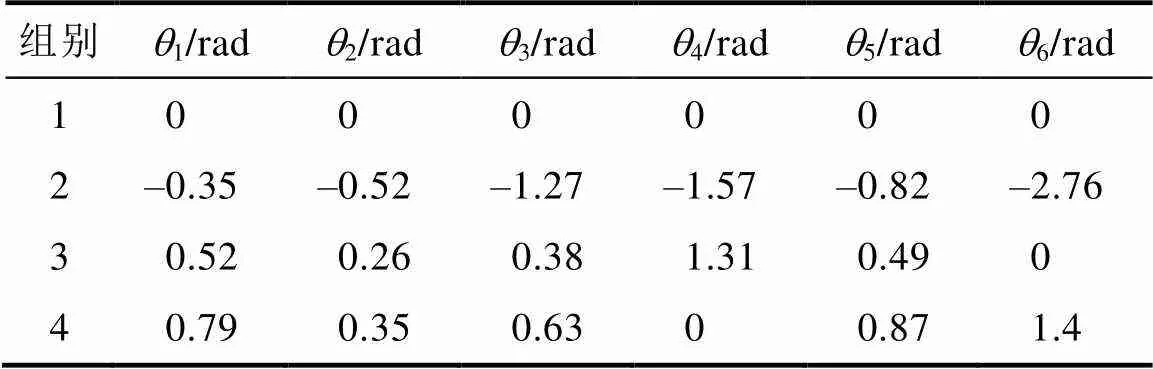
Tab.2 Selected sets of joint angles

表3 相应位姿下的运动学逆解

Tab.3 Kinematic inverse solutions under corresponding pose

3 基于蒙特卡洛法的运动空间分析

3.1 蒙特卡洛法

蒙特卡洛法是一种借助于随机抽样来解决数学问题的数值方法，广泛应用于工程、物理、经济等不同领域。采用蒙特卡洛法计算机器人工作空间，主要取决于机器人各关节变量范围，当所有关节变量在规定取值范围内随机遍历取值后，所有末端随机点的集合便形成机器人工作空间[21]，通过这种方法，可以方便的利用MATLAB软件将机器人工作空间显示出来。

3.2 整体工作空间分析

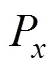
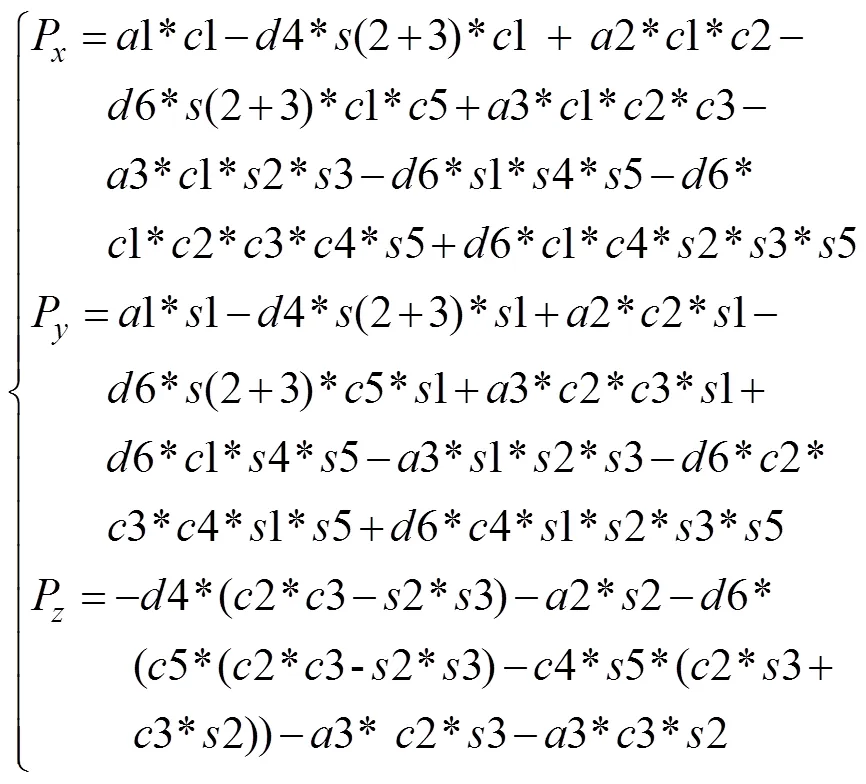
图6 XOY面

图7 XOZ面

图8 YOZ面

3.3 受限工作空间分析

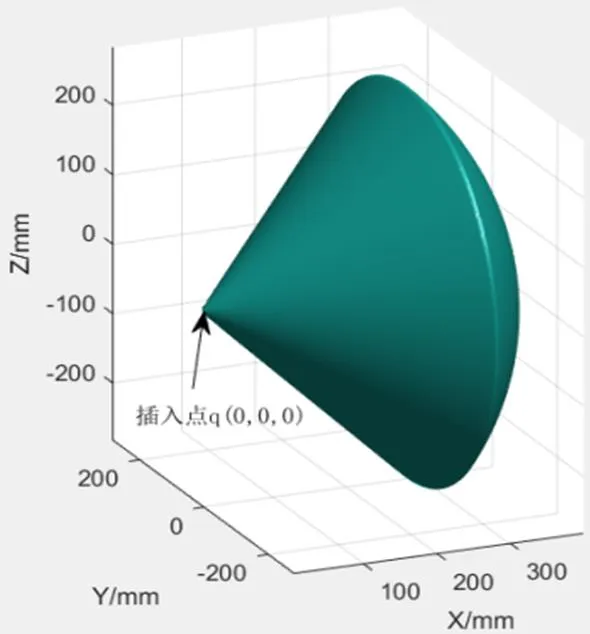
图9 受限工作空间

4 结语

本文针对医生长时间工作而产生疲劳、工作空间小等问题，研究了一种专门适用于泌尿类微创手术的机器人，通过D-H参数法建立运动学模型，求解机器人的正、逆运动学问题，并利用MATLAB软件中的Robotics Toolbox工具箱对机器人进行建模与仿真，验证了运动学解的正确性。基于正向运动学分析，采用蒙特卡洛法在MATLAB环境中对机器人整体工作空间以及受限工作空间进行分析。结果表明，泌尿微创手术机器人的构型设计可靠、运动学模型正确、工作空间合理，在理论上能够满足实际手术需求，为后续手术路径的规划及此类手术机器人的进一步研究奠定了基础。

[1] 林良明. 机器人辅助微创外科手术的发展[J]. 中国医疗器械信息, 2003, 9(2): 16-18.

[2] 唐实, 任淑霞, 王佳欣, 等. 基于虚拟VR技术的心脏医疗辅助系统的设计与应用[J]. 软件, 2018, 39(6): 23-25

[3] Munoz V F, Vara-Thorbeck C, DeGabriel J G, et al. A Medical Robotic Assistant for Minimally Invasive Surgery[C]// IEEE International Conference on Robotics and Automation. San Francisco, CA: IEEE, 2000: 2901~2906.

[4] 冯美, 付宜利, 潘博, 等. 腹腔微创手术机器人末端执行机构的设计和实现[J]. 机器人, 2009, 31(1): 47-52.

[5] Robinson T N, Stiegmann G V. Minimally Invasive Surgery[J]. Endoscopy, 2004, 36(01): 48~51.

[6] 郑华民. 微创外科的进展和发展趋势[J]. 中国实用外科杂志, 2002, 22(1): 16-17.

[7] 王振华, 洪鹰, 王国栋, 等. 主从式微创外科手术机器人主手设计[J]. 机械科学与技术, 2006, 25(5): 542-544.

[8] 杜志江, 孙立宁, 富历新. 机器人辅助医疗技术的新进展[J]. 高技术通讯, 2003, 13(6): 106-110.

[9] 吴俊. 六自由度双臂机器人动力学分析与运动控制[J]. 软件, 2017, 38(03): 128-132.

[10] 梁香宁. Delta机器人运动学建模及仿真[D]. 太原: 太原理工大学, 2008.

[11] 李慧霞, 高梓豪. 室内智能移动机器人规则物体识别与抓取[J]. 软件, 2016, 37(02): 89-92

[12] 伍经纹, 徐世许, 王鹏, 宋婷婷. 基于Adams的三自由度Delta机械手的运动学仿真分析[J]. 软件, 2017, 38(06): 108-112.

[13] 陈曦斌, 焦明海, 刘昊汧, 等. 移动机器人养老服务路径规划的粒子群算法研究[J]. 软件, 2018, 39(6): 135-138

[14] 单以才. 机器人机械操作臂的模块化设计及其控制的研究[D]．扬州: 扬州大学, 2003.

[15] 韦攀东, 李鹏飞, 王晓华, 等. 抓取柔软织物多指灵巧手的建模与仿真[J]. 西安工程大学学报, 2016, 30(3): 300-305.

[16] 哈乐, 王东辉. 基于D-H参数方法的微创手术机器人运动仿真研究[J]. 医疗卫生装备, 2014, 35(11): 19-21.

[17] 何志锋, 朱坚民, 宋成利, 等. 微创外科手术机器人运动学分析与研究[J]. 计算机仿真, 2014, 31(4): 412-415.

[18] 王汉飞, 刁燕, 罗华, 等. 微创手术机器人灵活工作空间的分析与优化[J]. 机械制造, 2016, 54(6): 23-25.

[19] 唐粲, 贠超, 栾胜. 一种新型医疗机器人运动学及灵活性分析[J]. 北京航空航天大学学报, 2005, 31(7): 748-752.

[20] 宋伟刚, 柳洪义. 机器人技术基础[M]. 第2版. 北京: 冶金工业出版社, 2015: 51-52.

[21] 蔡蒂, 谢存禧, 张铁, 等. 基于蒙特卡洛法的喷涂机器人工作空间分析及仿真[J]. 机械设计与制造, 2009(3): 161-162.

[22] 徐小龙, 高锦宏, 王殿君, 等. 基于MATLAB的七自由度机器人运动学及工作空间仿真[J]. 新技术新工艺, 2014(5): 21-24.

[23] 苑丹丹, 邓三鹏, 王仲民. 基于蒙特卡洛法的模块机器人工作空间分析[J]. 机床与液压, 2017, 45(11): 9-12.

Structure Design and Kinematics Analysis of Urinary Minimally Invasive Surgery Robot

CHEN Lin-zi, GUAN Sheng-qi*

(School of Mechanical and Electrical Engineering, Xi´an Polytechnic University, Xi´an 710048, China)

Traditional minimally invasive surgery of urology takes a long time and doctors work hard. Interventional robot can improve the efficiency,precision and safety of this kind of surgery effectively.The kinematics model of robot was established based on D-H parameter method.Then the forward kinematics and reverse kinematics of the Urinary Minimally Invasive Surgery Robot were analyzed.Finally,Monte-Carlo method is used to analyze and generate the the robot and 3-D workspace diagram of its end-effector in MATLAB software.The results of simulation show that the structure design of Urinary Minimally Invasive Surgery Robot are reasonable and it has large working space,and it meets the requirements of surgery.This robot has laid a certain theoretical foundation for the further research of this kind of robot.

Surgical robot; Structure design; Kinematics; Monte-carlo method

TP242

A

10.3969/j.issn.1003-6970.2018.10.009

西安市科技计划项目资助(2017074CG/RC037(XAGC006))

管声启(1971-)，男，西安工程大学教授，博士，研究方向为机器零件质量检测、机器人视觉等。

陈林梓，管声启. 泌尿微创手术机器人结构设计及其运动学分析[J]. 软件，2018，39（10）：42-47