基于ADAMS的多连杆高速压力机滑块运动特性曲线分析

袁丁益，鹿新建，陆文渊，袁 林，孙云飞，缪华滨

（南京工程学院 机械工程学院，江苏 南京 211167）

随着国内压力机械技术的迅猛发展以及精密引线框架等精密件的冲压技术需求，传统的曲柄连杆压力机已无法满足当前工业生产的需求。压力机正朝着高速度、高精度、驱动简单化方向发展。基于这样的发展背景，多连杆压力机在精密零件的冲压方面得到广泛应用。与传统曲柄连杆压力机相比，多连杆压力机具有下死点附近冲压速度低、加速度小的特点，并且具有明显的急回特性。这使得多连杆压力机有着较高的冲压效率，减小了冲压时产品的振动，提高了下死点精度。

本文研究多连杆传动机构相比于传统的曲柄连杆传动机构所具有的优势，并结合软件对模型进行仿真。研究了不同曲柄长度对滑块位移、速度及加速度的影响，有助于多连杆压力机传动机构的设计。

1 模型的建立

1.1 多连杆机构运动原理

图1为一种多连杆机构的运动简图。该机构左右对称，D和D′为肘杆CD、C′D′与机架的铰接点，H和H′为三角板FHC和F′H′C′与机架的铰接点。OA为曲柄，绕O点作圆周运动，通过连杆AB将运动传递到滑块上的B点，B点所在的滑块沿垂直方向做上下往复运动，带动摆杆BC（BC′）绕B点摆动，与此同时，肘杆 CD（C′D′）绕 D（D′）点摆动，通过连杆 CE（C′E′）将运动传递到滑块上的 E（E′）点，滑块受滑道约束在水平方向往复运动，并且通过连杆EF（E′F′）将运动传给三角板 FHC（F′H′C′），使得三角板绕着 H（H′） 点摆动。连杆 GI（G′I′） 一端与三角板 FHG（F′H′G′）上的 G（G′）点相连，一端和连杆 IJ（I′J′）上的I（I′）点相连，将三角板的运动传递给连杆IJ（I′J′），连杆 IJ（I′J′）受到连杆 II′和滑块 JJ′的约束，只能在竖直方向上下往复运动，并将运动传递给滑块JJ′。滑块JJ′在滑道的约束下，实现上下往复运动。

图1 多连杆机构运动简图

1.2 MBS模型建立

MBS模型主要由刚体、约束及驱动组成。由于本文研究滑块的位移、速度和加速度，刚体的质量属性参数不影响仿真结果，故建模时只考虑各杆的几何特征，采取ADMAS的几何建模工具，选取图1中的O点作为坐标原点，X轴水平向右，Y轴竖直向上，建模过程中自动生成的质量属性参数不变；定义机架和刚体上各关键点（铰接点），输入各特征点坐标值；在各杆件之间、杆件和机架之间添加铰链约束，滑块与机架之间添加棱柱约束；在O点铰链约束处添加旋转驱动，转速为600次/min。所建立模型如图2所示，包括21个刚体、19个关键点（关键点的坐标值如表1所示）和一个驱动。

表1 多连杆机构杆件几何参数

图2 仿真模型

由于模型左右对称，为了建模的方便，故只建立了左半边的模型，并对模型进行了简化处理。

2 仿真结果及影响因素分析

2.1 仿真结果

曲柄旋转角速度取600次/min，对多连杆机构的运动特性进行了仿真，获取了滑块的位移曲线、速度曲线以及加速度曲线。为便于比较，构建了具有相同滑块位移、滑块行程，上死点位置相同的曲柄连杆机构仿真模型，获取了滑块位移、速度以及加速度曲线。仿真结果如图3～5所示。

以冲压1.2mm厚的零件为例，定量分析多连杆压力机与曲柄压力机冲压过程中的运动学特性。从图3中可以看出，曲柄连杆机构接触零件时对应的曲柄转角约为153°，工作角为27°，而多连杆机构接触零件时对应的曲柄转角约为131.4°，工作角为48.6°。可见，使用多连杆机构大幅度地增加了工作角，延长了冲压过程中的工作时间，有利于减小冲压过程中的冲击。

图4比较了两种机构的滑块速度曲线，在下死点附近的工作角度范围内，曲柄连杆机构的平均冲压速度为186.93mm/s，多连杆压力机的平均冲压速度为94.86mm/s，多连杆机构的冲压速度与曲柄连杆机构相比要小得多，意味着只要送料速度和精度能够保障，还可以进一步提高多连杆压力机的冲压速度，而不会超出材料的允许冲压速度。此外，下死点附近的速度降低有利于压印等精密加工。在离开材料的回程阶段，曲柄连杆机构的最大速度为719.11mm/s，多连杆机构的最大速度为987.22mm/s。因此，多连杆机构具有急回特性。

图3 滑块位移曲线比较

图4 滑块速度曲线比较

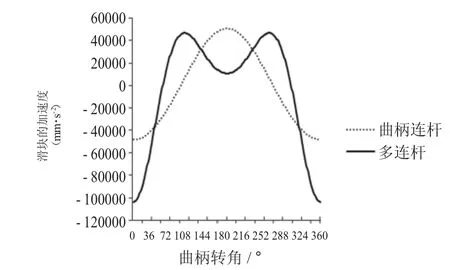
图5 滑块加速度曲线比较

图5比较了两种机构的滑块加速度曲线。曲柄连杆机构压力机的滑块加速度在工作角度范围内由44.99m·s-2逐渐增加到50.91m·s-2，在非工作角度范围内最大加速度为50.91m·s-2，基本上在一窄小高水平范围内变化。多连杆压力机的滑块加速度在工作角范围内由31.84m·s-2逐渐减小到10.69m·s-2，而在非工作角范围内达到-103.65m·s-2，在工作角范围较小的滑块加速度有助于消除滑块高速运动产生的惯性力对下死点精度的影响，减小冲压过程中产生的振动。

2.2 影响因素

在设计杆系结构的时候，可以将曲柄OA的长度设计成可以调节的，以此增强高速多连杆压力机的柔性。

如图6～图9所示为曲柄半径取20mm、25mm、30mm、35mm、40mm时，滑块的位移曲线、速度曲线、加速度曲线以及不同的曲柄半径对滑块行程的影响。

从图6中可以看出，随着曲柄半径的增加，滑块的行程不断增大，滑块位移曲线的底部逐渐隆起，这种曲线形态表明，滑块在下死点附近出现了波动。波动量过大不利于精密冲压，因此曲柄半径的增大会降低冲压精度。从图7可以看出滑块在下死点速度为零。随着曲柄半径的增大，滑块在下死点附近的速度减小，变化也更加平稳，更接近冲压工艺的需求。从图8可以看出，随着曲柄半径的增大，滑块在下死点附近的加速度减小，在非工作区域的加速度增大。

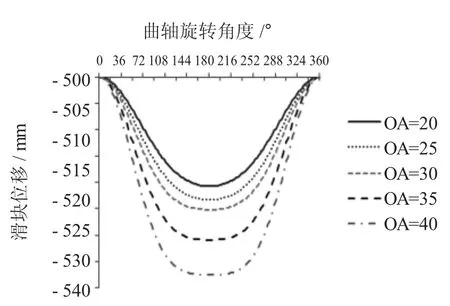
图6 不同曲柄半径时滑块的位移曲线

图7 不同曲柄半径时滑块的速度曲线

图8 不同曲柄半径时滑块的加速度

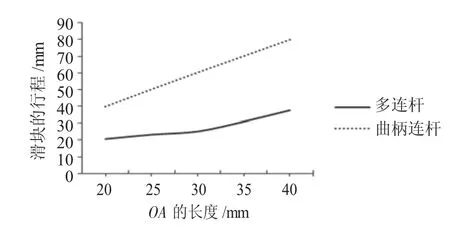
图9 不同曲柄半径时滑块的行程曲线

图9为滑块行程随曲柄半径变化的规律。从图中可以看出，随着曲柄半径的增大，曲柄连杆机构滑块的行程线性增加。而多连杆压力机构滑块的行程增加相对较小。因此，对于多连杆压力机而言，行程的增加不能单靠增加曲柄的半径，而且在结构上也存在一定难度。

3 结论

分析了多连杆压力机传动系统的运动过程，利用ADAMS软件建立了多连杆传动系统的多体运动学模型并进行了运动仿真，同时对影响滑块位移、速度及加速度曲线形态的因素进行了仿真分析，结果表明：

（1）与曲柄连杆机构相比，多连杆机构有利于提高冲压精度和冲压速度。

（2）随着曲柄半径的增大，滑块行程逐渐增大，滑块速度曲线及加速度曲线表现出相反的变化趋势。

（3）曲柄半径的增加引发滑块行程变化不显著。设计此类多连杆高速精密压力机时，应综合考虑上述因素的影响，以便获得最佳的结构参数。