一种半径测量仪及其测量方法
曾宪荣 吴晖辉 伍建桦
(顺德职业技术学院,佛山 528333)
1 研究背景
在生产实践中,经常需要对零部件内、外圆弧尺寸进行测量,目前普遍采用半径规、多功能游标卡尺、三坐标测量仪等专用工具。实践证明,此类专用工具都具有一定的局限性。
第一,半径规通常是用于测量半径为整数的小圆弧,大多数产品测量范围为R1~R25,测量精度低;第二,多功能游标卡尺适用于测量直径,对于轮廓为劣弧的半径分量则无法完成;第三,三坐标测量仪等高精度测量仪器,无法在生产现场操作,且操作耗时长、成本高。
在进行大量检索后发现,申请号为92205678.1、201620450144.1、200710190665.3的中国专利公开的仪器装置,均采用“弦高法”原理测量圆弧半径,即规定一段圆弧的弦长不变,通过测量弦高,并计算得到圆弧的半径。上述检测仪装置在进行现场测量圆弧半径时,测量结果不准确主要来源于四个方面:弦长不准确、弦高不准确、随机因素影响、多次测量时读数不重复。
故上述检测仪存在以下缺陷:刀刃形弦长测脚容易磨损,直接影响弦长的精度;测量弦高的测头轴线应在弦长的中垂线上,但固定式结构和刀刃式测脚均难以调整,定位准确度不高,不利于精密调整和快速校准;均采用百分表读数,使用者持仪器装置不稳,造成读数频繁跳动,难以确定测量值;测量数据均要代入公式进行复杂计算,使用不方便;固定式球形测头刀刃形测脚存在磨损,且无法更换。
2 半径测量仪结构设计
为克服现有半径测量仪器的缺陷,提供一种测量方法合理、误差小的半径测量仪本,现对半径测量仪结构重新进行设计,其结构如图1所示。
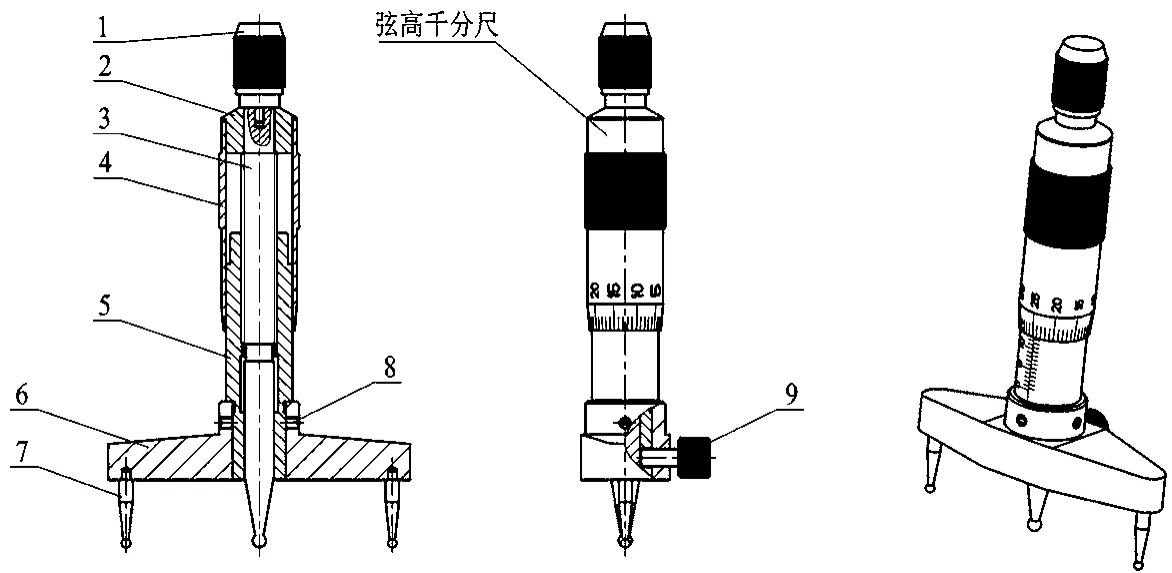
图1 半径测量仪结构示意图
本设计所提供的一种半径测量仪,包括挡帽1、接头2、测微螺杆3、微分筒4、螺纹套筒5、固定支架6、固定测杆7、调整螺钉8、锁紧螺钉9等零部件。所述挡帽、接头、测微螺杆、微分筒、螺纹套筒等零件,组成弦高千分尺。所述挡帽外圆柱面有滚花纹路,一端带有螺柱结构;测微螺杆一端为细牙螺杆,末端有螺孔,另一端为球状测头;微分筒为圆筒状,外圆周上有副尺刻度;螺纹套筒为空心轴,外圆柱面上沿轴线方向有主尺刻度。所述弦高千分尺,垂直安装在固定支架的中央,使用调整螺钉固定并调整;两个固定测杆垂直安装在固定支架两端的孔内;锁紧螺钉从侧面装入固定支架上,穿过螺纹套筒,可直接顶紧测微螺杆。通过四个方向的调整螺钉,可调整测微螺杆的轴线位置,使之处于两个固定测杆的中央。
3 半径测量仪工作原理
对圆弧的半径测量,尤其是非完整圆弧或大直径的零件,直接测量有困难时,可进行间接测量,常用方法是弧高弦长法,也就是测出圆弧的弦高h和弦长A,即可根据公式R=(A2/8h)+0.5h,算出圆弧半径。但该公式在测头为球形时,因实际测量距离和理论计算距离不一致,极容易造成误差而影响测量计算精度,而本设计的测头为球形,故不能直接使用此公式。
为解决此问题,重新建立数学模型,在本设计中,弦长A为定值,故只需测量弦高h,即可计算圆弧半径
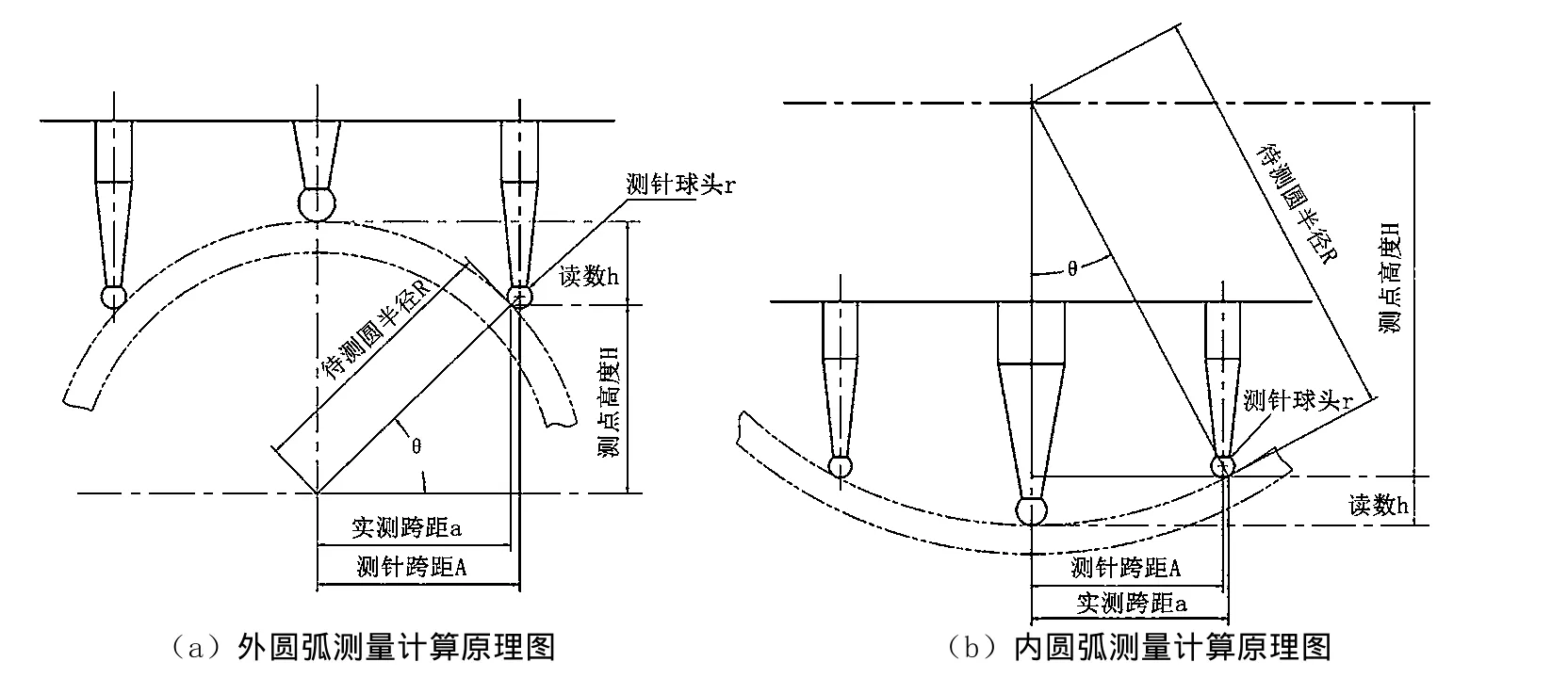
图2 外内圆弧测量计算原理图
3.1 外圆弧的测量计算
如图2(a)所示,设有∠θ、R、r、H、h、a、A。(球头半径r=2)
根据已知有:

根据各边的长度关系可知有:

将(1)(2)分别代入(3)(4)并整理可以得到:
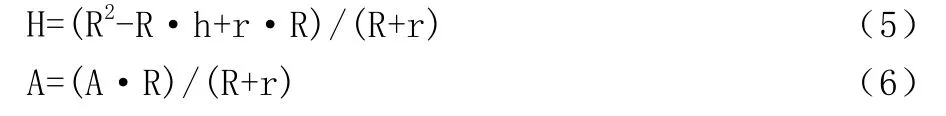
根据勾股定理有:

将(5)(6)代入(7)可得:
R2=[(R2-R·h+r·R)/(R+r)]2+[(A·R)/(R+r)]2
整理得:
R=(h2-2hr+A2)/(2·h)2
3.2 内圆弧的测量计算
如图2(b)所示,内圆弧半径计算的数学模型与外圆弧一致,故其计算公式与外圆弧计算公式相同。
4 误差分析
本设计在半径测量中误差主要集中在两方面:一是球头制造磨损引起的精度误差,导致弦长不是固定的理论值A;二是测量弦高的测头(测微螺杆)轴线应在弦长的中垂线上,实际由于制造误差,弦高测头轴线会偏离弦长中垂线。
4.1 球头误差分析
根据本设计的圆弧计算公式可知,球头误差在±0.1mm范围之内,对计算结果影响不大,R计算误差远小于0.1mm,对于受客观因素影响较大的机械量具而言,精度在可以接受的范围内。且本设计中固定测杆为可拆卸更换的,在使用一段时间,检测磨损较大球头半r误差较大时,作更换处理即可。
4.2 弦高测头轴线误差分析
由于测微螺杆与支架的配合有误差,使测头轴线不在固定测杆弦长的中垂线上,造成读数h有误差,进而使推算出来的圆半径R存在误差,如图3所示,分别采用固定测杆的可测量半径范围:(R20~R50),(R45~R200),(R180~R800),假定测微螺杆偏离中垂线值为ψ,通过列表计算可知高度偏差h1随测量半径增大而减小,而半径的测量误差随半径增大而增大。因此,取最大测量半径(R50,R200,R800)做极限计算。
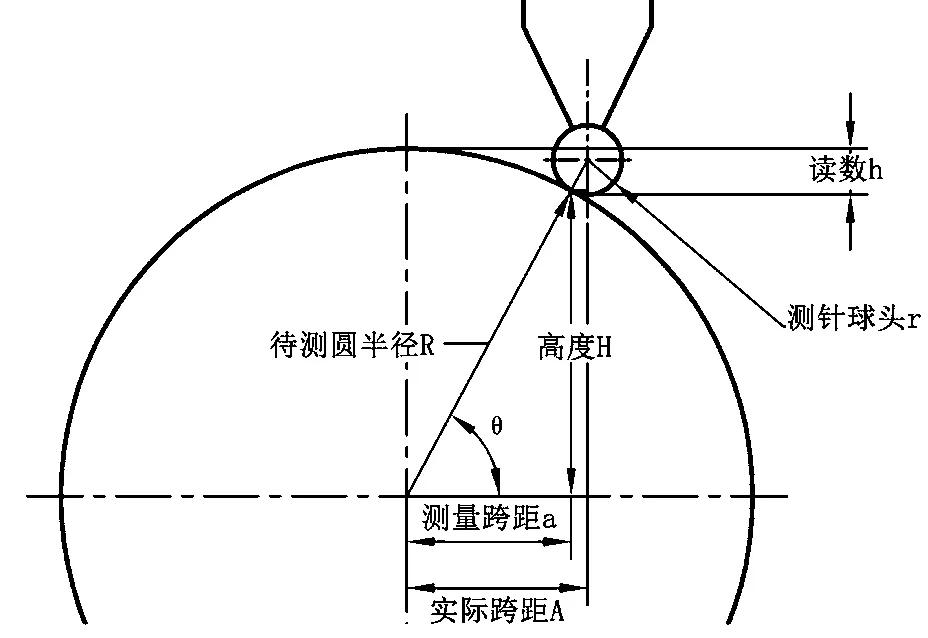
图3 测头轴线误差计算原理图
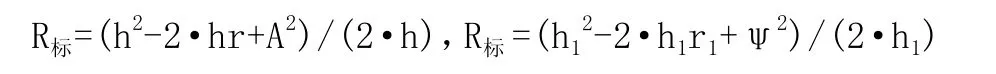
设有 R标、R误、h1、ψ(r=2、r1=3.8)
反求得:
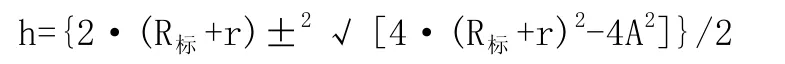
根据实际情况可得:
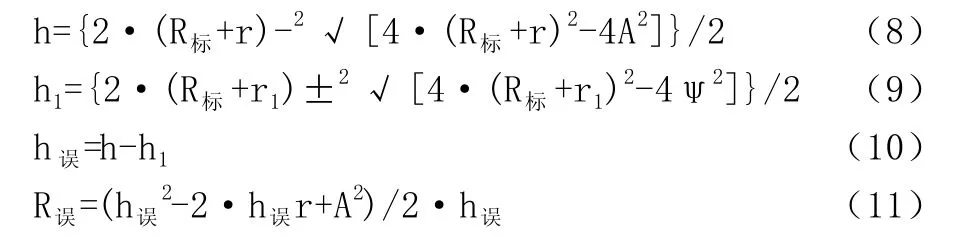
根据极限计算结果可知,当微螺杆偏离中垂线值为ψ为0.8mm以下时,半径测量误差小于0.5mm;当微螺杆偏离中垂线值为ψ为0.1mm以下时,半径测量误差小于0.05mm。实际上,根据现有加工条件,制造误差控制在0.1mm范围之内是完全可以实现的,且本设计本身就具备中心调整功能,在校正测量时可调整紧定螺钉来实现。
综上所述,固定测杆球头误差和微螺杆偏离中垂线重叠在0.2mm的范围内时,搬经测量仪的测量精度仍然符合大部分的测量场合要求,误差合理。
5 半径测量仪的使用与调整
5.1 半径测量仪的使用
为方便使用者快速测量工件的半径,本设计附带“弦高半径对照表”。使用者可在使用测量仪量取弦高数值后,直接在表中查出对应的圆弧半径值。此表精确到个位数,适合精度要求不高的场合。如需进行高精度测量,可代入半径计算公式中精确计算获取。
由于弦长A值固定,弦高h在半径值超过一定范围后,变化范围变小,故单一的弦长A固定支架不能满足实际需求,且极容易造成测量误差。为解决此问题,本设计根据弦高h的变化规律,取其变化较大,不易造成误差的范围设计了3种不同弦长的固定支架,以适用不同的测量范围要求,在使用过程中,可根据测量半径不同,选取更换不同弦长的固定支架即可。
5.2 半径测量仪的调整校正
在更换固定支架或使用一段时间后,需对半径测量以进行精度校正。首先,检测固定测杆球头的直径是否符合精度要求;其次,使用标准半径量块作为测量基准,通过调整螺钉,调整微螺杆偏离值,使半径测量仪的度数与对照表中度数一致,则调整校正完毕。
6 结语
分析几种测量圆弧半径的测量方法,并对现有测量仪器进行分析对比,找出存在的技术缺陷,设计了一种半径测量仪及其测量方法。该方法操作简单,测量后对照表格可直接获取所测半径值,同时具有测量精度高、测量结果、调整校正方便等特点,适合大部分一般测量要求精度的场合,但在高精度测量场合,仍需结合公式再进行计算。

