极值分布模型在动车组空调机组可靠性分析中的应用研究*
钱小磊
(北京纵横机电技术开发公司,北京 100081)
极值分布模型是可靠性建模中常用的一种,模型具有参数少、实用性强的特点。以实际运行动车组空调机组的故障数据为对象,研究了极值分布函数在动车组空调机组可靠性建模中的应用,重点研究了参数估计和分布拟合检验的方法及应用,期望为其他动车组产品的可靠性建模提供借鉴和参考。
1 动车组空调机组故障数据处理
可靠性试验一般的做法是从总体中随机抽取n个样品,在规定的工作条件下将其全部试验至发生故障并记录其观测值,得到样本故障数据。与常规可靠性试验不同的是,动车组每台空调机组装车上线运行的时刻不完全相同,即各个样品开始试验的时间起点不完全相同。为研究动车组空调机组的可靠性或故障规律,可引进空调机组发生故障时的运行里程T作为随机变量,将所有空调样品的试验“拉回”里程零点(即从里程t=0起计)统计各个空调的故障里程,如图1所示。
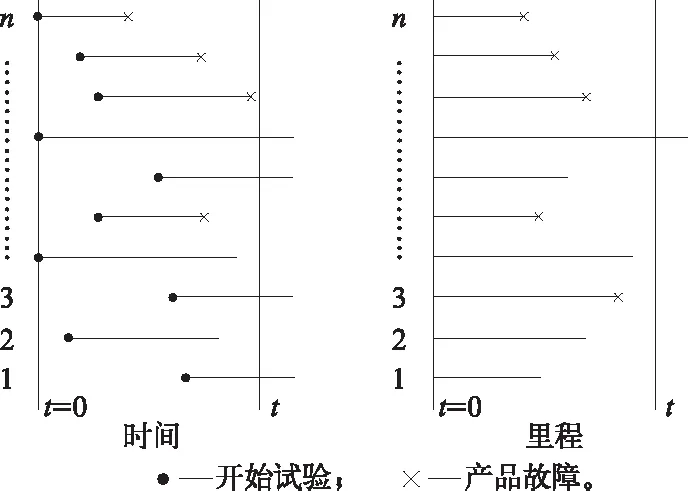
图1 空调机组可靠性试验数据
根据现行动车组检修规程,空调机组五级修(运行480万km或12 年)时其主要部件如压缩机、换热器、风机等需要更新,修复程度接近再制造,因此可将空调机组的可靠性试验看作试验终止里程为480万km的定时截尾试验。将试验终止里程均分成k个里程区间 ,统计每个区间的故障(须为首次故障)空调台数 和该区间内的空调机组总台数 (与固定样本容量不同,每个区间的样本数量为实际已运行至该区间下限里程的空调机组数量,因此各区间的样本数不完全相同,数据具有变样本容量的特点),则故障频率为:
(1)
累积故障频率为:
(2)
2 极值分布可靠性建模基本原理
2.1 模型介绍
极值分布概率密度函数:
f(t)=λexp[-λ(t-μ)-e-λ(t-μ)]
(3)
分布函数:
F(t)=exp[-e-λ(t-μ)]
(4)
2.2 参数估计
参数估计的常用方法有矩估计、极大似然估计、最小二乘估计等,考虑极值分布函数表达式可经变量变换转化为线性形式,采用最小二乘估计法。F(t)两边取对数有:
ln[-lnF(t)]=-λt+λμ
(5)
令yi=ln[-lnF(ti)],a=λμ,b=-λ,则分布函数变为:
yi=a+bxi
(6)
(7)
(8)
则参数估计值:
(9)
2.3 拟合检验
(1)χ2拟合检验
设总体X的分布函数为F(x;θ1,…,θl),θ=(θ1,…,θl)是未知参数,检验假设:
H0为总体X的分布函数为F(x;θ1,…,θl)
H1为总体X的分布函数不是F(x;θ1,…,θl)
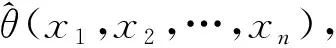
(10)
对于给定的显著性水平α,拒绝域为:
(11)
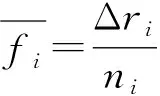
(2)线性回归假设检验
极值分布模型经变量变换可转化为线性回归模型,因此也可运用回归分析的假设检验方法,文中采用t检验法。
设线性回归模型:
Y=a+bx+ε,ε~N(0,σ2)
(12)
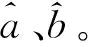
H0:b= 0
H1:b≠ 0
经证明,当H0为真时b=0,此时
(13)
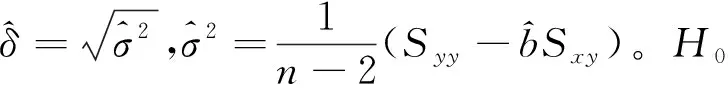
(14)
当假设H0被拒绝时,认为回归效果是显著的;反之则认为回归效果不显著。
3 实例分析
以某型动车组客室空调机组为例,将该型空调的0~480万km总运行里程划分为16个里程区间,统计每30万km区间内的样本空调数、首次故障空调数Δri,根据前文公式计算出故障频率、累积故障频率等可靠性指标,结果如表1所示。
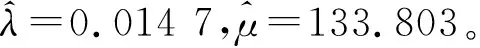
F(t)=exp[-e-0.014 7(t-133.803)]
(15)
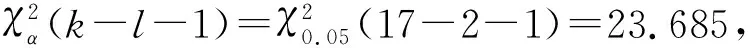

表1 某型客室空调机组可靠性指标计算细表
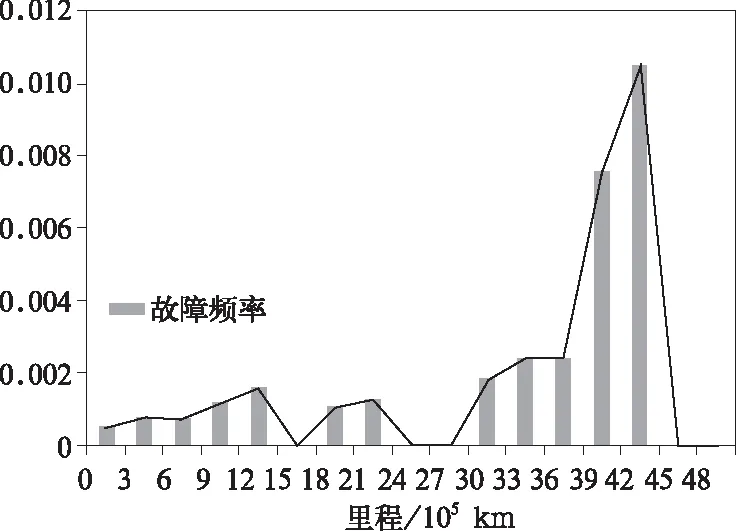
图2 某型客室空调机组故障频率直方图
因此认为线性回归的效果是显著的。该型客室空调机组故障概率分布拟合的效果可见图3。
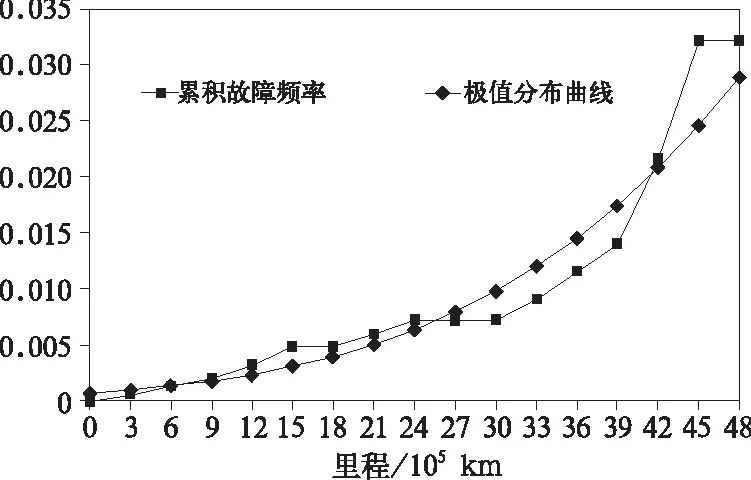
图3 某型客室空调机组故障 概率分布拟合效果
4 结束语
针对动车组空调机组现场故障数据具有变样本容量、截尾性质的特点,以极值分布模型的应用为例研究了可靠性建模过程。通过对常规可靠性指标计算和假设检验方法作适当变化和合理运用,参数估计和分布拟合检验均取得理想效果。实际算例表明,极值分布模型可较好反映某型动车组空调机组的可靠性特征,卡方拟合检验法可有效用于极值分布函数的假设检验。

