“三招”助力数学总复习教学

广西南宁市武鸣区马头镇马头小学玉元教学点(530100)

韦茂林

复习课上，如果教师只是抽取知识点，让学生被动识记的话，那这样的识记是模糊的，甚至可能是错漏百出的。学生不需要这样生硬的“钢结构”，而要具有生长力和智能型的“集成电路”。

一、查漏补缺，问题引导，搭建框架

复习不一定要放在学习所有的新知之后，而应趁热打铁，立即进行回忆、梳理，因为及时地查漏补缺不仅能为后面学生的分享交流提供依据，而且可以提高复习课的教学效率。

例如，复习“数的认识”之前，教师先让学生回顾所有学过的数集：(1)数的种类很多，有无数个；(2)数有正负数、奇偶数、合数与质数、分数、整数、小数之分；(3)正数前面可省去“+”号，负数一定要带“-”号；(4)质数除了1和它本身外没有其他的因数，合数反之；(5)偶数都可以被2整除，奇数则不行；(6)分数既可以表示具体数量，又可以表示比例；(7)小数和分数可以互化。这是学生自己的复习总结，都是提纲条文，从中可以发现学生脑海中的知识点是分散的，每个新知的出现没有建立在旧知的基础上，所以各知识点的层次、从属关系混乱。于是，教师以问题为导向，进行搭建框架的教学设计。

师：在复习“数的认识”之前，我们先梳理一下以下几个问题：我们学过的数有哪些？它们之间的关系是什么？如何分类？想办法把这些内容绘制成图谱。

(在学生思考回答后，师出示下表)

数的认识整数分数小数百分数奇数偶数素数合数真分数假分数带分数纯小数混小数不能被2整除能被2整除只有两个因数超过两个因数分母大于分子分母小于分子含有整数部分不含整数部分含有整数部分分母为100(%)的特殊分数

……

上表展现了知识间的内在联系，使学生真正理解和掌握各个知识点，为后期的交流探讨打下基础。

二、交流优化，深度梳理，内化吸收

复习课上，学生的交流分为两个层次：第一层次，教师引领学生构图，感受构建知识框架的优越性；第二层次，提炼方法，让学生体会到绘制知识图谱需要掌握全部的知识点。

例如，复习“数的认识”这一单元时，教师以数轴为主线贯穿教学始终：“请在数轴上表示出3、0.30、-3、6这几个数。”学生要在数轴上表示出这几个不同形态的数，首先要确定“1”的位置，也就是规划出单位“1”的长度。如对0.30的定位需要借助分数的意义，即将一个基本长度单位划分为10份，取其中的3份；对于3与-3的定位，则需要借助数轴的方向性与正负号的指代意义。同时，教师还可以指导学生总结经验，收集经典例题，使学生在命题、做题、评题的过程中学会从命题者的视角去理解和掌握所学知识。

三、意义迁移，整合统一，凸显思想

复习课上，教师在引导学生构建知识框架时，既要达到全面、深入、详细的要求，又要巧妙地整合提炼，做到厚积薄发。如对“能简便计算要用简便方法计算”这类题的复习，教师可先引导学生整理出所有的运算律，再寻找其中的相通之处，最后通过整合，使学生高效地掌握所学知识。

关于分配律，既可以是乘法对加数进行分配，又可以是乘法对被减数和减数进行分配，表达式为(a+b)×c=a×c+b×c、(a-b)×c=a×c-b×c，理解为“合并后再扩大相同倍数，可以先扩大相同倍数再合并”。细想减法的性质和除法的性质，表达式为a-b-c=a-(b+c)、a÷b÷c=a÷(b×c)，可以类似地解释为“分批分次减去(除去)两个数，可以集中一次性去除”，也可以看成为减法和除法的特殊结合律。

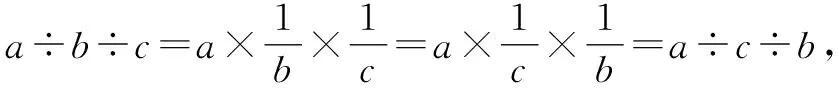
经过运算意义的贯通整合，各种纷杂的运算律就可以统一起来：在只含同一级的混合运算中，均存在交换结合定律；在含有两级的混合运算中都存在分配现象，即二级运算分配给一级运算。

总之，在将旧知梳理、融会贯通时，更需提炼出更为宏观的概念——数学思想、数学学习的策略方法，使学生能从更高的层面上掌握所学知识。