叶顶间隙几何不确定性对离心叶轮气动性能的影响

傅珏,蒋伟,柳一鸣,琚亚平,张楚华

(西安交通大学能源与动力工程学院,710049,西安)

受加工误差、服役环境等影响,离心叶轮叶顶间隙的几何尺寸呈现出一定的随机可变性,致使叶轮叶片上的载荷分布、边界层流态、分离流等与理想状态存在差异,导致叶轮实际运行性能偏离理想期望值,甚至急剧下降,对整机高效稳定和安全可靠运行构成严重威胁[1]。因此,精确量化叶顶间隙几何不确定性对离心叶轮气动性能和内部流场的影响具有重要的现实意义。

在叶顶间隙对离心叶轮气动性能的影响方面,芬兰拉普兰塔理工大学的Saaresti等对离心压缩机的叶顶间隙展开了数值模拟,结果表明,叶顶间隙对离心叶轮气动性能的影响呈线性关系[2]。赵会晶等以Krain叶轮为研究对象,研究了离心叶轮叶顶间隙泄漏涡的结构[3]。张楚华等通过研究叶顶间隙对离心叶轮气动性能的影响,发现随着叶顶间隙增大,离心叶轮气动效率、压比及转矩均降低,但变化曲线与线性函数相距甚远,呈现出典型的双平台变化关系[4]。刘正先等分析了典型叶轮相对叶顶间隙值在0～10%之间的叶轮气动性能、叶片载荷分布、间隙泄漏量的变化规律[5]。由以上研究可知,叶顶间隙对离心叶轮气动性能及内部流场的影响不容忽视,但这些工作主要集中于确定性流动分析,鲜有涉及离心叶轮叶顶间隙几何不确定性及其对叶轮气动性能的影响。

在离心叶轮气动性能不确定性分析方面,Javed等针对涡轮增压器用离心叶轮,采用蒙特卡洛(MC)取样方法[6],研究了叶片进出口叶顶间隙等一维设计参数几何不确定性对叶轮效率和压比的影响。Panizza等针对不同形式闭式离心叶轮,先后采用蒙特卡洛法、多项式混沌(PC)法研究了叶轮一维设计参数几何不确定性对叶轮乃至整级效率和做功能力的影响[7-9]。有必要对离心叶轮气动性能进行不确定性分析,研究对了解离心叶轮气动性能受几何不确定性因素影响下的统计变化规律具有指导意义,但缺乏对叶轮内部不确定性流动现象的研究,不利于深入认识几何不确定性因素对叶轮气动性能的影响机制。

因此,本文结合流体机械不确定性流动分析的学术前沿,针对考虑叶顶间隙几何不确定性的离心叶轮气动性能和内部流动展开了研究,从叶轮效率和压比性能曲线、叶轮出口流场、相对马赫数分布等方面进行探讨,为深入认识实际运行离心叶轮内部流场特征、提高叶轮性能对叶顶间隙几何不确定性的抗干扰能力、保证离心叶轮高效安全稳定运行提供了一定的理论参考。

1 非嵌入式多项式混沌法

1.1 方法概述

多项式混沌法作为一种不确定性量化方法,相较于基于蒙特卡洛取样的不确定性量化方法,能够在确保高精度的同时大幅度降低不确定性分析的计算成本[10]。按照与确定性求解器的耦合方式,PC法可分为嵌入式多项式混沌(IPC)法和非嵌入式多项式混沌(NIPC)法。其中,IPC法需要对求解器程序代码进行大量修改,存在一定风险和困难;NIPC法与之相反,仅将求解器视为一个“黑匣子”,在不确定性分析研究中的应用更为广泛。本文采用NIPC方法进行离心叶轮气动性能的不确定性分析,其基本原理概述如下。

假设U(θ)是概率空间(Θ,∑,P)上关于随机事件θ的随机过程,则U(θ)可表示成多项式混沌展式

(1)

式中:n为随机空间维数;p为多项式混沌展开式阶数;ψn(ξi1,ξi2,…,ξin)为关于随机变量ξ=(ξi1,ξi2,…,ξin)的正交多项式,其与概率密度函数ρ(ξ)相关。式(1)的简化形式为

(2)

利用NIPC方法求解不确定性分析问题的核心在于对多项式系数uk的求解。根据正交多项式的性质,可得

(3)

根据数值积分公式,有

(4)

式中:ξi、ωi分别为正交多项式ψk的零点以及相应的权重;m为积分点个数。

最后,计算U的均值和方差,即

E(U)=〈U(ξ)〉=〈ψ0U(ξ)〉=

(5)

(6)

1.2 方法验证

为验证NIPC方法在不确定性分析方面的有效性,分别以二维Sum Squares函数与三维Rosenbrock函数为例,将不同概率空间下预测所得输出响应的统计特征与基于MC方法所得统计结果(MC采样数为105)进行对比。二维Sum Squares函数与三维Rosenbrock函数的数学表达式为

(7)

(8)

假定ξ分别服从指数分布、高斯分布和均匀分布,对应的变化区间分别为[0,+∞)、(-∞,+∞)和[-1,+1]。采用NIPC方法生成关于ξ的4阶5点多项式混沌展式。在指数分布、高斯分布和均匀分布情况下,构造多项式混沌展式所需的正交多项式分别为Laguerre多项式、Hermite多项式和Legendre多项式。表1、表2分别给出了上述测试函数预测所得输出响应的均值和标准差数值与基于MC方法所得统计结果的比较,相应的概率密度分布如图1、图2所示。由对比结果可知,预测结果与MC采样分析的统计结果相当吻合,说明NIPC方法在不确定性分析方面具有较高的精度。

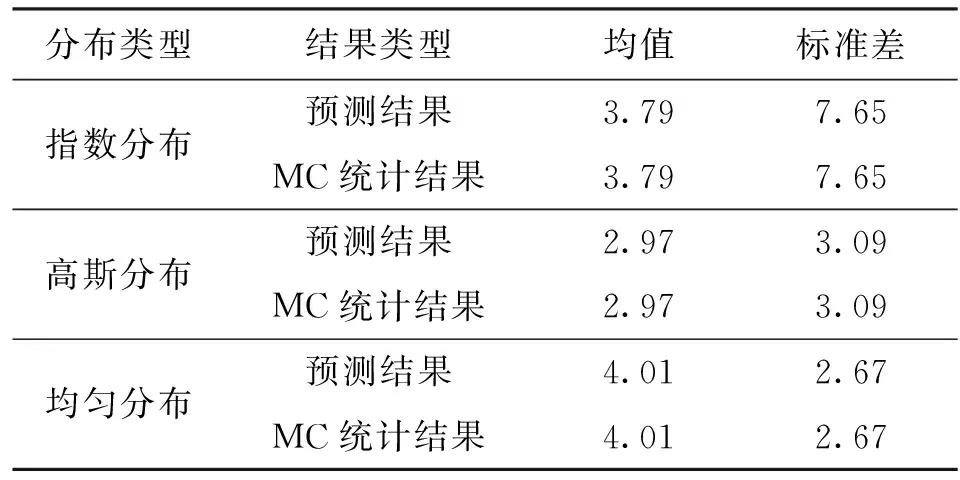
表1 二维Sum Square函数预测值与MC统计结果的比较

表2 三维Rosenbrock函数预测值与MC统计结果的比较

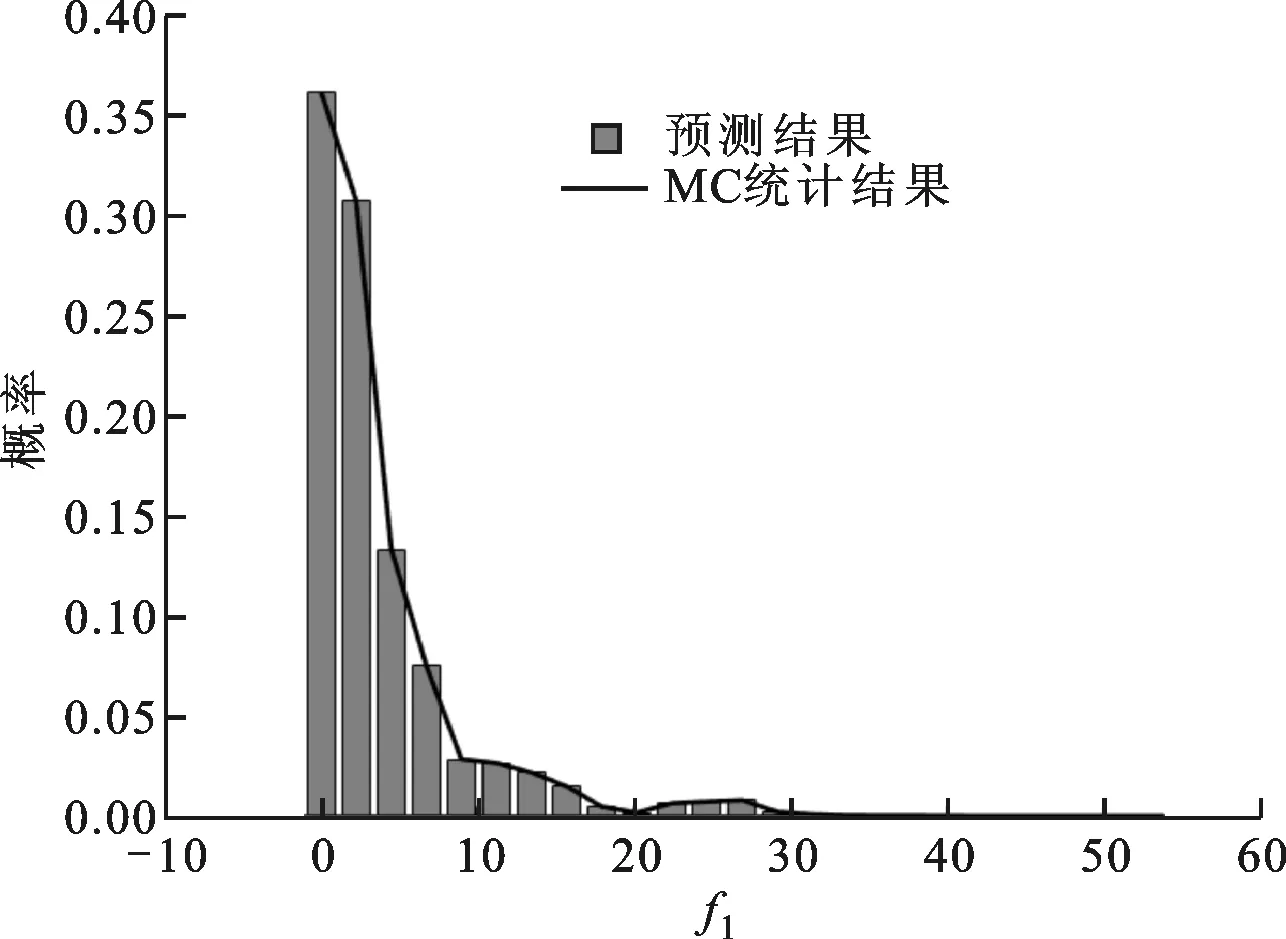
(a)指数分布

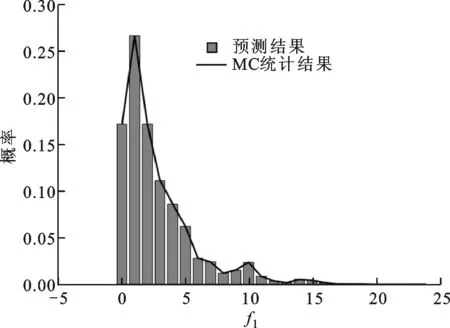
(b)高斯分布

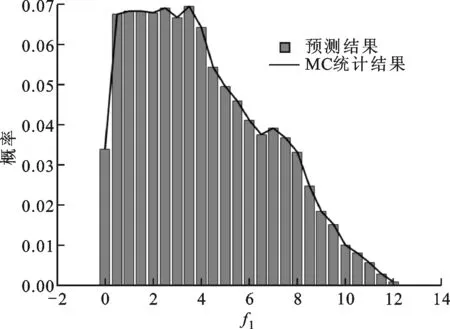
(c)均匀分布图1 二维Sum Squares函数预测值与统计结果对比图

(a)指数分布

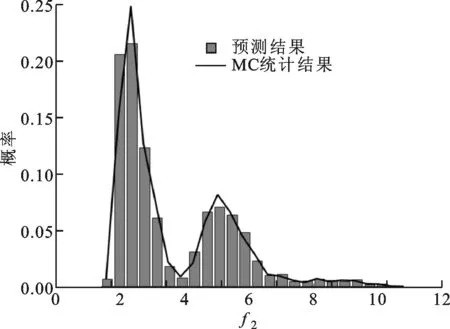
(b)高斯分布

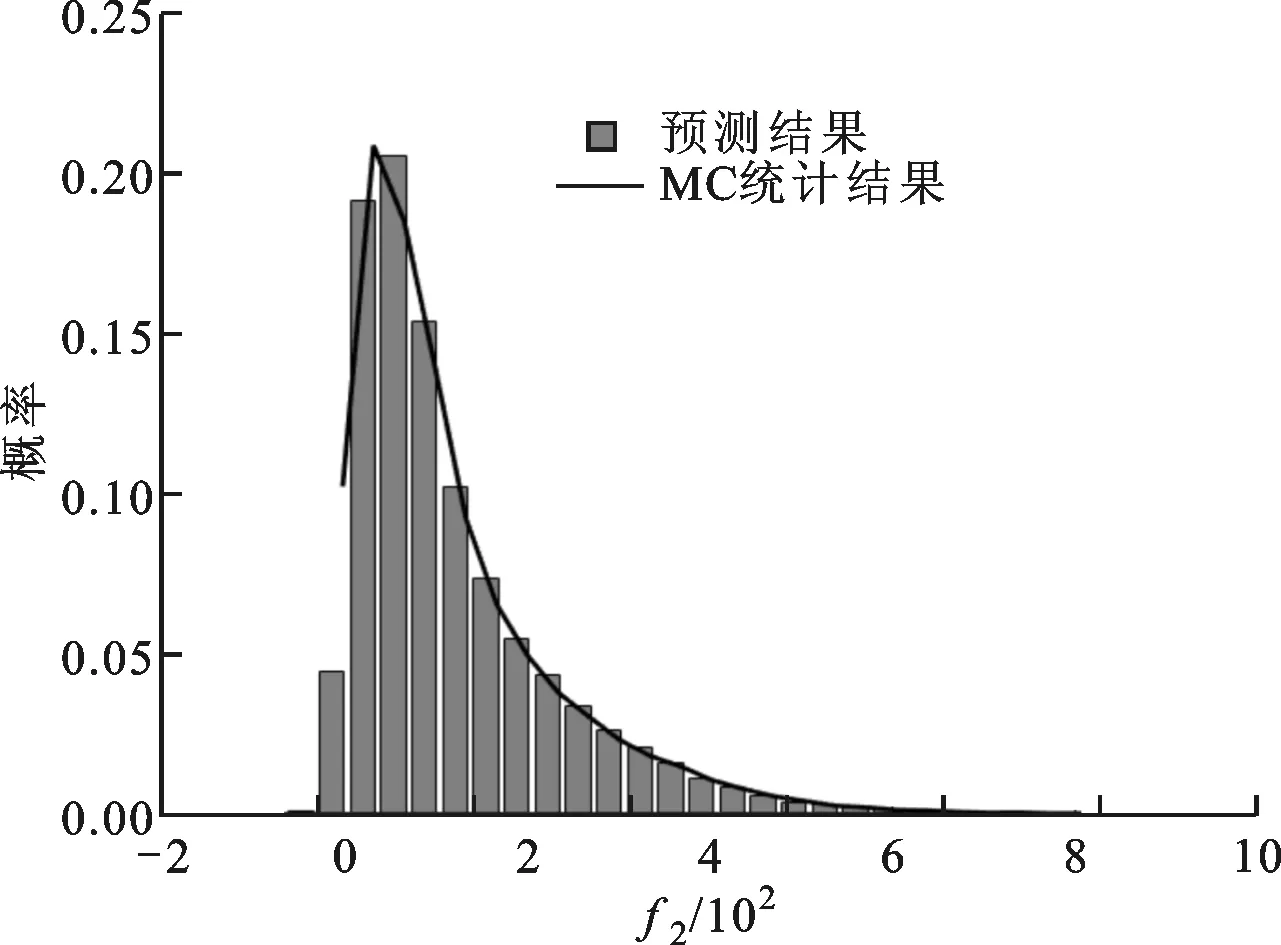
(c)均匀分布图2 三维Rosenbrock函数预测值与统计结果对比图

2 离心叶轮内流场数值计算方法

借助NUMECA Fine/Turbo软件,求解三维定常雷诺时均N-S方程,获得离心叶轮气动性能和内部流场。采用4阶Runge-Kutta法进行时间项离散,采用2阶中心格式并添加人工黏性的方法进行对流项离散,湍流模型采用S-A模型,并采用多重网格、当地时间步长和隐式残差光顺技术进行加速收敛。采用单通道计算模型,计算区域进口给定总温总压分布曲线和轴向进气,出口给定质量流量m,在周期性边界设定周期性边界条件,固壁为无滑移绝热边界条件。

本文研究对象为具有公开几何和实验数据的Krain离心叶轮[11],其前后缘叶顶间隙分别为0.5、0.3 mm,在Autogrid模块中生成叶轮单通道计算网格,如图3所示。为捕捉叶轮气动性能和内部流场受叶顶间隙几何不确定性影响下的变化情况,在叶顶间隙处沿叶高方向布置17个节点。通过网格无关性验证,当单通道网格总数约为630 000时,计算达到网格无关性要求,数值计算方法的精度验证可参考文献[12]。

图3 叶轮计算网格

图4、图5分别给出了计算所得叶轮子午面速度矢量图和叶轮出口1.05倍叶轮外径处周向平均速度沿叶高方向的分布图。由图4可知,在叶轮出口靠近轮盖侧存在明显流动分离,这与图5所示的局部速度波动相对应,故可采用速度波动峰值Vp的大小来定量反映叶轮出口流动的非均匀程度[12]。

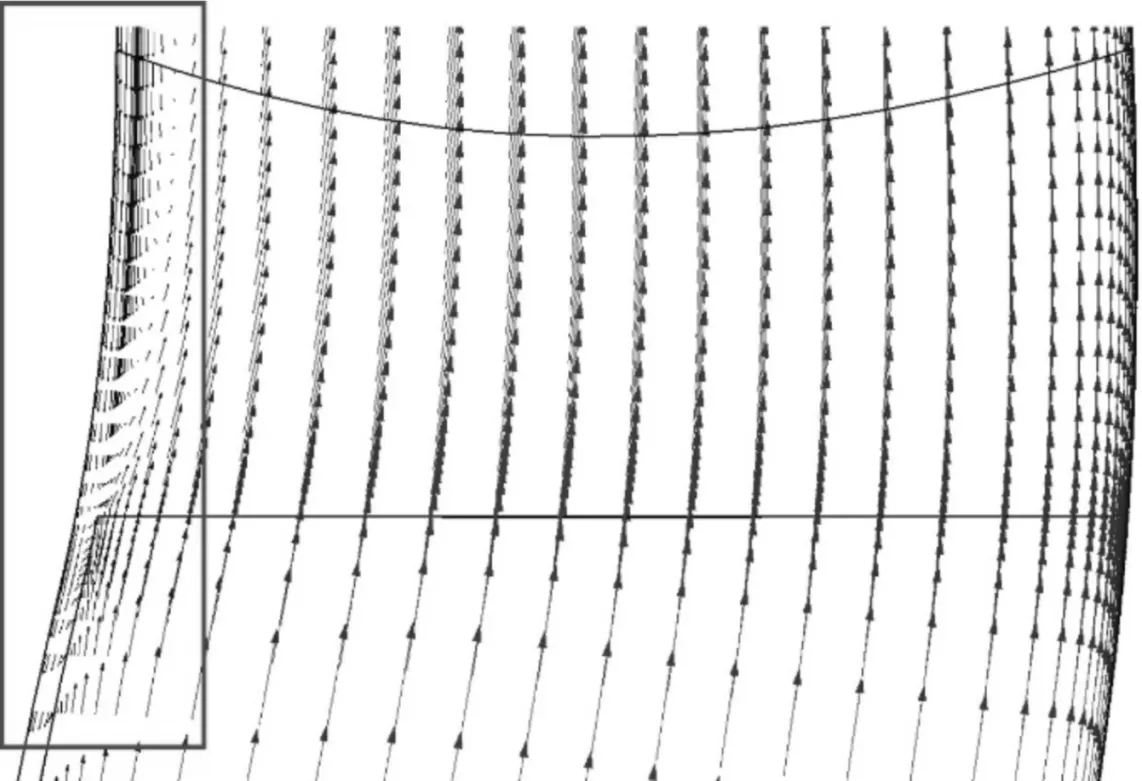
图4 叶轮子午面速度矢量

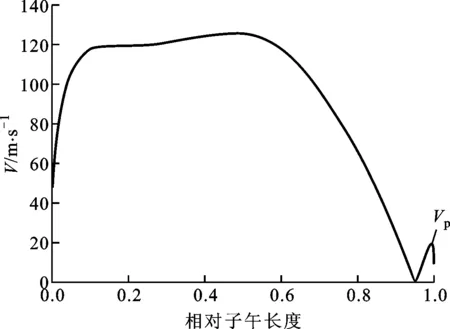
图5 叶轮出口附近周向平均速度沿叶高方向分布

3 离心叶轮不确定性流动分析

本节基于NIPC和CFD方法,研究了Krain离心叶轮叶顶间隙几何不确定性对叶轮气动性能和内部流场的影响。为简化分析,选取叶轮叶片进出口位置处的叶顶间隙为两个独立的几何不确定量,沿流动方向的叶顶间隙由进出口的叶顶间隙线性插值得到,由于流场计算为单通道计算,暂不考虑叶顶间隙沿圆周方向的不均匀性。考虑到叶轮叶顶间隙的真实分布规律难以准确测量,故选取自然界中普遍存在的高斯分布对叶轮叶片进出口位置处的叶顶间隙统计特征进行描述;同时,为保证叶顶间隙在合理的范围内波动,假定叶轮叶片进出口叶顶间隙大小均服从标准差为10%均值的高斯分布,即进口的叶顶间隙均值为0.5 mm、标准差为0.05 mm,出口的叶顶间隙均值为0.3 mm、标准差为0.03 mm。采用NIPC方法生成关于叶片进出口叶顶间隙的4阶5点多项式混沌展式,并针对7个流量工况点进行不确定性分析,共开展175次确定性CFD流场计算。

3.1 叶轮气动性能统计特征

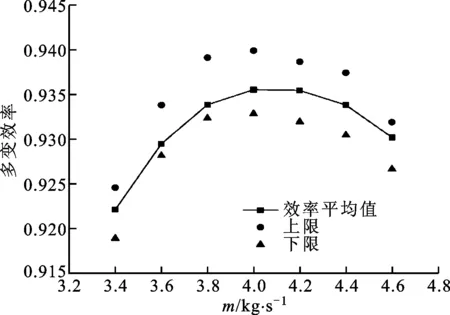
(a)多变效率

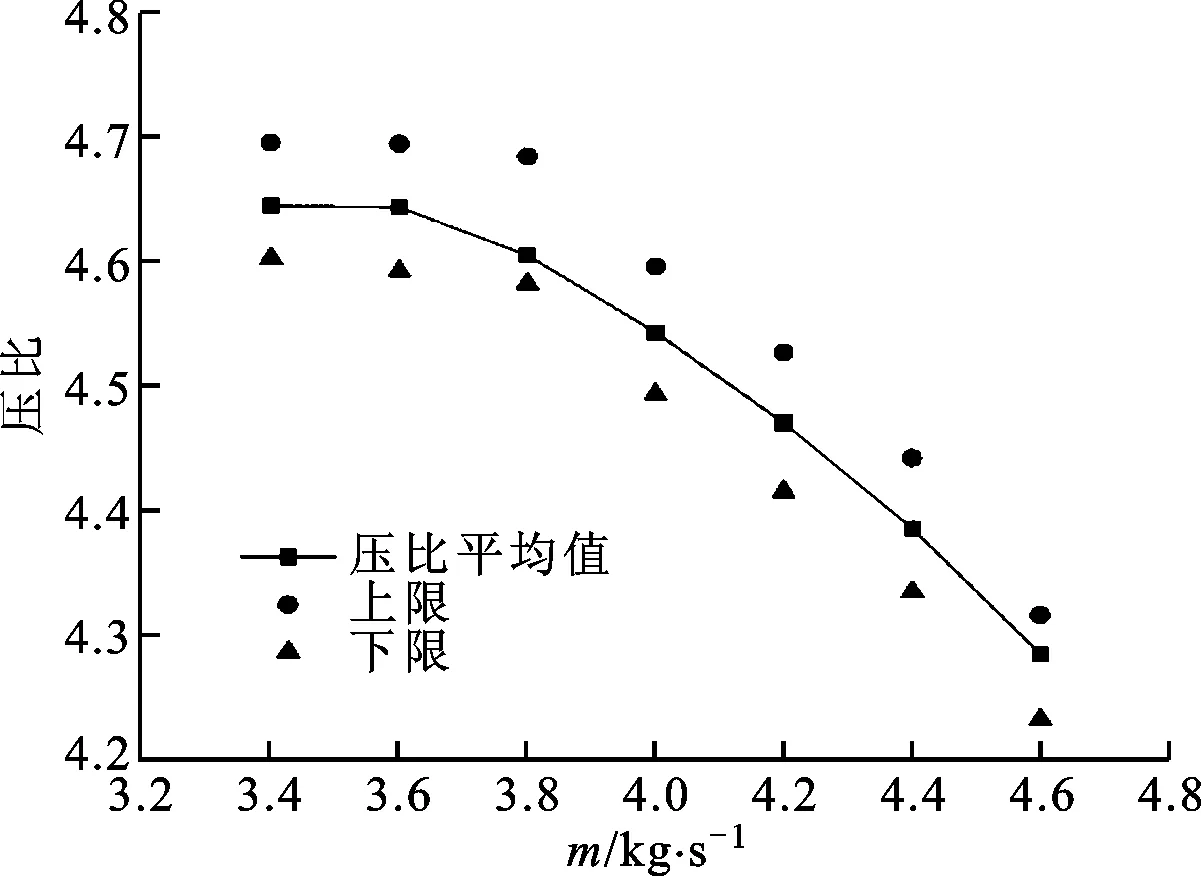
(b)压比图6 叶轮气动性能统计均值与不确定带分布

图6给出了预测所得叶轮多变效率和压比性能曲线的统计均值和不确定带,不确定带表示叶顶间隙在运行中的波动而导致的叶轮效率和总压比的变化范围。由图6可知,不同流量工况下,叶轮多变效率和总压比在叶顶间隙几何不确定性影响下的变化范围基本相当。

3.2 叶轮出口流动非均匀性统计特征

为探究叶顶间隙几何不确定性对叶轮出口流动均匀性的影响,给出了预测所得叶轮出口轮盖侧周向平均速度局部波动峰值Vp在不同流量工况下的统计特性,如图7所示。由图7可知,从近喘振工况到近堵塞工况,叶轮出口Vp均值及不确定带均随流量的增大逐渐减小,这说明随着流量的增加叶轮出口靠近轮盖侧的流动分离逐渐减小,分离流对叶顶间隙几何不确定性的敏感程度也逐渐降低。在近喘工况下,叶轮出口靠近轮盖侧的分离流最为明显,流动非均匀性最差,对叶顶间隙几何不确定性的敏感程度也最大。

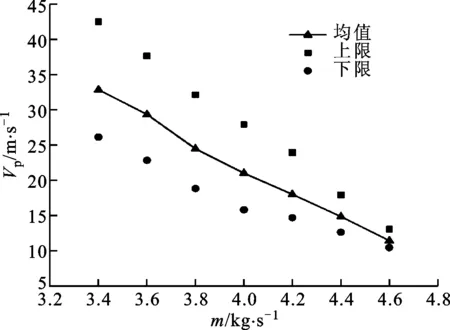
图7 不同工况下叶轮出口Vp均值与不确定带分布

3.3 相对马赫数分布统计特征

图8给出了预测所得设计工况下不同叶高截面处相对马赫数的标准差分布。由图8可知,在不同叶高截面,相对马赫数标准差较大的位置主要集中于流道后部且靠近压力面的地方,如图9所示。这主要是因为该区域相对流速较低,逆压梯度较大,流动较为不稳定,易受叶顶间隙几何不确定性的干扰。标准差极大值集中于叶轮叶片出口90%叶高截面区域附近,说明该处流动对叶顶间隙几何不确定性的敏感度最强,结合图4可知,该区域毗邻叶轮出口轮盖侧的流动分离区,流动稳定性较弱。此外,由图8c可知,尽管98%叶高截面更加靠近叶顶间隙区,且叶片出口位于轮盖侧的流动分离区内,但该处流场对叶顶间隙不确定性的敏感程度较90%叶高截面反而有所降低。这主要是因为98%叶高较90%叶高的气动载荷有所降低,流道内逆压梯度减小,未存在明显的低速区。

(a)50%叶高

(b)90%叶高

(c)98%叶高图8 设计工况下不同叶高相对马赫数标准差分布

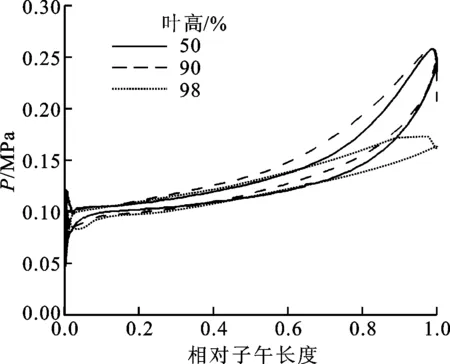
图9 设计工况下不同叶高处叶片载荷分布

考虑到90%叶高截面的流场最为敏感,图10进一步比较了另外两种典型工况下90%叶高截面的相对马赫数标准差分布。对照图8b可知,随着流量的增大,叶轮出口的标准差逐渐减小,说明叶轮出口流动对叶顶间隙几何不确定性的敏感程度逐渐降低,这和图7所示Vp的变化趋势相对应。然而,随着流量的增大,相对马赫数标准差极大值由叶轮叶片出口逐渐转移至叶轮前缘和靠近吸力面的区域。由此可知,叶轮进口及吸力面附近的流动对叶顶间隙几何不确定性的敏感程度随流量的增大而增大。对照图9、图11所示叶片表面载荷分布图可知,随着流量的增大,叶轮进口及吸力面附近逆压梯度变大,流动不稳定,易受叶顶间隙变化的影响。综上所述,随着流量的增大,叶轮出口流动对叶顶间隙的敏感性逐渐减小,而叶轮叶片进口及吸力面附近的流动对叶顶间隙的敏感性逐渐增大,二者相互抵消,这在一定程度上解释了图6所示叶轮效率和压比的不确定带变化范围在不同流量工况下基本不变的原因。

(a)近喘振工况m=3.4 kg/s

(b)近堵塞工况m=4.6 kg/s图10 近喘振与近堵塞工况下90%叶高处相对马赫数标准差分布

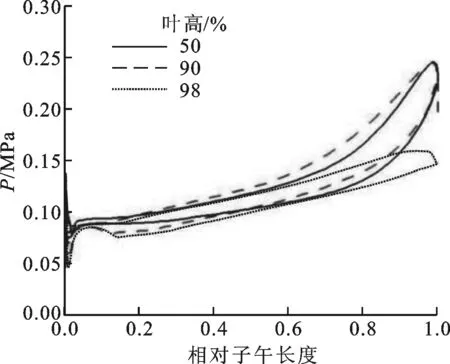
图11 近堵塞工况下不同叶高处叶片载荷分布

4 结 论

(1)非嵌入式多项式混沌法在随机变量服从不同概率分布的情况下,均具有良好的拟合精度,且相较于蒙特卡洛取样方法,计算效率显著提升;

(2)对于Krain离心叶轮,随着流量的增大,叶轮多变效率和总压比受叶顶间隙几何不确定性影响下的不确定带范围基本相当,而叶轮出口流动非均匀程度得到明显改善,且叶轮出口流动的非均匀性对叶顶间隙几何不确定性的敏感度也逐渐减小;

(3)Krain叶轮90%叶高截面区域对叶顶间隙几何不确定性的敏感度最强,且随着流量的增大,叶轮出口流动对叶顶间隙几何不确定性的敏感程度逐渐降低,但叶轮进口及吸力面附近流动对叶顶间隙几何不确定性的敏感程度反而逐渐增大。