单曲率特征自由曲面的相似性比较算法

王洪申, 汪雨蓉, 赵红红, 闫金堂

(兰州理工大学 机电工程学院, 甘肃 兰州 730050)

随着CAD/CAM技术的发展和在工程中的普及,三维CAD模型在设计和加工中的重用问题日显突出,三维模型的相似性评价是模型检索和重用的核心技术,受到广泛关注,学者们对三维CAD模型的相似性比较方法进行了较深入的研究,如Hilaga等[1]提出基于Reeb图的三维网格模型拓扑匹配方法;Bespalov等[2]对网格化处理的CAD模型进行形状检索,发现机械零件拓扑结构的微小变化会引起相似度的巨大差异;Bespalov等[3]提出基于尺度空间分解的层次特征分割方法,用于三维CAD模型的局部相似性比较。由于工程特性或美观的需要,自由曲面在工业产品中应用越来越多,自由曲面造型复杂、加工困难,重用自由曲面设计模型和数控加工规划具有更好的工程意义,这使得评价自由曲面相似性显得尤为迫切。You等[4]构建拓扑图,通过检测独立最大团方法,计算汽车覆盖件曲面模型的相似性;王洪申等[5]采用区域生长法对STL格式的自由曲面进行分割构建拓扑结构,利用赋权二分图最优匹配算法进行相似性比较;Fu等[6]研究鼠标、相机等自由曲面模型的相似性,提出基于高斯曲率积分的相似性比较方法;王洪申等[7]提出距离-曲率形状分布的方法,以距离-曲率矩阵的相似度得到曲面模型的相似性描述;张开兴等[8]从曲率云图中提取特征点的类Sift算子,通过比较局部特征的相似性实现2个曲面相似性的评价。Li等[9-10]运用层次分割图(HPG)表达注塑模具,并基于HPG图运用子图同构算法计算模具间的相似性。Huang等[11]提出一种以加工重用为目的的自由曲面相似性评价与检索方法。首先对曲面进行内容编码,初步过滤掉不匹配的对象,然后用D2算法[12]和子图同构算法评价自由曲面的相似性。已有研究都是通过设计抽象的几何描述子来表达自由曲面的几何特征,而在将自由曲面表达成几何描述子的过程中,不可避免地丢失了部分自由曲面的几何特征,从而限制了对曲面的几何形态描述能力。为了能以更细的粒度描述自由曲面的几何特征,又能满足检索对计算速度的需要,本文依据曲面曲率,提出适用于单曲率特征自由曲面相似性比较算法。该算法首先调整三维曲面的姿态,使相比较的曲面的Z轴方向一致,然后将待比较曲面做切片处理提取曲面上的截交线,以截交线上一系列点的曲率为依据判别相应曲线的相似性,将2个曲面的相似性度量转换为2簇平面曲线的相似性比较,以降维思想简化曲面相似性评价问题。

1 单曲率特征自由曲面的含义

曲面上点的曲率信息是曲面形状描述中极其重要的一个属性,能够可靠地反应曲面的形状特征。由微分几何知,曲面上某点处的2个主曲率为k1,k2,它们的乘积称为曲面该点处的高斯曲率,常以K表示,它们的平均数称为曲面该点的平均曲率,常以H表示。根据曲面上点的高斯曲率和平均曲率将自由曲面的特征定义为如下A,B,C 3类(如图1所示),本文研究的“单曲率特征的自由曲面”定义为:曲率特征单一,只有凸特征或凹特征或鞍型特征的简单自由曲面。

A类:K>0,H<0的曲面称为单一凸自由曲面,如图1a)所示;

B类:K>0,H>0的曲面称为单一凹自由曲面, 如图1b)所示;

C类:K≤0的曲面称为单一鞍型自由曲面,又叫双曲抛物面, 如图1c)所示。

本文约定:类型相同单特征自由曲面才有评价相似性意义,如果曲面类型不同则认为不具有相似性。

图1 单曲率特征的自由曲面分类

2 单曲率特征自由曲面的相似性比较算法

本文研究的是B样条表达的自由曲面的相似性评价算法,所设计算法的总体思路如图2所示,将一个自由曲面描述为一簇平面曲线的集合,2个自由曲面之间的相似性可以通过曲面上对应的2簇曲线的相似性来衡量。曲面上点的曲率信息能形象地描述曲面形状,本文设计的算法以点的曲率为核心参数,计算2个曲面上已提取的对应曲线的相似值,用所有相似值的平均值来评估2个单曲率特征自由曲面的相似性。

图2 本文算法思路

2.1 曲面做Z轴对齐处理

调整曲面模型在欧氏空间的摆放位置,将曲面的Z轴对齐。如图3a)所示,两凸曲面在空间的摆放位置不统一,2个面上各点法矢矢量和分别为N1,N2,由于曲面的位置不一致,可能无法得到正确相似性比较结果；通过对齐处理，如图3b)所示,使两曲面的法矢矢量之和的方向一致,均指向Z坐标轴的方向,即两曲面的Z轴对齐,此时曲面做截切处理,一一对应的截交线更能反映曲面的真实相似度,提高算法的精度。具体实现过程如下:

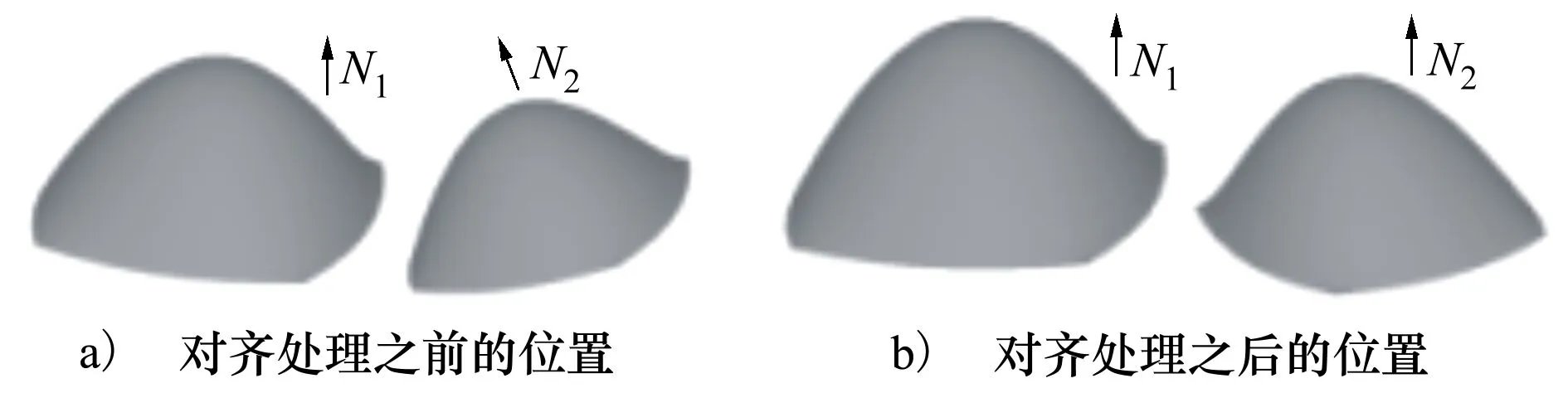
图3 凸面对齐处理

1) 设S={S1,S2}表示待比较相似性的同类单曲率特征的一个自由曲面集,首先依据曲面点的曲率值大小(不考虑正负号,只考虑数值的大小),分别在曲面S1和S2上遍历取点Pi(i=1,2,…,n)。曲率值大反映曲面的弯曲程度大,取分布较密集的点才能更准确地表达曲面的真实形状;曲率值小反映曲面的弯曲程度小,可以取分布较稀疏的点。遍历取点的步骤如下:

步骤2选定一个搜索起点P1(本文设起点为u=0,v=0处的点);

1) 依据前面所述,曲面上分布点的曲率较大时，所取的点比较密集，反之则所取的点比较稀疏,因此当k≠0时,设

(1)

式中，a1,a2,b1,b2是设定的计算参数，且a1≠0,a2≠0,b1≠0;

(2)

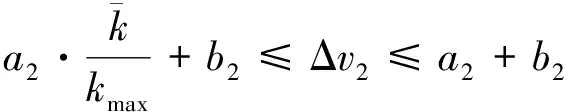
(3)

(4)

由公式(2)～(4)解得

(5)

公式(5)中,在给定范围内先确定参数a1,a2的取值,再由a1,a2确定参数b1,b2的取值。将a1,a2,b1,b2值带入到公式(1)中即可确定每次取点的Δv的值；

2) 当k=0时,取Δv=b1,此处b1与1)中的意义相同，且b1≠0;

步骤4固定起点的v参数,在参数曲线v=0上以同样方法计算参数距离Δu寻找下一个v参数线的起点,再重复步骤3，找到该v参数线上相应的曲面点;

步骤5重复步骤4,直到u参数线方向的数值越界，即可按曲率大小搜索到整个曲面上的点。

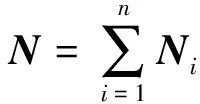
本文输入图4所示的凸曲面,计算公式(5),取a1=10-4,b1=0.03,a2=0.02,b2=0.002,4个参数值带入公式(1)找到曲面上的所有点(图4中的黑色十字交叉点)。

图4 凸曲面上取点

2.2 调整曲面大小

在工程中,有时讨论自由曲面的相似性并不考虑曲面的大小,为了消除曲面尺度对相似性评价的影响,此时需要对曲面进行比例缩放。曲面满足Z方向的对齐后,对其中一个单曲率特征的自由曲面(本文选曲面S2)做比例缩放变换以调整大小,使两曲面在Z坐标轴的方向具有相同的曲面高度,用相同数目的等距平面分别截切2个曲面,处理结果如图5所示(XOZ面内的实体投影图,其中黑色线条是截切处理后生成的截交线)。图5a)的2个凸特征自由曲面S1和S2的形状相似、大小差异明显,工程应用中需要考虑曲面大小尺度对相似性评价的影响时,曲面不缩放,直接对其进行截切处理,计算曲面的相似度量值(相似值为0.491),用于评价考虑曲面大小时的相似性;若将曲面缩放,消除两曲面的大小差异,如图5b)所示,使两曲面在Z方向具有相同的高度范围,相应的相似度量值为0.126,符合人的感官判断,这种情况适用于工程应用中不考虑曲面大小时的相似性评价。

图5 凸曲面的缩放变换

2.3 曲面做截切处理

三维自由曲面模型的表面形状较复杂,微小变化会引起曲面的不同,直接比较其相似性有一定的难度。而曲面做平面截切处理可将三维空间曲面形状的描述问题转换为二维平面曲线的形状描述问题,简化曲面相似性的比较。因此以降维的思想,用垂直于Z轴的相同数量(设为m)的等距平行平面T={Ti}(i=1,2,…,m)分别截切曲面S1和S2,在曲面S1和S2上生成各自的等高线,得到一一对应的平面曲线(如图5所示)。设M1,M2分别是曲面S1和S2上分布的截交线集合,则:

M1={Curvei|Curvei⊂S1}(i=1,2,…,m)

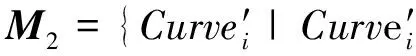
2.4 计算曲线的相似性

通过对曲面的截切处理,得到能反映单曲率自由曲面特性的一系列平面曲线,为了准确描述曲线特征、合理表征曲线的相似性,以曲率为变量,用两曲线曲率的Earth Mover′s Distance(EMD)值描述其相似性。EMD,也叫推土机距离,是一种距离度量的定义,能通过一次线性规划计算出2个大小不同(或相同)的几何或向量的距离。对于2条曲线,其形状大小越相近,EMD值越小,相似度越高;反之,则表示其差别越大;形状大小完全相同时,EMD恒为0。

1) 曲线相似性评价

(6)

公式(6)的Ei代表第i对曲线相似的度量值。

2) 曲线相似性算法验证

为了验证2条平面曲线的相似性评价算法,设定2组曲线:Ellip1、Ellip2、Ellip3和Curve1、Curve2、Curve3、Curve4,同组曲线中,第一组为椭圆曲线,第二组为B样条曲线(包括开曲线和闭合曲线),其中Curve1、Curve4是形状大小相同、位置不同的B样条闭合曲线,如图6～图9所示。

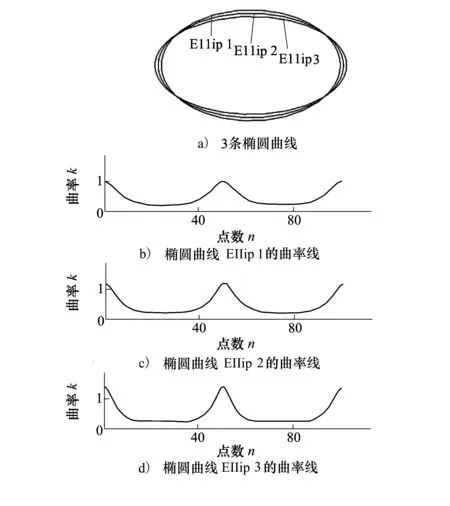
图6 3条椭圆曲线及其对应的曲率线

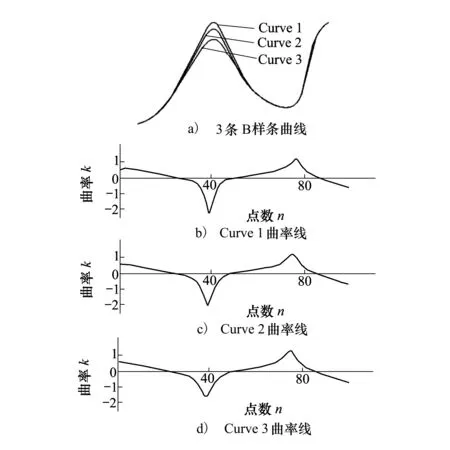
图7 3条相比较的B样条开曲线及其曲率线

图8 3条相比较的B样条闭曲线及其曲率线

图9 形状相同位置不同的B样条曲线及其曲率线

分别在每条曲线上沿曲线方向等弧长取相同数量(设为n)的点,并计算各点的曲率(相对曲率),作为EMD度量的参数,依次计算两两曲线的EMD值,为直观反映曲率大小的变化,在平面坐标系中绘制曲率分布线。由于不同曲线之间存在长度上的大小差异,因此需要对曲率分布线的尺度进行归一化,本文实例以曲线上等弧长的长度作为曲率线横坐标的间隔,其中横坐标代表所取点的数量(坐标原点是第一个点),纵坐标代表点的曲率值。

曲线的类型、相关数据及图形、对应的曲率线如图所示,图中取点数量n=100时曲线所对应的曲率线,曲线发生微小变化,则曲率线产生局部差异。计算同一曲线类型中两两对应曲线的EMD值度量其相似性,结果如表1所示。曲线图形是形状有微小差异的平面曲线,根据人的直观视觉判断,图6中椭圆曲线Ellip1、Ellip2的形状大小最相近,Ellip2、Ellip3次之,Ellip1、Ellip3的形状相差最大,计算结果，两两曲线的相似程度Eij满足关系:E12(Ellip1,Ellip2)>E23(Ellip2,Ellip3)>E13(Ellip1,Ellip3)，结论与人的感知相同。图7和图8中B样条曲线相似程度Eij也满足如上关系式，结论与人的感知相同。图9所示的闭合曲线，Curve1、Curve4的形状大小完全相同，但位置不同，评价的相似值恒为0，评价结果与实际相符，表明选用EMD距离描述平面曲线相似性时，无需考虑曲线在平面内的方位。表1数据显示：无论描述椭圆曲线还是B样条曲线，两两曲线的相似度量值随着形状差异的增大呈递增趋势，符合人的感官判断，满足各曲线间实际的相似关系，所以在应用中，EMD距离适用于平面曲线的相似性比较。

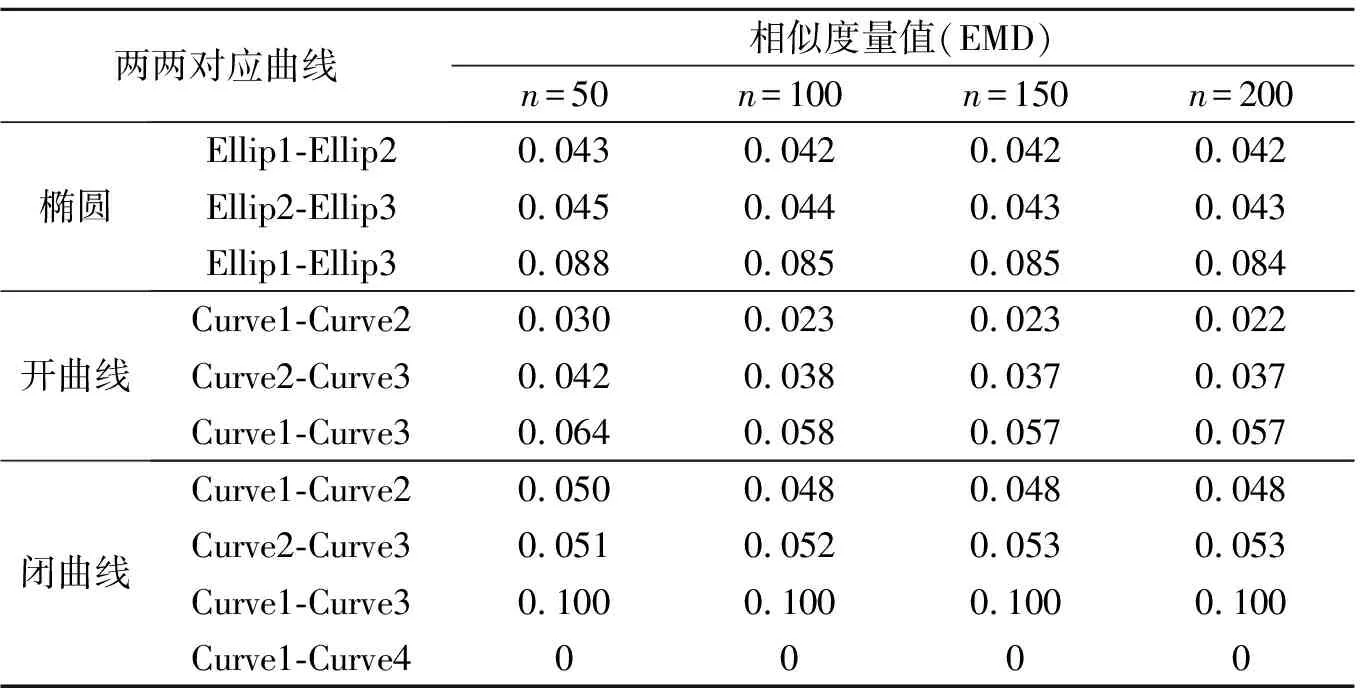
表1 曲线图形的EMD度量值的比较

2.5 计算曲面的相似度量值

三维曲面的表面形状映射为一组二维曲线,2个相比较的三维曲面的相似性度量转化为对应的2组平面曲线的相似性度量。用2.4节公式(6)计算对应曲线的相似值并求和即为两曲面的相似值。由于曲面做平面截切处理时,截切平面的数目变化会影响截交线相似性的总和,为了避免该问题,对曲线相似度量值的总和求平均值,以该平均值作为曲面的相似性评价指标,记作:

(7)

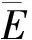
3 实验与讨论

基于OCC(Open CASCADE)开源3D建模库,以Microsoft Visual Studio 2010为集成开发环境,分别用第一节中定义的A,B,C 3类单曲率特征自由曲面验证本文相似性评价算法。主要验证以下属性:(1)自由曲面绕Z轴任意旋转对相似性评价结果的影响;(2)曲面的缩放操作对相似性评价结果的影响;(3)截交线的数量对相似性评价的影响。根据以上实验目的,对每类(A,B,C类)单曲率自由曲面构造2个B样条曲面,并分别设计3组实验,组号分别记为X-Ⅰ、X-Ⅱ、X-Ⅲ(X取A,B,C)。实验方法:X-Ⅰ组在曲面相似性比较中,不对曲面进行缩放操作,相比较的曲面位置是对齐的;X-Ⅱ组曲面不缩放,同时曲面S2绕Z坐标轴做旋转变换;X-Ⅲ组对曲面进行缩放。对每组实验分别用10种截切间距截切曲面,由公式(7)计算两曲面的相似度量值,在实验中,曲面的每条截交线上参与计算的点均取100个。

3.1 曲面的相似性评价实验数据

图10～图12为单曲率特征自由曲面的3种基本类型曲面实验图例,表2～表4是实验所得的数据。

图10 凸特征自由曲面的实验(A组实验表2) 图11 凹特征自由曲面的实验(B组实验表3) 图12 鞍型特征自由面的实验(C组实验表4)

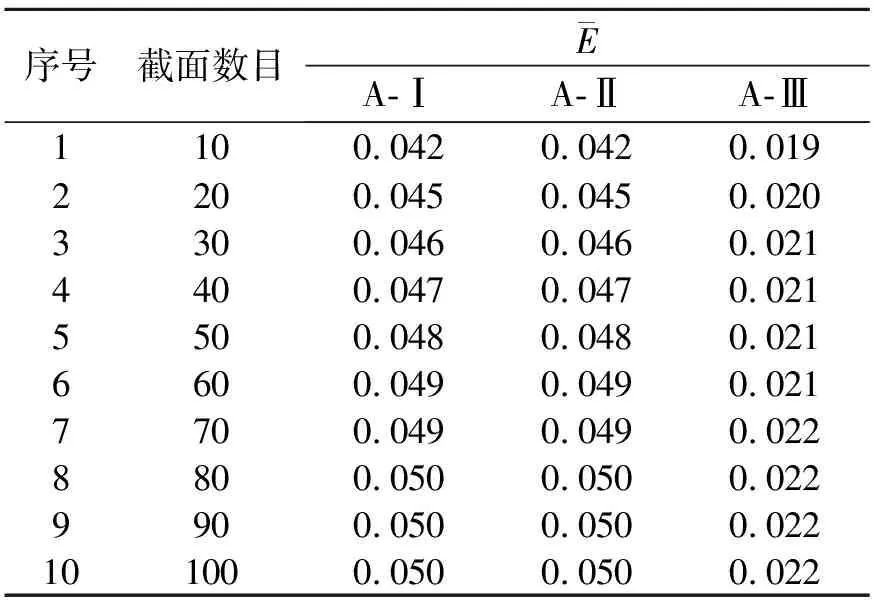
表2 凸特征自由曲面的相似性比较

图13 凸曲面不同截面数目的EMD分布线图

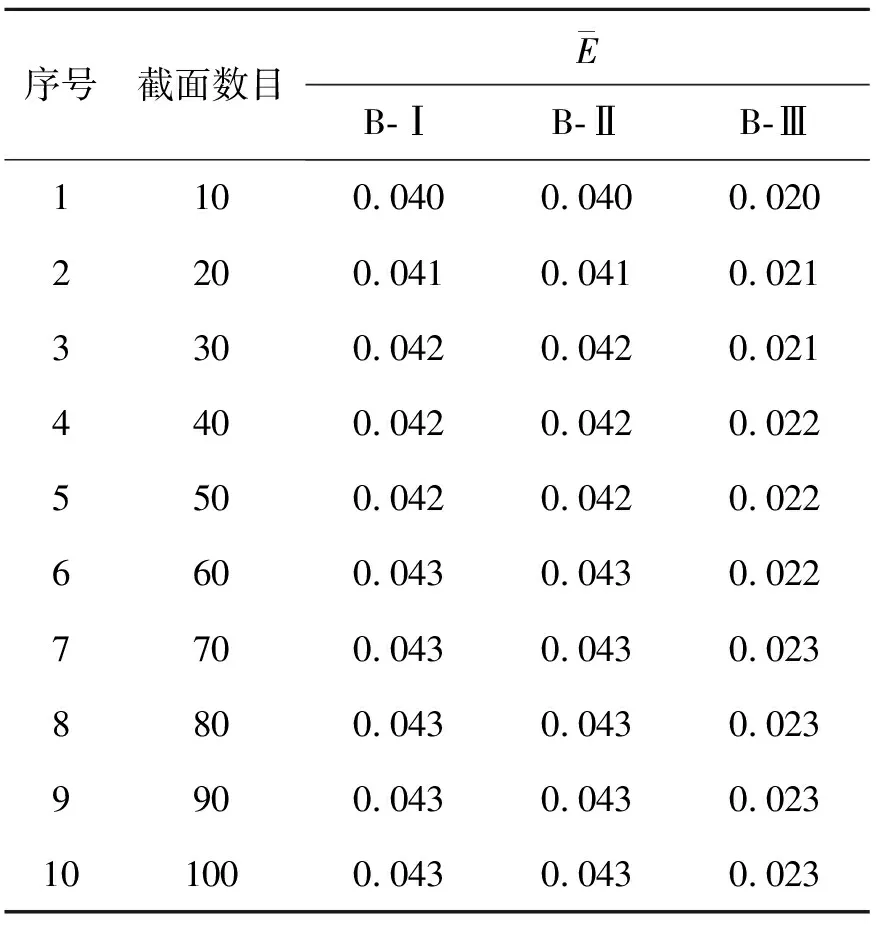
表3 凹特征自由曲面相似性比较

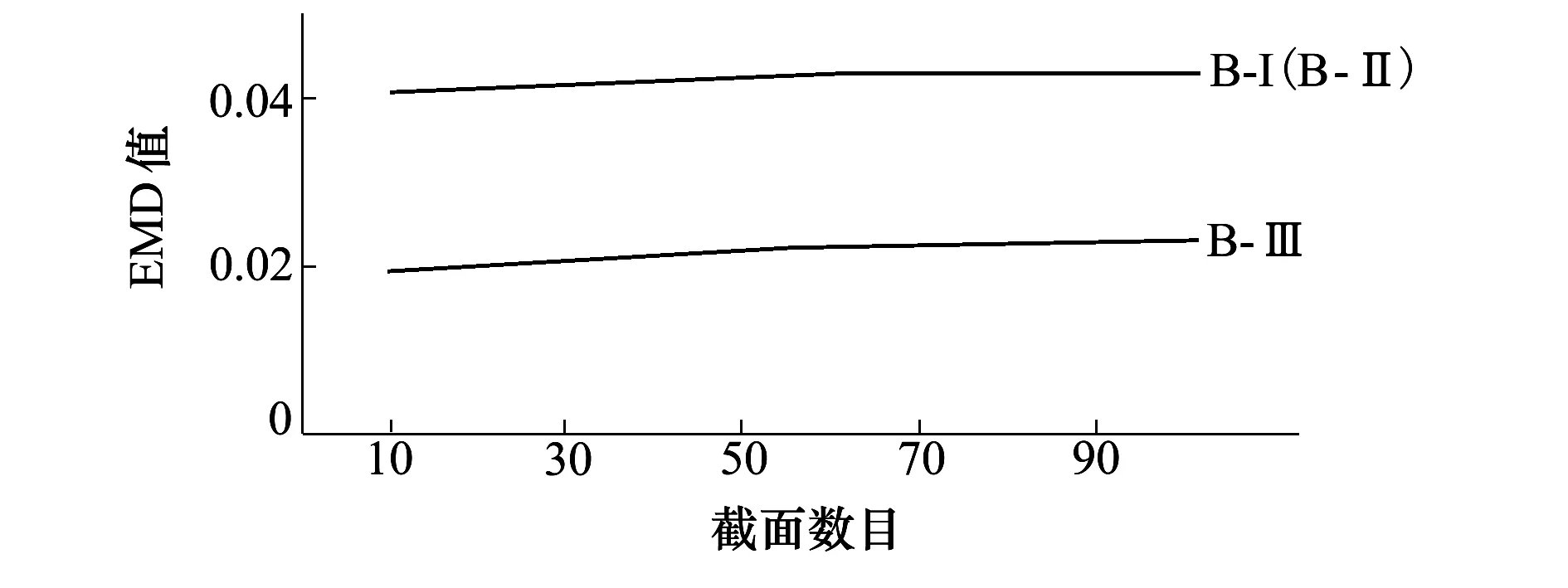
图14 凹曲面不同截面数目的EMD分布线图

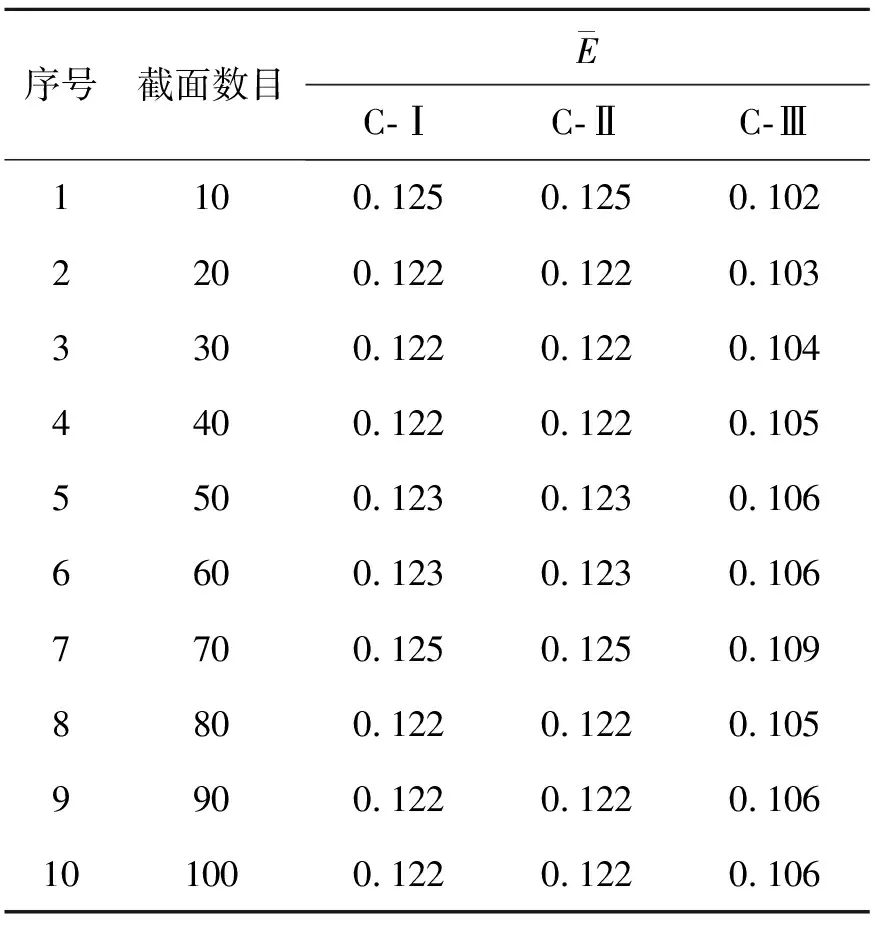
表4 型特征的自由曲面相似性比较

图15 鞍型面不同截面数目的EMD分布线图

3.2 相似性评价实验分析与讨论

4 结 论

曲率是曲面的重要微分几何特性,其大小与自由曲面模型在欧氏空间的摆放位置无关,本文利用曲率的这种属性设计了单曲率自由曲面相似性评价算法。首先运用降维思想,用垂直于Z轴的平面对单曲率特征的B样条曲面做截切处理,得到曲面与截面的交线信息,将三维空间模型转换为较简单的二维平面图形的集合,然后以EMD距离度量平面曲线的相似性,由此反映自由曲面的相似性,方法可靠,便于计算,对考虑曲面大小和不考虑曲面大小的情况都适用。通过大量的实验验证,设计的算法简单可行,并具有如下属性:(1)对相比较的2个自由曲面仅需对齐一个坐标轴;(2)算法既适用于考虑大小的曲面相似性评价,也适用于不考虑大小的曲面相似性评价;(3)相似性评价指标收敛。