基于OTSUKF的飞行器惯性测量单元的故障诊断

何启志, 章卫国, 黄得刚, 陈华坤, 刘璟龙

(1.西北工业大学 自动化学院, 陕西 西安 710129; 2.兵器工业集团 航空弹药研究院, 黑龙江 哈尔滨 150036)

惯性测量单元(IMU)故障已经成为当前军机、民机以及无人机飞行事故的一大主要原因。1995年，Dryden飞行研究中心对Perseus飞行事故进行分析，确定事故原因为：俯仰角速度传感器故障导致飞行速度超出正常范围限制，机翼承受过大气动力而发生折断。2005年，MH 124客机飞行过程中遭遇主飞行仪表数据显示矛盾、自动右转向、自动超高度飞行等一系列问题，飞行事故原因确定为大气数据惯性基准组件中的加速度传感器故障。

现阶段国内外飞行器主要基于硬件余度和表决检测来实现惯性测量单元的容错。惯性测量单元常见的余度配置方案包括正交配置和斜置配置2种，Honeywell公司的ARINC704惯性基准系统，采用正交配置和表决监测实现惯性测量单元的容错，波音公司的Boing-777采用斜置配置及广义似然比检验方法实现惯性测量单元的容错。硬件余度方案可以大幅度提升飞行器关键传感器的容错能力，但是也具有成本较高及容易发生共性故障的缺点。例如，虽然飞控系统关键传感器采用多余度配置，但是自2003年起，仅大气数据传感器故障引发的民机飞行事故多达35起。这些事故的典型的代表有2008年美国B-2轰炸机坠毁，2009年法航447航班事故都是由于飞控系统关键传感器共性故障引起的。共性故障导致飞行事故的原因是传感器硬件配置的相似余度，如果进行非相似余度配置，可以进一步提升飞行器的容错能力。解析余度的引入一直是飞行器传感器容错中的热点问题，它的引入可以补充硬件余度的不足。

解析余度技术依赖于飞行器的动力学和运动学模型，飞行器的动力学模型和运动学模型以微分方程表达，通过对状态微分方程的积分可以得到传感器容错所需要的状态信息。但是传感器的噪声及故障是广泛存在的，随着时间的积累，传感器噪声及故障信息经过积分环节会导致状态信息不可用，这也是解析余度应用于传感器容错的主要问题。传统的非线性卡尔曼滤波算法，如扩展卡尔曼滤波(EKF)、无迹卡尔曼滤波(UKF)等，可以实现噪声存在情况下飞行器的状态估计，但是当传感器故障存在的情况下，传统的非线性卡尔曼滤波算法的状态估计不准确，若故障幅值较大甚至导致状态信息不可用。

1967年，Friedland提出了二步卡尔曼滤波(TSKF)，这种滤波器针对常值偏差可以保证估计的最优性[1]。1993年，Alouani阐述了在随机偏差条件下二步卡尔曼滤波的无偏差滤波器的误差协方差矩阵满足某个代数条件限制的情况下，等价于增广状态卡尔曼滤波(ASKF)，即保证了状态估计的最优性，但该约束条件在实际系统往往是不成立的[2]。1999年，Hesieh和Chen提出了最优二步卡尔曼滤波(OTSKF)，去除了该约束条件，OTSKF在随机偏差存在情况下，仍然可以保证滤波器状态估计的最优性[3]。文献[4]应用了二步扩展卡尔曼滤波(TSEKF)实现了定常风场下的大气数据系统关键传感器的信号融合与重构，但文章中假设是定场风场，对于非定场风场情况，无法保证最优性。本文提出了最优二步无迹卡尔曼滤波(OTSUKF)，实现了非定场风场下飞行器的状态最优估计及惯性量测量传感器的故障辨识，并且以实际飞行数据进行了验证。

1 问题描述

IMU是飞行控制系统关键传感器，当IMU发生故障时，将会导致灾难性的后果。为了保证传感器数据的可靠性，工程中常为传感器采用硬件多余度配置，但硬件余度会使成本增加，负荷增加且容易发生共性故障等缺点。如何利用解析余度技术实现飞行器IMU的故障诊断是本文研究的问题。

2 滤波模型的建立

本文的研究对象是飞控系统关键传感器，利用卡尔曼滤波实现IMU的故障诊断。卡尔曼滤波基于解析余度，解析信号的精度取决于很大程度取决于模型的准确性。文献[5]给出了飞行器的力学方程：

(1)

式中，T表示发动机推力,m表示飞行器的质量,g表示重力加速度,u,v,w表示地速在机体系的投影,p,q,r表示飞行器运动的三轴角速率,φ,θ,ψ表示飞行器的姿态角,X,Y,Z是飞行器所受的气动力在飞行器机体系的投影,它的准确程度依赖于气动导数CX,CY,Cz的准确程度:

(2)

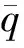
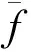
(3)

将公式(3)带入公式(1),得到修改后的飞行器力学方程:

(4)

文献[6]给出了飞行器的运动学方程:

(5)

考虑到加速度计和陀螺仪的测量噪声,可得到:

(6)

式中，axm,aym,azm是加速度计的测量值,pm,qm,rm是陀螺仪的测量值,fax,fay,faz是加速度计故障,fp,fq,fr是陀螺仪故障,ωax,ωay,ωaz是加速度计测量噪声,ωp,ωq,ωr是陀螺仪测量噪声。将公式(6)代入修改后的力学方程(4)和运动学方程(5),得到滤波器的系统方程:

(7)

三天线GNSS可以输出飞行器的速度和姿态信息[7],可得到滤波器的观测方程:

(8)

式中，uGSm,vGSm,wGSm是GNSS输出的导航坐标系的飞行器速度信息,φm,θm,ψm是GNSS输出的姿态信息,νu,νv,νw是GNSS输出速度信息的测量噪声,νφ,νθ,νψ是GNSS输出姿态信息的测量噪声,DCM是方向余弦矩阵,它建立起了机体系与导航系的坐标转换关系,它的定义为:

RDCM=

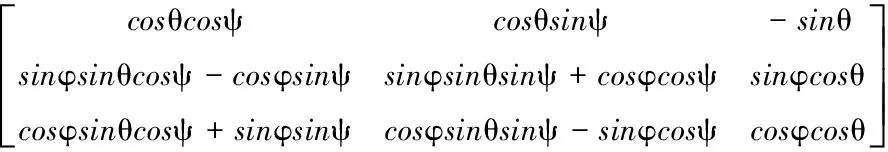
(9)

状态向量定义为:x=[uvwφθψ]T,观测向量定义为:y=[uGSmvGSmwGSmφmθmψm]T,输入向量定义为:u=[axmaxmaxmpmqmrm]T,IMU故障向量定义为:f=[faxfaxfaxfpfqfr]T。滤波模型可以简写成:

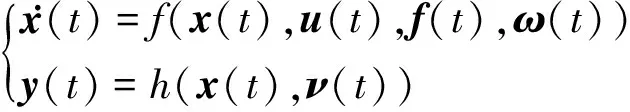
(10)

线性化和离散化方法可参照文献[4],经过线性化和离散化可以得到:

(11)

按照文献[4]提出可观测性检验方法,验证了(7)和(8)组成的滤波模型是可观测的,即可以通过观测来获得状态估计。故障建模成随机游走模型[8]:

(12)

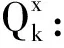
(13)

3 最优二步无迹卡尔曼滤波

3.1 无迹卡尔曼滤波基本原理

线性系统经过离散化处理,可以用以下离散系统描述:

(14)

针对上述系统,卡尔曼滤波的标准形式:

(15)

以上滤波算法确保了状态估计的最优性,但是系统(14)描述的是线性系统,而现实中的绝大多数系统都是非线性系统,例如本文所研究的飞行器是一个典型的复杂非线性系统,上述公式无法保证滤波结果的最优性。在文献[10]中,证明了:

(16)

利用sigma点经过非线性UT变换[11]来传递状态的均值和方差并利用以上等价形式进行迭代状态估计,是UKF的基本思想,并且文献[12]证明了噪声高斯分布情况下,UKF至少保证了状态估计达到EKF三阶截断的精度,而状态估计协方差矩阵也可以达到EKF二阶截断精度。UKF是一个比EKF性能更优秀的适用于复杂非线性系统的滤波算法。

3.2 二步卡尔曼滤波基本原理

本文研究的系统如(10)所示,经过离散化如(11)所示,由于故障f的存在,传统的卡尔曼滤波无法适用。传感器输出中,偏差是广泛存在且对精度影响最大的一种误差。二步卡尔曼滤波器的基本思想是设计一个无偏差影响的卡尔曼滤波器和一个偏差滤波器,并通过耦合矩阵V进行耦合实现最终的状态估计。此文中,将传感器故障f作为一种广义偏差进行研究,下文中将以故障替代偏差进行阐述。

1) 无故障滤波器基本原理:

本文将故障建模成了随机游走模型,考虑到故障的噪声对无故障滤波器的影响,对无故障滤波器的一步预测进行以下补偿:

(17)

(18)

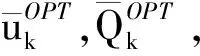
(19)

将作为故障滤波器的输入。

2) 故障滤波器基本原理:

文献[2]中推导了无故障滤波器的新息和增益及更新公式:

他的口气像是命令，但很诚恳。爱德华多愣愣地瞅了他一会儿，不知该怎么办。克里斯蒂安站起身，向爱德华多告了别，跨上马，不慌不忙地小跑着离去，他没有和胡利安娜打招呼，只把她当做一件物品。

(20)

通过上述公式,故障滤波器的输入即是无故障滤波器的新息,而Sk+1可以看成是故障滤波器的观测矩阵。值得注意的是,故障滤波器的输出即可以实现IMU的故障诊断。

3) 耦合矩阵计算与状态估计:

通过下述公式,矩阵V可以实现无故障滤波器的输出和故障滤波器的输出的耦合,实现飞行器状态估计:

(21)

3.3 最优二步无迹卡尔曼滤波基本原理

本文提出了适用于飞行器IMU故障诊断的最优二步无迹卡尔曼滤波算法,算法的具体流程如附录所示,滤波相关矩阵可以通过第二部分介绍的离散化过程获取。为了公式编排,做了以下简写:

(22)

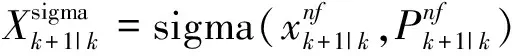
(23)

表示无故障滤波器滤波过程中的sigma点生成。

(24)

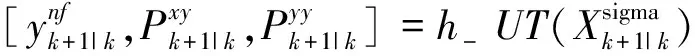
(25)

表示sigma点分别经过系统方程和观测方程的UT变换。sigma点生成和UT变换的具体算法实现可以参考文献[13]。

4 实际飞行数据验证与结果分析

4.1 实际飞行数据验证

由于数字仿真环境很难考虑到实际环境的外部因素干扰,本文采用荷兰代尔夫特理工大学提供的实际飞行数据(传感器无故障)进行验证。风速在机体系的投影如图1所示,本文所提出的最优二步无迹卡尔曼滤波方法在风场下仍可以实现飞控系统IMU的故障诊断,验证了所提出方法具有较强的鲁棒性。并与基于迭代最优二步扩展卡尔曼滤波(IOTSEKF)方法[14]进行了对比验证,说明本文提出的OTSUKF方法具有更加优越的性能。

MATLAB环境下,在10～20 s,25～35 s,40～50 s分别给加速度计和陀螺仪人为注入阶梯故障F1、斜坡故障F2和正弦故障F3 3种典型故障。

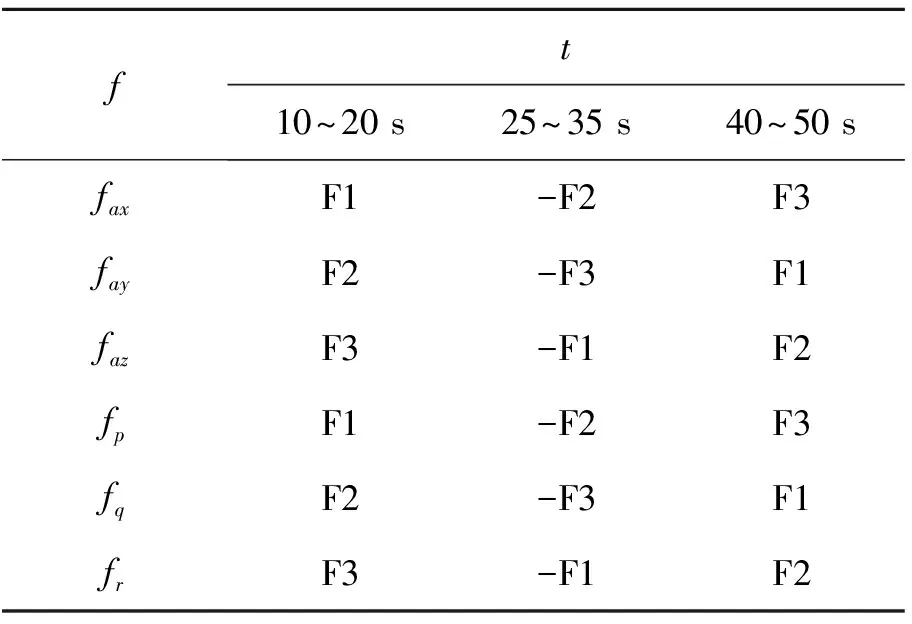
表1 加速度计和陀螺仪典型故障注入

其中故障的数学解析式为:

(26)

OTSUKF的初始化数据如公式(27)所示,其中q和R的特性由IMU和GNSS的误差特性决定:

(27)

状态与故障的实际值和OTSUKF的估计值如图2～5所示:

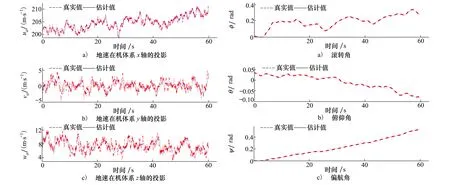
图1 地速在机体系的投影及IOTSEKF的估计值 图2 姿态角及IOTSEKF的估计值

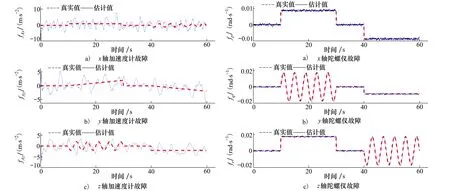
图3 加速度计故障及IOTSEKF的估计值 图4 陀螺仪故障及IOTSEKF的估计值

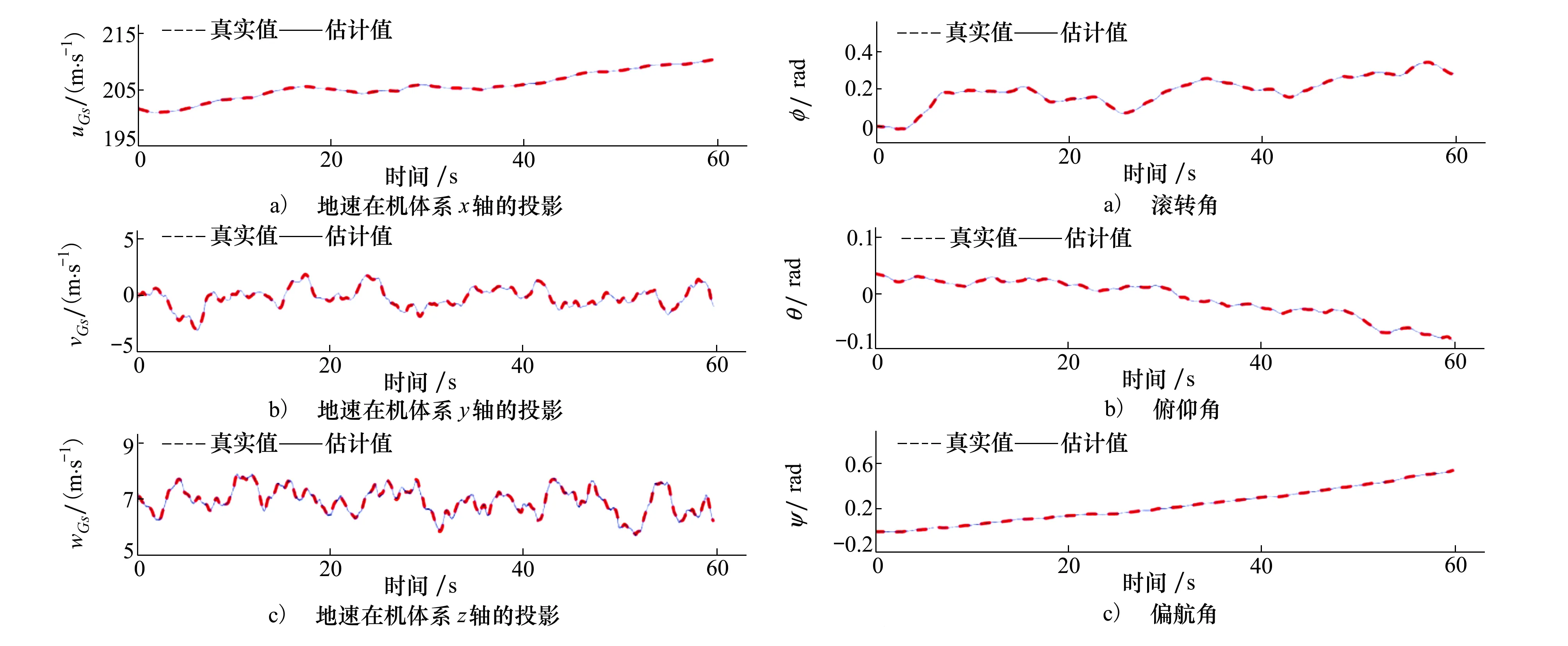
图5 地速在机体系的投影及OTSUKF的估计值 图6 姿态角及OTSUKF的估计值

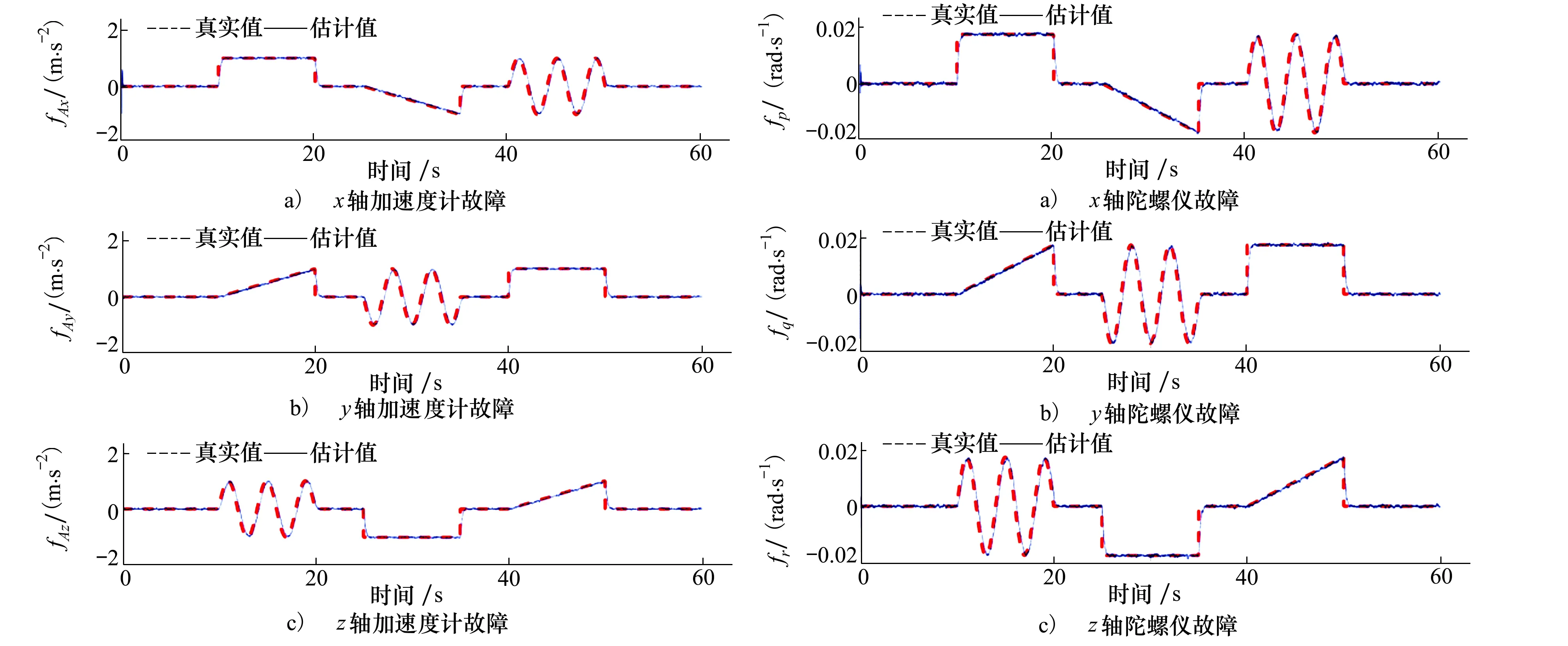
图7 加速度计故障及OTSUKF的估计值 图8 陀螺仪故障及OTSUKF的估计值

4.2 结果分析

基于IOTSEKF的IMU故障诊断方法所选取的滤波模型的系统方程与OTSUKF方法的系统方程一致,但是IOTSEKF的观测方程为:

(28)

式中，Vm,αm,βm是真空速、迎角和侧滑角传感器的测量值。IOTSEKF的滤波模型没有考虑风扰动的影响。实际飞行数据中记录的三轴风扰动uw,vw,ww信息如图9所示:

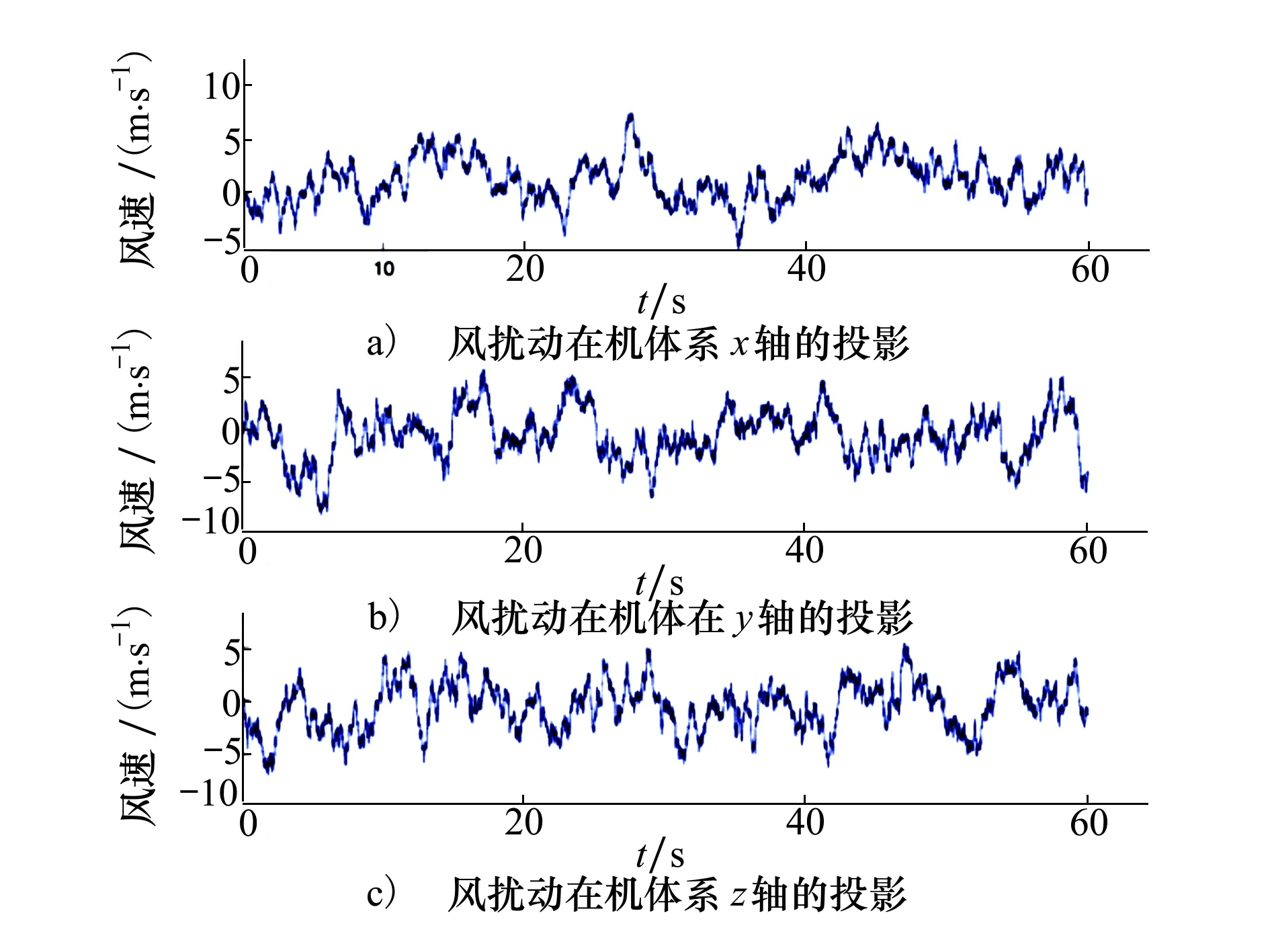
图9 风扰动在机体系的投影

风扰动存在情况下的观测方程的真实解析关系为:

(29)

风扰动的存在,IOTSEKF方法的滤波模型存在不确定性,这会导致滤波器状态估计性能的下降和故障诊断的不准确。本文修改观测方程如(8)式所示,它在风扰动情况下严格成立,进而使用OTSUKF进行最优状态估计与故障诊断。

对比图1与图5,不难发现对于飞行器三轴速度,OTSUKF较IOTSEKF的状态估计的准确度具有较大提升。对比图3与图7,不难发现对于三轴加速度计的故障诊断,OTSUKF较IOTSEKF的故障诊断的准确度具有较大提升。这也反映了OTSUKF方法对于风扰动具有鲁棒性,而IOTSUKF方法在风扰动出来情况下,状态估计和故障诊断效果较差。

由于风扰动主要影响前3个观测量,对于姿态角的估计和陀螺仪的故障诊断影响较小,很难分别从图2与图6的对比和图4与图8的对比得到OTSUKF较IOTSEKF的精确度提升。本文引入一项关于衡量估计准确度的指标,均方误差(root mean square error), 它的定义为:

(30)

对实际飞行数据验证的数据进行处理,得到RMSE如表2所示。分析表2的数据,可以发现风扰动下,OTSUKF较IOTSEKF对于三轴速度的估计的精度具有较大幅度提升;对于姿态角的估计精度提升不明显;对于加速度计故障诊断的精度具有较大幅度的提升;对于陀螺仪故障诊断的精度提升不明显。

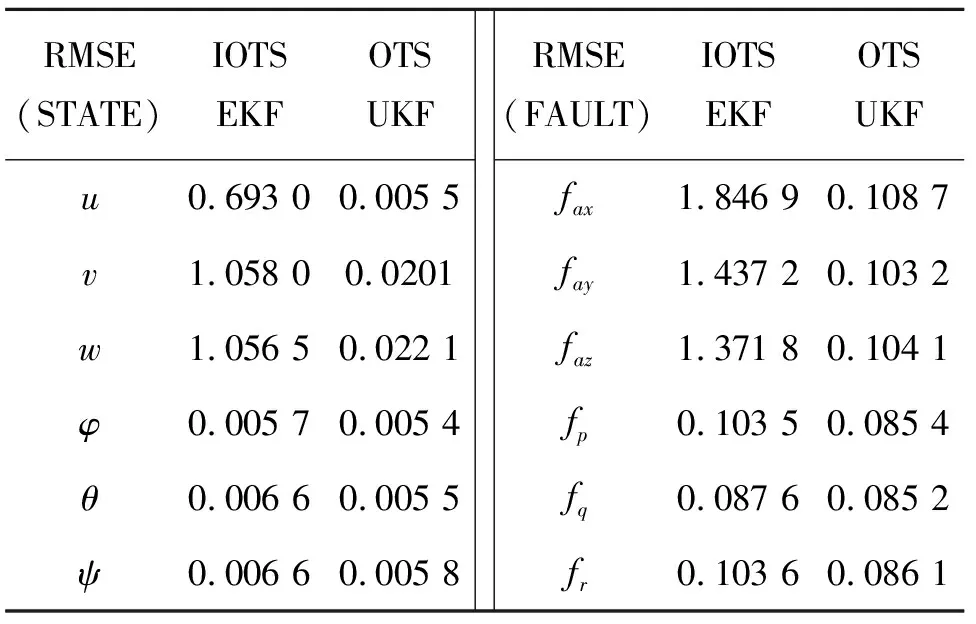
表2 状态估计与故障诊断的均方误差

5 结 论

本文将二步滤波思想与UKF滤波方法结合，提出了OTSUKF滤波方法。针对于飞行器，本文通过创新性的滤波模型设计，提出了一种适用于飞行器的滤波模型建立方法，并应用所提出的OTSUKF算法实现了飞飞行器三轴速度、姿态角的估计与IMU传感器故障的诊断。所以提出的OTSUKF方法经过了实际飞行数据验证其对风扰动具有鲁棒性并且与IOTSEKF方法进行了对比验证其最优性。所提出OTSUKF方法可以实现：

·对飞行器的速度与姿态信息进行估计。

·对IMU的多种变化类型的故障进行诊断。

·对风场具有鲁棒性，可以实际应用。